Skip to main content
SpringerLink
Log in

Modelling of the Discharge Coefficient of Differential Pressure Flowmeters by the Support Vector Machine

  • MECHANICAL MEASUREMENTS
  • Published:
Measurement Techniques Aims and scope

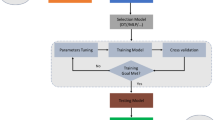
A study was performed of the problem of increasing the measurement precision of the flow rate of fluids and gases by differential-pressure flow meters. Modeling of the discharge coefficient of an orifice plate of differential-pressure flow meters by machine learning methods was examined. It was shown that existing models of the discharge coefficient of an orifice plate are complex, and the values of the coefficients must be made more precise in the process of flow meter use. It is proposed to use, for the discharge coefficient of an orifice plate, a model based on a support vector machine. The structure and training process of the model are described, and the training parameters are specified. The modeling results obtained in training and testing the model are given, and its effectiveness was confirmed. A comparative analysis was performed of the proposed model based on a support vector machine and the existing model in the form of the Reader- Harris–Gallagher empirical equation. It is shown that the proposed model of the discharge coefficient is not inferior to the precision and effectiveness of the working model, and this makes it possible to improve systems for measuring the flow rate of fluids and gases. The results of the study will be useful for operations in the fields of production, transport, and storage of natural gas.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

References

  1. J. Yoder, “Measuring a 1% obtain in a 4.5 billion dollars market”, FlowControl, 6, 42–45 (2008).

    Google Scholar 

  2. Zh. A. Daev, “Comparative analysis of the discharge coefficients of flow meters with variable pressure drop,” Metrologiya, No. 1, 32–36 (2015).

  3. M. Reader-Harris, Orifice Plates and Venturi Tubes, Springer Switzerland, Glasgow (2015), https://doi.org/10.1007/978-3-319-16880-7.

  4. D. E. Cristancho, K. R. Hall, L. A. Coy, and G. A. Iglesias-Silva, Flow Measur. Instrum., 21, No. 3, 299–301 (2010), https://doi.org/10.1016/j.flowmeasinst.2010.03.003.

    Article  Google Scholar 

  5. J. A. Stolz, “Universal equation for the calculation of discharge coefficient of orifice plates,” in Proc. FLOMEKO 1978. IMEKO-Conference on Flow Measurement of Fluids, Groningen, Netherlands, Sept. 11–15, 1978, North-Holland, Amsterdam (1978), pp. 519–534.

  6. M. J. Reader-Harris and J. A. Sattary, Flow Measus. Instrum., 1, No. 2, 67–76 (1990), https://doi.org/10.1016/0955-5986(90)90031-2.

    Article  Google Scholar 

  7. M. J. Reader-Harris, J. A. Sattary, and E. R. Spearman, The Orifice Plate Discharge Coefficient Equation, Progress Report No. PR14. EUEC/17 (EEC005), National Engineering Laboratory Executive Agency, East Kilbride, Glasgow (1992).

  8. M. J. Reader-Harris, J. A. Sattary, and E. R. Spearman, Flow Measur. Instrum., 6. No. 2, 101–114 (1995), https://doi.org/10.1016/0955-5986(94)00001-0.

    Article  Google Scholar 

  9. M. J. Reader-Harris, C. Forsyth C., and T. Boussouara, Flow Measur. Instrum., 82, 102043 (2021), https://doi.org/10.1016/j.flowmeasinst.2021.102043.

  10. E. N. Ahmed and A. A. Ghanem, Flow Measur. Instrum., 73. 101751 (2020), https://doi.org/10.1016/j.flowmeasinst.2020.101751.

    Article  Google Scholar 

  11. C. L. Hollingshead, M. C. Johnson, S. L. Barfuss, and R. E. Spall, J. Petrol. Sci. Eng., 78, No. 3–4, 559–566 (2011), https://doi.org/10.1016/j.petrol.2011.08.008.

    Article  Google Scholar 

  12. Zh. A. Dayev, Flow Measur. Instrum., 71, 101674 (2020), https://doi.org/10.1016/j.flowmeasinst.2019.101674.

    Article  Google Scholar 

  13. Zh. Dayev and A. K. Kairakbaev, Appl. Artif. Intell., 35, 1128–1146 (2021), https://doi.org/10.1080/08839514.2021.1975378.

    Article  Google Scholar 

  14. Zh. Dayev, A. Kairakbaev, K. Yetilmezsoy, et al., Flow Measur. Instrum., 79, 101913 (2021), https://doi.org/10.1016/j.flowmeasinst.2021.101913 (2021).

  15. Zh. A. Dayev and L. N. Latyshev, Flow Measur. Instrum., 56, 18–22 (2017), https://doi.org/10.1016/j.flowmeasinst.2017.07.001.

    Article  Google Scholar 

  16. S. Haykin, Neural Networks, A Comprehensive Foundation, Prentice Hall (1999).

  17. J. G. Jarushkina, Foundations of Imprecise and Hybrid Systems, Finansy i Statistika, Moscow (2009).

    Google Scholar 

  18. D. Borg, M. Suetake, and D. Brandao, Flow Measur. Instrum., 40, 142–148 (2014), https://doi.org/10.1016/j.flowmeasinst.2014.09.007

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Baishev University, Aktobe, Republic of Kazakhstan

    Zh. A. Dayev & G. E. Shopanova

Authors
  1. Zh. A. Dayev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. E. Shopanova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. E. Shopanova.

Additional information

Translated from Izmeritel’naya Tekhnika, No. 4, pp. 37–42, April, 2022.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dayev, Z.A., Shopanova, G.E. Modelling of the Discharge Coefficient of Differential Pressure Flowmeters by the Support Vector Machine. Meas Tech 65, 266–272 (2022). https://doi.org/10.1007/s11018-022-02078-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11018-022-02078-5

Keywords

Search

Navigation