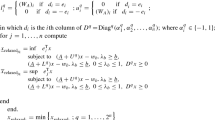Skip to main content
SpringerLink
Log in

Combined Method for the Correction of Interval Systems of Linear Algebraic Equations

  • Published:
Measurement Techniques Aims and scope

This article discusses the application of an interval approach in solving problems in the field of physics, particularly spectral analysis. To process data with interval uncertainty, a linear interval tolerance problem is modeled, and the inconsistency (unsolvability) of an interval system of linear algebraic equations (ISLAE) with the use of a recognizing functional is presented. The actual regularization problem of the inconsistent interval systems of linear equations is solved. The idea of a combined method for correcting a linear interval tolerance problem, formulated by S. Shary, is implemented. A new method for controlling the solution of an ISLAE was developed by changing the radii of the matrix elements of the system. The research results can be used, for example, to calculate the concentrations of substances through the measurement of characteristic x-ray radiation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

References

  1. A. N. Bazhenov and P. A. Zatylkin, “Application of the interval approach for spectral analysis. Investigation of the solvability of a problem using a recognizing functional,” Izmer. Tekhn., No. 2, 6–12 (2019), https://doi.org/10.32446/0368-1025it.2019-2-6-12.

  2. A. N. Bazhenov and P. A. Zatylkin, “Small angle reconstruction of plasma luminosity for a spherical tokamak,” Vychisl. Tekhnol., 25, No. 1, 5–38 (2020), https://doi.org/10.25743/ICT.2020.25.1.002.

    Article  Google Scholar 

  3. S. P. Shary, Finite-Dimensional Interval Analysis, XYZ, Novosibirsk (2021), www.nsc.ru/interval/Library/InteBooks/SharyBook.pdf, acc. 06.16.2021.

  4. B. Kirfott, M. Nakao, A. Neumeier, et al., “Standardization of notation in interval analysis,” Vychisl. Tekhnol., 15, No. 1, 7–13 (2010).

    Google Scholar 

  5. A. N. Bazhenov, Interval Analysis. Fundamentals of Theory and Teaching Examples: Teach. Aid, SPbPU, St. Petersburg (2020), https://doi.org/10.18720/SPBPU/2/s20-76.

  6. O. Kosheleva, S. P. Shary, Gang Xiang, and R. Zapatrin (eds.), Beyond Traditional Probabilistic Data Processing Techniques: Interval, Fuzzy etc. Methods and Their Applications, Springer Cham (2020), https://doi.org/10.1007/978-3-030-31041-7.

  7. x-Ray Data Booklet Table 1-3, http://xdb.lbl.gov/Section1/Table_1-3.pdf, acc. 06.16.2021.

  8. S. P. Shary, “Solution of the interval linear tolerance problem,” Avtomat. Telemekh., No. 10, 147–162 (2004).

  9. S. P. Shary and I. A. Sharaya, “Recognition of the solvability of interval equations and its applications to data analysis,” Vychisl. Tekhnol., 18, No. 3, 80–109 (2013).

    Google Scholar 

  10. S. P. Shary, “The problem of recovering dependencies from data with interval uncertainty,” Zavod. Lab. Diagn. Mater., 86, No. 1, 62–74 (2020).

    Article  Google Scholar 

  11. N. Z. Shor and P. I. Stetsyuk, “Using a modification algorithm to determine the global minimum of polynomial functions,” Kibern. Sist. Analiz, No. 4, 28–49 (1997).

  12. P. I. Stetsyuk, “Subgradient methods ralgb5 and ralgb4 for minimizing ravine convex functions,” Vychisl. Tekhnol., 22, No. 2, 127–149 (2017).

    Google Scholar 

  13. M. L. Smolsky, Solving the Interval Linear Tolerance Problem by the Method of Recognizing Functional: Bachelor’s Final Qualification Work, SPbPU (2020), https://doi.org/10.18720/SPBPU/3/2020/vr/vr20-1397.

  14. S. I. Zhilin, Reliab. Comput., 11, 433–442 (2005), https://doi.org/10.1007/s11155-005-0050-3.

    Article  MathSciNet  Google Scholar 

  15. S. P. Shary, Math. Comput. Simul., 39, No. 1–2, 53–85 (1995), https://doi.org/10.1016/0378-4754(95)00135-K.

    Article  Google Scholar 

  16. S. P. Shary and I. A. Sharaya, “Reserve of characteristic inclusion for interval linear systems of relations,” Vychisl. Tekhnol., 26, No. 3, 61–85 (2021), https://doi.org/10.25743/ICT.2021.26.3.005.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Peter the Great St. Petersburg Polytechnic University, St. Petersburg, Russia

    A. N. Bazhenov

  2. Ioffe Institute, St. Peterburg, Russia

    A. N. Bazhenov & A. Yu. Telnova

Authors
  1. A. N. Bazhenov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Yu. Telnova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. N. Bazhenov.

Additional information

Translated from Metrologiya, No. 4, pp. 17–39, October–December, 2021.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bazhenov, A.N., Telnova, A.Y. Combined Method for the Correction of Interval Systems of Linear Algebraic Equations. Meas Tech 64, 969–977 (2022). https://doi.org/10.1007/s11018-022-02031-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11018-022-02031-6

Keywords

Search

Navigation