Skip to main content
SpringerLink
Log in

Estimating the Integral of the Square of Derivatives of Symmetric Probability Densities of One-Dimensional Random Variables

  • Published:
Measurement Techniques Aims and scope

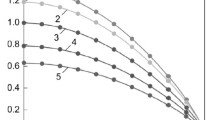
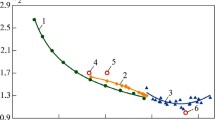
In justifying a method for rapid choice of the spread coefficient of kernel probability density estimates, a constant has been found which is a functional of the second derivative of the density. This result is generalized to the derivatives of symmetric probability densities of different orders in this paper. Functional dependences of these constants on the coefficient of antikurtosis of a random variable are found. The features of these constants are studied. A method for estimating functionals of derivatives of the probability densities that assumes fulfillment of the following steps is developed on the basis of these results. The mean square deviation of the one-dimensional random variables and the antikurtosis coefficient are estimated from the original sample. The recovered functional dependences of the antikurtosis are used to estimate the values of constants which are functionals of the derivatives of the probability density. For the known estimates of the mean square deviation of random variable being studied and the constant examined here, the values of the functional of the derivative of the probability distribution of the chosen order are calculated. The results are confirmed by analyzing data from a numerical simulation. It is found that with increasing order of the derivative, the estimates of these functionals increase. This fact is explained by the increasing complexity of the integrand in these functionals. The proposed method provides objective results for the first three derivatives of the probability density of the random variable. The results of this study are confirmed by a confidence estimate for the functionals studied here.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. E. Parzen, Ann. Math. Stat., 33, No. 3, 1065–1076 (1962).

    Article  Google Scholar 

  2. V. A. Epanechnikov, “Non-parametric estimation of a multivariate probability density,” Teor. Veroyatn. Primen., 14, No. 1, 156–161 (1969).

    MathSciNet  MATH  Google Scholar 

  3. A. V. Lapko and V. A. Lapko, “Fast algorithm for choice of spread coefficients of kernel functions in nonparametric estimates of probability density,” Izmer. Tekhn., No. 6, 16–20 (2018), https://doi.org/10.32446/0368-1025it-2018-6-16-20.

  4. D. W. Scott, Multivariate Density Estimation: Theory, Practice, and Visualization, John Wiley & Sons, New Jersey (2015).

    Book  Google Scholar 

  5. A. V. Lapko and V. A. Lapko, “Relationship between parameters of histograms and kernel estimates of single-mode probability densities,” Izmer. Tekhn., No. 9, 3–8 (2019), https://doi.org/10.32446/0368-1025it.2019-9-3-8.

  6. A. V. Lapko and V. A. Lapko, “Relationship between parameters of histograms and kernel estimates of the probability density of a univariate random variable,” Izmer. Tekhn., No. 11, 18–23 (2019), https://doi.org/10.32446/0368-1025it.2019-11-18-23.

  7. A. V. Lapko and V. A. Lapko, “Fast algorithm for choosing spread coefficients in multidimensional kernel estimates of probability density,” Izmer. Tekhn., No. 10, 19–23 (2019), https://doi.org/10.32446/0368-1025it.2018-10-19-23.

  8. A. V. Lapko and V. A. Lapko, “Method for fast selection of spread coefficients of kernel functions in a nonparametric algorithm for sample identification,” Izmer. Tekhn., No. 4, 4–8 (2019), https://doi.org/10.32446/0368-1025it.2019-4-4-8.

  9. A. V. Lapko and V. A. Lapko, “Choice of spread coefficients for kernel estimates of probability density under large sample conditions,” Izmer. Tekhn., No. 5, 3–6 (2019), https://doi.org/10.32446/0368-1025it.2019-5-3-6.

  10. V. C. Raykar and R. Duraiswami, “Fast optimal bandwidth selection for kernel density estimation,” 6th SIAM Int. Conf. on Data Mining (2006), pp. 522–526.

  11. C. Rohlfs and M. Zahran, “Optimal bandwidth selection for kernel regression using a fast grid search and a GPU,” in: 2017 IEEE Int. Parallel and Distributed Processing Symposium Workshops (IPDPSW) (2017), pp. 550–556, https://doi.org/10.1109/IPDPSW.2017.130.

  12. B. W. Silverman, J. Royal Stat. Soc., Ser. C, Appl. Stat., 31, No. 1, 93–99 (1982).

  13. S. Sheather and M. Jones, J. Royal Stat. Soc., Ser. B, 53, No. 3, 683–690 (1991).

Download references

Author information

Authors and Affiliations

  1. Institute of Computational Modeling, Siberian Branch of the Russian Academy of Sciences (ICM SB RAS), Krasnoyarsk, Russia

    A. V. Lapko & V. A. Lapko

  2. Reshetnev Siberian State University of Science and Technology, Krasnoyarsk, Russia

    A. V. Lapko & V. A. Lapko

Authors
  1. A. V. Lapko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. A. Lapko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. V. Lapko.

Additional information

Translated from Metrologiya, No. 1, pp. 15–27, January–March, 2020.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lapko, A.V., Lapko, V.A. Estimating the Integral of the Square of Derivatives of Symmetric Probability Densities of One-Dimensional Random Variables. Meas Tech 63, 171–176 (2020). https://doi.org/10.1007/s11018-020-01768-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11018-020-01768-2

Keywords

Search

Navigation