Skip to main content
SpringerLink
Log in

Stochastic Estimation of Orientation Parameters of an Antenna Complex based on Strapdown Inertial System Measurements

  • GENERAL PROBLEMS OF METROLOGY AND MEASUREMENT TECHNIQUE
  • Published:
Measurement Techniques Aims and scope

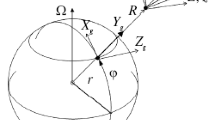
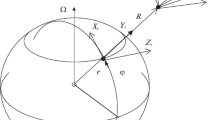
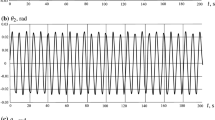
The problem of high-precision determination of the spatial orientation of the antennas of radio complexes located on high-rise masts of various designs is considered. It is established that the methods currently used, based on measurements of satellite navigation systems and autonomous measurements of strapdown inertial orientation systems, do not provide the required accuracy in solving the problem. It is shown that the low accuracy of existing methods is due to both weak noise immunity of information processing algorithms and the lack of the ability to take into account the dynamic properties of orientation parameters measured under conditions of high intensity interference, the properties of which, as a rule, are not taken into account. A dynamic algorithm is proposed for estimating the stochastic orientation parameters of the antenna of a radio complex, which is invariant to the nature of the movement of the mast base and provides stability and the required estimation accuracy under general assumptions about the nature of the interference of the sensitive elements of the strapdown inertial orientation system. The Rodrigue–Hamilton parameter vector was used as the observed state vector – the antenna orientation parameter vector – and the vector of measurements of the angular velocity sensors of the strapdown inertial system was used as the observation vector for it. The instrumentation of the strapdown inertial system includes three accelerometers and three angular velocity sensors located orthogonally at the center of mass of the antenna. Based on the obtained non-linear stochastic equations for the dynamics of the change in the parameter vector of the current orientation of the strapdown inertial orientation system on a moving base and the equations of their observation, a stochastic model of measurement signals for sensitive elements of the strapdown inertial orientation system, a non-linear (generalized) Kalman filter is constructed that provides the desired solution to the problem of estimating the parameters of the current antenna orientation on a perturbed base. We present the results of a numerical experiment and a conclusion about the possibility of using a fi lter to solve the problem of operational orientation of antennas of radio engineering complexes using medium- and high-precision strapdown inertial orientation systems and without correction over a long time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.

Similar content being viewed by others

References

  1. D. Dardari, E. Falletti, and M. Louise (eds.), Satellite and Terrestrial Radio Positioning Techniques. A Signal Processing Persective [Russian translation], Technosphere, Moscow (2012).

  2. D. V. Zaitsev, Multiposition Radar Systems. Methods and Algorithms for Processing Information under Interference, Radiotekhnika, Moscow (2007).

    Google Scholar 

  3. A. A. Konovalov, Fundamentals of Trajectory Processing of Radar Information, Izd. LETI, St. Petersburg (2013).

    Google Scholar 

  4. M. N. Krasilshchikov and G. G. Sebryakov (eds.), Modern Information Technologies in the Problems of Navigation and Guidance of Unmanned Maneuverable Aircraft, Fizmatlit, Moscow (2009).

    Google Scholar 

  5. S. V. Sokolov, V. A. Pogorelov, and A. B. Shatalov, “Solution of the problem of autonomous initial orientation of BINS in a perturbed setting using the Rodrigue–Hamilton parameters,” Izv. Vuzov. Aviats. Tekhn., No. 1, 4–12 (2019).

    Google Scholar 

  6. S. V. Sokolov and V. A. Pogorelov, “Non-linear dynamic estimation of the orientation angles of a moving object from distributed satellite measurements,” Izmer. Tekhn., No. 4, 30–36 (2019), DOI: https://doi.org/10.32446/0368-1025it.2019-3-30-36.

  7. I. Kinkulkin, Global Navigation Satellite Systems. Algorithms for the Functioning of Consumption Equipment: Monograph, Radiotekhnika, Moscow (2018), DOI: 10.18127.B9785931081755.

  8. I. N. Rosenberg, S. V. Sokolov, V. I. Umansky, and V. A. Pogorelov, Theoretical Foundations of Close Integration of Inertial-Satellite Navigation Systems, Fizmatlit, Moscow (2018).

    Google Scholar 

  9. S. V. Sokolov and V. A. Pogorelov, Stochastic Estimation, Control and Identifi cation in High-Precision Navigation Systems, Fizmatlit, Moscow (2016).

    Google Scholar 

  10. S. V. Sokolov and V. A. Pogorelov, Fundamentals of the Synthesis of Multi-Structured Strapdown Navigation Systems, Fizmatlit, Moscow (2009).

    Google Scholar 

  11. G. I. Emelyantsev and A. P. Stepanov, Integrated Inertial-Satellite Orientation and Navigation Systems, V. G. Peshekhonov (ed.), TsNII Elektropribor, St. Petersburg (2016).

  12. E. Vaknin and I. Klein I., Gyrosc. Navig., 7, No. 2, 145–151 (2016), DOI: https://doi.org/10.1134/S2075108716020115.

  13. T. Brunner, S. Changey, E. Pecheur, et al., “Evaluation of attitude estimation algorithms using absolute magnetic reference data: Methodology and results,” Proc. of the Position, Location and Navigation Symp., PLANS 2014, Monterey, USA, May 5–8, 2014, pp. 212–218, DOI: https://doi.org/10.1109/PLANS.2014.6851378.

  14. V. I. Lukasevich, V. A. Pogorelov, and S. V. Sokolov, “Algorithm for estimating the rotation parameters of a distributed antenna from satellite measurements,” Radiotekhn. No 6, 122–132 (2015).

    Google Scholar 

  15. S. V. Sokolov, V. A. Pogorelov, and V. I. Lukasevich, “Non-linear stochastic fi ltering of the parameters of the angular motion of a distributed antenna by satellite measurements,” Datch. Systemy, No 5, 8–17 (2015).

  16. J. Blanch, T. Walter, and P. Enge, Proc. IEEE, Spec. Centen. Iss., 13, 1821–830 (2012), DOI: https://doi.org/10.1109/JPROC.2012. 2190154.

  17. E. Ezzaldeen, S. Knedlik, and O. Loffeld, Sensors, 12.5, 5310–5327 (2012), DOI: https://doi.org/10.3390/s120505310.

    Article  Google Scholar 

  18. A. J. Jahromi, A. Broumandan, J. Nielsen, and G. Lachapelle, Int. J. Navig. Observ., 2012, Art. ID127072, 1–16 (2012), DOI: https://doi.org/10.1155/2012/127 072.

  19. A. R. Baziar, M. Moazedi, and M. R. Mosavi, J. Wireless Pers. Commun., 83, No. 3, 1955–1970 (2015), DOI: 10. 1007/s11277-015-2497-9.

  20. J. Bhatti and T. E. Humphreys, J. Inst. Navig., 4, No. 1, 51–66 (2017), DOI: https://doi.org/10.1002/navi.183.

    Article  Google Scholar 

  21. M. L. Psiaki, B. W. O’Hanlon, S. P. Powell, and J. A. Bhatti, GPS World, 25, No. 11, 36–44 (2014).

    Google Scholar 

  22. O. S. Salychev, Verifi ed Approaches to Inertial Navigation, BMSTU Press Publ., Moscow (2017).

    Google Scholar 

  23. O. S. Salychev, Applied Inertial Navigation: Problems and Solutions, BMSTU Press Publ., Moscow (2004).

    Google Scholar 

  24. V. V. Matveev and V. Ya. Raspopov, Instruments and Systems of Orientation, Stabilization, and Navigation on MEMS Sensors, Izd. TulaSU, Tula (2017).

  25. Yu. N. Chelnokov, Quaternion Models and Methods of Dynamics, Navigation, and Motion Control, Fizmatlit, Moscow (2011).

    Google Scholar 

  26. I. N. Sinitsyn, Kalman and Pugachev Filters, Logos, Moscow (2006).

    Google Scholar 

  27. S. V. Sokolov, S. M. Kovalev, P. A. Kucherenko, and Yu. A. Smirnov, Methods for Identifying Fuzzy and Stochastic Systems, Fizmatlit, Moscow (2018).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Innovative Engineering Technologies, Peoples’ Friendship University of Russia (RUDN), Moscow, Russia

    S. V. Sokolov & V. A. Pogorelov

  2. Serpukhov Metallist Plant, Serpukhov, Moscow Region, Russia

    A. B. Shatalov

Authors
  1. S. V. Sokolov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. A. Pogorelov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. B. Shatalov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to S. V. Sokolov or A. B. Shatalov.

Additional information

Translated from Izmeritel’naya Tekhnika, No. 2, pp. 11–19, February, 2020.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sokolov, S.V., Pogorelov, V.A. & Shatalov, A.B. Stochastic Estimation of Orientation Parameters of an Antenna Complex based on Strapdown Inertial System Measurements. Meas Tech 63, 87–95 (2020). https://doi.org/10.1007/s11018-020-01755-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11018-020-01755-7

Keywords

Search

Navigation