Exact solution to axisymmetric interface crack problem in piezo-electric transversely isotropic materials

Abstract

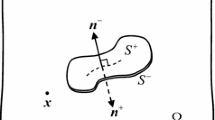
This seems to be the first exact closed form solution to the problem of a penny-shaped interface crack, subjected to an axisymmetric normal and tangential loading. The crack is located at the boundary between two bonded piezo-electric transversely isotropic half-spaces, made of different materials. We use the combination of Green’s functions for 2 different half-spaces and Fourier transform. We derive first the governing equations, which are valid for a crack of arbitrary shape. The usual approach leads to 4 hypersingular integral equations, we arrive at 3 integro-differential equations (one of them being complex). While the coefficients of the governing equations in existing publications are presented in terms of the results of the solution of a set of linear algebraic equations and are too cumbersome to be written explicitly in terms of the basic constants, our choice of the basic constants leads to quite elegant explicit expressions for these coefficients and reveals certain symmetry, which was noticed only numerically in previous publications or not noticed at all. In the particular case of axial symmetry, the problem is reduced to just one singular equation, for which exact closed form solution is known. We are not aware of any other publication with which our results can be compared.

Appendix 1

We present below the table of Fourier integral transforms, used in this article.

$$\begin{aligned}{} & {} \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }{1\over \sqrt{\xi ^{2}_{1}+\xi ^{2}_{2}}} \exp (-\zeta z)\nonumber \\{} & {} \quad \exp [-i(x\xi _{1}+y\xi _{2})]d\xi _{1}d\xi _{2} = {2\pi \over R_{0}}, \end{aligned}$$

(135)

$$\begin{aligned}{} & {} \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }{i\xi _{2}\over (\xi ^{2}_{1}+\xi ^{2}_{2})} \exp (-\zeta z)\nonumber \\{} & {} \quad \exp [-i(x\xi _{1}+y\xi _{2})]d\xi _{1}d\xi _{2} = {2\pi y\over R_{0}(R_{0}+z_{g})}, \end{aligned}$$

(136)

$$\begin{aligned}{} & {} \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }{i\xi _{1}\over (\xi ^{2}_{1}+\xi ^{2}_{2})} \exp (-\zeta z)\nonumber \\{} & {} \quad \exp [-i(x\xi _{1}+y\xi _{2})]d\xi _{1}d\xi _{2} = {2\pi x\over R_{0}(R_{0}+z_{g})}, \end{aligned}$$

(137)

$$\begin{aligned}{} & {} \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }{\xi ^{2}_{1}\over (\xi ^{2}_{1}+\xi ^{2}_{2})^{3/2}} \exp (-\zeta z)\nonumber \\{} & {} \quad \exp [-i(x\xi _{1}+y\xi _{2})]d\xi _{1}d\xi _{2} = \pi \Bigg [{1\over R_{0}} + {y^{2}-x^{2}\over R_{0}(R_{0}+z_{g})^{2}}\Bigg ], \end{aligned}$$

(138)

$$\begin{aligned}{} & {} \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }{\xi ^{2}_{2}\over (\xi ^{2}_{1}+\xi ^{2}_{2})^{3/2}} \exp (-\zeta z)\nonumber \\{} & {} \quad \exp [-i(x\xi _{1}+y\xi _{2})]d\xi _{1}d\xi _{2} = \pi \Bigg [{1\over R_{0}} - {y^{2}-x^{2}\over R_{0}(R_{0}+z_{g})^{2}}\Bigg ], \end{aligned}$$

(139)

$$\begin{aligned}{} & {} \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }{\xi _{1}\xi _{2}\over (\xi ^{2}_{1}+\xi ^{2}_{2})^{3/2}} \exp (-\zeta z)\nonumber \\{} & {} \quad \exp [-i(x\xi _{1}+y\xi _{2})]d\xi _{1}d\xi _{2} = - {2\pi xy\over R_{0}(R_{0}+z_{g})^{2}}, \end{aligned}$$

(140)

The following notation was introduced in the formulas above:

$$\begin{aligned} \zeta = {1\over \gamma } \sqrt{\xi ^{2}_{1}+\xi ^{2}_{2}},\qquad R_{0} = \sqrt{z^{2}_{g}+x^{2}+y^{2}},\qquad z_{g} = {z\over \gamma }. \end{aligned}$$

(141)