Skip to main content
SpringerLink
Log in

Calculation of the strength of spirally organized cellulose fibers using the generalized Euler-Eitelwein formula

  • Published:
Meccanica Aims and scope Submit manuscript

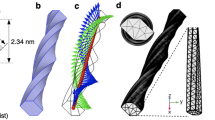
Abstract

A theoretical model has been proposed to investigate the strength of helical coupling of nanocellulose into nanofibrils and nanofibrils into microfibrils. Namely, the force held by an elastic rod uniformly wrapped around a cylinder in a helix with a finite step was calculated. The initial shape of the elastic rod in the unstressed state was assumed to be helical (rather than rectilinear). The bending stiffness of the rod was taken into account. We have also taken into account the Coulomb friction and adhesion of the rod to the cylinder, which prevents slippage, and their attraction, which prevents detachment. Our result generalizes the Euler–Eitelwein formula for winding a thread normal to the generatrix of a rough cylinder in the absence of thread bending stiffness and attraction to the cylinder. We found that the spatial nature of the winding significantly reduces the strength of the helical connection, but it is still much stronger than a non-helical connection.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Hanley S, Revol J, Godbout L, Gray D (1997) Atomic force microscopy and transmission electron microscopy of cellulose from Micrasterias denticulata; evidence for a chiral helical microfibril twist. Cellulose 4:209–220

    Article  Google Scholar 

  2. Zhao Z, Shklyaev O, Nili A, Mohamed M, Kubicki J, Crespi V, Zhong L (2013) Cellulose microfibril twist, mechanics, and implication for cellulose biosynthesis. J Phys Chem A 117:2580–2589

    Article  Google Scholar 

  3. Nikolsky SN, Zlenko DV, Melnikov VP, Stovbun SV (2019) The fibrils untwisting limits the rate of cellulose nitration process. Carbohyd Polym 204:232–237

    Article  Google Scholar 

  4. Usachev SV, Zlenkoa DV, Nagornova IV, Koverzanova EV, Mikhaleva MG, Vedenkin AS, Vtyurina DN, Skoblin AA, Nikolsky SN, Politenkova GG, Stovbun SV (2020) Structure and properties of helical fibers spun from cellulose solutions in [Bmim]Cl. Carbohyd Polym 235:115866

    Article  Google Scholar 

  5. Stovbun SV, Nikol’skii SN, Mel’nikov VP, Mikhaleva MG, Litvin YA, Shchegolikhin AN, Zlenko DV, Tverdislov VA, Gerasimov DS, Rogozin AD (2016) Chemical physics of cellulose nitration. Rus J Phys Chem B 10(2):245–259. https://doi.org/10.1134/S199079311602024X

    Article  Google Scholar 

  6. Zlenko DV, Vtyurina DN, Usachev SV, Skoblin AA, Mikhaleva MG, Politenkova GG, Nikolsky SN, Stovbun SV (2021) On the orientation of the chains in the mercerized cellulose. Scientifc Reports 11:8765

    Article  Google Scholar 

  7. Buchanan B, Gruissem W, Jones R (2015) Biochemistry and molecular biology of plants, 2nd Edition. Chichester, West Sussex. 1264 pages c.—ISBN 9780470714225

  8. Zlenko DV, Nikolsky SN, Vedenkin AS, Politenkova GG, Skoblin AA, Melnikov VP, Mikhaleva MG, Stovbun SV (2019) Twisting of fibers balancing the gel-sol transition in cellulose aqueous suspensions. Polymers 11:873. https://doi.org/10.3390/polym11050873

    Article  Google Scholar 

  9. Popov VL (2016) Kontaktmechanik und Reibung. 3. Auflage, Springer, ISBN 978–3–662–45974–4, Seite 169 ff; C. Spura: Technische Mechanik 1. Stereostatik. Springer, ISBN 978–3–658–14984–0

  10. Weber MO, Ehrmann A (2012) Necessary modification of the Euler-Eytelwein formula for knitting machines. J Text Inst. https://doi.org/10.1080/00405000.2011.598665

    Article  Google Scholar 

  11. Stovbun SV, Skoblin AA, Zlenko DV (2018) Self assembly and gelation in solutions of chiral N-trifluoroacetylated α-aminoalcohols. Chem Phys 508:34–44

    Article  Google Scholar 

  12. Landau LD, Lifshitz EM (1986) Theory of elasticity. Vol. 7 (3rd ed.). Butterworth-Heinemann. p. 195 ISBN 978–0–7506–2633–0

  13. Antman SS (2005) Nonlinear problems of elasticity, 2nd edn. Springer, NY

    MATH  Google Scholar 

  14. Goriely A (2017) The mathematics and mechanics of biological growth. Springer, NY

    Book  Google Scholar 

  15. Konyukhov A and Schweizerhof K (2013) Frictional interaction of a spiral rope and a cylinder – 3D-generalization of the Euler-Eytelwein formula considering pitch. https://doi.org/10.1007/978-3-642-31531-2_14.

  16. Kreyszig E (1991) Differential geometry. Dover Publications, New York ISBN 0-486-66721-9

  17. Chichibabin AE (1963) Fundamental principles of organic chemistry [in Russian]. 7th edn., Vol. 1, Moscow pp 797

  18. Spurr RT (1982) The friction of polymers. Wear 79:301–310

    Article  Google Scholar 

  19. Muhlethaler K (1967) Ultrastructure and formation of plant cell walls. Annu Rev Plant Phys 42–18:1–24

  20. Newman RH (1999) Estimation of the lateral dimensions of cellulose crystallites using 13C NMR signal strengths. Sol St Nucl Magn Reson 15–29

  21. Revol F, Bradford H, Giasson J, Marchessault RH, Gray DG (1992) Helicoidal self-ordering of cellulose microfibrils in aqueous suspension. Int J Biol Macromol 14:170–172

    Article  Google Scholar 

  22. Ruben GC, Bokelman GH, Krakow W (1989) Triple-stranded left-hand helical cellulose microfibril in acetobacter xylinum and in tobacco primary cell wall. plant cell wall. Polym Biogenesis Biodegrad 399:78–298.1250

Download references

Author information

Authors and Affiliations

  1. N.N. Semenov Federal Research Center for Chemical Physics of Russian Academy of Science, Moscow, Russian Federation

    Aleksey Skoblin, Maria Mikhaleva & Sergey Stovbun

Authors
  1. Aleksey Skoblin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Maria Mikhaleva
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sergey Stovbun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aleksey Skoblin.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Skoblin, A., Mikhaleva, M. & Stovbun, S. Calculation of the strength of spirally organized cellulose fibers using the generalized Euler-Eitelwein formula. Meccanica 57, 1631–1637 (2022). https://doi.org/10.1007/s11012-022-01520-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-022-01520-w

Keywords

Search

Navigation