Skip to main content
SpringerLink
Log in

The correct derivation of the buckling equations of the shear-deformable FGM plates for the extended Kantorovich method

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

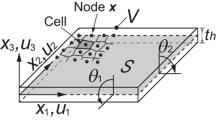
This article presents the derivation of the elastic buckling equations and boundary conditions of shear-deformable plates in the frame of the extended Kantorovich method (EKM). Surveying the literature shows that those stability equations are often obtained using a wrong derivation by confusing them with the linear equilibrium condition. This work aims at providing the correct derivation that is built on the stability of the equilibrium condition. Buckling equations are derived for three different plate theories, namely, the first-order shear deformation plate theory (FSDT), the refined-FSDT, and the refined plate theory (RPT). This article is the first to implement the EKM based on a refined theory. Also, it is the first time to implement the refined-FSDT in buckling analysis. For the generic FGM plates, buckling equations derived based on the FSDT and refined-FSDT are both found to be simple and contain only the lateral displacements/rotations variations. On the other hand, those of the RPT, have coupled lateral and in-plane displacement variations, even if the physical neutral plate is taken as the reference plane. The considered plate is rectangular and under general in-plane loads. The properties of the plate are continuously varying through its thickness which is assumed to change smoothly with a separable function in the two in-plane directions. The von Kármán nonlinearity is considered. The stability equations are derived according to the Trefftz criterion, using the variational calculus. The solution methods of the obtained equations are out of the scope of this article, however, a brief on the solution strategy is presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Chen PC (1972) Buckling analysis of a rectangular plate by the kantorovich method. Int J Mech Sci 14(1):15–24. https://doi.org/10.1016/0020-7403(72)90003-3

    Article  MATH  Google Scholar 

  2. Do VT, Pham VV, Nguyen HN (2020) On the development of refined plate theory for static bending behavior of functionally graded plates. Math Probl Eng. https://doi.org/10.1155/2020/2836763

    Article  MathSciNet  Google Scholar 

  3. Efraim E, Eisenberger M (2007) Exact vibration analysis of variable thickness thick annular isotropic and fgm plates. J Sound Vib 299(4):720–738. https://doi.org/10.1016/j.jsv.2006.06.068

    Article  Google Scholar 

  4. Eisenberger M, Alexandrov A (2003) Buckling loads of variable thickness thin isotropic plates. Thin-Walled Struct 41(9):871–889. https://doi.org/10.1016/S0263-8231(03)00027-2

    Article  Google Scholar 

  5. Eisenberger M, Shufrin I (2009) Buckling of plates by the multi-term extended Kantorovich method. In: 7th EUROMECH solid mechanics conference

  6. Eslami MR (2018) Buckling and postbuckling of beams, plates, and shells. Springer, Berlin

    Book  Google Scholar 

  7. Farahmand H (2020) Analytical solutions of bending and free vibration of moderately thick micro-plate via two-variable strain gradient theory. J Braz Soc Mech Sci Eng 42:1–11. https://doi.org/10.1007/s40430-020-02341-2

    Article  Google Scholar 

  8. Grimm TR, Gerdeen JC (1975) Instability analysis of thin rectangular plates using the kantorovich method. J Appl Mech 42(1):110–114. https://doi.org/10.1115/1.3423499

    Article  MATH  Google Scholar 

  9. Hassan AHA, Kurgan N (2020) Buckling of thin skew isotropic plate resting on pasternak elastic foundation using extended kantorovich method. Heliyon 6(6):e04236. https://doi.org/10.1016/j.heliyon.2020.e04236

    Article  Google Scholar 

  10. Hassan AHA, Kurgan N (2020) The relations between the various critical temperatures of thin fgm plates. J Appl Comput Mech 6:1404–1419. https://doi.org/10.22055/jacm.2020.34697.2459

    Article  Google Scholar 

  11. Jones RM (2006) Buckling of bars, plates, and shells. Bull Ridge Corporation

  12. Kantorovich L, Krylov V (1958) Approximate Methods of Higher Analysis. Interscience, New York

    MATH  Google Scholar 

  13. Kerr AD (1968) An extension of the kantorovich method. Q Appl Math 26(2):219–229

    Article  MathSciNet  Google Scholar 

  14. Kerr AD (1969) An extended kantorovich method for the solution of eigenvalue problems. Int J Solids Struct 5(6):559–572. https://doi.org/10.1016/0020-7683(69)90028-6

    Article  MATH  Google Scholar 

  15. Kerr AD, Alexander H (1968) An application of the extended kantorovich method to the stress analysis of a clamped rectangular plate. Acta Mech 6(2–3):180–196. https://doi.org/10.1007/BF01170382

    Article  MATH  Google Scholar 

  16. Lopatin A, Morozov E (2011) Buckling of the sscf rectangular orthotropic plate subjected to linearly varying in-plane loading. Compos Struct 93(7):1900–1909. https://doi.org/10.1016/j.compstruct.2011.01.024

    Article  Google Scholar 

  17. Lopatin A, Morozov E (2013) Buckling of a uniformly compressed rectangular sscf composite sandwich plate. Compos Struct 105:108–115. https://doi.org/10.1016/j.compstruct.2013.04.036

    Article  Google Scholar 

  18. Lopatin A, Morozov E (2014) Approximate buckling analysis of the ccff orthotropic plates subjected to in-plane bending. Int J Mech Sci 85:38–44. https://doi.org/10.1016/j.ijmecsci.2014.05.003

    Article  Google Scholar 

  19. Nguyen HN, Hong TT, Vinh PV, Quang ND, Thom DV et al (2019) A refined simple first-order shear deformation theory for static bending and free vibration analysis of advanced composite plates. Materials 12(15):2385. https://doi.org/10.3390/ma12152385

    Article  Google Scholar 

  20. Nguyen TK, Sab K, Bonnet G (2007) Shear correction factors for functionally graded plates. Mech Adv Mater Struct 14(8):567–575. https://doi.org/10.1080/15376490701672575

    Article  Google Scholar 

  21. Nguyen TK, Sab K, Bonnet G (2008) First-order shear deformation plate models for functionally graded materials. Compos Struct 83(1):25–36. https://doi.org/10.1016/j.compstruct.2007.03.004

    Article  Google Scholar 

  22. Qi Y, Knight NF Jr (1996) A refined first-order shear-deformation theory and its justification by plane strain bending problem of laminated plates. Int J Solids Struct 33(1):49–64. https://doi.org/10.1016/0020-7683(95)00010-8

    Article  MATH  Google Scholar 

  23. Reddy JN (2006) Theory and analysis of elastic plates and shells. CRC Press, Boca Raton

    Book  Google Scholar 

  24. Shariyat M, Alipour M (2014) A novel shear correction factor for stress and modal analyses of annular FGM plates with non-uniform inclined tractions and non-uniform elastic foundations. Int J Mech Sci 87:60–71. https://doi.org/10.1016/j.ijmecsci.2014.05.032

    Article  Google Scholar 

  25. Shimpi RP (2002) Refined plate theory and its variants. AIAA J 40(1):137–146. https://doi.org/10.2514/2.1622

    Article  Google Scholar 

  26. Shufrin I, Eisenberger M (2005) Stability and vibration of shear deformable plates - first order and higher order analyses. Int J Solids Struct 42(3):1225–1251. https://doi.org/10.1016/j.ijsolstr.2004.06.067

    Article  MATH  Google Scholar 

  27. Shufrin I, Eisenberger M (2005) Stability of variable thickness shear deformable plates - first order and high order analyses. Thin-Walled Struct 43(2):189–207. https://doi.org/10.1016/j.tws.2004.07.013

    Article  MATH  Google Scholar 

  28. Shufrin I, Eisenberger M (2006) Buckling of plates with variable in-plane forces. In: Analysis and Design of Plated Structures, 2: 26–55. Woodhead Publishing https://doi.org/10.1533/9781845690960.26

  29. Shufrin I, Eisenberger M (2007) Shear buckling of thin plates with constant in-plane stresses. Int J Struct Stab Dyn 7(02):179–192. https://doi.org/10.1142/S021945540700223X

    Article  MATH  Google Scholar 

  30. Shufrin I, Rabinovitch O, Eisenberger M (2008) Buckling of laminated plates with general boundary conditions under combined compression, tension, and shear-a semi-analytical solution. Thin-Walled Struct 46(7):925–938

    Article  Google Scholar 

  31. Shufrin I, Rabinovitch O, Eisenberger M (2008) Buckling of symmetrically laminated rectangular plates with general boundary conditions - a semi analytical approach. Compos Struct 82(4):521–531. https://doi.org/10.1016/j.compstruct.2007.02.003

    Article  MATH  Google Scholar 

  32. Shufrin I, Rabinovitch O, Eisenberger M (2008) Buckling of symmetrically laminated rectangular plates with general boundary conditions-a semi analytical approach. Compos Struct 82(4):521–531. https://doi.org/10.1016/j.compstruct.2007.02.003

    Article  MATH  Google Scholar 

  33. Singhatanadgid P, Singhanart T (2019) The kantorovich method applied to bending, buckling, vibration, and 3d stress analyses of plates: A literature review. Mech Adv Mater Struct 26(2):170–188. https://doi.org/10.1080/15376494.2017.1365984

    Article  Google Scholar 

  34. Tran HQ, Tran MT, Nguyen-Tri P et al (2020) A new four-variable refined plate theory for static analysis of smart laminated functionally graded carbon nanotube reinforced composite plates. Mech Mater 142:103294. https://doi.org/10.1016/j.mechmat.2019.103294

    Article  Google Scholar 

  35. Xie WC, Elishakoff I (2000) Buckling mode localization in rib-stiffened plates with misplaced stiffeners - kantorovich approach. Chaos Solitons Fractals 11(10):1559–1574. https://doi.org/10.1016/S0960-0779(99)00078-8

    Article  MATH  Google Scholar 

  36. Yu T, Zhang L (1986) The elastic wrinkling of an annular plate under uniform tension on its inner edge. Int J Mech Sci 28(11):729–737. https://doi.org/10.1016/0020-7403(86)90020-2

    Article  MATH  Google Scholar 

  37. Yuan S, Jin Y (1998) Computation of elastic buckling loads of rectangular thin plates using the extended kantorovich method. Comput Struct 66(6):861–867. https://doi.org/10.1016/S0045-7949(97)00111-9

    Article  MathSciNet  MATH  Google Scholar 

  38. Yuan S, Zhang Y (1992) Further extension of the extended kantorovich method. Comput Methods Eng Adv Appl 2:1240–1245

    Google Scholar 

  39. Zhang DG (2013) Modeling and analysis of fgm rectangular plates based on physical neutral surface and high order shear deformation theory. Int J Mech Sci 68:92–104. https://doi.org/10.1016/j.ijmecsci.2013.01.002

    Article  Google Scholar 

  40. Zhang DG, Zhou YH (2008) A theoretical analysis of fgm thin plates based on physical neutral surface. Comput Mater Sci 44(2):716–720. https://doi.org/10.1016/j.commatsci.2008.05.016

    Article  Google Scholar 

  41. Zhang L, Yu T (1988) The plastic wrinkling of an annular plate under uniform tension on its inner edge. Int J Solids Struct 24(5):497–503. https://doi.org/10.1016/0020-7683(88)90004-2

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, Engineering Faculty, Ondokuz Mayis University, 55139, Atakum, Samsun, Turkey

    Ahmed Hassan Ahmed Hassan, Naci Kurgan & Nihat Can

Authors
  1. Ahmed Hassan Ahmed Hassan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Naci Kurgan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nihat Can
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmed Hassan Ahmed Hassan.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hassan, A.H.A., Kurgan, N. & Can, N. The correct derivation of the buckling equations of the shear-deformable FGM plates for the extended Kantorovich method. Meccanica 57, 441–456 (2022). https://doi.org/10.1007/s11012-021-01441-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-021-01441-0

Keywords

Search

Navigation