Skip to main content
SpringerLink
Log in

Dynamic behavior investigation of capillary rising at various dominant forces using free energy lattice Boltzmann method

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

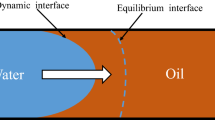
A Free Energy Lattice Boltzmann Method has been developed to characterize dominant forces and regimes involved in the capillary rise imbibition process. The comparison of the capillary rise behavior at the initial stages, reveals significant differences between numerical and theoretical models. This is attributed to the simplifying assumptions, ignoring the entrance region, dynamic contact angle, and inertial term in the theoretical model. By relaxing these assumptions in numerical formulations, the proposed model prevails the theoretical model limitations and shows closer results to the experimental records. However, as the capillary tube size decreases, the capillary force overcomes the inertia and the theoretical and numerical curves converge. Comparing the numerical curves and the experimental results indicates that the dynamics of the capillary ascent predicted by the present model is similar to the dry tube data. It should be mentioned that the inertial regime, the viscous regime, and the gravity-viscous regime can be considered as the successive regimes involved. Further investigations reveal a transition regime at the beginning of the process, which appears due to singular pressure loss. Therefore, the capillary rise phenomenon develops during these regimes as h ~ t2, h ~ t, h ~ t1/2 and relaxing to a constant value, respectively. Finally, for better understanding of the phenomenon, sensitivity analysis on the dominant forces has been performed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. De Gennes P-G, Brochard-Wyart F, Quéré D (2013) Capillarity and wetting phenomena: drops, bubbles, pearls, waves. Springer

  2. Lucas R (1918) The time law of the capillary rise of liquids. Kolloid Z 23:15–22

    Article  Google Scholar 

  3. Washburn EW (1921) The dynamics of capillary flow. Phys Rev 17(3):273

    Article  Google Scholar 

  4. Bosanquet C (1923) LV. On the flow of liquids into capillary tubes. Lond Edinb Dublin Philosop Mag J Sci 45(267):525–531

    Article  Google Scholar 

  5. Zhmud BV, Tiberg F, Hallstensson K (2000) Dynamics of Capillary Rise. J Colloid Interface Sci 228(2):263–269

    Article  Google Scholar 

  6. Szekely J, Neumann A, Chuang Y (1971) The rate of capillary penetration and the applicability of the Washburn equation. J Colloid Interface Sci 35(2):273–278

    Article  Google Scholar 

  7. Joos P, Van Remoortere P, Bracke M (1990) The kinetics of wetting in a capillary. J Colloid Interface Sci 136(1):189–197

    Article  Google Scholar 

  8. Hamraoui A, Nylander T (2002) Analytical approach for the Lucas-Washburn equation. J Colloid Interface Sci 250(2):415–421

    Article  Google Scholar 

  9. Hilpert M (2009) Effects of dynamic contact angle on liquid infiltration into horizontal capillary tubes:(Semi)-analytical solutions. J Colloid Interface Sci 337(1):131–137

    Article  Google Scholar 

  10. Heshmati M, Piri M (2014) Experimental investigation of dynamic contact angle and capillary rise in tubes with circular and noncircular cross sections. Langmuir 30(47):14151–14162

    Article  Google Scholar 

  11. Wu P, Nikolov A, Wasan D (2017) Capillary dynamics driven by molecular self-layering. Adv Coll Interface Sci 243:114–120

    Article  Google Scholar 

  12. Wu P, Nikolov AD, Wasan DT (2017) Capillary rise: validity of the dynamic contact angle models. Langmuir 33(32):7862–7872

    Article  Google Scholar 

  13. André J, Okumura K (2020) Capillary Replacement in a Tube Prefilled with a Viscous Fluid. Langmuir 36(37):10952–10959

    Article  Google Scholar 

  14. Lorenceau É et al (2002) Gravitational oscillations of a liquid column in a pipe. Phys Fluids 14(6):1985–1992

    Article  MATH  Google Scholar 

  15. Ichikawa N, Satoda Y (1994) Interface dynamics of capillary flow in a tube under negligible gravity condition. J Colloid Interface Sci 162(2):350–355

    Article  Google Scholar 

  16. Dreyer M, Delgado A, Path H-J (1994) Capillary rise of liquid between parallel plates under microgravity. J Colloid Interface Sci 163(1):158–168

    Article  Google Scholar 

  17. Weislogel MM, Lichter S (1998) Capillary flow in an interior corner. J Fluid Mech 373:349–378

    Article  MathSciNet  MATH  Google Scholar 

  18. Stange M, Dreyer ME, Rath HJ (2003) Capillary driven flow in circular cylindrical tubes. Phys Fluids 15(9):2587–2601

    Article  MATH  Google Scholar 

  19. Lu G, Wang X-D, Duan Y-Y (2013) Study on initial stage of capillary rise dynamics. Colloids Surf A 433:95–103

    Article  Google Scholar 

  20. Gunstensen AK et al (1991) Lattice Boltzmann model of immiscible fluids. Phys Rev A 43(8):4320

    Article  Google Scholar 

  21. Shan X, Chen H (1993) Lattice Boltzmann model for simulating flows with multiple phases and components. Phys Rev E 47(3):1815

    Article  Google Scholar 

  22. Shan X, Chen H (1994) Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys Rev E 49(4):2941

    Article  Google Scholar 

  23. Swift MR, Osborn W, Yeomans J (1995) Lattice Boltzmann simulation of nonideal fluids. Phys Rev Lett 75(5):830

    Article  Google Scholar 

  24. He X, Chen S, Zhang R (1999) A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability. J Comput Phys 152(2):642–663

    Article  MathSciNet  MATH  Google Scholar 

  25. Krüger T et al (2017) The lattice Boltzmann method. Springer 10(978–3):4–15

    Google Scholar 

  26. Mohamad A (2011) Lattice Boltzmann method, vol 70. Springer.

  27. Liu X, Guo Z (2013) A lattice Boltzmann study of gas flows in a long micro-channel. Comput Math Appl 65(2):186–193

    Article  MathSciNet  MATH  Google Scholar 

  28. Raiskinmäki P et al (2002) Lattice-Boltzmann simulation of capillary rise dynamics. J Stat Phys 107(1–2):143–158

    Article  MATH  Google Scholar 

  29. Attar E, Körner C (2009) Lattice Boltzmann method for dynamic wetting problems. J Colloid Interface Sci 335(1):84–93

    Article  Google Scholar 

  30. Wolf FG, Dos Santos LO, Philippi PC (2010) Capillary rise between parallel plates under dynamic conditions. J Colloid Interface Sci 344(1):171–179

    Article  Google Scholar 

  31. Wang D et al (2019) Direct Numerical Simulation of Capillary Rise in Microtubes with Different Cross-Sections. Acta Physica Polonica 135(3):1

    Google Scholar 

  32. Inamuro T et al (2004) A lattice Boltzmann method for incompressible two-phase flows with large density differences. J Comput Phys 198(2):628–644

    Article  MATH  Google Scholar 

  33. Lee T, Lin C-L (2005) A stable discretization of the lattice Boltzmann equation for simulation of incompressible two-phase flows at high density ratio. J Comput Phys 206(1):16–47

    Article  MathSciNet  MATH  Google Scholar 

  34. Zheng H, Shu C, Chew Y-T (2006) A lattice Boltzmann model for multiphase flows with large density ratio. J Comput Phys 218(1):353–371

    Article  MathSciNet  MATH  Google Scholar 

  35. Fries N, Dreyer M (2008) An analytic solution of capillary rise restrained by gravity. J Colloid Interface Sci 320(1):259–263

    Article  Google Scholar 

  36. Barry D et al (1993) A class of exact solutions for Richards’ equation. J Hydrol 142(1–4):29–46

    Article  Google Scholar 

  37. Jacqmin D (1999) Calculation of two-phase Navier-Stokes flows using phase-field modeling. J Comput Phys 155(1):96–127

    Article  MathSciNet  MATH  Google Scholar 

  38. Takada N et al (2001) Simulation of bubble motion under gravity by lattice Boltzmann method. J Nucl Sci Technol 38(5):330–341

    Article  Google Scholar 

  39. Cahn JW, Hilliard JE (1958) Free energy of a nonuniform system. I. Interfacial free energy. J Chem Phys 28(2):258–267

    Article  MATH  Google Scholar 

  40. Rowlinson JS, Widom (2013) Molecular theory of capillarity. Courier Corporation.

  41. Briant A, Yeomans J (2004) Lattice Boltzmann simulations of contact line motion: II: Binary fluids. Phys Rev E 69(3):1603

    Google Scholar 

  42. Briant AJ, Papatzacos P, Yeomans JM (2002) Lattice Boltzmann simulations of contact line motion in a liquid-gas system. Philos Trans A Math Phys Eng Sci 360(1792):485–495

    Article  MATH  Google Scholar 

  43. Delannoy J et al (2019) The dual role of viscosity in capillary rise. Soft Matter 15(13):2757–2761

    Article  Google Scholar 

  44. Fries N, Dreyer M (2008) The transition from inertial to viscous flow in capillary rise. J Colloid Interface Sci 327(1):125–128

    Article  Google Scholar 

Download references

Acknowledgements

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Funding

This research did not receive any specific grant from funding agencies.

Author information

Authors and Affiliations

  1. Institute of Petroleum Engineering, School of Chemical Engineering, College of Engineering, University of Tehran, Tehran, Iran

    Bijan Moradi, Shahab Ghasemi, Mohammad Reza Rasaei & Mozhdeh Sajjadi

  2. Department of Energy, Institute of Science and High Technology and Environmental Sciences, Graduate University of Advanced Technology, Kerman, Iran

    Amir Hosseini Moghadam

Authors
  1. Bijan Moradi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shahab Ghasemi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Amir Hosseini Moghadam
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mohammad Reza Rasaei
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mozhdeh Sajjadi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohammad Reza Rasaei.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Code availability

Custom code, C +  + .

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Moradi, B., Ghasemi, S., Hosseini Moghadam, A. et al. Dynamic behavior investigation of capillary rising at various dominant forces using free energy lattice Boltzmann method. Meccanica 56, 2961–2977 (2021). https://doi.org/10.1007/s11012-021-01426-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-021-01426-z

Keywords

Search

Navigation