Abstract
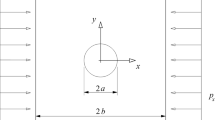
Porous metal bearings are widely used in small and micro devices. To compute the pressure one has to solve the Reynolds equation coupled with the Laplace equation. We show that it is possible to give to the relevant boundary value problem a variational formulation. We show that the pressure of the film in a porous bearing is less than that of the corresponding non-porous bearing.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
Taken here equal to zero in a suitable scale.
The conditions (12) are valid in the non-porous case. They are justified by the Lewy–Stampacchia theorem (see [6], and [7, p. 223]). For, the solution of the variational inequality which gives the unilateral solution is globally of class \(C^{1,\alpha }\). Hence, on the side of the free boundary where \(p=0\), we have \(p_{\theta }=0\), \(p_y=0\). This implies, by continuity, (12). The conditions valid on the free boundary in the porous case, are an open questions, see Sect. 6.
These constant can easily reintroduced with minor notational changes
To verify this relation, recall that \(\int _0^\pi \sin (mx)\sin (nx)dx\) is equal to \(\frac{\pi }{2}\) if \(m=n\) and equal to 0 if \(m\ne n\).
References
Brezis H (2010) Functional analysis, Sobolev spaces and partial differential equations. Springer, New York
Cameron A (1966) The principles of lubrication. Longmans, London
Cimatti G (1980) On the mathematical theory of porous metal bearings. Meccanica 2:112–117
Cimatti G (1977) On a problem of the theory of lubrication governed by a variational inequality. Appl Math Optim 3:227–242
Cohen SA (1987) A free boundary problem in lubrication theory. J Math Anal Appl 126:116–129
Kinderlehrer D, Stampacchia G (1980) An introduction to variational inequalities and their applications. Academic Press, London
Lewy H, Stampacchia G (1969) On the regularity of a variational inequality. Commun Pure Appl Math 22:153–188
Pinkus O, Sternlicht B (1961) Theory of hydrodynamic lubrication. McGraw-Hill Book Company, New York
Reynolds O (1886) On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments. Philos Trans R Soc Lond 177:157–234
Salsa S (2008) Partial differential equation in action-from modeling to theory. Springer, New York
Weiberger HF (1995) A first course in partial equations. Dover, New York
Acknowledgements
Several pertinent and useful remarks made by the Referee have been used to improve this paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Cimatti, G. A variational principle for the system of P.D.E. of porous metal bearings. Meccanica 56, 1079–1086 (2021). https://doi.org/10.1007/s11012-021-01322-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-021-01322-6