Thermal buckling and postbuckling behavior of FG-GRC laminated cylindrical shells with temperature-dependent material properties

Abstract

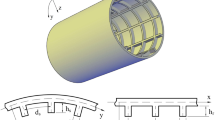
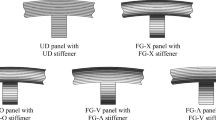
Thermal postbuckling analysis is presented for graphene-reinforced composite (GRC) laminated cylindrical shells under a uniform temperature field. The GRC layers are arranged in a functionally graded (FG) graphene reinforcement pattern by varying the graphene volume fraction in each GRC layer. The GRCs possess temperature dependent and anisotropic material properties and the extended Halpin–Tsai model is employed to evaluate the GRC material properties. The governing equations are based on a higher order shear deformation shell theory and include the von Kármán-type kinematic nonlinearity and the thermal effects. A singular perturbation method in conjunction with a two-step perturbation approach is applied to determine the thermal postbuckling equilibrium path for a GRC shell with or without geometric imperfection. An iterative scheme is developed to obtain numerical thermal buckling temperatures and thermal postbuckling load–deflection curves for the shells. The results reveal that the FG-X piece-wise FG graphene distribution can enhance the thermal postbuckling capacity of the shells when the shells are subjected to a uniform temperature loading.

Appendices

Appendix 1

In Eqs. (13b) and (14), the reduced stiffness matrices [A ^* _ij ], [B ^* _ij ], [D ^* _ij ], [E ^* _ij ], [F ^* _ij ] and [H ^* _ij ] are determined through relationships [46]

$$ {\mathbf{A}}^{*} = {\mathbf{A}}^{ - 1} ,\,\,{\mathbf{B}}^{*} = - {\mathbf{A}}^{ - 1} {\mathbf{B}},\,\,{\mathbf{E}}^{*} = - {\mathbf{A}}^{ - 1} {\mathbf{E}},\,\,{\mathbf{D}}^{*} = {\mathbf{D}} - {\mathbf{BA}}^{ - 1} {\mathbf{B}},\,\,{\mathbf{F}}^{*} = {\mathbf{F}} - {\mathbf{EA}}^{ - 1} {\mathbf{B}},\,\,{\mathbf{H}}^{*} = {\mathbf{H}} - {\mathbf{EA}}^{ - 1} {\mathbf{E}} $$

(32)

in which A_ij, B_ij, D_ij, etc., are the shell panel stiffnesses that are defined by

$$ (A_{ij} ,B_{ij} ,D_{ij} ,E_{ij} ,F_{ij} ,H_{ij} ) = \sum\limits_{k = 1}^{N} {\int\limits_{{t_{k - 1} }}^{{t_{k} }} {(\mathop {\bar{Q}_{ij} )_{k} }\limits^{{}} } } (1,Z,Z^{2} ,Z^{3} ,Z^{4} ,Z^{6} )dZ\quad \left( {i,j = 1,2,6} \right) $$

(33a)

$$ (A_{ij} ,D_{ij} ,F_{ij} ) = \sum\limits_{k = 1}^{N} {\int\limits_{{t_{k - 1} }}^{{t_{k} }} {(\mathop {\bar{Q}_{ij} )_{k} }\limits^{{}} } } (1,Z^{2} ,Z^{4} )dZ\quad \left( {i,j = 4,5} \right) $$

(33b)

Appendix 2

The solutions W, Ψ_x, Ψ_y and F in the thermal postbuckling region may be expressed as

$$ \begin{aligned} W & = \varepsilon \left[ {A_{00}^{(1)} - A_{00}^{(1)} \left( {a_{01}^{(1)} \cos \phi \frac{x}{\sqrt \varepsilon }} \right.} \right. + a_{10}^{(1)} \left. {\sin \phi \frac{x}{\sqrt \varepsilon }} \right)\exp \left( { - \vartheta \frac{x}{\sqrt \varepsilon }} \right) \\ & \quad - \left. { A_{00}^{(1)} \left( {a_{01}^{(1)} \cos \phi \frac{\pi - x}{\sqrt \varepsilon }} \right. + a_{10}^{(1)} \left. {\sin \phi \frac{\pi - x}{\sqrt \varepsilon }} \right)\exp \left( { - \vartheta \frac{\pi - x}{\sqrt \varepsilon }} \right)} \right] \\ & \quad + \varepsilon^{2} \left[ {A_{11}^{(2)} \sin mx\sin ny + A_{02}^{(2)} \cos 2ny} \right. \\ & \quad - A_{02}^{(2)} (\cos 2ny)\left( {a_{01}^{(1)} \cos \phi \frac{x}{\sqrt \varepsilon } + } \right.a_{10}^{(1)} \left. {\sin \phi \frac{x}{\sqrt \varepsilon }} \right)\exp \left( { - \vartheta \frac{x}{\sqrt \varepsilon }} \right) \\ & \quad - A_{02}^{(2)} (\cos 2ny)\left( {a_{01}^{(1)} \cos \phi \frac{\pi - x}{\sqrt \varepsilon } + } \right.a_{10}^{(1)} \left. {\sin \phi \frac{\pi - x}{\sqrt \varepsilon }} \right)\left. {\exp \left( { - \vartheta \frac{\pi - x}{\sqrt \varepsilon }} \right)} \right] \\ & \quad + \varepsilon^{3} \left[ {A_{11}^{(3)} \sin mx\sin ny + A_{02}^{(3)} \cos 2ny\left. {} \right]} \right. + \varepsilon^{4} \left[ {A_{00}^{(4)} + A_{11}^{(4)} \sin mx\sin ny} \right. \\ & \quad + A_{20}^{(4)} \cos 2mx + A_{02}^{(4)} \cos 2ny + A_{13}^{(4)} \sin mx\sin 3ny + A_{04}^{(4)} \cos 4ny\left. {} \right] + O(\varepsilon^{5} ) \\ \end{aligned} $$

(34)

$$ \begin{aligned} \Psi_{x} & = \varepsilon^{3/2} \left[ {A_{00}^{(1)} c_{10}^{(3/2)} \sin \phi \frac{x}{\sqrt \varepsilon }} \right.\exp \left( { - \vartheta \frac{x}{\sqrt \varepsilon }} \right) + A_{00}^{(1)} c_{10}^{(3/2)} \sin \phi \frac{\pi - x}{\sqrt \varepsilon }\left. {\exp \left( { - \vartheta \frac{\pi - x}{\sqrt \varepsilon }} \right)} \right] \\ & \quad + \varepsilon^{2} [C_{11}^{(2)} \cos mx\sin ny] + \varepsilon^{5/2} \left[ {A_{02}^{(2)} (\cos 2ny)c_{10}^{(5/2)} \sin \phi \frac{x}{\sqrt \varepsilon }} \right.\exp \left( { - \vartheta \frac{x}{\sqrt \varepsilon }} \right) \\ & \quad + A_{02}^{(2)} (\cos 2ny)c_{10}^{(5/2)} \sin \phi \frac{\pi - x}{\sqrt \varepsilon }\left. {\exp \left( { - \vartheta \frac{\pi - x}{\sqrt \varepsilon }} \right)} \right] + \varepsilon^{3} [C_{11}^{(3)} \cos mx\sin ny] \\ & \quad + \varepsilon^{4} [C_{11}^{(4)} \cos mx\sin ny + C_{20}^{(4)} \sin 2mx + C_{13}^{(4)} \cos mx\sin 3ny] + O(\varepsilon^{5} ) \\ \end{aligned} $$

(35)

$$ \begin{aligned} \Psi_{y} & = \varepsilon^{2} [D_{11}^{(2)} \sin mx\cos ny] + \varepsilon^{3} [D_{11}^{(3)} \sin mx\cos ny + D_{02}^{(3)} \sin 2ny \\ & \quad - (A_{02}^{(2)} 2n\beta \sin 2ny)\left( {d_{01}^{(3)} \cos \phi \frac{x}{\sqrt \varepsilon } + d_{10}^{(3)} \sin \phi \frac{x}{\sqrt \varepsilon }} \right)\exp \left( { - \vartheta \frac{x}{\sqrt \varepsilon }} \right) \\ & \quad - (A_{02}^{(2)} 2n\beta \sin 2ny)\left( {d_{01}^{(3)} \cos \phi \frac{\pi - x}{\sqrt \varepsilon } + d_{10}^{(3)} \sin \phi \frac{\pi - x}{\sqrt \varepsilon }} \right)\left. {\exp \left( { - \vartheta \frac{\pi - x}{\sqrt \varepsilon }} \right)} \right] \\ & \quad + \varepsilon^{4} [D_{11}^{(4)} \sin mx\cos ny + D_{02}^{(4)} \sin 2ny + D_{13}^{(4)} \sin mx\cos 3ny] + O(\varepsilon^{5} ) \\ \end{aligned} $$

(36)

$$ \begin{aligned} F & = - B_{00}^{(0)} \frac{{y^{2} }}{2} + \varepsilon \left[ { - B_{00}^{(1)} \frac{{y^{2} }}{2}} \right] + \varepsilon^{2} \left[ { - B_{00}^{(2)} \frac{{y^{2} }}{2} + B_{11}^{(2)} \sin mx\sin ny} \right. \\ & \quad + A_{00}^{(1)} \left( {b_{01}^{(2)} \cos \phi \frac{x}{\sqrt \varepsilon } + b_{10}^{(2)} \sin \phi \frac{x}{\sqrt \varepsilon }} \right)\exp \left( { - \vartheta \frac{x}{\sqrt \varepsilon }} \right) \\ & \quad + A_{00}^{(1)} \left( {b_{01}^{(2)} \cos \phi \frac{\pi - x}{\sqrt \varepsilon } + b_{10}^{(2)} \sin \phi \frac{\pi - x}{\sqrt \varepsilon }} \right)\left. {\exp \left( { - \vartheta \frac{\pi - x}{\sqrt \varepsilon }} \right)} \right] \\ & \quad + \varepsilon^{3} \left[ { - B_{00}^{(3)} \frac{{y^{2} }}{2} + B_{02}^{(3)} \cos 2ny} \right. \\ & \quad + A_{02}^{(2)} (\cos 2ny)\left( {b_{01}^{(3)} \cos \phi \frac{x}{\sqrt \varepsilon } + b_{10}^{(3)} \sin \phi \frac{x}{\sqrt \varepsilon }} \right)\exp \left( { - \vartheta \frac{x}{\sqrt \varepsilon }} \right) \\ & \quad + A_{02}^{(2)} (\cos 2ny)\left( {b_{01}^{(3)} \cos \phi \frac{\pi - x}{\sqrt \varepsilon } + b_{10}^{(3)} \sin \phi \frac{\pi - x}{\sqrt \varepsilon }} \right)\left. {\exp \left( { - \vartheta \frac{\pi - x}{\sqrt \varepsilon }} \right)} \right] \\ & \quad + \varepsilon^{4} \left[ { - B_{00}^{(4)} \frac{{y^{2} }}{2} + B_{20}^{(4)} \cos 2mx + B_{02}^{(4)} \cos 2ny + B_{13}^{(4)} \sin mx\sin 3ny} \right] + O(\varepsilon^{5} ) \\ \end{aligned} $$

(37)

In the above equations, all coefficients are related and can be expressed in terms of A ⁽²⁾₁₁ , whereas ϑ and φ are given in detail in “Appendix 3”.

Appendix 3

In Eqs. (29) and (30)

$$ \begin{aligned} \Theta_{3} & = \frac{1}{{C_{3} }}\left[ {\gamma_{14} \gamma_{24} \frac{{m^{4} (1 + \mu )}}{{16n^{2} \beta^{2} g_{09} g_{06} }}\varepsilon^{ - 1} - \gamma_{24} \gamma_{14} \frac{{m^{2} g_{11} }}{{32n^{2} \beta^{2} g_{09} }}} \right. \\ & \quad + \frac{1}{8}\frac{{\gamma_{5} }}{{g_{8} }}\left[ {m^{2} (1 + 2\mu )\varepsilon - 2g_{05} \varepsilon^{2} + \frac{{g_{05}^{2} }}{{m^{2} }}\varepsilon^{3} } \right] + \left. {\frac{{\gamma_{24}^{2} - \gamma_{5}^{2} }}{{\gamma_{24} }}\frac{{\gamma_{T2} }}{{g_{T} }}\lambda_{T}^{(2)} } \right], \\ \Theta_{4} & = \frac{{\gamma_{24}^{2} - \gamma_{5}^{2} }}{{\gamma_{24} }}\frac{{\gamma_{T2} }}{{g_{T} }}\lambda_{T}^{(0)} , \\ \end{aligned} $$

(38)

$$ \begin{aligned} \lambda_{x}^{(0)} & = \frac{1}{2}\left\{ {\frac{{\gamma_{24} m^{2} }}{{(1 + \mu )g_{06} }}\varepsilon^{ - 1} + \gamma_{24} \frac{{g_{05} + (1 + \mu )g_{07} }}{{(1 + \mu )^{2} g_{06} }}} \right. \\ & \quad + \frac{1}{{\gamma_{14} (1 + \mu )m^{2} }}\left[ {g_{08} + \gamma_{14} \gamma_{24} \frac{{g_{05} }}{{g_{06} }}\frac{{(1 + \mu )g_{07} - \mu (2 + \mu )g_{05} }}{{(1 + \mu )^{2} }}} \right]\varepsilon \\ & \quad \left. { - \frac{\mu }{{(1 + \mu )^{2} }}\frac{{g_{05} }}{{\gamma_{14} m^{4} }}\left[ {1 + \frac{{g_{05} }}{{(1 + \mu )m^{2} }}\varepsilon } \right]\,\left[ {g_{08} + \gamma_{14} \gamma_{24} \frac{{g_{05} }}{{g_{06} }}\frac{{g_{05} + (1 + \mu )g_{07} }}{{(1 + \mu )^{2} }}(2 + \mu )} \right]\varepsilon^{2} } \right\}, \\ \lambda_{x}^{(2)} & = \frac{1}{8}\left\{ {\gamma_{14} \gamma_{24}^{2} \frac{{m^{6} \left( {2 + \mu } \right)}}{{2g_{09} g_{06}^{2} }}\varepsilon^{ - 1} } \right. \\ & \quad + \gamma_{14} \gamma_{24}^{2} \frac{{m^{4} }}{{2g_{09}^{{}} g_{06} }}\left[ {\frac{{g_{05} }}{{g_{06} }} + \frac{{g_{07} }}{{g_{06} }}(1 + \mu ) + g_{12} (1 + \mu ) - \frac{1}{(1 + \mu )}g_{11} } \right] \\ & \quad - \frac{1}{4}\gamma_{24} m^{2} g_{13} (1 + 2\mu )\varepsilon + \gamma_{14} \gamma_{24}^{2} \frac{{m^{2} g_{11} }}{{2g_{09} }}\left[ {\frac{{g_{05} }}{{g_{06} }}\frac{1}{1 + \mu } - \frac{{g_{07} }}{{g_{06} }} - g_{12} } \right]\varepsilon \\ & \quad + \gamma_{14} \gamma_{24}^{2} \frac{{m^{2} g_{05} }}{{2g_{09} g_{06} }}\left[ {\frac{{2(1 + \mu )^{2} - (1 + 2\mu )}}{{2(1 + \mu )^{2} }}g_{14} + \frac{\mu }{1 + \mu }\frac{{g_{05} }}{{g_{06} }}} \right](2 + \mu )\varepsilon \\ & \quad \left. { + \gamma_{24} \frac{{m^{2} n^{4} \beta^{4} }}{{g_{06} }}\frac{{(5 + 11\mu + 4\mu^{2} )g_{06} + 8m^{4} (1 + \mu )(2 + \mu )g_{10} }}{{(1 + \mu )g_{06} - 4m^{4} g_{10} }}\varepsilon } \right\}, \\ \lambda_{x}^{(4)} & = \frac{1}{128}\gamma_{14}^{2} \gamma_{24}^{3} \frac{{m^{10} (1 + \mu )}}{{g_{09}^{2} g_{06}^{3} }}\frac{{(6 + 6\mu + \mu^{2} )g_{136} + (1 + \mu )(6 - \mu^{2} )g_{06} }}{{g_{136} - (1 + \mu )g_{06} }}\varepsilon^{ - 1} , \\ \lambda_{T}^{(0)} & = 2\lambda_{x}^{(0)} , \\ \lambda_{T}^{(2)} & = 2\lambda_{x}^{(2)} - \frac{1}{8}\frac{{\gamma_{24} }}{{g_{8} }}\left\{ {m^{2} (1 + 2\mu )\varepsilon - 2g_{05} \varepsilon^{2} + \frac{{g_{05}^{2} }}{{m^{2} }}\varepsilon^{3} } \right\}, \\ \lambda_{T}^{(4)} & = 2\lambda_{x}^{(4)} + \frac{1}{64}\frac{{\gamma_{24} }}{{g_{8} }}\left\{ {\frac{{b_{11} }}{32\pi \vartheta }} \right.\gamma_{14}^{2} \gamma_{24}^{2} \frac{{m^{8} (1 + \mu )^{2} }}{{n^{4} \beta^{4} g_{09}^{2} g_{06}^{2} }}\varepsilon^{ - 3/2} \\ & \quad + m^{2} n^{4} \beta^{4} (1 + \mu )^{2} \varepsilon^{3} \left. {\left[ {\frac{{g_{06} (1 + 2\mu ) + 8m^{4} (1 + \mu )g_{10} }}{{g_{06} (1 + \mu ) - 4m^{4} g_{10} }}} \right]^{2} } \right\}, \\ \end{aligned} $$

(39)

in which g_ij and g_ijk are defined as in Shen [40] and

$$ \begin{aligned} & b = \left[ {\frac{{\gamma_{14} \gamma_{24} \gamma_{320}^{2} }}{{g_{16} }}} \right]^{1/2} ,\quad c = \gamma_{14} \gamma_{24} \gamma_{320} \frac{{g_{15} }}{{2g_{16} }},\quad \vartheta = \left[ {\frac{b - c}{2}} \right]^{1/2} \quad \phi = \left[ {\frac{b + c}{2}} \right]^{1/2} , \\ & a_{01}^{(1)} = 1,\quad a_{10}^{(1)} = \frac{\vartheta }{\phi },\quad b_{01}^{(2)} = \gamma_{24} g_{19} ,\quad b_{10}^{(2)} = \gamma_{24} \frac{\vartheta }{\phi }g_{20} , \\ & b_{11} = \frac{1}{b}[(a_{10}^{(1)} )^{2} \phi^{2} b + a_{10}^{(1)} 2\vartheta \phi c + (2\vartheta^{4} - \vartheta^{2} \phi^{2} + \phi^{4} )], \\ & C_{3} = 1 - \frac{{g_{05} }}{{m^{2} }}\varepsilon ,\quad C_{11} = \frac{{g_{8} }}{{g_{T} }},\quad g_{8} = \gamma_{24}^{2} - \frac{2}{\pi }\frac{{\gamma_{5}^{2} }}{{\gamma_{24} }}(\vartheta b_{01}^{(2)} - \phi b_{10}^{(2)} )\varepsilon^{1/2} , \\ & g_{T} = (\gamma_{24}^{2} \gamma_{T1} - \gamma_{5} \gamma_{T2} ) + \frac{2}{\pi }\frac{{\gamma_{5} }}{{\gamma_{24} }}(\vartheta b_{01}^{(2)} - \phi b_{10}^{(2)} )(\gamma_{T2} - \gamma_{5} \gamma_{T1} )\varepsilon^{1/2} , \\ \end{aligned} $$

(40)