Abstract
Soft materials and structures have recently attracted lots of research interests as they provide paramount potential applications in diverse fields including soft robotics, wearable devices, stretchable electronics and biomedical engineering. In a previous work, an Euler–Bernoulli finite strain beam model with thickness stretching effect was proposed for soft thin structures subject to stiff constraint in the width direction. By extending that model to account for the transverse shear effect, a Timoshenko-type finite strain beam model within the plane-strain context is developed in the present work. With some kinematic hypotheses, the finite deformation of the beam is analyzed, constitutive equations are deduced from the theory of finite elasticity, and by employing the standard variational method, the equilibrium equations and associated boundary conditions are derived. In the limit of infinitesimal strain, the new model degenerates to the classical extensible and shearable elastica model. The corresponding incremental equilibrium equations and associated boundary conditions are also obtained. Based on the new beam model, analytical solutions are given for simple deformation modes, including uniaxial tension, simple shear, pure bending, and buckling under an axial load. Furthermore, numerical solution procedures and results are presented for cantilevered beams and simply supported beams with immovable ends. The results are also compared with the previously developed finite strain Euler–Bernoulli beam model to demonstrate the significance of transverse shear effect for soft beams with a small length-to-thickness ratio. The developed beam model will contribute to the design and analysis of soft robots and soft devices.







Similar content being viewed by others
References
Antman SS (1974) Kirchhoff’s problem for nonlinearly elastic rods. Q Appl Math 32:221–240
Attard MM (2003) Finite strain—beam theory. IJSS 40:4563–4584
Attard MM, Hunt GW (2008) Column buckling with shear deformations—a hyperelastic formulation. Int J Solids Struct 45:4322–4339
Attard MM, Kim M-Y (2010) Lateral buckling of beams with shear deformations—a hyperelastic formulation. Int J Solids Struct 47:2825–2840
Auricchio F, Carotenuto P, Reali A (2008) On the geometrically exact beam model: a consistent, effective and simple derivation from three-dimensional finite-elasticity. Int J Solids Struct 45:4766–4781
Beatty MF (1987) Topics in finite elasticity: hyperelasticity of rubber, elastomers, and biological tissues—with examples. ApMRv 40:1699–1734
Betsch P, Steinmann P (2002) Frame-indifferent beam finite elements based upon the geometrically exact beam theory. Int J Numer Meth Eng 54:1775–1788
Carrera E (2002) Theories and finite elements for multilayered, anisotropic, composite plates and shells. Arch Comput Methods Eng 9:87–140
Carrera E, Giunta G, Petrolo M (2011) Beam structures: classical and advanced theories. Wiley, Hoboken
Chan BQY, Low ZWK, Heng SJW, Chan SY, Owh C, Loh XJ (2016) Recent advances in shape memory soft materials for biomedical applications. ACS Appl Mater Interfaces 8:10070–10087
Gaharwar AK, Peppas NA, Khademhosseini A (2014) Nanocomposite hydrogels for biomedical applications. Biotechnol Bioeng 111:441–453
Ge Q, Qi HJ, Dunn ML (2013) Active materials by four-dimension printing. Appl Phys Lett 103:131901
Gladman AS, Matsumoto EA, Nuzzo RG, Mahadevan L, Lewis JA (2016) Biomimetic 4D printing. Nat Mater 15:413–418
He L, Lou J, Dong Y, Kitipornchai S, Yang J (2018) Variational modeling of plane-strain hyperelastic thin beams with thickness stretching effect. Acta Mech. https://doi.org/10.1007/s00707-018-2258-4
He L, Lou J, Du J, Wang J (2017) Finite bending of a dielectric elastomer actuator and pre-stretch effects. IJMS 122:120–128
He L, Yan S, Li B, Zhao G, Chu J (2013) Adhesion model of side contact for an extensible elastic fiber. IJSS 50:2659–2666
Hong S, Sycks D, Chan HF, Lin S, Lopez GP, Guilak F, Leong KW, Zhao X (2015) 3D printing of highly stretchable and tough hydrogels into complex, cellularized structures. Adv Mater 27:4035–4040
Ibrahimbegović A (1995) On finite element implementation of geometrically nonlinear Reissner’s beam theory: three-dimensional curved beam elements. Comput Methods Appl Mech Eng 122:11–26
Irschik H, Gerstmayr J (2009) A continuum mechanics based derivation of Reissner’s large-displacement finite-strain beam theory: the case of plane deformations of originally straight Bernoulli-Euler beams. Acta Mech 206:1–21
Irschik H, Gerstmayr J (2011) A continuum-mechanics interpretation of Reissner’s non-linear shear-deformable beam theory. Math Comput Model Dyn Syst 17:19–29
Jeong J-W, Shin G, Park SI, Yu KJ, Xu L, Rogers JA (2015) Soft materials in neuroengineering for hard problems in neuroscience. Neuron 86:175–186
Kempaiah R, Nie Z (2014) From nature to synthetic systems: shape transformation in soft materials. J Mater Chem B 2:2357–2368
Khoo ZX, Teoh JEM, Liu Y, Chua CK, Yang S, An J, Leong KF, Yeong WY (2015) 3D printing of smart materials: a review on recent progresses in 4D printing. Virtual Phys Prototyp 10:103–122
Kim S, Laschi C, Trimmer B (2013) Soft robotics: a bioinspired evolution in robotics. Trends Biotechnol 31:287–294
Lu T, Huang J, Jordi C, Kovacs G, Huang R, Clarke DR, Suo Z (2012) Dielectric elastomer actuators under equal-biaxial forces, uniaxial forces, and uniaxial constraint of stiff fibers. Soft Matter 8:6167–6173
Lubbers LA, van Hecke M, Coulais C (2017) A nonlinear beam model to describe the postbuckling of wide neo-Hookean beams. J Mech Phys Solids 106:191–206
Magnusson A, Ristinmaa M, Ljung C (2001) Behaviour of the extensible elastica solution. IJSS 38:8441–8457
Majidi C (2014) Soft robotics: a perspective—current trends and prospects for the future. Soft Robot 1:5–11
Mata P, Oller S, Barbat A (2007) Static analysis of beam structures under nonlinear geometric and constitutive behavior. Comput Methods Appl Mech Eng 196:4458–4478
Nachbagauer K, Pechstein AS, Irschik H, Gerstmayr J (2011) A new locking-free formulation for planar, shear deformable, linear and quadratic beam finite elements based on the absolute nodal coordinate formulation. Multibody SysDyn 26:245–263
Ogden RW (1997) Non-linear elastic deformations. Courier Corporation, Chelmsford
Reddy JN (2006) Theory and analysis of elastic plates and shells. CRC Press, Boca Raton
Reissner E (1972) On one-dimensional finite-strain beam theory: the plane problem. Zeitschrift für angewandte Mathematik und Physik: ZAMP 23:795–804
Rogers JA, Someya T, Huang Y (2010) Materials and mechanics for stretchable electronics. Science 327:1603–1607
Rudykh S, Bhattacharya K (2012) Snap-through actuation of thick-wall electroactive balloons. Int J Non-Linear Mech 47:206–209
Rus D, Tolley MT (2015) Design, fabrication and control of soft robots. Nature 521:467–475
Simo JC (1985) A finite strain beam formulation. The three-dimensional dynamic problem. Part I. CMAME 49:55–70
Simo JC, Vu-Quoc L (1991) A geometrically-exact rod model incorporating shear and torsion-warping deformation. Int J Solids Struct 27:371–393
Son D, Lee J, Qiao S, Ghaffari R, Kim J, Lee JE, Song C, Kim SJ, Lee DJ, Jun SW (2014) Multifunctional wearable devices for diagnosis and therapy of movement disorders. Nat Nanotechnol 9:397–404
Song J (2015) Mechanics of stretchable electronics. Curr Opin Solid State Mater Sci 19:160–170
Suo Z (2012) Mechanics of stretchable electronics and soft machines. MRS Bull 37:218–225
Ventola CL (2014) Medical applications for 3D printing: current and projected uses. Pharm Ther 39:704
Yükseler RF (2015) A theory for rubber-like rods. Int J Solids Struct 69:350–359
Zeng W, Shu L, Li Q, Chen S, Wang F, Tao XM (2014) Fiber-based wearable electronics: a review of materials, fabrication, devices, and applications. Adv Mater 26:5310–5336
Zhao X, Suo Z (2007) Method to analyze electromechanical stability of dielectric elastomers. Appl Phys Lett 91:061921
Zupan E, Saje M, Zupan D (2013) On a virtual work consistent three-dimensional Reissner–Simo beam formulation using the quaternion algebra. AcMec 224:1709–1729
Acknowledgements
The work described in this paper was fully supported by the Australian Research Council Grant under Discovery Project scheme (DP160101978). The authors are very grateful for these financial supports. Dr. He and Dr. Lou are also grateful for the support from National Natural Science Foundation of China (Grant Nos. 11602118 and 11602117) and also sponsored by K.C. Wong Magna Fund in Ningbo University.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
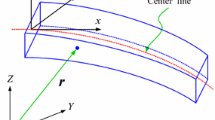
Following Simo’s method [37], the direct notation is adopted here to facilitate the derivation of the constitutive equations for the present plane-strain beam model. The position of any material point in the deformed configuration is denoted by \({\mathbf{x}} = {\mathbf{x}}\left( {X,Z} \right)\)\(= {\mathbf{x}}_{0} \left( X \right) + z^{*} \left( Z \right){\mathbf{e}}_{\varphi } \left( X \right)\), where \({\mathbf{x}}_{0}\) is the corresponding point on the geometrical mid plane, \({\mathbf{e}}_{\varphi }\) is the unit vector reflecting the rotation of the deformed cross-section, and the possible dependence of \(z^{*}\) on \(X\) is neglected as argued in the kinematic analysis in Sect. 2.1. Since \({\mathbf{e}}_{\varphi }\) is a unit vector, we have \({{\partial {\mathbf{e}}_{\varphi } } \mathord{\left/ {\vphantom {{\partial {\mathbf{e}}_{\varphi } } {\partial X}}} \right. \kern-0pt} {\partial X}} = {\varvec{\upomega}} \times {\mathbf{e}}_{\varphi } , \, {\dot{\mathbf{e}}}_{\varphi } = {\mathbf{w}} \times {\mathbf{e}}_{\varphi } ,\) where \({\varvec{\upomega}}\) is the rotation rate of \({\mathbf{e}}_{\varphi }\) along the arc-length, i.e., the nominal curvature, and \({\mathbf{w}}\) the spin rate (per unit time interval) at a fixed cross-section with the over-dot denoting the material time derivative.
The deformation gradient and the first Piola–Kirchhoff stress tensor are given respectively by:
where \({\mathbf{E}}_{I} \left( {I = 1,2} \right)\) is the unit basis vector in the reference configuration, \(X_{I}\)\(\left( {I = 1,2} \right)\) represent the reference coordinates \(\left( {X,Z} \right)\), \({\mathbf{T}}_{I} \left( {I = 1,2} \right)\) are the stress vectors (per unit reference area) in the current configuration. By the balance law of angular momentum, we have \({\mathbf{F}}^{T} {\mathbf{P}} = {\mathbf{P}}^{T} {\mathbf{F}}\), or equivalently, \({{\partial {\mathbf{x}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{x}}} {\partial X_{I} }}} \right. \kern-0pt} {\partial X_{I} }} \times {\mathbf{T}}_{I} = {\mathbf{0}}\).
With the assumed kinematics, the deformation gradient and its material time derivative can be written, respectively, as:
Hence, the stress power per unit reference volume can be obtained:
Using the balance law of angular momentum, we have:
Considering that \({\varvec{\upomega}} \times \left\{ {{\mathbf{w}} \times \left( {{\mathbf{x}} - {\mathbf{x}}_{0} } \right)} \right\} - {\mathbf{w}} \times \left\{ {{\varvec{\upomega}} \times \left( {{\mathbf{x}} - {\mathbf{x}}_{0} } \right)} \right\} = \left( {{\varvec{\upomega}} \times {\mathbf{w}}} \right) \times \left( {{\mathbf{x}} - {\mathbf{x}}_{0} } \right)\), we obtain:
Neglecting the last two small terms relevant to the thickness stretching in comparison with the dominant stretching, shearing and bending power, the integral can be rewritten as:
where \({\mathbf{N}} = \int_{A} {{\mathbf{T}}_{1} {\text{d}}A}\), \({\mathbf{M}} = \int_{A} {\left( {{\mathbf{x}} - {\mathbf{x}}_{0} } \right) \times {\mathbf{T}}_{1} {\text{d}}A}\) and \({\varvec{\Gamma}} = {{\partial {\mathbf{x}}_{0} } \mathord{\left/ {\vphantom {{\partial {\mathbf{x}}_{0} } {\partial X}}} \right. \kern-0pt} {\partial X}}\) physically means the internal force vector, internal moment vector and the axial stretch vector, respectively, and \(\mathop {\left( \cdot \right)}\limits^{\nabla }\) represents the corotational rate (an objective rate) defined by \(\mathop {\left( \cdot \right)}\limits^{\nabla } = {{\partial \left( \cdot \right)} \mathord{\left/ {\vphantom {{\partial \left( \cdot \right)} {\partial t}}} \right. \kern-0pt} {\partial t}} - {\mathbf{w}} \times \left( \cdot \right).\)
Decomposing the internal force vector into normal and shear components \(N_{n}\) and \(N_{s}\) on the deformed cross-section, and equivalently, replacing the material-time derivative or objective rates with variations in the above formula, we have:
where \(\lambda_{n} = \lambda \cos \alpha - 1\), \(\gamma = \lambda \sin \alpha\), and \(\delta \phi = \int_{A} {{\mathbf{P}} \cdot \delta {\mathbf{F}}{\text{d}}A} = \delta \int_{A} {W{\text{d}}A}\). Finally, we derive the constitutive relation (13) by localization.
Appendix 2
The tangent tensile stiffness, shear stiffness, bending stiffness and coupling stiffnesses are defined and also calculated, based on the constitutive Eq. (21)1–3 for neo-Hookean beams, as follows:
where \(K_{T}\), \(K_{S}\) and \(K_{M}\) are the stretching stiffness, the shear stiffness and the bending stiffness, and \(K_{TS}\), \(K_{TM}\) and \(K_{SM}\) are the stretching-shear coupling stiffness, the stretching-bending coupling stiffness and the shear-bending coupling stiffness. These formulae clearly show the effect of the mid-plane stretch on the magnitude of each stiffness.
Rights and permissions
About this article
Cite this article
He, L., Lou, J., Dong, Y. et al. A shearable and thickness stretchable finite strain beam model for soft structures. Meccanica 53, 3759–3777 (2018). https://doi.org/10.1007/s11012-018-0905-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-018-0905-4