Skip to main content
SpringerLink
Log in

Effect of irregularity and heterogeneity on the stresses produced due to a normal moving load on a rough monoclinic half-space

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

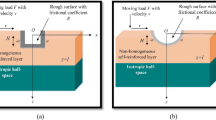
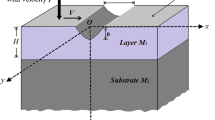
The present study aims to study the normal and shear stresses produced in a rough irregular heterogeneous monoclinic half-space due to a normal moving load. Closed form expressions of normal and shear stresses have been obtained. It is observed that both normal stress and shear stress are affected not only by depth, the frictional coefficient on a rough surface, and the maximum depth of irregularity but also by the heterogeneity and types of irregularity in the medium. The comparative study has been made to analyze the effect of different types of irregularity on both the stresses. There is a significant effect of depth, frictional coefficient, heterogeneity, maximum depth of irregularity and irregularity factor on the normal and shear stresses in both heterogeneous monoclinic and heterogeneous isotropic medium. A comparison is made to study the effects of the said parameters on the normal and shear stress produced in both heterogeneous medium. These effects are highlighted and depicted by means of graphs. As a special case of the problem, the stress produced due to normal moving load in an isotropic half-space with and without heterogeneity, irregularity has been discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31

Similar content being viewed by others

References

  1. Achenbach JD, Keshava SP, Herrmann G (1967) Moving load on a plate resting on an elastic half space. J Appl Math Mech 34:910–914

    Google Scholar 

  2. Alekseyeva LA (2007) The dynamics of an elastic half-space under the action of a moving load. J Appl Math Mech 71:511–518

    Article  MathSciNet  Google Scholar 

  3. Chattopadhay A, Gupta S, Sharma VK, Pato Kumari (2011) Stresses produced on a rough irregular half-space by a moving load. Acta Mech 221:271–280

    Article  Google Scholar 

  4. Chattopadhyay A, Singh AK (2012) Propagation of magnetoelastic shear waves in an irregular self-reinforced layer. J Eng Math 75:139–155

    Article  MathSciNet  MATH  Google Scholar 

  5. Chattopadhyay A, Gupta S, Sahu SA, Singh AK (2011) Dispersion equation of magnetoelastic shear waves in an irregular monoclinic layer. Appl Math Mech 32:571–586

    Article  MathSciNet  MATH  Google Scholar 

  6. Chattopadhyay A, Saha S (2006) Dynamic response of normal moving load in the plane of symmetry of a monoclinic half space. Tamkang J Sci Eng 9:307

    Google Scholar 

  7. Chattopadhyay A, Sahu SA, Singh AK (2013) Dispersion of SH waves in an irregular non homogeneous self-reinforced crustal layer over a semi-infinite self-reinforced medium. J Vib Control 19:109–119

    Article  MathSciNet  Google Scholar 

  8. Chattopadhyay A, Singh AK (2012) G-type seismic waves in fibre reinforced media. Meccanica 47:1775–1785

    Article  MathSciNet  MATH  Google Scholar 

  9. Chonan S (1976) Moving load on a pre-stressed plate resting on a fluid half-space. Arch Appl Mech 45:171–178

    MATH  Google Scholar 

  10. Cole J, Huth J (1958) Stresses produced in a half plane by moving loads. J Appl Mech 25:433–436

    MathSciNet  MATH  Google Scholar 

  11. Craggs JW (1960) On two-dimensional wave in an elastic half plane. Proc Camb Philos Soc 56:269–275

    Article  MathSciNet  MATH  ADS  Google Scholar 

  12. Gubbins D (1990) Seismology and plate tectonics. Cambridge University Press, Cambridge 170

    Google Scholar 

  13. Kraus EH, Hunt WF, Ramsdell LS (1936) Mineralogy: an introduction to the study of minerals and crystals. McGraw-Hill, New York

    Google Scholar 

  14. Lee HP, Ng TY (1994) Dynamic response of a cracked beam subject to a moving load. Acta Mech 106:221–230

    Article  MATH  Google Scholar 

  15. Mason WP (1964) Piezo-electric crystals and their application to ultrasonic. D Van Nostrand Company, New York

    Google Scholar 

  16. Miles IW (1966) Response of a layered half space to a moving load. J Appl Mech 33:680–681

    Article  Google Scholar 

  17. Mukherjee S (1969) Stresses produced by a load moving over a rough boundary of a semi-infinite transversely isotopic solid. Pure Appl Geophys 72:45–50

    Article  ADS  Google Scholar 

  18. Mukhopadhyay A (1965) Stress produced by a normal moving load over a transversely isotropic layer of ice lying on a rigid foundation. Pure Appl Geophys 60:29

    Article  ADS  Google Scholar 

  19. Olsson M (1991) On the fundamental moving load problem. J Sound Vib 145:299–307

    Article  ADS  Google Scholar 

  20. Othman MIA, Said SM (2014) 2D problem of magneto-thermoelasticity fiber-reinforced medium under temperature dependent properties with three-phase-lag model. Meccanica 49:1225–1241

    Article  MathSciNet  MATH  Google Scholar 

  21. Sackman JL (1961) Uniformly moving load on a layered half plane. J Eng Mech Div Proc ASCE. 87:75–89

    Google Scholar 

  22. Selim MM (2007) Static deformation of an irregular initially stressed medium. Appl Math Comput 188:1274–1284

    Article  MathSciNet  MATH  Google Scholar 

  23. Sharma V, Kumar S (2014) Velocity dispersion in an elastic plate with microstructure: effects of characteristic length in a couple stress model. Meccanica 49:1083–1090

    Article  MathSciNet  MATH  Google Scholar 

  24. Sneddon IN (1952) Stress produced by a pulse of pressure moving along the surface of semi-infinite solid. Rend Del Circ Matem di Paler 2:57–62

    Article  MathSciNet  Google Scholar 

  25. Tiersten HF (1969) Linear Piezo-electric plate vibration. Plenum Press, New York

    Book  Google Scholar 

  26. Ungar A (1976) Wave generation in an elastic half-space by a normal point load moving uniformly over the free surface. Int J Eng Sci 14:935–945

    Article  MATH  Google Scholar 

Download references

Acknowledgments

The authors convey their sincere thanks to Indian School of Mines, Dhanbad for providing JRF to Mr. Santan Kumar and also facilitating us with its best facility for research.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Indian School of Mines, Dhanbad, 826004, Jharkhand, India

    Abhishek Kumar Singh, Santan Kumar & Amares Chattopadhyay

Authors
  1. Abhishek Kumar Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Santan Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Amares Chattopadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abhishek Kumar Singh.

Appendices

Appendix I

$$ \begin{aligned} a = C_{44}^{0} - C_{22}^{0} q^{2} - \rho^{0} V^{2} ,\quad b = \left( {C_{42}^{0} + C_{24}^{0} } \right)q, \hfill \\ c = \left( {C_{24}^{0} q^{2} - C_{43}^{0} } \right),\quad d = \left( {C_{23}^{0} + C_{44}^{0} } \right)q, \hfill \\ \end{aligned} $$
$$ \begin{aligned} a_{1} = C_{42}^{0} q^{2} - C_{34}^{0} ,\quad b_{1} = \left( {C_{44}^{0} + C_{32}^{0} } \right)q, \hfill \\ c_{1} = \left( { - \rho^{0} V^{2} + C_{33}^{0} - C_{44}^{0} q^{2} } \right),\quad d_{1} = \left( {C_{43}^{0} + C_{34}^{0} } \right)q, \hfill \\ \end{aligned} $$
$$ \begin{aligned} A^{'} = \left( {C_{44}^{0} - \rho V^{2} } \right),\quad B^{'} = \left( {C_{23}^{0} + C_{44}^{0} } \right),\quad C^{'} = \left( {C_{42}^{0} + C_{24}^{0} } \right),\, \hfill \\ D^{'} = \left( {A^{'} B^{'} - C^{'} C_{43}^{0} } \right),\quad E^{'} = \left( {C^{'} C_{24}^{0} - C_{22}^{0} B^{'} } \right),\quad F^{'} = \left( {C_{34}^{0} + C_{43}^{0} } \right), \hfill \\ G^{'} = \left( {C_{44}^{0} + C_{32}^{0} } \right),\quad H^{'} = \left( {C_{33}^{0} - \rho V^{2} } \right),\quad I^{'} = \left( {C_{42}^{0} F^{'} - G^{'} C_{44}^{0} } \right), \hfill \\ J^{'} = \left( {G^{'} H^{'} - C_{34}^{0} F^{'} } \right),\quad K^{'} = \left( {F^{'2} - 2C_{44}^{0} H^{'} } \right),\quad Y = \left( {B^{'2} - 2C_{24}^{0} C_{43}^{0} } \right), \hfill \\ \end{aligned} $$
$$ \begin{aligned} a_{0} & = E^{'} C_{44}^{02} + I^{'} C_{24}^{02} ,\quad 3b_{0} = \left[ {D^{'} C_{44}^{02} + E^{'} K^{'} + I^{'} Y + J^{'} C_{24}^{02} } \right], \\ 3c_{0} & = \left[ {D^{'} K^{'} + E^{'} H^{'2} + I^{'} C_{43}^{02} + J^{'} Y} \right],\quad d_{0} = D^{'} H^{'2} + J^{'} C_{43}^{02} , \\ \end{aligned} $$
$$ Z = a_{0} x + b_{0} ,\quad H = a_{0} c_{0} - b_{0}^{2} ,\quad G = a_{0}^{2} d_{0} - 3a_{0} b_{0} c_{0} + 2b_{0}^{3} , $$
$$ s_{1} = \left\{ {\frac{1}{2}\left[ { - G + \sqrt {G^{2} + 4H^{3} } } \right]} \right\}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} ,\quad n_{1} = \left\{ {\frac{1}{2}\left[ { - G - \sqrt {G^{2} + 4H^{3} } } \right]} \right\}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} ,\quad x = q^{2} , $$
$$ \begin{aligned} t_{1} = C_{22}^{0} q_{1} + m_{1} C_{23}^{0} ,\quad t_{2} = C_{22}^{0} q_{2} + m_{2} C_{23}^{0} ,\quad t_{3} = \left( {q_{1} m_{1} - 1} \right)C_{24}^{0} ,\quad t_{4} = \left( {q_{2} m_{2} - 1} \right)C_{24}^{0} , \hfill \\ t_{5} = C_{42}^{0} q_{1} + m_{1} C_{43}^{0} ,\quad t_{6} = C_{42}^{0} q_{2} + m_{2} C_{43}^{0} ,\quad t_{7} = \left( {m_{1} q_{1} - 1} \right)C_{44}^{0} ,\quad t_{8} = \left( {m_{2} q_{2} - 1} \right)C_{44}^{0} , \hfill \\ \end{aligned} $$
$$ D_{1} = \left| {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & {t_{3} } & {t_{4} } \\ { - t_{3} } & { - t_{4} } & {t_{1} } & {t_{2} } \\ {t_{5} } & {t_{6} } & {t_{7} } & {t_{8} } \\ { - t_{7} } & { - t_{8} } & {t_{5} } & {t_{6} } \\ \end{array} } \right|. $$

Appendix II

$$ A = \left| {\begin{array}{*{20}c} {\frac{1}{\pi }} & {t_{2} } & {t_{3} } & {t_{4} } \\ 0 & { - t_{4} } & {t_{1} } & {t_{2} } \\ {\frac{1}{\pi }} & {t_{6} } & {t_{7} } & {t_{8} } \\ 0 & { - t_{8} } & {t_{5} } & {t_{6} } \\ \end{array} } \right|,\,\,B = \left| {\begin{array}{*{20}c} {t_{1} } & {\frac{1}{\pi }} & {t_{3} } & {t_{4} } \\ { - t_{3} } & 0 & {t_{1} } & {t_{2} } \\ {t_{5} } & {\frac{R}{\pi }} & {t_{7} } & {t_{8} } \\ { - t_{7} } & 0 & {t_{5} } & {t_{6} } \\ \end{array} } \right|,\,\,C = \left| {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & {\frac{1}{\pi }} & {t_{4} } \\ { - t_{3} } & { - t_{4} } & 0 & {t_{2} } \\ {t_{5} } & {t_{6} } & {\frac{R}{\pi }} & {t_{8} } \\ { - t_{7} } & { - t_{8} } & 0 & {t_{6} } \\ \end{array} } \right|,\,\,D = \left| {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & {t_{3} } & {\frac{1}{\pi }} \\ { - t_{3} } & { - t_{4} } & {t_{1} } & 0 \\ {t_{5} } & {t_{6} } & {t_{7} } & {\frac{R}{\pi }} \\ { - t_{7} } & { - t_{8} } & {t_{5} } & 0 \\ \end{array} } \right| $$
$$ E_{1} = \left| {\begin{array}{*{20}c} { - S_{1} } & {t_{2} } & {t_{3} } & {t_{4} } \\ { - S_{3} } & { - t_{4} } & {t_{1} } & {t_{2} } \\ { - S_{5} } & {t_{6} } & {t_{7} } & {t_{8} } \\ { - S_{7} } & { - t_{8} } & {t_{5} } & {t_{6} } \\ \end{array} } \right|,\,\,E_{2} = \left| {\begin{array}{*{20}c} { - S_{2} } & {t_{2} } & {t_{3} } & {t_{4} } \\ { - S_{4} } & { - t_{4} } & {t_{1} } & {t_{2} } \\ { - S_{6} } & {t_{6} } & {t_{7} } & {t_{8} } \\ { - S_{8} } & { - t_{8} } & {t_{5} } & {t_{6} } \\ \end{array} } \right|,\,\,F_{1} = \left| {\begin{array}{*{20}c} {t_{1} } & { - S_{1} } & {t_{3} } & {t_{4} } \\ { - t_{3} } & { - S_{3} } & {t_{1} } & {t_{2} } \\ {t_{5} } & { - S_{5} } & {t_{7} } & {t_{8} } \\ { - t_{7} } & { - S_{7} } & {t_{5} } & {t_{6} } \\ \end{array} } \right|,\,\, $$
$$ F_{2} = \left| {\begin{array}{*{20}c} {t_{1} } & { - S_{2} } & {t_{3} } & {t_{4} } \\ { - t_{3} } & { - S_{4} } & {t_{1} } & {t_{2} } \\ {t_{5} } & { - S_{6} } & {t_{7} } & {t_{8} } \\ { - t_{7} } & { - S_{8} } & {t_{5} } & {t_{6} } \\ \end{array} } \right|,\,\,G_{1} = \left| {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & { - S_{1} } & {t_{4} } \\ { - t_{3} } & { - t_{4} } & { - S_{3} } & {t_{2} } \\ {t_{5} } & {t_{6} } & { - S_{5} } & {t_{8} } \\ { - t_{7} } & { - t_{8} } & { - S_{7} } & {t_{6} } \\ \end{array} } \right|,\,\,G_{2} = \left| {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & { - S_{2} } & {t_{4} } \\ { - t_{3} } & { - t_{4} } & { - S_{4} } & {t_{2} } \\ {t_{5} } & {t_{6} } & { - S_{6} } & {t_{8} } \\ { - t_{7} } & { - t_{8} } & { - S_{8} } & {t_{6} } \\ \end{array} } \right|,\,\, $$
$$ H_{1} = \left| {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & {t_{3} } & { - S_{1} } \\ { - t_{3} } & { - t_{4} } & {t_{1} } & { - S_{3} } \\ {t_{5} } & {t_{6} } & {t_{7} } & { - S_{5} } \\ { - t_{7} } & { - t_{8} } & {t_{5} } & { - S_{7} } \\ \end{array} } \right|,\,\,H_{2} = \left| {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & {t_{3} } & { - S_{2} } \\ { - t_{3} } & { - t_{4} } & {t_{1} } & { - S_{4} } \\ {t_{5} } & {t_{6} } & {t_{7} } & { - S_{6} } \\ { - t_{7} } & { - t_{8} } & {t_{5} } & { - S_{8} } \\ \end{array} } \right|,\,\, $$
$$ \begin{aligned} \alpha_{1} = \frac{\det A}{{\det D_{1} }},\quad \alpha_{2} = \frac{\det B}{{\det D_{1} }},\quad \alpha_{3} = \frac{\det C}{{\det D_{1} }},\quad \alpha_{4} = \frac{\det D}{{\det D_{1} }},\quad \alpha_{5} = \frac{{\det E_{1} }}{{\det D_{1} }},\quad \alpha_{6} = \frac{{\det E_{2} }}{{\det D_{1} }}, \hfill \\ \alpha_{7} = \frac{{\det F_{1} }}{{\det D_{1} }},\quad \alpha_{8} = \frac{{\det F_{2} }}{{\det D_{1} }},\quad \alpha_{9} = \frac{{\det G_{1} }}{{\det D_{1} }},\quad \alpha_{10} = \frac{{\det G_{2} }}{{\det D_{1} }},\quad \alpha_{11} = \frac{{\det H_{1} }}{{\det D_{1} }},\quad\alpha_{12} = \frac{{\det H_{2} }}{{\det D_{1} }}, \hfill \\ \end{aligned} $$
$$S_{1} = \alpha_{1} t_{1} + \alpha_{2} t_{2} + \alpha_{3} t_{3} + \alpha_{4} t_{4} ,\quad S_{2} = - \left( {\alpha_{1} t_{1} q_{1} + \alpha_{2} t_{2} q_{2} + \alpha_{3} t_{3} q_{1} + \alpha_{4} t_{4} q_{2} } \right),\quad S_{3} = - \alpha_{1} t_{3} - \alpha_{2} t_{4} + \alpha_{3} t_{1} + \alpha_{4} t_{2} ,\quad S_{4} = \alpha_{1} t_{3} q_{1} + \alpha_{2} t_{4} q_{2} - \alpha_{3} t_{1} q_{1} - \alpha_{4} t_{2} q_{2} ,\quad S_{5} = \alpha_{1} t_{5} + \alpha_{2} t_{6} + \alpha_{3} t_{7} + \alpha_{4} t_{8} ,\quad S_{6}= - \left( {\alpha_{1} t_{5} q_{1} + \alpha_{2} t_{6} q_{2} + \alpha_{3} t_{1} q_{1} + \alpha_{4} t_{8} q_{2} } \right),\quad S_{7} = - \alpha_{1} t_{7} - \alpha_{2} t_{8} + \alpha_{3} t_{5} + \alpha_{4} t_{6} ,\quad S_{8} = \alpha_{1} t_{7} q_{1} + \alpha_{2} t_{8} q_{2} - \alpha_{3} t_{5} q_{1} - \alpha_{4} t_{6} q_{2} , $$
$$ \begin{aligned} Q_{1} = \alpha_{1} + \varepsilon h\upsilon \alpha_{5} ,\quad Q_{2} = \varepsilon h\alpha_{6} ,\quad Q_{3} = \alpha_{3} + \varepsilon h\upsilon \alpha_{9} ,\quad Q_{4} = \varepsilon h\alpha_{10} ,\, \hfill \\ Q_{5} = \alpha_{2} + \varepsilon h\upsilon \alpha_{7} ,\quad Q_{6} = \varepsilon h\alpha_{8} ,\quad Q_{7} = \alpha_{4} + \varepsilon h\upsilon \alpha_{11} ,\quad Q_{8} = \varepsilon h\alpha_{12} , \hfill \\ \end{aligned} $$
$$ \begin{aligned} \phi_{1} = q_{1}^{2} y^{2} + \left( {z - Vt} \right)^{2} ,\quad \phi_{2} = q_{2}^{2} y^{2} + \left( {z - Vt} \right)^{2} , \hfill \\ \phi_{3} = q_{1}^{2} y^{2} - \left( {z - Vt} \right)^{2} ,\quad \phi_{4} = q_{2}^{2} y^{2} - \left( {z - Vt} \right)^{2} . \hfill \\ \end{aligned} $$

Appendix III

$$ \begin{aligned} t_{1}^{'} &= \left( {\lambda + 2\mu } \right)q_{1}^{'} + m_{1}^{'} \lambda , \hfill \\ \,t_{2}^{'} &= \left( {\lambda + 2\mu } \right)q_{2}^{'} + m_{2}^{'} \lambda , \hfill \\ \,t_{3}^{'} &= t_{4}^{'} = t_{5}^{'} = t_{6}^{'} = 0, \hfill \\ \,t_{7}^{'} & = \left( {m_{1}^{'} q_{1}^{'} - 1} \right)\mu , \hfill \\ \,t_{8}^{'} & = \left( {q_{2}^{'} m_{2}^{'} - 1} \right)\mu . \hfill \\ \end{aligned} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Singh, A.K., Kumar, S. & Chattopadhyay, A. Effect of irregularity and heterogeneity on the stresses produced due to a normal moving load on a rough monoclinic half-space. Meccanica 49, 2861–2878 (2014). https://doi.org/10.1007/s11012-014-0033-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-014-0033-8

Keywords

Search

Navigation