Skip to main content
SpringerLink
Log in

Dual solutions of a mixed convection flow near the stagnation point region over an exponentially stretching/shrinking sheet in nanofluids

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

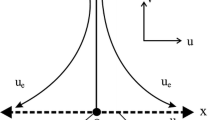
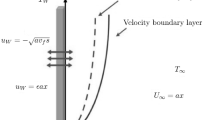
The aim of this paper is to study the development of mixed convection flow near the stagnation point region over an exponentially stretching/shrinking sheet in nanofluids. The external flow, stretching velocity and wall temperature are assumed to vary as prescribed exponential functions. Using the local similarity method, it has been shown that dual solutions of velocity and temperature exist for certain values of suction/injection, mixed convection, nanoparticle volume fraction and stretching/shrinking parameters. The transformed non-linear ordinary differential equations along with the boundary conditions form a two point boundary value problem and are solved using Shooting method, by converting into an initial value problem. In this method, the system of equations is converted into a set of first order system which is solved by fourth-order Runge–Kutta method. Three different types of nanoparticles, namely copper (Cu), aluminum oxide (Al2O3) and titanium oxide (TiO2) are considered by using water-based fluid with Prandtl number Pr = 6.2. It is also found that the skin friction coefficient and the heat transfer rate at the surface are highest for Copper–water nanofluids as compared to Al2O3. The effect of the solid volume fraction parameter φ of the nanofluids on the heat transfer characteristics is also investigated. The results indicate that dual solutions exist only for shrinking sheet. The effects of various parameters on the velocity and temperature profiles are also presented here.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Abbreviations

a,b :

Constants

ɛ :

Skin friction coefficient

C p :

Specific heat at constant pressure

f :

Dimensionless streamfunction

F :

Dimensionless velocity

g :

Acceleration due to gravity

Gr :

Grash of number

k :

Thermal conductivity

L :

Reference length

Nu :

Nusselt number

Pr:

Prandtl number, Pr = ν f /α f

q w :

Surface heat flux

Re:

Reynolds number, Re = u e L/v f

T:

Fluid temperature in the boundary layer

u, v :

Velocity components in the x- and y- directions, respectively

u e :

Velocity of the external flow

u w :

Velocity of the stretching surface

x, y :

Cartesian coordinates measured along the surface and normal to it, respectively

α :

Thermal diffusivity

β :

Volumetric coefficient of thermal expansion

ɛ :

Stretching/shrinking parameter, ɛ = b/a

η :

Similarity variable

θ :

Dimensionless temperature

λ :

Mixed convection parameter

μ :

Dynamic viscosity

ν :

Kinematic viscosity

ρ :

Fluid density

τ w :

Surface heat flux

φ :

Nanoparticle volume fraction

ψ :

Dimensional streamfunction

e :

Condition at the edge of the boundary layer

w :

Condition at the wall

∞:

Freestream condition

nf :

Nanofluid

f :

Fluid

s :

Solid

References

  1. Ding Y, Chen H, Wang L, Yang CY, He Y, Yang W, Lee WP, Zhang L, Huo R (2007) Heat transfer intensification using nanofluids. Kona 25:23–38

    Article  Google Scholar 

  2. Das SK, Choi SUS, Yu W, Pradeep T (2007) Nanofluids: science and technology. Wiley, Hoboken

    Book  Google Scholar 

  3. Magyari E, Keller B (1999) Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J Phys D Appl Phys 32:577–585

    Article  ADS  Google Scholar 

  4. Bidin B, Nazar R (2009) Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur J Sci Res 33:710–717

    Google Scholar 

  5. Ishak A (2011) MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malays 40:391–395

    Google Scholar 

  6. Arifin NM, Nazar R, Pop I (2011) Non-isobaric Marangoni boundary layer flow for Cu, Al2O3 and TiO2 nanoparticles in a water based fluid. Meccanica 46:833–843

    Article  MATH  MathSciNet  Google Scholar 

  7. Chamkha AJ, Abbasbandy S, Rashad AM, Vajravelu K (2013) Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid. Meccanica 48:275–285

    Article  MathSciNet  Google Scholar 

  8. Ahmed Sameh E, Abd El-Aziz MM (2013) Effect of local thermal non-equilibrium on unsteady heat transfer by natural convection of a nanofluid over a vertical wavy surface. Meccanica 48:33–43

    Article  MathSciNet  Google Scholar 

  9. Anbuchezhian N, Srinivasan K, Chandrasekaran K, Kandasamy R (2013) Magneto hydrodynamic effects on natural convection flow of a nanofluid in the presence of heat source due to solar energy. Meccanica 48:307–321

    Article  MathSciNet  Google Scholar 

  10. Al-Odat MQ, Damseh RA, Al-Azab TA (2006) Thermal boundary layer on an exponentially stretching continuous surface in the presence of magnetic field effect. Int J Appl Mech Eng 11:289–299

    MATH  Google Scholar 

  11. Sajid M, Hayat T (2008) Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int Commun Heat Mass Transf 35:347–356

    Article  Google Scholar 

  12. Bhattacharyya K, Vajravelu K (2012) Stagnation-point flow and heat transfer over an exponentially shrinking sheet. Commun Nonlinear Sci Numer Simulat 17:2728–2734

    Article  ADS  Google Scholar 

  13. Bachok Norfifah, Ishak Anuar, Pop Ioan (2012) Boundary layer stagnation-point flow and heat transfer over an exponentially stretching/shrinking sheet in a nanofluid. Int J Heat Mass Transf 55:8122–8128

    Article  Google Scholar 

  14. Kumari M, Nath G (2014) Steady mixed convection flow of Maxwell fluid over an exponentially stretching vertical surface with magnetic field and viscous dissipation. Meccanica 49:1263–1274

    Article  MATH  MathSciNet  Google Scholar 

  15. Kameswaran PK, Narayana M, Sibanda P, Murthy PVSN (2012) Hydromagnetic nanofluid flow due to a stretching or shrinking sheet with viscous dissipation and chemical reaction effects. Int J Heat Mass Transf 55:7587–7595

    Article  Google Scholar 

  16. Lok YY, Pop I (2014) Stretching or shrinking sheet problem for unsteady separated stagnation point flow. Meccanica 49:1479–1492

    Article  MATH  MathSciNet  Google Scholar 

  17. Mukhopadhyay S (2013) Effects of thermal radiation and variable fluid viscosity on stagnation point flow past a porous stretching sheet. Meccanica 48:1717–1730

    Article  MathSciNet  Google Scholar 

  18. Mahapatra TR, Nandy SK (2013) Slip effects on unsteady stagnation point flow and heat transfer over a shrinking sheet. Meccanica 48:1599–1606

    Article  MathSciNet  Google Scholar 

  19. Mahapatra TR, Nandy SK, Gupta AS (2012) Oblique stagnation point flow and heat transfer towards a shrinking sheet with thermal radiation. Meccanica 47:1325–1335

    Article  MathSciNet  Google Scholar 

  20. Nadeem S, Hussain A, Khan M (2010) HAM solutions for boundary layer flow in the region of the stagnation point towards a stretching sheet. Commun Nonlinear Sci Numer Simulat 15:475–481

    Article  MATH  MathSciNet  ADS  Google Scholar 

  21. Layek GC, Mukhopadhyay S, Samad SKA (2007) Heat and mass transfer analysis for boundary layer stagnation point flow towards a heated porous stretching sheet with heat absorption/generation and suction/blowing. Int Commun Heat Mass Transf 34:347–356

    Article  Google Scholar 

  22. Ishak A, Nazar R, Pop I (2006) Mixed convection boundary layers in the stagnation point flow towards a stretching vertical sheet. Meccanica 41:509–518

    Article  MATH  Google Scholar 

  23. Ishak A, Nazar R, Pop I (2009) Boundary layer flow and heat transfer over an unsteady stretching vertical surface. Meccanica 44:369–375

    Article  MATH  MathSciNet  Google Scholar 

  24. Anilkumar Devarapu (2011) Nonsimilar solutions for unsteady mixed convection from a moving vertical plate. Comm Nonlinear Sci Numer Simul 16:3147–3157

    Article  MATH  MathSciNet  Google Scholar 

  25. Pal Dulal (2010) Mixed convection heat transfer in the boundary layers on an exponentially stretching surface with magnetic field. Appl Math Comput 217:2356–2369

    Article  MATH  MathSciNet  Google Scholar 

  26. Abu-Nada E, Masoud Z, Oztop HF, Compo A (2010) Effect of nanofluid variable properties on natural convection in enclosures. Int J Therm Sci 49:479–491

    Article  Google Scholar 

  27. Oztop HF, Abu-Nada E (2008) Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int J Heat Fluid Flow 29:1326–1336

    Article  Google Scholar 

  28. Aziz A (2009) A similarity solution for laminar thermal boundary layer over a flat plate with convective surface boundary condition. Comm Nonlinear Sci Numer Simul 14:1064–1068

    Article  MathSciNet  Google Scholar 

  29. Ishak A (2010) Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Appl Math Comput 217:837–842

    Article  MATH  MathSciNet  Google Scholar 

  30. Makinde OD, Aziz A (2010) MHD mixed convection from a vertical plate embedded in a porous medium with a convective boundary condition. Int J Therm Sci 49:1813–1820

    Article  Google Scholar 

  31. Makinde OD (2010) On MHD heat and mass transfer over a moving vertical plate with a convective surface boundary condition. Can J Chem Eng 88:983–990

    Google Scholar 

  32. Ridha A (1996) Aiding flows non-unique similarity solutions of mixed-convection boundary- layer equations. J Appl Math Phys 47:341–352

    Article  MATH  MathSciNet  Google Scholar 

  33. Subhashini SV, Samuel Nancy, Pop I (2011) Effects of buoyancy assisting and opposing flows on mixed convection boundary layer flow over a permeable vertical surface. Int Commun Heat Mass Transf 38:499–503

    Article  Google Scholar 

  34. Subhashini SV, Samuel Nancy, Pop I (2011) Double-diffusive convection from a permeable vertical surface under convective boundary condition. Int Commun Heat Mass Transf 38:1183–1188

    Article  Google Scholar 

  35. Subhashini SV, Sumathi R, Pop I (2012) Dual solutions in a double- diffusive convection near stagnation point region over a stretching vertical surface. Int J Heat Mass Transf 55:2524–2530

    Article  Google Scholar 

  36. Zwillinger D (1992) Handbook of differential equations, 2nd edn. Academic press, New York

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Anna University, Chennai, 600 025, India

    S. V. Subhashini & R. Sumathi

  2. School of Computational and Applied Mathematics, University of the Witwatersrand, Private Bag – 3, Wits, Johannesburg, 2050, South Africa

    E. Momoniat

Authors
  1. S. V. Subhashini
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Sumathi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. E. Momoniat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. V. Subhashini.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Subhashini, S.V., Sumathi, R. & Momoniat, E. Dual solutions of a mixed convection flow near the stagnation point region over an exponentially stretching/shrinking sheet in nanofluids. Meccanica 49, 2467–2478 (2014). https://doi.org/10.1007/s11012-014-0016-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-014-0016-9

Keywords

Search

Navigation