Skip to main content
SpringerLink
Log in

Effect of rotation on a fiber-reinforced thermo-elastic under Green-Naghdi theory and influence of gravity

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

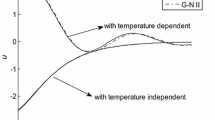
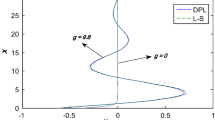
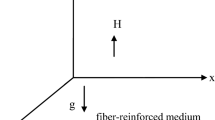
A general model of the equation of Green-Naghdi theory (G-N), which is applied to study the influence of reinforcement on the total deformation for an infinite space weakened by a finite linear opening thermal shock, is solved. We study the influence of reinforcement on the total deformation of a rotating thermo-elastic half-space and the mutual interaction under the influence of gravity. The material is homogeneous, isotropic and elastic half-space. The methodology applied here consists of the use of a normal mode analysis to obtain the exact expressions for the temperature, the displacement components, and the stress components. Some particular cases are also discussed in this context. The deformation of a body depends on the nature of the force applied as well as the type of boundary conditions. The variations of the variables considered with the horizontal distance are illustrated graphically. Comparisons are made with the results predicted by the type II and type III cases in the presence and in the absence of the effect of fiber reinforcement. It is found that reinforcement, rotation, and gravity have great effect on the distribution of the field quantities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Belfield AJ, Rogers TG, Spencer AJM (1983) Stress in elastic plates reinforced by fiber lying in concentric circles. J Mech Phys Solids 31:25–54

    Article  ADS  MATH  Google Scholar 

  2. Verma PDS, Rana OH (1983) Rotation of a circular cylindrical tube reinforced by fibres lying along helices. Mech Mater 2:353–359

    Article  Google Scholar 

  3. Verma PDS (1986) Magnetoelastic shear waves in self-reinforced bodies. Int J Eng Sci 24:1067–1073

    Article  MATH  Google Scholar 

  4. Singh B (2006) Wave propagation in thermally conducting linear fibre-reinforced composite materials. Arch Appl Mech 75:513–520

    Article  MATH  Google Scholar 

  5. Sengupta PR, Nath S (2001) Surface waves in fibre-reinforced anisotropic elastic media. Sãdhanã 26:363–370

    Google Scholar 

  6. Hashin Z, Rosen WB (1964) The elastic moduli of fibre-reinforced materials. J Appl Mech 31:223–232

    Article  Google Scholar 

  7. Singh B, Singh SJ (2004) Reflection of planes waves at the free surface of a fibre-reinforced elastic half-space. Sãdhanã 29:249–257

    MATH  Google Scholar 

  8. Chattopadhyay A, Choudhury S (1990) Propagation, reflection and transmission of magneto-elastic shear waves in a self-reinforced medium. Int J Eng Sci 28:485–495

    Article  MATH  Google Scholar 

  9. Chaudhary S, Kaushik VP, Tomar SK (2004) Reflection/transmission of plane wave through a self-reinforced elastic layer between two half-spaces. Acta Geophys Polon 52:219–235

    Google Scholar 

  10. Chattopadhyay A, Chaudhary S (1995) Magnetoelastic shear waves in an infinite self-reinforced plate. Int J Numer Anal Methods Geomech 19:289–304

    Article  MATH  Google Scholar 

  11. Pradhan A, Samal SK, Mahanti NC (2003) Influence of anisotropy on the love waves in a self-reinforced medium. Tamkang J Sci Eng 6(3):173–178

    Google Scholar 

  12. Chattopadhyay A, Venkateswarlu RLK, Saha S (2002) Reflection of quasi-P and quasi-SV waves at the free and rigid boundaries of a fibre-reinforced medium. Sãdhanã 27:613–630

    Google Scholar 

  13. Lord HW, Şhulman Y (1967) A generalized dynamical theory of thermo-elasticity. J Mech Phys Solids 15:299–306

    Article  ADS  MATH  Google Scholar 

  14. Green AE, Lindsay KA (1972) Thermoelasticity. J Elast 2:1–7

    Article  MATH  Google Scholar 

  15. Datta BK (1986) Some observation on interactions of Rayleigh waves in an elastic solid medium with the gravity field. Rev Roum Sci Tech, Sér Méc Appl 31(4):369–374

    Google Scholar 

  16. Das SC, Acharya DP, Sengupta PR (1992) Surface waves in an inhomogeneous elastic medium under the influence of gravity. Rev Roum Sci Tech, Sér Méc Appl 37(5):539–552

    MATH  MathSciNet  Google Scholar 

  17. Elnagar AM, Abd-Alla AM, Ahmed SM (1994) Rayleigh waves in a magneto-elastic initially stresses conducting medium with the gravity field. Bull Calcutta Math Soc 86:51–56

    Google Scholar 

  18. Abd-Alla AM (1999) Propagation of Rayleigh waves in an elastic half-space of orthotropic material. Appl Math Comput 99:61–69

    Article  MATH  MathSciNet  Google Scholar 

  19. Roychoudhuri SK, Banerjee M (2004) Magneto-elastic plane waves in rotating media in thermoelasticity of type II (G-N Model). Int J Math Math Sci 71:3917–3929

    Article  MathSciNet  Google Scholar 

  20. Green AE, Naghdi PM (1992) On undamped heat waves in an elastic solid. J Therm Stresses 15:253–264

    Article  ADS  MathSciNet  Google Scholar 

  21. Green AE, Naghdi PM (1993) Thermoelasticity without energy dissipation. J Elast 31:189–209

    Article  MATH  MathSciNet  Google Scholar 

  22. Othman MIA, Song YQ (2007) Reflection of plane waves from an elastic solid half-space under hydrostatic initial stress without energy dissipation. Int J Solids Struct 44:5651–5664

    Article  MATH  Google Scholar 

  23. Othman MIA, Atwa SY, Farouk RM (2008) Generalized magneto-thermovisco-elastic plane waves under the effect of rotation without energy dissipation. Int J Eng Sci 46:639–653

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Science, Department of Mathematics, Zagazig University, P.O. Box 44519, Zagazig, Egypt

    Mohamed I. A. Othman

  2. Higher Institute of Engineering, Department of Engineering Mathematics and Physics, Shorouk Academy, Shorouk City, Egypt

    Sarhan Y. Atwa

Authors
  1. Mohamed I. A. Othman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sarhan Y. Atwa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohamed I. A. Othman.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Othman, M.I.A., Atwa, S.Y. Effect of rotation on a fiber-reinforced thermo-elastic under Green-Naghdi theory and influence of gravity. Meccanica 49, 23–36 (2014). https://doi.org/10.1007/s11012-013-9748-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-013-9748-1

Keywords

Search

Navigation