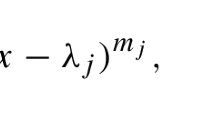Abstract
We consider the Ruelle zeta function R(s) of a genus g hyperbolic Riemann surface with n punctures and v ramification points. R(s) is equal to \(Z(s)/Z(s+1)\), where Z(s) is the Selberg zeta function. The main result of this work is the leading behavior of R(s) at \(s=0\). If \(n_0\) is the order of the determinant of the scattering matrix \(\varphi (s)\) at \(s=0\), we find that
which says that R(s) has order \(2g-2+n-n_0\) at \(s=0\), and its leading coefficient can be expressed in terms of \(m_1\), \(m_2\), \(\ldots \), \(m_v\), the ramification indices at the ramification points, and \({\tilde{\varphi }}(0)\), the leading coefficient of \(\varphi (s)\) at \(s=0\). The constant A is an even integer, equal to twice the multiplicity of the eigenvalue \(-\,1\) in the scattering matrix \(\Phi (s)\) at \(s=1/2\), and \((-1)^{\frac{A}{2}}=\varphi \left( \frac{1}{2}\right) \). We also consider the order of the Ruelle zeta function at other integers.
Similar content being viewed by others
References
Alekseevskii, V.P.: On functions similar to the gamma function. In: Communications and Proceedings of the Kharkov Mathematical Society, vol. 1, pp. 169–238 (1889) (Russian)
Barnes, E.W.: The theory of the \(G\)-function. Q. J. Math. 31, 264–314 (1900)
D’Hoker, E., Phong, D.H.: On determinants of Laplacians on Riemann surfaces. Commun. Math. Phys. 104, 537–545 (1986)
Dyatlov, S., Zworski, M.: Ruelle zeta function at zero for surfaces. Invent. Math. 210, 211–229 (2017)
Efrat, I.: Determinants of Laplacians on surfaces of finite volume. Commun. Math. Phys. 119, 443–451 (1988) Erratum: Commun. Math. Phys. 138, 607 (1991)
Fischer, J.: An approach to the Selberg trace formula via the Selberg zeta function. Lecture Notes in Mathematics, vol. 1253. Springer (1987)
Fried, D.: The zeta functions of Ruelle and Selberg. I. Ann. Sci. EcoleNorm. Sup. 19, 491–517 (1986)
Fried, D.: Analytic torsion and closed geodesics on hyperbolic manifolds. Invent. Math. 84, 523–540 (1986)
Fried, D.: Fuchsian groups and Reidemeister torsion. In: The Selberg Trace Formula and Related Topics, Brunswick, Maine, 1984. In: Contemp. Math., vol. 53. American Mathematical Society, Providence, RI, pp. 141–163 (1986)
Gon, Y.: Gamma factors of Selberg zeta functions and functional equation of Ruelle zeta functions. Math. Ann. 308, 251–278 (1997)
Gon, Y.: Differences of the Selberg trace formula and Selberg type zeta functions for Hilbert modular surfaces. J. Number Theory 147, 396–453 (2015)
Gon, Y., Park, J.: Ruelle zeta function for odd dimensional hyperbolic manifolds with cusps. Proc. Jpn. Acad. Ser. A Math. Sci. 84, 1–4 (2008)
Gon, Y., Park, I.: The zeta functions of Ruelle and Selberg for hyperbolic manifolds with cusps. Math. Ann. 346, 719–767 (2010)
Gong, D.: Zeta-determinant and torsion functions on Riemann surfaces of finite volume. Manuscr. Math. 86, 435–454 (1995)
Gradshteyn, I.S., Ryzhik, L.M.: Table of Integrals, Series and Products. Academic Press, Cambridge (2000)
Hejhal, D.: The Selberg trace formula for PSL(2, \({\mathbb{R}}\)). Lecture Notes in Mathematics, vol. 548. Springer (1976)
Hejhal, D.: The Selberg trace formula for PSL(2, \({\mathbb{R}}\)). Lecture Notes in Mathematics, vol. 1001. Springer (1983)
Iwaniec, H.: Spectral Methods of Automorphic Forms. American Mathematical Society, Providence (2002)
Koyama, S.-Y.: Determinant expression of Selberg zeta functions (I). Trans. Am. Math. Soc. 324, 149–168 (1991)
Koyama, S.-Y.: Determinant expression of Selberg zeta functions (III). Proc. Am. Math. Soc. 113, 303–311 (1991)
Momeni, A., Venkov, A.: Zeta functions and regularized determinants related to the Selberg trace formula. arXiv:1108.5659
Park, J.: Analytic torsion and Ruelle zeta functions for hyperbolic manifolds with cusps. J. Funct. Anal. 257, 1713–1758 (2009)
Ruelle, D.: Zeta-functions for expanding maps and Anosov flows. Invent. Math. 34, 231–242 (1976)
Sarnak, P.: Determinants of Laplacians. Commun. Math. Phys. 110, 113–120 (1987)
Selberg, A.: Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series. J. Indian. Math. Soc. B 20, 47–87 (1956)
Takhtajan, L.A., Zograf, P.G.: A local index theorem for families of \({\bar{\partial }}\)-operators on punctured Riemann surfaces and a new Kähler metric on their moduli spaces. Commun. Math. Phys. 137, 399–426 (1991)
Takhtajan, L.A., Zograf, P.: Local index theorem for orbifold Riemann surfaces. Lett. Math. Phys. 109, 1119–1143 (2019)
Venkov, A.B., Kalinin V.L., Faddeev, L.D.: A nonarithmetic derivation of the Selberg trace formula. J. Soviet Math. 8, 177–199 (1977). Translated from Zapiski Nauchnykh Seminarov Leningradskogo OtdeleniyaMatematicheskogo Instituta im. Vo A. Steklova AN SSSR 37, 5–42 (1973)
Venkov, A.B.: Spectral theory of automorphic functions. Proc. Steklov Inst. Math. 153, 1–163 (1982)
Voros, A.: Spectral functions, special functions and the Selberg zeta function. Commun. Math. Phys. 110, 439–465 (1987)
Acknowledgements
This work is supported by the Ministry of Education of Malaysia under FRGS Grant FRGS/1/2018/STG06/XMU/01/1. We would also like to thank L. Takhtajan and J. Friedman who have given helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Teo, LP. Ruelle zeta function for cofinite hyperbolic Riemann surfaces with ramification points. Lett Math Phys 110, 61–82 (2020). https://doi.org/10.1007/s11005-019-01222-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-019-01222-7
Keywords
- Ruelle zeta function
- Determinant of Laplacian
- Selberg zeta function
- Hyperbolic surfaces
- Cofinite Fuchsian groups