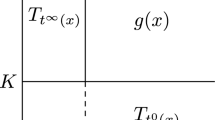Abstract
We consider Toeplitz operators defined on a concave corner-shaped subset of the square lattice. We obtain a necessary and sufficient condition for these operators to be Fredholm. We further construct a Fredholm concave corner Toeplitz operator of index one. By using this, a relation between Fredholm indices of quarter-plane and concave corner Toeplitz operators is clarified. As an application, topological invariants and corner states for some bulk-edges gapped Hamiltonians on two-dimensional (2-D) class AIII and 3-D class A systems with concave corners are studied. Explicit examples clarify that these topological invariants depend on the shape of the system. We discuss the Benalcazar–Bernevig–Hughes’ 2-D Hamiltonian and see that there still exist topologically protected corner states even if we break some symmetries as long as the chiral symmetry is preserved.






Similar content being viewed by others
Notes
The square lattice \(\mathbb {Z}^2\) is naturally embedded in the Euclidean space \(\mathbb {R}^2\). As a subset of \(\mathbb {R}^2\), what we called convex corners are not convex sets. We here use the words convex and concave just to distinguish the two models of corners indicated in Fig. 1.
In order to distinguish these two cases, we use hat “\(\wedge \)” for objects associated with convex corners and check “\(\vee \)” for those with concave corners (e.g., \(\hat{\mathcal {H}}^{\alpha ,\beta }\) and \(\check{\mathcal {H}}^{\alpha ,\beta }\)).
In what follows, K-groups of \(C^*\)-algebras \(\check{\mathcal {T}}^{\alpha ,\beta }\) and \(\check{\mathcal {C}}^{\alpha ,\beta }\) are computed, and the results for \(\mathcal {S}^{\alpha , \beta }\), \(\mathcal {C}^\alpha \) and \(\mathcal {C}^\beta \) are presented corresponding to the values of \(\alpha \) and \(\beta \). The case of \(\alpha = -\infty \) or \(\beta = + \infty \) is the same as that of rational \(\alpha \) or rational \(\beta \).
If A is an algebra, \(M_r(A)\) denotes the algebra of all \(r \times r\) matrices with entries in A.
\(P^{\alpha }h P^{\alpha }/|P^{\alpha }h P^{\alpha }|\) is defined by the continuous functional calculus by the continuous function \(\mathbb {C}\setminus \{ 0\} \rightarrow \mathbb {C}\) given by \(z \mapsto z/|z|\).
This element does not depend on the choice of the identification \(V \cong \mathbb {C}^N\).
We here give the definition of edge topological invariants for 1-D class AIII topological insulators. By the bulk-edge correspondence, this coincides with the bulk topological invariant which is defined as the winding number of the determinant of its symbol, that is \(\mathrm {Wind}(\{\det h_j(t)\}_{t \in \mathbb {T}})\) where \(H_j = \begin{pmatrix} 0 &{} h_j^*\\ h_j &{} 0 \end{pmatrix}\). (see [23], for example).
We here regard \(\mathbb {T}\) as the unit circle in the complex plane and fix the counterclockwise orientation.
\( \sigma _1 = \begin{pmatrix} 0 &{}\quad 1\\ 1 &{}\quad 0 \end{pmatrix}, \ \sigma _2 = \begin{pmatrix} 0 &{}\quad -i\\ i &{}\quad 0 \end{pmatrix}, \ \sigma _3 = \begin{pmatrix} 1 &{}\quad 0\\ 0 &{}\quad -1 \end{pmatrix}. \)
We here employ the following identification: \( \begin{pmatrix} a &{} b\\ c &{} d \end{pmatrix} \otimes A = \begin{pmatrix} aA &{} bA\\ cA &{} dA \end{pmatrix}. \)
Note that \(r_4 (\sigma _2 \otimes 1) r_4^* = - \sigma _3 \otimes \sigma _2\), \(r_4(\sigma _1 \otimes 1)r_4^* = \sigma _3 \otimes \sigma _1\), \( r_4(\sigma _3 \otimes \sigma _1)r_4^* = \sigma _1 \otimes 1\) and \(r_4 (\sigma _3 \otimes \sigma _2) r_4^* = \sigma _2 \otimes 1\) holds.
Note that we have \(U(\sigma _1 \otimes 1) U^* = \sigma _1 \otimes 1\), \(U(\sigma _2 \otimes 1) U^* = - \sigma _2 \otimes \sigma _3\), \(U(\sigma _3 \otimes \sigma _1) U^* = - \sigma _2 \otimes \sigma _2\) and \(U(\sigma _3 \otimes \sigma _2) U^* = - \sigma _2 \otimes \sigma _1\).
Specifically, they are \(U \varTheta U^* = \varTheta \), \(U \varXi U^* = (\sigma _3 \otimes \sigma _1) \circ \varTheta \), \(U \varPi U^* = \sigma _3 \otimes \sigma _1\), \(U m_x U^* = \sigma _1 \otimes \sigma _3\), \(U m_y U^* = \sigma _1 \otimes \sigma _1\) and \(U r_4 U^* = \begin{pmatrix} 0 &{}\quad 1 \\ -i\sigma _2 &{}\quad 0 \end{pmatrix}\), respectively.
References
Benalcazar, W.A., Bernevig, B.A., Hughes, T.L.: Quantized electric multipole insulators. Science 357, 61–66 (2017)
Blackadar, B.: \(K\)-Theory for Operator Algebras. Mathematical Sciences Research Institute Publications, vol. 5, 2nd edn. Cambridge University Press, Cambridge (1998)
Böttcher, A., Silbermann, B.: Analysis of Toeplitz operators. Springer Monographs in Mathematics, 2nd edn. Springer, Berlin (2006)
Bellissard, J., van Elst, A., Schulz-Baldes, H.: The noncommutative geometry of the quantum Hall effect. J. Math. Phys. 35(10), 5373–5451 (1994)
Coburn, L.A., Douglas, R.G.: \(C^{\ast } \)-algebras of operators on a half-space. I. Publ. Math. Inst. Hautes Études Sci. 40, 59–67 (1971)
Coburn, L.A., Douglas, R.G., Singer, I.M.: An index theorem for Wiener–Hopf operators on the discrete quarter-plane. J. Differ. Geom. 6, 587–593 (1972)
Connes, A.: Noncommutative Geometry. Academic Press Inc, San Diego (1994)
Cuntz, J.: Semigroup \(C^*\)-algebras and toric varieties. In: Cuntz, J., Echterhoff, S., Li, X., Yu, G. (eds.) \(K\)-Theory for Group \(C^*\)-Algebras and Semigroup \(C^*\)-Algebras. Oberwolfach Seminars, vol. 47, pp. 297–306. Birkhäuser, Basel (2017)
Douglas, R.G., Howe, R.: On the \(C^*\)-algebra of Toeplitz operators on the quarterplane. Trans. Am. Math. Soc. 158, 203–217 (1971)
Douglas, R.G.: Banach algebra techniques in the theory of Toeplitz operators. In: CBMS Regional Conference Series in Mathematics, no. 15. American Mathematical Society, Providence (1973)
Hatsugai, Y.: Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 71(22), 3697–3700 (1993)
Hatsugai, Y., Fukui, T.: Entanglement polarization for the topological quadrupole phase. Phys. Rev. B 98, 035147 (2018)
Hayashi, S.: Topological invariants and corner states for Hamiltonians on a three-dimensional lattice. Commun. Math. Phys. 364, 343–356 (2018)
Higson, N., Roe, J.: Analytic \(K\)-Homology. Oxford Mathematical Monographs. Oxford University Press, Oxford (2000)
Hardy, G.H., Wright, E.M.: An Introduction to the Theory of Numbers, 6th edn. Oxford University Press, Oxford (2008)
Hashimoto, L., Wu, X., Kimura, T.: Edge states at an intersection of edges of a topological material. Phys. Rev. B 95, 165443 (2017)
Jiang, X.: On Fredholm operators in quarter-plane Toeplitz algebras. Proc. Am. Math. Soc. 123(9), 2823–2830 (1995)
Ji, R., Kaminker, J.: The \(K\)-theory of Toeplitz extensions. J. Oper. Theory 19(2), 347–354 (1988)
Kellendonk, J., Richter, T., Schulz-Baldes, H.: Edge current channels and Chern numbers in the integer quantum Hall effect. Rev. Math. Phys. 14(1), 87–119 (2002)
Murphy, G.J.: \(C^*\)-Algebras and Operator Theory. Academic Press Inc, Boston (1990)
Park, E.: Index theory and Toeplitz algebras on certain cones in \({ Z}^2\). Oper. Theory 23(1), 125–146 (1990)
Peterson, C.W., Benalcazar, W.A., Hughes, T.L., Gaurav, B.: A quantized microwave quadrupole insulator with topologically protected corner states. Nature 555, 346–350 (2018)
Prodan, E., Schulz-Baldes, H.: Bulk and Boundary Invariants for Complex Topological Insulators. Mathematical Physics Studies. Springer, Berlin (2016)
Rørdam, M., Larsen, F., Laustsen, N.: An Introduction to \(K\)-Theory for \(C^*\)-Algebras. London Mathematical Society Student Texts, vol. 49. Cambridge University Press, Cambridge (2000)
Serra-Gracia, M., Peri, V., Süsstrunk, R., Bilal, O.R., Larsen, T., Villanueva, L.G., Huber, S.D.: Observation of a phononic quadrupole topological insulator. Nature 555, 342–345 (2018)
Schulz-Baldes, H., Kellendonk, J., Richter, T.: Simultaneous quantization of edge and bulk Hall conductivity. J. Phys. A 33(2), L27–L32 (2000)
Schindler, F., Cook, A.M., Vergniory, M.G., Wang, Z., Parkin, S.S., Bernevig, B.A., Neupert, T.: Higher-order topological insulators. Sci. Adv. 4(6), eaat0346 (2018)
Simonenko, I.B.: Convolution type operators in cones. Mat. Sb. 74(116), 298–313 (1967)
Thouless, D.J., Kohmoto, M., Nightingale, M.P., den Nijs, M.: Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982)
Xia, J.: The \(K\)-theory and the invertibility of almost periodic Toeplitz operators. Integral Equ. Oper. Theory 11(2), 267–286 (1988)
Acknowledgements
The author would like to thank Takeshi Nakanishi and Yukinori Yoshimura for showing him the result of a numerical calculation, which convinced him about the content of this paper. He also would like to thank Ken-Ichiro Imura and Ryo Okugawa for many discussions concerning [1] and Max Lein for sharing the information regarding [25]. The author acknowledges the support of the Erwin Schrödinger Institute where part of this work was conducted. He would like to thank organizers of the workshop “Bivariant K-theory in Geometry and Physics” for their hospitability. This work was supported by JSPS KAKENHI Grant Nos. JP17H06461 and JP19K14545.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A some variants
A some variants
As in Remark 1, most results in this paper also hold in the cases in which the corners (or edges) do not necessarily include lattice points on lines \(y=\alpha x\) and \(y=\beta x\). In this appendix, we make this statement precise by fixing the setups and clarifying the corresponding results. Although the proofs of the corresponding results are parallel with those contained in the main body of this paper, some parts of the discussions are based on the explicit construction of an example, especially the constructions of rank-one projections (Lemma 2), and that of the Fredholm concave corner Toeplitz operator of index one (Theorem 3). For these reasons, we collect the corresponding results in this appendix. The corresponding results for quarter-plane Toeplitz operators, briefly mentioned in [17], are also included for completeness.
Since we consider two edges, corresponding to whether the edge includes lattice points on boundaries, we can consider four cases. Each case corresponds to the case in which closed subspaces \(\mathcal {H}^{\alpha }\) and \(\mathcal {H}^{\beta }\) of \(\mathcal {H}\) are spanned by the following sets:
-
Case 1 : \(\{ { e_{m,n}} \mid -\alpha m + n \ge 0 \}\) and \(\{ { e_{m,n}} \mid -\beta m + n \le 0 \}\), respectively.
-
Case 2 : \(\{ { e_{m,n}} \mid -\alpha m + n > 0 \}\) and \(\{ { e_{m,n}} \mid -\beta m + n \le 0 \}\), respectively.
-
Case 3 : \(\{ { e_{m,n}} \mid -\alpha m + n \ge 0 \}\) and \(\{ { e_{m,n}} \mid -\beta m + n < 0 \}\), respectively.
-
Case 4 : \(\{ { e_{m,n}} \mid -\alpha m + n > 0 \}\) and \(\{ { e_{m,n}} \mid -\beta m + n < 0 \}\), respectively.
For these cases, we associate concave corners and define concave corner \(C^*\)-algebras \(\check{\mathcal {T}}^{\alpha ,\beta }\) in the same way as in Sect. 2. Note that Case 1 is already treated in the main body of this paper. In the following, we assume the condition (\(\dagger \)) for \(\alpha \) and \(\beta \).
We first collect constructions of rank-one projections in Cases 2–4. They correspond to Lemma 2 in Case 1. As in Lemma 2, we take \(N \in \{ 2,3,\ldots \}\) such that \(\frac{1}{N+1} < \alpha \le \frac{1}{N}\).
Lemma 4
In Case 2–4, some \(\tilde{\mathcal {P}}_k\) is a rank-one projection. Explicitly, we have the following results.
In Case 2, \({\left\{ \begin{array}{ll} \text {when} \ \frac{1}{N+1}< \alpha \le \frac{1}{N} \ \text {and} \ \beta = 1, \text {we have} \ \tilde{\mathcal {P}}_{N-1} = p_{-N-1,-1}.\\ \text {when} \ \frac{1}{N+1}< \alpha \le \frac{1}{N} \ \text {and} \ 1< \beta < \infty , \text {we have} \ \tilde{\mathcal {P}}_N = p_{-N-1,-1}. \end{array}\right. }\)
In Case 3, \({\left\{ \begin{array}{ll} \text {when} \ \alpha = \frac{1}{N} \ \text {and} \ 1< \beta \le \infty , \ \text {we have} \ \tilde{\mathcal {P}}_{N-1} = p_{-N,-1}.\\ \text {when} \ \frac{1}{N+1}< \alpha< \frac{1}{N} \ \text {and} \ 1 < \beta \le \infty , \text {we have} \ \tilde{\mathcal {P}}_N = p_{-N-1,-1}. \end{array}\right. }\)
In Case 4, \({\left\{ \begin{array}{ll} \text {when} \ \alpha = \frac{1}{N} \ \text {and} \ \beta = 1, \ \text {we have} \ \tilde{\mathcal {P}}_{1} = p_{-1,0}.\\ \text {in the other cases (under } (\dagger )), \text { we have} \ \tilde{\mathcal {P}}_{N} = p_{-N-1,-1}. \end{array}\right. }\)
We here write down the result of computing the Fredholm index of the following operator in Cases 2–4 which corresponds to Theorem 3 in Case 1.
Proposition 6
In Cases 2–4, \(\check{A}\) is a surjective Fredholm operator whose Fredholm index is 1. We also have \(\check{A} - 1 \in \check{\mathcal {C}}^{\alpha ,\beta }\). Its kernel is given as follows:
In Case 2, \({\left\{ \begin{array}{ll} \text {when} \ 0< \alpha \le \frac{1}{2} \ \text {and} \ \beta = 1, {\mathrm {Ker}}\check{A} = \mathbb {C}({\varvec{e}}_{-2, 0} - {\varvec{e}}_{-1,0}).\\ \text {when} \ 0< \alpha \le \frac{1}{2} \ \text {and} \ 1< \beta < \infty , {\mathrm {Ker}}\check{A} = \mathbb {C}({\varvec{e}}_{-1,0} - {\varvec{e}}_{0,0}). \end{array}\right. }\)
In Case 3, under the assumption \((\dagger )\), we have \({\mathrm {Ker}}\check{A} = \mathbb {C}({\varvec{e}}_{-1,0} - {\varvec{e}}_{0,0})\).
In Case 4, under the assumption \((\dagger )\), we have \({\mathrm {Ker}}\check{A} = \mathbb {C}({\varvec{e}}_{0,1} - {\varvec{e}}_{1,1})\).
We next consider the following quarter-plane Toeplitz operator in Cases 1–4.
Note that \(\hat{A} \in \hat{\mathcal {T}}^{\alpha ,\beta }\). Jiang shows in [17] that, under the assumption (\(\dagger \)), this is an isometric Fredholm operator and compute its Fredholm index mainly in the Case 1. The other cases are briefly mentioned (Remark (1) in p2828 of [17]), though their Fredholm indices are stated as \(\pm 1\). We here need to fix its sign in order to obtain the corresponding result for Corollary 1 especially in Cases 2–4. For this reason, we (re)state necessary results in the following. Its proof is totally parallel with that of Jiang [17].
Proposition 7
(Jiang [17]) In Cases 1–4, \(\hat{A}\) is an isometric Fredholm operator whose Fredholm index is \(-1\). Its cokernel is given as follows:
In Case 1, under the assumption \((\dagger )\), we have \({\mathrm {Coker}}\hat{A} = \mathbb {C}{\varvec{e}}_{0,0}\).
In Case 2, under the assumption \((\dagger )\), we have \({\mathrm {Coker}}\hat{A} = \mathbb {C}{\varvec{e}}_{1,1}\).
In Case 3, \({\left\{ \begin{array}{ll} \text {when} \ 0< \alpha \le \frac{1}{2} \ \text {and} \ \beta = 1, {\mathrm {Coker}}\hat{A} = \mathbb {C}{\varvec{e}}_{2,1}.\\ \text {when} \ 0< \alpha \le \frac{1}{2} \ \text {and} \ 1< \beta < \infty , {\mathrm {Coker}}\hat{A} = \mathbb {C}{\varvec{e}}_{1,1}. \end{array}\right. }\)
In Case 4, \({\left\{ \begin{array}{ll} \text {when} \ \alpha = \frac{1}{2} \ \text {and} \ \beta = 1, {\mathrm {Coker}}\hat{A} = \mathbb {C}{\varvec{e}}_{3,2}.\\ \text {when} \ 0< \alpha< \frac{1}{2} \ \text {and} \ \beta = 1, {\mathrm {Coker}}\hat{A} = \mathbb {C}{\varvec{e}}_{2,1}.\\ \text {when} \ 0< \alpha \le \frac{1}{2} \ \text {and} \ 1< \beta < \infty , {\mathrm {Coker}}\hat{A} = \mathbb {C}{\varvec{e}}_{1,1}. \end{array}\right. }\)
Rights and permissions
About this article
Cite this article
Hayashi, S. Toeplitz operators on concave corners and topologically protected corner states. Lett Math Phys 109, 2223–2254 (2019). https://doi.org/10.1007/s11005-019-01184-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-019-01184-w
Keywords
- Toeplitz operators on concave corners
- Topologically protected corner states
- Bulk-edge and corner correspondence
- K-theory and index theory