Generating series for GUE correlators

Abstract

We extend to the Toda lattice hierarchy the approach of Bertola et al. (Phys D Nonlinear Phenom 327:30–57, 2016; IMRN, 2016) to computation of logarithmic derivatives of tau-functions in terms of the so-called matrix resolvents of the corresponding difference Lax operator. As a particular application we obtain explicit generating series for connected GUE correlators. On this basis an efficient recursive procedure for computing the correlators in full genera is developed.

A Appendix: GUE, Toda lattice, and enumeration of ribbon graphs

1.1 A.1 GUE partition function and orthogonal polynomials

Consider the GUE partition function represented as an integral over the space ${\mathcal H}(N)$ of $N\times N$ Hermitian matrices $M=\left( M_{ij}\right)$

$$\begin{aligned} Z_N(\mathbf{s}; \epsilon )=\frac{(2\pi )^{-{N}} \epsilon ^{-\frac{1}{12}}}{\mathrm{Vol}(N)} \int _{{\mathcal H}(N)} e^{-\frac{1}{\epsilon } \mathrm{tr}\,V(M)} \mathrm{d}M. \end{aligned}$$

(A.1.1)

Here the formal series V depending on the parameters $\mathbf{s}=(s_1,s_2,s_3, \ldots )$ has the form

$$\begin{aligned} V(M)=\frac{1}{2} M^2 - \sum _{j\ge 1} s_j M^j. \end{aligned}$$

(A.1.2)

The integral with respect to the measure

$$\begin{aligned} \mathrm{d}M=\prod _{i=1}^N \mathrm{d}M_{ii} \prod _{i<j} \mathrm{d}\mathrm{Re}( M_{ij})\, \mathrm{d}\mathrm{Im}(M_{ij}) \end{aligned}$$

will be understood as a formal series⁴ with respect to the parameters $s_j$. The prefactor $\mathrm{Vol}(N)^{-1}$ corresponds to the volume, with respect to the Haar measure, of the quotient of the unitary group over the maximal torus $\left[ U(1)\right] ^N$

$$\begin{aligned} \mathrm{Vol}(N)=\mathrm{Vol} \left( U(N)/\left[ U(1)\right] ^N\right) =\frac{\pi ^{\frac{N(N-1)}{2}} }{G(N+1)} \end{aligned}$$

(A.1.3)

Here G is the Barnes G-function taking the value

$$\begin{aligned} G(N+1)=\prod _{n=1}^{N-1} n! \end{aligned}$$

(A.1.4)

at positive integers. Formula (A.1.3) will be re-derived below.

Denote ${\mathcal D}_N$ the set of diagonal $N\times N$ matrices $\Lambda =\mathrm{diag}(\lambda _1, \lambda _2, \ldots , \lambda _N)$ with real ordered eigenvalues $\lambda _1\le \lambda _2\le \cdots \le \lambda _N$. The map

$$\begin{aligned}&U(N)/\left[ U(1)\right] ^N\times {\mathcal D}_N\rightarrow {\mathcal H}(N) \nonumber \\&\left( U, \Lambda \right) \mapsto U\,\Lambda \, U^* \end{aligned}$$

(A.1.5)

is a local diffeomorphism away from a subset of codimension three in ${\mathcal H}(N)$. Because of invariance of the measure w.r.t. to the action of unitary group one obtains

$$\begin{aligned} \int _{{\mathcal H}(N)} e^{-\frac{1}{\epsilon } \mathrm{tr}\,V(M)} \mathrm{d}M=\mathrm{Vol}\left( U(N)/\left[ U(1)\right] ^N\right) \int _{{\mathcal D}_N}\!\varDelta ^2(\lambda ) \, e^{-\frac{1}{\epsilon } \sum _{k=1}^N V(\lambda _k)}\mathrm{d}\lambda _1\cdots \mathrm{d}\lambda _N. \end{aligned}$$

Here

$$\begin{aligned} \varDelta (\lambda )=\prod _{i<j} (\lambda _i-\lambda _j) \end{aligned}$$

is the Vandermonde determinant. Due to symmetry of the integrand one can rewrite the last formula as

$$\begin{aligned} \int _{{\mathcal H}(N)} e^{-\frac{1}{\epsilon } \mathrm{tr}\,V(M)} \mathrm{d}M=\frac{1}{N!} \mathrm{Vol} \left( U(N)/\left[ U(1)\right] ^N\right) \int _{\mathbb R^N} \varDelta ^2(\lambda ) \, e^{-\frac{1}{\epsilon } \sum _{k=1}^N V(\lambda _k)}\mathrm{d}\lambda _1\cdots \mathrm{d}\lambda _N. \end{aligned}$$

Denote

$$\begin{aligned} p_n(\lambda )=\lambda ^n+a_{1n} \lambda ^{n-1}+\cdots +a_{nn}, \quad n=0,1, 2, \ldots \end{aligned}$$

(A.1.6)

a system of monic polynomials orthogonal w.r.t. to the exponential weight

$$\begin{aligned} \int _{-\infty }^\infty p_n(\lambda ) \, p_m(\lambda ) \, e^{-\frac{1}{\epsilon } V(\lambda )}\mathrm{d}\lambda =: h_n \, \delta _{mn}. \end{aligned}$$

(A.1.7)

Representing the Vandermonde as

$$\begin{aligned} \varDelta (\lambda )=\det \left( \begin{array}{cccc} p_0(\lambda _1) &{} p_0(\lambda _2) &{} \cdots &{} p_0(\lambda _N)\\ p_1(\lambda _1) &{} p_1(\lambda _2) &{} \cdots &{} p_1(\lambda _N)\\ \cdot &{} \cdot &{} \cdots &{} \cdot \\ \cdot &{} \cdot &{} \cdots &{} \cdot \\ \cdot &{} \cdot &{} \cdots &{} \cdot \\ p_{N-1}(\lambda _1) &{} p_{N-1}(\lambda _2) &{} \cdots &{} p_{N-1}(\lambda _N)\end{array}\right) \end{aligned}$$

one obtains an expression of the last integral via the normalizing factors of the orthogonal polynomials

$$\begin{aligned} \int _{\mathbb R^N} \varDelta ^2(\lambda ) e^{-\frac{1}{\epsilon } \sum _{k=1}^N V(\lambda _k)}\mathrm{d}\lambda _1\cdots \mathrm{d}\lambda _N=N! \,h_0 \, h_1\cdots h_{N-1}. \end{aligned}$$

We conclude that

$$\begin{aligned} \int _{{\mathcal H}(N)} e^{-\frac{1}{\epsilon } \mathrm{tr}\,V(M)} \mathrm{d}M=\mathrm{Vol} \left( U(N)/\left[ U(1)\right] ^N\right) \, h_0 \, h_1\cdots h_{N-1}. \end{aligned}$$

(A.1.8)

Formula (A.1.3) for the volume $\mathrm{Vol} \left( U(N)/\left[ U(1)\right] ^N\right)$ can be easily derived from the last equation. Indeed, evaluating the LHS of Eq. (A.1.8) at the Gaussian point $\mathbf{s}=0$ one obtains

$$\begin{aligned} \int _{{\mathcal H}(N)} e^{-\frac{1}{2\epsilon } \mathrm{tr}\, M^2} \mathrm{d}M=2^{\frac{N}{2}} \left( \pi \,\epsilon \right) ^{\frac{N^2}{2}}. \end{aligned}$$

At $\mathbf{s}=0$ the orthogonal polynomials (A.1.6)–(A.1.7) are expressed via Hermite polynomials

$$\begin{aligned} p_n(\lambda )=\epsilon ^{\frac{n}{2}}\, \mathrm{He}_n(x), \quad \lambda =\epsilon ^{\frac{1}{2}}x. \end{aligned}$$

From

$$\begin{aligned} \int _{-\infty }^\infty \mathrm{He}_n(x) \, \mathrm{He}_m(x) \, e^{-\frac{1}{2} x^2} \mathrm{d}x=\sqrt{2\pi } \,n! \,\delta _{mn} \end{aligned}$$

it follows that

$$\begin{aligned} h_n(\mathbf{s}=0)= \epsilon ^{n+\frac{1}{2}} \sqrt{2\pi } \,n! \end{aligned}$$

So, Eq. (A.1.8) at $\mathbf{s}=0$ takes the form

$$\begin{aligned} 2^{\frac{N}{2}} \left( \pi \,\epsilon \right) ^{\frac{N^2}{2}}= \mathrm{Vol} \left( U(N)/\left[ U(1)\right] ^N\right) \cdot \left( 2\pi \right) ^{\frac{N}{2}} \epsilon ^{\frac{N^2}{2}} \prod _{n=1}^{N-1} n! \end{aligned}$$

This implies (A.1.3).

We conclude this section with the following expression for the GUE partition function

$$\begin{aligned} Z_N(\mathbf{s}; \epsilon ) = h_0 \, h_1 \cdots h_{N-1}. \end{aligned}$$

(A.1.9)

Our nearest goal is to prove that this partition function is the tau-function of a particular solution of Toda hierarchy.

1.2 A.2 GUE and Toda

Denote $v_n$, $w_n$ the coefficients of the three-term recursion relation for the orthogonal polynomials $p_n(\lambda )$

$$\begin{aligned} \lambda \, p_n(\lambda ) =p_{n+1}(\lambda ) +v_n \, p_n(\lambda ) + w_n \, p_{n-1}(\lambda ), \quad n\ge 0 \end{aligned}$$

(A.2.1)

$p_{-1}=0$. That is, the orthogonal polynomials are eigenvectors of the second-order difference operator

$$\begin{aligned} \left( L\, \psi \right) _n = \psi _{n+1} +v_n \, \psi _n + w_n \, \psi _{n-1}. \end{aligned}$$

(A.2.2)

The corresponding tri-diagonal matrix will also be denoted $L=\left( L_{ij}\right)$.

Denote

$$\begin{aligned} (f, g)=\int _{-\infty }^\infty f(\lambda ) \, g(\lambda ) \, e^{-\frac{1}{\epsilon } V(\lambda )}\mathrm{d}\lambda \end{aligned}$$

(A.2.3)

an inner product on the space of polynomials. Recall that all integrals are understood as formal series in the $s_j$-variables. The symmetry

$$\begin{aligned} \left( \lambda \, p_n, p_m\right) =\left( p_n, \lambda \, p_m\right) ~\Leftrightarrow ~ L_{mn} h_m=L_{nm} h_n \end{aligned}$$

implies

$$\begin{aligned} w_n=\frac{h_n}{h_{n-1}}=\frac{Z_{n+1} Z_{n-1}}{Z_{n}^2}. \end{aligned}$$

(A.2.4)

Here $h_n=(p_n, p_n)$ [see Eq. (A.1.7)].

For an arbitrary square matrix $X=(X_{ij})$ denote $X_-$ and $X_+$ its upper- and lower-triangular parts

$$\begin{aligned} X_-=\left( X_{ij}\right) _{i<j}, \quad X_+=\left( X_{ij}\right) _{i\ge j}, \quad X=X_+ + X_-. \end{aligned}$$

Lemma A.2.1

The orthogonal polynomials $p_n=p_n(\lambda )$ satisfy

$$\begin{aligned} \epsilon \,\frac{\partial p_n}{\partial s_j} +(A_j \, p)_n=0, \quad A_j = -\left( L^{j} \right) _-, \quad j\ge 1. \end{aligned}$$

(A.2.5)

Proof

Write

$$\begin{aligned} \frac{\partial p_n(\lambda )}{\partial s_j} =\sum _{i=0}^{n-1} A_{i\, n}^{(j)} \, p_i(\lambda ), \quad n\ge 1 \end{aligned}$$

for some coefficients $A_{in}^{(j)}$. Differentiating in $s_j$ the equation $(p_n, p_m)=0$ for $m<n$ we obtain

$$\begin{aligned} A_{mn}^{(j)}h_m +\frac{1}{\epsilon } \left( \lambda ^{j} p_n, p_m\right) =0. \end{aligned}$$

Introduce matrices of multiplication by powers of $\lambda$

$$\begin{aligned} \lambda ^{j}p_n(\lambda )=\sum _{i=0}^{n+j} \left( L^{j}\right) _{in} p_i(\lambda ). \end{aligned}$$

(A.2.6)

We have

$$\begin{aligned} \left( \lambda ^{j}p_n, p_m\right) =\left( L^{j}\right) _{mn} h_m, \end{aligned}$$

hence

$$\begin{aligned} \epsilon \, A_{mn}^{(j)} =- \left( L^{j}\right) _{mn}, \quad m<n \end{aligned}$$

(A.2.7)

that is,

$$\begin{aligned} \epsilon \, A^{(j)}=- \left( L^{j}\right) _-. \end{aligned}$$

$\square$

Repeating a similar calculation for $m=n$ we obtain

$$\begin{aligned} \frac{\partial }{\partial s_j} \log \frac{Z_{n+1}}{Z_n} \equiv \frac{\partial }{\partial s_j}\log h_n = \left( L^{j} \right) _{nn}. \end{aligned}$$

(A.2.8)

Corollary A.2.2

The difference operator L satisfies

$$\begin{aligned} \epsilon \, \frac{\partial L}{\partial s_j} =\left[ A_j, L\right] , \quad A_j=\left( L^{j}\right) _+. \end{aligned}$$

(A.2.9)

Proof

Differentiating equation

$$\begin{aligned} \lambda \, p_n =\sum _{i=0}^{n+1} L_{in} \, p_i \end{aligned}$$

in $s_j$ and using Eq. (A.2.5) we obtain

$$\begin{aligned} \epsilon \, \frac{\partial L}{\partial s_j} =\left[ L, \left( L^{j}\right) _-\right] . \end{aligned}$$

Since the operators L and $L^{j}$ commute we arrive at (A.2.9). $\square$

Proposition A.2.3

The GUE partition function $Z_n$ is a tau-function, in the sense of Definition 1.2.4 of the Toda lattice hierarchy, where the time variables are defined by $t_j=s_{j+1}/\epsilon , ~j=0,1,2,\ldots$.

Proof

Cor. A.2.2 tells that $w_n,v_n$ is a particular solution to the Toda lattice hierarchy. It then follows from (A.2.4) and (A.2.8) that $Z_n$ satisfies Eqs. (1.2.9) and (1.2.10). Equation (A.2.8) implies that

$$\begin{aligned} \frac{\partial }{\partial t_{j}} \log \frac{Z_{n+1}}{Z_n} = (j+1)\, h_{j-1}(n), \quad j\ge 0 \end{aligned}$$

where $h_{j-1}(n):=\frac{1}{j+1} (L^{j+1})_{nn}$. Define

$$\begin{aligned} \gamma _n(\lambda )= \frac{1}{\lambda } + \sum _{j\ge 0} \frac{ (j+1)\, h_{j-1}(n-1)}{\lambda ^{j+2}}. \end{aligned}$$

We have

$$\begin{aligned} \sum _{j\ge 0}\frac{1}{\lambda ^{j+2}} \frac{\partial }{\partial t_{j}} \log \frac{Z_{n+1}}{Z_n} = \sum _{j\ge 0}\frac{1}{\lambda ^{j+2}} (j+1)\, h_{j-1}(n) = \gamma _{n+1}(\lambda )-\frac{1}{\lambda }. \end{aligned}$$

So

$$\begin{aligned} \sum _{i,j\ge 0}\frac{1}{\mu ^{i+2}\lambda ^{j+2}} \frac{\partial ^2}{\partial t_{j}\partial t_i} \log \frac{Z_{n+1}}{Z_n} = \nabla (\mu )\, \gamma _{n+1}(\lambda ). \end{aligned}$$

Here, $\nabla (\mu )$ is defined in (2.2.9). Noting that

$$\begin{aligned} \nabla (\mu )\, \gamma _{n+1}(\lambda )= & {} \frac{\gamma _{n+1}(\lambda )(1+2\alpha _{n+1}(\mu ))-\gamma _{n+1}(\mu )(1+2\alpha _{n+1}(\lambda ))}{\lambda -\mu }\\&+\gamma _{n+1}(\lambda )\gamma _{n+1}(\mu )\\= & {} \frac{\mathrm{tr}\, R_{n+1}(\lambda ) R_{n+1}(\mu ) - \mathrm{tr}\, R_n(\lambda ) R_n(\mu )}{(\lambda -\mu )^2} \end{aligned}$$

we obtain

$$\begin{aligned} \sum _{i,j\ge 0}\frac{1}{\mu ^{i+2}\lambda ^{j+2}} \frac{\partial ^2}{\partial t_{j}\partial t_i} \log Z_n = \frac{\mathrm{tr}\, R_n(\lambda ) R_n(\mu ) -1}{(\lambda -\mu )^2} . \end{aligned}$$

In the above formulae, $R_n$ is the matrix resolvent of L. The proposition is proved. $\square$

1.3 A.3 GUE and enumeration of ribbon graphs

Expanding in powers of $s_1$, $s_2$, $s_3$, ...

$$\begin{aligned} \int _{{\mathcal H}(N)} e^{-\frac{1}{\epsilon } \mathrm{tr}\,V(M)} \mathrm{d}M=\sum _{k\ge 0}\frac{\epsilon ^{-k}}{k!}\int _{{\mathcal H}(N)} e^{-\frac{1}{2\epsilon } \mathrm{tr}\, M^2}\sum _{i_1, \ldots , i_k} s_{i_1}\cdots s_{i_k} \mathrm{tr}\, M^{i_1} \cdots \mathrm{tr}\, M^{i_k} \,\mathrm{d}M \end{aligned}$$

and using an obvious formula

$$\begin{aligned} \frac{\int _{{\mathcal H}(N)} e^{-\frac{1}{2\epsilon } \mathrm{tr}\, M^2} \mathrm{tr}\, M^{i_1} \cdots \mathrm{tr}\, M^{i_k} \,\mathrm{d}M}{\int _{{\mathcal H}(N)} e^{-\frac{1}{2\epsilon } \mathrm{tr}\,M^2} \mathrm{d}M}=\epsilon ^{\frac{i_1+\cdots +i_k}{2}}\frac{\int _{{\mathcal H}(N)} e^{-\frac{1}{2} \mathrm{tr}\, M^2} \mathrm{tr}\, M^{i_1} \cdots \mathrm{tr}\, M^{i_k} \,\mathrm{d}M}{\int _{{\mathcal H}(N)} e^{-\frac{1}{2} \mathrm{tr}\,M^2} \mathrm{d}M} \end{aligned}$$

(note that both sides of this equation vanish if $i_1+\cdots +i_k=\,$odd) one obtains

$$\begin{aligned} \frac{Z_N(\mathbf{s}; \epsilon )}{Z_N(0; \epsilon )}= \sum _{m\in \mathbb Z} \epsilon ^m \sum _{ k\ge 0} \frac{1}{k!} \sum _{ i_1+\cdots +i_k= 2k+2 m} s_{i_1}\cdots s_{i_k} \left\langle \mathrm{tr}\, M^{i_1}\cdots \mathrm{tr}\, M^{i_k} \right\rangle \qquad \end{aligned}$$

(A.3.1)

where, as above

$$\begin{aligned} \left\langle \mathrm{tr}\, M^{i_1}\cdots \mathrm{tr}\, M^{i_k} \right\rangle :=\frac{\int \mathrm{tr}\, M^{i_1}\cdots \mathrm{tr}\, M^{i_k}\,e^{-\frac{1}{2} \mathrm{tr}\, M^2} \, \mathrm{d}M}{\int e^{-\frac{1}{2} \mathrm{tr}\, M^2}\mathrm{d}M}. \end{aligned}$$

(A.3.2)

The coefficients (A.3.2) of the perturbative expansion (A.3.1) are polynomials in N that can be computed by applying the Wick rule. For example,

$$\begin{aligned} \left\langle \mathrm{tr}\, M^4\right\rangle =2N^3+N, \quad \left\langle \left( \mathrm{tr}\, M^3\right) ^2\right\rangle =12 N^3 + 3 N, \quad \left\langle \mathrm{tr}\, M^6\right\rangle =5N^4 + 10 N^2 \end{aligned}$$

etc. Terms of polynomial (A.3.2) correspond to oriented ribbon graphs with k vertices. Expansion of the logarithm of the partition function has a similar structure keeping connected graphs only

$$\begin{aligned} \log \frac{Z_N(\mathbf{s}; \epsilon )}{Z_N(0; \epsilon )}= \sum _{m} \epsilon ^m \sum _{ k\ge 0} \frac{1}{k!} \, \sum _{ i_1+\cdots +i_k=2k+2 m} s_{i_1}\cdots s_{i_k} \left\langle \mathrm{tr}\, M^{i_1}\cdots \mathrm{tr}\, M^{i_k} \right\rangle _c.\nonumber \\ \end{aligned}$$

(A.3.3)

Introduce the ’t Hooft coupling parameter

$$\begin{aligned} x=N\, \epsilon . \end{aligned}$$

Re-expanding in $\epsilon$ the logarithm of the partition function we arrive at the main statement of this section, see [7].

Theorem A.3.1

Logarithm of the tau-function of the solution to the Toda hierarchy given by the GUE partition function has the following expansion

(A.3.4)

where $h=2-2g -\left( k-\frac{|i|}{2}\right) , |i|=i_1+\cdots + i_k$, and the last summation is taken over all connected ribbon graphs $\Gamma$ (with labelled half-edges and unlabelled vertices) of genus g with k vertices of valencies $i_1$, ..., $i_k$, and $\#\,\mathrm{Sym}\, \Gamma$ is the order of the symmetry group of $\Gamma$ generated by permuting the vertices.⁵

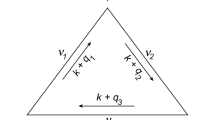
In the particular case $i_1=i_2=\cdots =i_k=3$ the dual to the ribbon graph is a triangulation of the surface of genus g consisting of k triangles. Thus, $a_g\!\left( 3^k\right) :=a_g(3, \ldots , 3)$ (k times) is equal to the weighted number of triangulations of genus g with k triangles. In a similar way, $a_g\!\left( 4^k\right)$ is the weighted number of quadrangulations of a surface of genus g with k squares, etc.

Since

$$\begin{aligned} Z_N(0; \epsilon )=(2\pi )^{-\frac{N}{2}} \epsilon ^{\frac{N^2}{2}-\frac{1}{12}}\, G(N+1) \end{aligned}$$

we can also expand the first term in (A.3.4) with the help of the asymptotic expansion of the Barnes G-function (cf. [2, 23, 37])

This yields the following genus expansion of the logarithm of the tau-function of the interpolated Toda hierarchy where the shift operator $\psi _n\mapsto \psi _{n+1}$ acting on functions on a lattice is replaced with the translation $\psi (x) \mapsto \psi (x+\epsilon )$ acting on smooth functions on the real line,

$$\begin{aligned} \log \tau (x; \mathbf{s};\epsilon )&= \frac{x^2}{2\epsilon ^2} \left( \log x -\frac{3}{2}\right) -\frac{1}{12} \log x +\zeta '(-1)\nonumber \\&\quad +\sum _{g\ge 2} \epsilon ^{2g-2} \frac{B_{2g}}{4g(g-1)x^{2g-2}} \nonumber \\&\quad +\sum _{g\ge 0} \epsilon ^{2g-2} \sum _{k\ge 0} \sum _{ i_1, \ldots , i_k} a_g(i_1, \ldots , i_k) \, s_{i_1} \cdots s_{i_k} x^{2-2g -\left( k-\frac{|i|}{2}\right) }. \end{aligned}$$

(A.3.6)

Remark A.3.2

The genus expansion (A.3.6) is often written as 1 / N expansion, setting $x=1$, so $\epsilon =1/N$,

$$\begin{aligned} \log Z_N(\mathbf{s}; N^{-1})&= \sum _{g\ge 0} N^{2-2g} \mathcal{F}_g (\mathbf{s}) \\ \mathcal{F}_g(\mathbf{s})&= - \delta _{g,0} \, \frac{3}{4} + \delta _{g,1} \, \zeta '(-1) +\delta _{g\ge 2} \, \frac{B_{2g}}{4g(g-1)}\\&\quad + \sum _{k\ge 0} \sum _{i_1, \ldots , i_k} a_g(i_1, \ldots , i_k) \, s_{i_1} \cdots s_{i_k}. \end{aligned}$$

The coefficients $a_g(i_1, \ldots , i_k)$ are the same as in (A.3.4).

Observe that the coefficients of the connected correlators as polynomials in N can be expressed via the numbers $a_g(i_1, \ldots , i_k)$ enumerating ribbon graphs. Namely, $\forall \,k\ge 1$ and $\forall \, i_1,\ldots ,i_k$ such that |i| is even, we have

$$\begin{aligned} \langle \mathrm{tr}\, M^{i_1} \, \mathrm{tr}\, M^{i_2} \, \cdots \, \mathrm{tr}\, M^{i_k} \rangle _c\,=\,k!\,\sum _{0\le g \le \frac{|i|}{4}-\frac{k}{2}+\frac{1}{2}} \, a_g(i_1,\ldots ,i_k) \, N^{2-2g-k+\frac{|i|}{2}}.\nonumber \\ \end{aligned}$$

(A.3.7)