Skip to main content
SpringerLink
Log in

Local Frictional Wear of an Elastic Half-Space with a Regular System of Protrusions

  • Published:
Materials Science Aims and scope

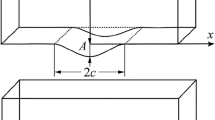
Wear-contact of two elastic half-planes (plain deformation), the surface of one has periodic sloping protrusions of cylindrical shape under local wear on the basis of the frictional-fatigue fracture model is investigated. The formulated contact problem is reduced to a singular integro-differential equation with a Hilbert nucleus with respect to the thickness of the worn material and equations for determining the unknown areas of wear. The shape of the protrusions and contact pressure at the beginning and after wear are analyzed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. I. Etsion, “State of the art in laser surface texturing,” J. of Tribology, 127, Is. 1, 248–253 (2005); https://doi.org/10.1115/1.1828070.

  2. P. Stepien, “Deterministic and stochastic components of regular surface texture generated by a special grinding process,” Wear, 271, Iss. 3–4, 514–518 (2011); https://doi.org/https://doi.org/10.1016/j.wear.2010.03.027.

    Article  CAS  Google Scholar 

  3. B. A. Lyashenko, N. V. Novokov, and S. A. Klimenko, Discrete modification of the Surface Layer of Machine Elements and Tools [in Russian], Kyiv, Bakul Institute of Superhard Materials (2017).

  4. V. M. Aleksandrov, “On the formulation of plane contact problems of the theory of elasticity during wear of interacting bodies [in Russian],” Doklady USSR Acad. of Sci., Is. 2, 827–831 (1983).

  5. D. V. Hrilitskii, Thermoelastic Contact Problems in Tribology [in Ukrainian], Kyiv, Inst. of Educ. Content Modernization, Kyiv (1996).

  6. A. G. Kuzmenko, Methods of Wear and Reliability Calculations [in Ukrainian], TUP, Khmelnytskii (2002).

  7. L. A. Galin, Contact Problems of the Theory of Elasticity and Viscoelasticity [in Russian], Nauka, Moscow (1980).

    Google Scholar 

  8. B. L. Pelekh, and A. V. Maksymuk, “Mathematical modeling of wear resistance processes of coated bodies,” Matematicheskoe Modelirovaniye Protsesov Iznosostoikosti Tel s Pokrytiyami [in Russian], Is. 37, 51–56 (1989).

    Google Scholar 

  9. B. L. Pelekh, A. V. Maksymuk, and I. M. Korovaichuk, Contact Problems for Layered Structural Elements and Bodies with Coatings [in Russian], Naukova Dumka, Kyiv (1988).

    Google Scholar 

  10. M. V. Chernets, Tribocontact Problems for Cylindrical Joints with Technological Non-Roundness [in Ukrainian], Politechnika Lubelska, Lublin (2013).

  11. Yu. G. Sheider, Operating Properties of Elements with Regular Microrelief [in Russian], ITMO Univer., St. Petersburg, (2001).

    Google Scholar 

  12. J. Brauer, and S. Andersson, “Simulation of wear in gears with flank interference – a mixed FE and analytical approach,” Wear, 254, Is. 11, 1216–1232 (2003); https://doi.org/https://doi.org/10.1016/S0043-1648(03)00338-7.

    Article  CAS  Google Scholar 

  13. W. Zhan, and P. Huang, “Numerical analysis of time-varying wear with elastic deformation in line contact,” Friction, 7, Is. 2, 143–152 (2019); https://doi.org/https://doi.org/10.1007/s40544-017-0195-1.

    Article  Google Scholar 

  14. A. E. Andreikiv, V. V. Panasyuk, and M. V. Chernets, “On the theory of wear of materials under dry friction,” Sov. Mater. Sci., 17, No. 2, 153–158 (1981); https://doi.org/https://doi.org/10.1007/BF00722904.

    Article  Google Scholar 

  15. A. E. Andreikiv, and M. V. Chernets, Assessment of Contact Interaction of Friction Machine Elements [in Russian], Naukova Dumka, Kyiv (1992).

    Google Scholar 

  16. A. A. Yevtushenko, and O. M. Ukhanskaya, “Thermomechanical wear criterion,” Treniye i Iznos [in Russian], 15, Is. 3, 379–388 (1994).

    Google Scholar 

  17. O. P. Kozachok, “Local friction wear of an elastic half space with protrusion,” Mater. Sci., 57, No. 6, 797–804 (2022); https://doi.org/https://doi.org/10.1007/s11003-022-00611-z.

    Article  Google Scholar 

  18. N. I. Muskhelishvili, Singular Integral Equations [in Russian], Nauka, Moscow (1968).

    Google Scholar 

  19. O. P. Kozachok, R. M. Martynyak, and B. S. Slobodian, Interaction of Bodies with Regular Relief in the Presence of an Intercontact Environment [in Ukrainian], Rastr-7, Lviv (2018).

  20. O. P. Kozachok, “Influence of partial filling of the gaps with compressible liquid on the contact of elastic bodies with wavy surfaces,” Mater. Sci., 56, No. 3, 310–318 (2020); https://doi.org/https://doi.org/10.1007/s11003-020-00431-z.

    Article  Google Scholar 

  21. O. P. Kozachok, “Contact of an elastic body with a rigid base containing grooves partially filled with nonwetting liquid,” Mater. Sci., 55, No. 5, 765–773 (2020); https://doi.org/https://doi.org/10.1007/s11003-020-00369-2.

    Article  Google Scholar 

  22. O. Kozachok, and R. Martynyak, “Contact problem for wavy surfaces in the presence of an incompressible liquid and a gas in interface gaps,” Math. and Mech. of Solids, 24, Is. 11, 3381–3393 (2019); https://doi.org/10.1177/1081286518781679.

Download references

Author information

Authors and Affiliations

  1. Pidstryhach Institute for Applied Problems of Mechanics and Mathematics, National Academy of Sciences of Ukraine, Lviv, Ukraine

    O. P. Kozachok

Authors
  1. O. P. Kozachok
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to O. P. Kozachok.

Additional information

Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 59, No. 1, pp. 121–127, January-February, 2023

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kozachok, O.P. Local Frictional Wear of an Elastic Half-Space with a Regular System of Protrusions. Mater Sci 59, 121–128 (2023). https://doi.org/10.1007/s11003-023-00752-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11003-023-00752-9

Keywords

Search

Navigation