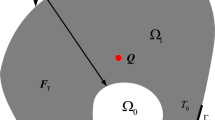
The problem of calculating the optimal annealing modes of functionally gradient bodies was formulated. An original method of its numerical solution based on the principle of stepwise parametric optimization is used. The finite element method was used to solve direct problems during the iterative construction of optimal heating-cooling for bodies of complex geometric shape and structure. The search for the optimal value of the control function does not require zero approximation and at each time step the function of one variable can be minimized.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. M. Kushnir, V. S. Popovych, and A. V. Yasinskyi, “Optimization and Identification in Thermomechanics of Heterogeneous Bodies,” Vol. 5 in: Ya. Yo. Burak (editor), Modeling and Ioptimization in Thermomechanics [in Ukrainian], Spolom, Lviv (2011).
M. H. Stashchuk, and E. M. Irza, “Thermal stressed states of the bodies of revolution made of functionally graded materials,” Mater. Sci., 55, No. 3, 311–319 (2019); https://doi.org/10.1007/s11003-019-00304-0.
M. H. Stashchuk, and Ye. M. Izra, “Thermal stresses in functionally graded bodies subjected to annealing,” Mater. Sci., 57, No. 4, 511–519 (2021); https://doi.org/10.1007/s11003-022-00572-3.
O. C. Zienkiewicz, and R. L. Taylor, Finite Element Method: Vol. 1. The Basis, Butterwoth Heinemann, London (2000).
M. H. Stashchuk, and Ye. M. Irza “Optimization of the modes of heat treatment of structural elements made of functionally graded materials,” Mater. Sci., 56, No. 1, 106–111 (2020); https://doi.org/10.1007/s11003-020-00403-3.
L. Ivas’kevich, G. Maksimovich, V. Kholodnyi, V. Belov, I. Tretyak, and T. Slipchenko, “Influence of gaseous hydrogen on the strength and plasticity of high-temperature strength nickel alloys,” Sov. Mater. Sci., 20, No. 3, 252–255 (1984); https://doi.org/10.1007/BF0072098.
F. Qin, O. Hembara, and O. Chepil, “Modeling of the influence of hydrogen on the bearing ability of elements of the powergenerating equipment under the conditions of temperature creep,” Mater. Sci., 53, No. 4, 532–540 (2018); https://doi.org/10.1007/s11003-018-0106-2.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 58, No. 4, pp. 20–25, July–August, 2022.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Stashchuk, M.G., Drobenko, B.D. & Izra, Y.M. Model of Calculation of Optimal Annealing Modes of Functionally Gradient Bodies. Mater Sci 58, 446–452 (2023). https://doi.org/10.1007/s11003-023-00683-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-023-00683-5