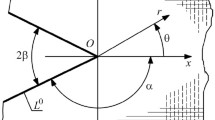
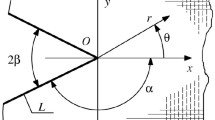
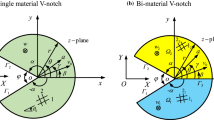
Using the singular integral equations method the antiplane elastic problem for elastic anisotropic body with sharp and rounded angular notches, is solved. The asymptotic dependence between the stress intensity factor and stress concentration in the sharp and rounded tips of arbitrarily oriented angular notch, is obtained. The unified approach to stress determination near sharp and rounded angular notches in orthotropic and anisotropic bodies under antiplane strain is developed on this basis.



Similar content being viewed by others
References
M. P. Savruk, and A. A. Kazberuk, “A unified approach to problems of stress concentration near V-shaped notches with sharp and rounded tip,” Int. Appl. Mech., 43, Is. 2, 182–197 (2007); https://doi.org/10.1007/s10778-007-0015-9.
M. P. Savruk, A. A. Kazberuk, and G. Tarasiuk, “Distribution of stresses over the contour of a rounded V-shaped notch under antiplane deformation,” Mater. Sci., 47, No. 6, 7–1 (2012); https://doi.org/10.1007/s11003-012-9449-2.
M. P. Savruk, and A. Kazberuk, “Concentration of Stresses in Solids with Notches,” Vol. 14 in V. V. Panasyuk (editor), Fracture Mechanics and Strength of Materials [in Ukrainian], Spolom, Lviv (2012).
M. P. Savruk, and A. Kazberuk, Stress Concentration at Notches, Cham: Springer Int. Publ. (2016);https://doi.org/10.1007/978-3-319-44555-7
M. P. Savruk, L. Y. Onyshko, and O. I. Kvasnyuk, “Distribution of stresses near angular notches on an orthotropic elastic plane under conditions of antiplane deformation,” Mater. Sci., 55, No. 3, 299–310 (2019); https://doi.org/10.1007/s11003-019-00303-1.
Chien-Ching Ma and Bao-Luh Hour, “Analysis of dissimilar anisotropic wedges subjected to antiplane shear deformation,” Int. J. Solids Struct., 25, Is. 11, 1295–1309 (1989); https://doi.org/10.1016/0020-7683(89)90093-0.
Chuan-I. Liu, and Ching-Hwei Chue, “Disappearance conditions of stress singularities for anisotropic bimaterial half-plane wedges under antiplane shear,” J. Appl. Mech., 74, 1–7 (2007); DOI:https://doi.org/10.1115/1.1989356.
Chuan-I. Liu, and Ching-Hwei Chue, “On the stress singularity of dissimilar anisotropic wedges and junctions in antiplane shear,” Compos. Struct., 73, Is. 4, 432–442 (2006); https://doi.org/10.1016/j.compstruct.2005.02.015
D. B. Bogy, “The plane solution for anisotropic elastic wedges under normal and shear loading,” J. Appl. Mech., 39, Is. 4, 1103–1109 (1972); https://doi.org/10.1115/1.3422837.
Ching-Hwei Chue, and C. Liu, “Stress singularities in a bimaterial anisotropic wedge with arbitrary fiber orientation,” Compos. Struct., 58, Is. 1, 49–56 (2002); https://doi.org/10.1016/S0263-8223(02)00041-7.
M. Xie, and R. A. Chaudhuri, “Three-dimensional asymptotic stress field at the front of a bimaterial wedge of symmetric geometry under antiplane shear loading,” Compos. Struct., 54, Is. 4, 509–514 (2001); https://doi.org/10.1016/S0263-8223(01)00123-4.
A. Blinowski, and J. Rogaczewski, “On the order of singularity at V-shaped notches in anisotropic bodies,” Arch. Mech., 52, Is. 6, 1001–1010 (2000).
Yu. Kukharchuk, G. Sulym, and S. Shevchuk, “Elastic equilibrium of two-dimensional bodies with angular points and thin inclusions,” Mashynoznavstvo, No. 1, 14–20 (1997).
G. Sulym, and N. Mackhorkin, “Asymptotic distribution of stress fields, displacements and potential energy of deformation in the vicinity of the corner point of a multi-wedge elastic body” [in Ukrainian], Acta Mech. Autom., 1, No. 2, 55–60 (2007).
N. Mackhorkin, and G. Sulym, “Distribution of deformation potential energy around the peak of an arbitrary wedge system under longitudinal shear,” Pryk. Probl. Mechaniki ta Matemat., No. 3, 62–69 (2005).
S. G. Lekhnitskii, Theory of Elasticity of Anisotropic Body [in Russian], Nauka, Moscow (1977).
T. C. T. Ting, Anisotropic Elasticity. Theory and Applications, Oxford University Press., Oxford (1996); https://doi.org/10.1002/zamm.19970770617.
G. Si, and G. Libovits, Mathematical Theory of Brittle Fracture [in Russian], G. Libovits (editor) Vol. 2, Mir, Moscow (1975).
L. A. Fil’shtinskii, “Longitudinal shear in anisotropic environment with notches,” Izvestiya Academii Nauk USSR, Ser.: Mechanika tverdogo tela, No. 4, 68–72 (1978).
L. A. Fil’shtinskii, “Elastic equilibrium of plane anisotropic environment weakened by arbitrary curvilinear cracks. Limit transition to an isotropic environment,” Izvestiya Academii Nauk USSR, Ser.: Mechanika tverdogo tela, No. 5, 7–16 (1976).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 58, No. 4, pp. 5–12, July–August, 2022.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Savruk, M.P., Onyshko, L.Y. & Kvasniuk, O.I. Stress Distribution Near Sharp and Rounded V-Notches In Anisotropic Elastic Body Under Antiplane Strain. Mater Sci 58, 427–436 (2023). https://doi.org/10.1007/s11003-023-00681-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-023-00681-7