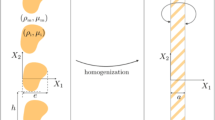
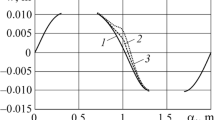
We consider a symmetric problem of harmonic wave loading of an infinite elastic matrix with a oneperiodic array of penny-shaped compliant inclusions. By using the periodic Green function, we reduce this problem to a boundary integral equation for a function characterizing a jump of displacements on one representative inclusion. The Green function used to describe the interaction of inclusions is adapted for the efficient determination of its representation in the form of exponentially convergent Fourier integrals. To solve the boundary integral equation, we use the method of collocations. The numerical results are obtained and analyzed for the mode I dynamic stress intensity factor in the vicinity of points of the contour of an inclusion depending on the wave number and the distance between the inclusions.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Ch. Zhang and D. Gross, On Wave Propagation in Elastic Solids with Cracks, Computational Mechanics Publications, Southampton (1998).
Y. Pennec, J. O. Vasseur, B. D. Rouhani, L. Dubrzynski, and P. A. Deymier, “Two-dimensional phononic crystals: examples and applications,” Surf. Sci. Rep., 65, No. 8, 229–291 (2010).
F.-L. Li, Y.-S. Wang, Ch. Zhang, and G.-L. Yu, “Boundary element method for band gap calculation of two-dimensional solid phononic crystals,” Eng. Anal. Bound. Elem., 37, No. 2, 225–235 (2013).
S. K. Kanaun and V. M. Levin, Self-Consistent Methods for Composites, Vol. 2: Wave Propagation in Heterogeneous Materials, Springer, Heidelberg (2008).
V. V. Mykhas’kiv, “Opening-function simulation of the three-dimensional nonstationary interaction of cracks in an elastic body,” Int. Appl. Mech., 37, No. 1, 75−84 (2001).
V. V. Mykhas’kiv, I. Ya. Zhbadynskyi, and Ch. Zhang, “On propagation of time-harmonic elastic waves through a double-periodic array of penny-shaped cracks,” Eur. J. Mech. A-Solid, 73, No. 1, 306−317 (2019).
G. S. Kit, Ya. I. Kunets, and V. V. Mikhas’kiv, “Interaction of a stationary wave with a thin penny-shaped inclusion of low stiffness in the elastic body,” Izv. Ros. Akad. Nauk, Mekh. Tverd. Tela, No. 5, 82–89 (2004).
V. I. Marukha, V. V. Panasyuk, and V. P. Sylovanyuk, Injection Technologies of Restoration of the Serviceability of Damaged Durable Structures [in Ukrainian], Spolom, Lviv (2009).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 56, No. 4, pp. 128–132, July–August, 2020.
Rights and permissions
About this article
Cite this article
Zhbadynskyi, I.Y., Butrak, І.О. Dynamic Stresses in the Elastic Matrix with One-Periodic Array of Compliant Penny-Shaped Inclusions. Mater Sci 56, 577–582 (2021). https://doi.org/10.1007/s11003-021-00466-w
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-021-00466-w