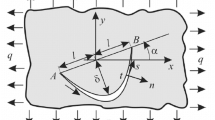
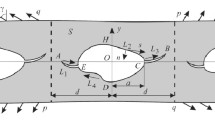
We construct a system of singular integral equations for the first fundamental problem of the plane elasticity theory for a quasiorthotropic body containing holes and cracks. For this purpose, we use the wellknown integral equations obtained for a system of curvilinear cracks (cuts) in a quasiorthotropic plane. The integral equations for a multiply connected region with holes are constructed with the help of the limit transition from open cuts in an infinite elastic plane to closed cuts. These singular integral equations of the first kind on closed contours (boundary of the body) are supplemented with the corresponding regularizing functionals guaranteeing the unique solvability of the integral equations for arbitrary right-hand sides.




Similar content being viewed by others
References
N. Hasebe and M. Sato, “Stress analysis of quasi-orthotropic elastic plane,” Int. J. Solids Struct., 50, 209–216 (2013).
M. P. Savruk and A. Kazberuk, “Plane eigenvalue problems of the theory of elasticity for orthotropic and quasiorthotropic wedges,” Fiz.-Khim. Mekh. Mater., 50, No. 6, 7–14 (2014); English translation : Mater. Sci., 50, No. 6, 771–781 (2015).
N. Hasebe and M. Sato, “Mixed boundary value problem for quasi-orthotropic elastic plane,” Acta Mech., 226, 527–545 (2015).
M.P. Savruk and A.B. Chornen’kyi, “Plane problem of the theory of elasticity for a quasiorthotropic body with cracks,” Fiz.-Khim. Mekh. Mater., 51, No. 3, 17–24 (2015); English translation : Mater. Sci., 51, No. 3, 311–321 (2015).
A. Kazberuk, M.P. Savruk, and A. B. Chornenkyi, “Stress distribution at sharp and rounded V-notches in quasi-orthotropic plane,” Int. J. Solids Struct., 85, 134 –143 (2016).
M. P. Savruk and A. Kazberuk, “Stress concentration near sharp and rounded V-notches in orthotropic and quasi-orthotropic bodies,” Theor. Appl. Fract. Mech., 84, 166–176 (2016).
F. E. Erdogan, M. Ratwani, and U. Yuceoglu, “On the effect of orthotropy in a cracked cylindrical shell,” Int. J. Fract., 10, No. 3, 369–374 (1974).
S. Krenk, “Influence of transverse shear on an axial crack in a cylindrical shell,” Int. J. Fract., 14, No. 2, 123–145 (1978).
I. S. Kostenko, “Elastic equilibrium of a closed orthotropic cylindrical shell with longitudinal notches,” Fiz.-Khim. Mekh. Mater., 16, No. 5, 67–70 (1980); English translation : Mater. Sci., 16, No. 5, 447–450 (1980).
V. P. Shevchenko, E. N. Donbnya, and V. A. Tsvang, “Orthotropic shells with cracks (cuts),” in: A. N. Guz’ (editor), Mechanics of Composites, Vols. 1–12, Concentration of Stresses, Vol. 7 [in Russian], Kiev, A.S.K. (1998), pp. 212–249.
Z. Suo, G. Bao, B. Fan, and T. C. Wang, “Orthotropy rescaling and implications for fracture in composites,” Int. J. Solids Struct., 28, No. 2, 235–248 (1991).
W. Zhang and X. Deng, “Asymptotic stress field in a degenerate orthotropic material containing a cohesive zone ahead of a crack tip,” J. Elast., 90, No. 3, 271–282 (2008).
S.-B. Cho and J.-K. Kim, “A study on stress singularities for V-notched cracks in anisotropic and/or pseudo-isotropic dissimilar materials,” Int. J. Korean Soc. Prec. Eng., 3, No. 2, 22–32 (2002).
J.-K. Kim and S.-B. Cho, “An analysis of eigenvalues and eigenvectors for V-notched cracks in pseudo-isotropic dissimilar materials,” Int. J. Korean Soc. Prec. Eng., 3, No. 2, 33–44 (2002).
M. P. Savruk, Two-Dimensional Problems of the Elasticity Theory for Bodies with Cracks [in Russian], Naukova Dumka, Kiev (1981).
S. G. Lekhnitskii, Anisotropic Plates [in Russian], Gostekhizdat, Moscow (1957).
I. A. Prusov and L. I. Lunskaya, “Elastic state of a piecewise homogeneous orthotropic plane with cuts,” Prikl. Mekh., 5, No. 8, 77–83 (1969).
N. I. Muskhelishvili, Some Basic Problems of the Mathematical Theory of Elasticity, Noordhoff, Groningen (1953).
M. P. Savruk and A. Kazberuk, Concentration of Stresses in Solids with Notches [in Ukrainian], in: V. V. Panasyuk (Ed.), Fracture Mechanics and Strength of Materials, Vol. 14, Spolom, Lviv (2012).
M. P. Savruk, P. N. Osiv, and I. V. Prokopchuk, Numerical Analysis in Plane Problems of the Theory of Cracks [in Russian], Naukova Dumka, Kiev (1989).
A. Kazberuk, M.P. Savruk, M. P., and A. B. Chornenkyi, “Stress concentration near elliptic holes or parabolic notches in quasiorthotropic planes,” Fiz.-Khim. Mekh. Mater., 52, No. 3, 7–14 (2016).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 52, No. 4, pp. 30–39, July–August 2016.
Rights and permissions
About this article
Cite this article
Savruk, M.P., Kazberuk, A. & Chornenkyi, A.B. Integral Equations of a Plane Problem of the Elasticity Theory for a Multiply Connected Quasiorthotropic Body. Mater Sci 52, 472–484 (2017). https://doi.org/10.1007/s11003-017-9979-8
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-017-9979-8