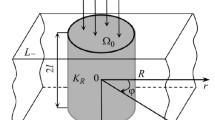
We consider a nonlinear boundary-value problem of heat conduction for an isotropic infinite heat-sensitive layered plate with heat-insulated faces containing a foreign through thermally active inclusion. By using the proposed transformation, we perform partial linearization of the initial heat-conduction equation. As a result of a piecewise-linear approximation of temperatures on the boundary surfaces of the foreign layers and the inclusion, the equation is completely linearized. We find an analytic-numerical solution of this equation with boundary conditions of the second kind in order to determine the introduced function with the use of the Fourier integral transformation. The computational formulas for the unknown values of temperature are presented in the case of a linear temperature dependence of the heat-conduction coefficients of structural materials for the two-layer plates. The numerical analysis is performed for a single-layer plate containing a through thermally active inclusion (the material of the plate is VK94-I ceramic and the material of the inclusion is silver).
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. F. Barvins’kyi and V. I. Havrysh, “Nonlinear problem of heat conduction for an inhomogeneous layer with internal heat sources,” Probl. Mashinostroen., 12, No. 1, 47–53 (2009).
V. I. Havrysh and D. V. Fedasyuk, “Method for the determination of temperature fields in a heat-sensitive piecewise-homogeneous strip with foreign inclusion,” Promyshl. Teplotekh., 32, No. 5, 18–25 (2010).
V. I. Gavrysh, “Modeling of temperature modes in heat-sensitive microelectronic devices with through foreign inclusions,” Élektron. Modelir., 34, No. 4, 99–107 (2012).
E. V. Golitsyna and Yu. R. Osipov, “Quasistationary three-dimensional problem of heat conduction in a rotating solid cylinder made of a composite material with nonlinear boundary conditions,” Konstruk. Kompoz. Mater., No. 4, 47–58 (2007).
Ya. S. Podstrigach, V. A. Lomakin, and Yu. M. Kolyano, Thermoelasticity of Bodies with Inhomogeneous Structure [in Russian], Nauka, Moscow (1984).
Yu. M. Kolyano, Methods of Heat Conduction and Thermoelasticity for Inhomogeneous Bodies [in Russian], Naukova Dumka, Kiev (1992).
G. A. Korn and T. M. Korn, Mathematical Handbook for Scientists and Engineers, McGraw-Hill, New York (1968).
V. A. Lomakin, Theory of Elasticity for Inhomogeneous Bodies [in Russian], Moscow University, Moscow (1976).
R. Berman, Thermal Conduction in Solids, Clarendon Press, Oxford (1976).
V. N. Yurenev and P. D. Lebedev, Thermotechnical Handbook [in Russian], Vol. 2, Énergiya, Moscow (1976).
V. Havrysh and O. Nytrebych, “Modeling of the thermal state in elements of microelectronic devices with through foreign inclusions,” Visn. Nats. Univ. “L’viv. Politekh.:” Komp’yut. Nauky Inform. Tekhnol., No. 719, 144–148 (2011).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 51, No. 3, pp. 32–38, May–June, 2015.
Rights and permissions
About this article
Cite this article
Havrysh, V.І. Nonlinear Boundary-Value Problem of Heat Conduction for a Layered Plate with Inclusion. Mater Sci 51, 331–339 (2015). https://doi.org/10.1007/s11003-015-9846-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-015-9846-4