Skip to main content
SpringerLink
Log in

Evaluation of the Potential Energy and Geometric Sizes of a Dislocation Crack

  • Published:
Materials Science Aims and scope

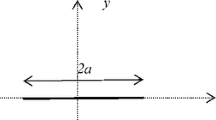
We study a dislocation crack in which a displacement jump is specified at one of its tips but the faces are closed at the other tip. The physical meaning of the problem is specified from the positions of fracture mechanics for a dislocation crack, which is associated with a mathematical model of a semiinfinite defect in solid body with an introduced extra plane of given thickness and a cut on its continuation. Within the framework of this model, we deduce an integral equation and find its solution, which enables us to establish the stress-strain state near the dislocation crack. As a result, we determine the geometric parameters and find the energy of a body weakened by the dislocation crack.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. V. I. Vladimirov, Physical Nature of the Fracture of Metals [in Russian], Metallurgiya, Moscow (1984).

    Google Scholar 

  2. A. N. Stroh, “A theory of the fracture of metals,” Adv. Phys., 6, 418–465 (1957).

    Article  Google Scholar 

  3. V. I. Vladimirov and Sh. Kh. Khannanov, “Interaction of dislocation pileups with dislocation cracks,” Fiz. Tverd. Tela, 11, No. 6, 1667–1676 (1969).

    Google Scholar 

  4. V. V. Panasyuk, A. E. Andreikiv, and V. S. Kharin, “Initiation and growth of microcracks generated by blocked dislocation pileups,” Fiz.-Khim. Mekh. Mater., 21, No. 2, 5–16 (1985).

    Google Scholar 

  5. J. Friedel, Dislocations, Pergamon Press, Oxford (1964).

    Google Scholar 

  6. J. P. Hirth and J. Lothe, Theory of Dislocations, McGraw-Hill, New York (1968).

    Google Scholar 

  7. N. G. Stashchuk, Problems of the Mechanics of Elastic Bodies with Cracklike Defects [in Russian], Naukova Dumka, Kiev (1993).

    Google Scholar 

  8. M. H. Stashchuk and M. I. Dorosh, “Determination of the geometric parameters and energy of the core of edge dislocation,” in: V. V. Panasyuk (editor), Fracture Mechanics of Materials and Strength of Structures [in Ukrainian], Karpenko Physicomechanical Institute, Ukrainian National Academy of Sciences, Lviv (2014), pp. 55–62.

    Google Scholar 

  9. S. P. Demidov, Theory of Elasticity [in Russian], Vysshaya Shkola, Moscow (1979).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Karpenko Physicomechanical Institute, Ukrainian National Academy of Sciences, Lviv, Ukraine

    M. H. Stashchuk & M. I. Dorosh

Authors
  1. M. H. Stashchuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. I. Dorosh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. H. Stashchuk.

Additional information

Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 51, No. 1, pp. 80–85, January–February, 2015.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Stashchuk, M.H., Dorosh, M.I. Evaluation of the Potential Energy and Geometric Sizes of a Dislocation Crack. Mater Sci 51, 88–95 (2015). https://doi.org/10.1007/s11003-015-9813-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11003-015-9813-0

Keywords

Search

Navigation