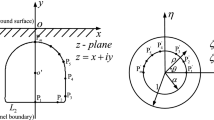
By the method of singular integral equations, we solve the axially symmetric problem of torsion for an elastic space containing a smooth cavity. We obtain the stress distributions and their maximum values at the edges of cavities of various shapes. We also compute the stress concentration factors on the surfaces of axially symmetric cavities in the entire range of values of the radii of rounding of their tips under the conditions of torsion of the elastic body. The numerical results are obtained for cavities of different configurations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M. P. Savruk and A. Kazberuk, “Common approach to the solution of the problems of stress concentration near sharp and rounded V-shaped notches,” Prikl. Mekh., 43, No. 2, 70–87 (2007).
M. P. Savruk, A. Kazberuk, and G. Tarasyuk, “Distribution of stresses over the contour of a rounded V-shaped notch under antiplane deformation,” Fiz.-Khim. Mekh. Mater., 47, No. 6, 7–14 (2011); English translation: Mater. Sci., 47, No. 6, 717–725 (2011).
M. P. Savruk, A. Kazberuk, and G. Tarasyuk, “Stress concentration near holes in the elastic plane under antiplane deformation,” Fiz.-Khim. Mekh. Mater., 48, No. 4, 5–13 (2012).
M. P. Savruk, Two-Dimensional Elasticity Problems for Bodies with Cracks [in Russian], Naukova Dumka, Kiev (1981).
H. Neuber, Kerbspannungslehre: Theorie der Spannungskonzentration Genaue Berechnung der Festigkeit, Springer, Berlin (1985).
N. Kh. Arutyunyan and B. L. Abramyan, Torsion of Elastic Bodies [in Russian], Fizmatlit, Moscow (1963).
V. S. Kravets’ and M. P. Savruk, “Stressed state of the space containing an axially symmetric crack on the surface of revolution,” in: 10th Internat. Symp. of Ukrainian Mechanical Engineers in Lviv [in Ukrainian], KINPATRI Ltd, Lviv (2011), pp. 102–104.
M. P. Savruk, “Integral equations for axisymmetric torsion in an elastic body containing cracks,” Fiz.-Khim. Mekh. Mater., 25, No. 6, 37–44 (1989); English translation: Mater. Sci., 25, No. 6, 584–592 (1989).
M. P. Savruk, S. D. Baidak, and V. O. Shabaikovych, “Torsion of an elastic space with crack on the surface of revolution,” Fiz.-Khim. Mekh. Mater., 29, No. 6, 87–93 (1993); English translation: Mater. Sci., 29, No. 6, 649–656 (1993).
N. I. Muskhelishvili, Some Basic Problems of the Mathematical Theory of Elasticity [in Russian], Nauka, Moscow (1966).
Yu. Murakami (editor), Stress Intensity Factors Handbook, Vol. 2, Pergamon, Oxford (1987).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 48, No. 6, pp. 102–109, November–December, 2012.
Rights and permissions
About this article
Cite this article
Kravets’, V.S., Vasyuta, R.V. Torsion of an elastic space containing an axially symmetric narrow cavity. Mater Sci 48, 807–817 (2013). https://doi.org/10.1007/s11003-013-9573-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-013-9573-7