Skip to main content
SpringerLink
Log in

Boundary-value problem of heat conduction for a piecewise homogeneous layer with foreign inclusion

  • Published:
Materials Science Aims and scope

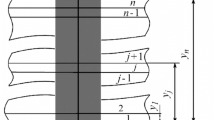
By using distributions, we deduce the heat-conduction equation with discontinuous and singular coefficients for an isotropic piecewise homogeneous layer containing a foreign cylindrical inclusion with heat release. With help of a piecewise linear approximation of temperature on the boundary surfaces of the inclusion and the Hankel integral transformation, we construct the numerical-analytic solution of the boundary-value problem of heat conduction with heat transfer. We also perform the numerical analysis for the case of a three-element layer containing an inclusion in the middle element.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. I. A. Motovilovets, Heat Conduction of Plates and Bodies of Revolution [in Russian], Naukova Dumka, Kiev (1969).

    Google Scholar 

  2. N. V. Belyaev and A. A. Ryadno, Methods of the Theory of Heat Conduction [in Russian], Part I, Vysshaya Shkola, Moscow (1982).

    Google Scholar 

  3. Ya. S Podstrigach, V. A. Lomakin, and Yu. M. Kolyano, Thermoelasticity of Bodies with Inhomogeneous Structures [in Russian], Nauka, Moscow (1984).

  4. Yu. M. Kolyano, Methods of Heat Conduction and Thermoelasticity for Inhomogeneous Bodies [in Russian], Naukova Dumka, Kiev (1992).

    Google Scholar 

  5. M. P. Savruk and V. M. Zelenyak, Two-Dimensional Problems of Thermoelasticity for Piecewise Homogeneous Bodies with Cracks [in Ukrainian], Rastr-7, Lviv (2009).

  6. Yu. M. Kolyano, Yu. M. Krichevets, E. G. Ivanik, and V. I. Gavrysh, “Temperature field in a multilayer half space containing a foreign cylindrical inclusion with heat release,” Promyshl. Teplotekhn., 16, No. 4 − 6, 30 − 34 (1994).

    CAS  Google Scholar 

  7. G. A. Korn and Th. M. Korn, Mathematical Handbook for Scientists and Engineers, McGraw-Hill, New York (1968).

    Google Scholar 

  8. V. I. Havrysh, D. V. Fedasyuk, and A. I. Kosach, “Boundary-value problem of heat conduction for a layer with foreign cylindrical inclusion,” Fiz.-Khim. Mekh. Mater., 46, No. 5, 115–120 (2010); English translation: Mater. Sci., 46, No. 5, 702–708 (2010).

Download references

Author information

Authors and Affiliations

  1. “L’vivs’ka Politekhnika” National University, Lviv, Ukraine

    V. I. Havrysh & A. I. Kosach

Authors
  1. V. I. Havrysh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. I. Kosach
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. I. Havrysh.

Additional information

Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol.47, No.6, pp.52–58, November–December, 2011.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Havrysh, V.I., Kosach, A.I. Boundary-value problem of heat conduction for a piecewise homogeneous layer with foreign inclusion. Mater Sci 47, 773–782 (2012). https://doi.org/10.1007/s11003-012-9455-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11003-012-9455-4

Keywords

Search

Navigation