Skip to main content
SpringerLink
Log in

Elastic ellipsoidal heat-conducting inclusion in a body under the action of a heat flux applied at infinity

  • Published:
Materials Science Aims and scope

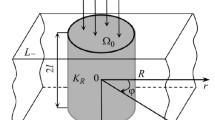
We find the exact analytic solution of the system of four singular integrodifferential equations obtained as a result of reduction of the three-dimensional thermoelastic problem for a body containing a heatconducting elastic ellipsoidal inclusion. It is assumed that the body is subjected to the action of a uniform heat flux applied at infinity in the direction perpendicular to the median plane of the inclusion. As a result, we deduce the relations for the stress concentration near the inclusion, the level of stresses inside the inclusion, and the corresponding stress intensity factors K II and K III. The influence of the configuration of the inclusion on the stress concentration and intensity is analyzed for some special cases of the problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Yu. N. Podil’chuk and V. V. Dobrivecher, “On the thermal stressed state of a transversely isotropic body containing a rigid elliptic inclusion,” Prikl. Mekh., No. 1, 11–17 (1996).

    Google Scholar 

  2. Yu. N. Podil’chuk and V. V. Dobrivecher, “On the thermal stressed state of a transversely isotropic body containing a rigid elliptic inclusion subjected to the action of a uniform heat flux in the plane of inclusion,” Prikl. Mekh., No. 8, 31–39 (1996).

    Google Scholar 

  3. A. H. Passos Morgado, Ya. Pivnik, and Yu. N. Podil’chuk, “Distribution of stresses in an infinite transversely isotropic body containing a rigid elliptic inclusion in a uniform heat flux,” Prikl. Mekh., No. 11, 3–10 (1995).

    Google Scholar 

  4. M. M. Stadnyk, “A method for the solution of three-dimensional thermoelasticity problems for bodies with thin inclusions,” Fiz.-Khim. Mekh. Mater., 30, No. 6, 30–40 (1994); English translation: Mater. Sci., 30, No. 6, 643–652 (1994).

    Article  Google Scholar 

  5. M. M. Stadnyk, “Elliptic crack in a space under the action of a heat flow at infinity,” Fiz.-Khim. Mekh. Mater., 46, No. 3, 38–41 (2010); English translation: Mater. Sci., 46, No. 3, 325–329 (2010).

    Article  Google Scholar 

  6. G. P. Cherepanov, Mechanics of Brittle Fracture [in Russian], Nauka, Moscow (1974).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Ukrainian National Forestry Engineering University, Lviv, Ukraine

    M. M. Stadnyk

Authors
  1. M. M. Stadnyk
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. M. Stadnyk.

Additional information

Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 47, No. 3, pp.16–23, May–June, 2011.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Stadnyk, M.M. Elastic ellipsoidal heat-conducting inclusion in a body under the action of a heat flux applied at infinity. Mater Sci 47, 284–293 (2011). https://doi.org/10.1007/s11003-011-9394-5

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11003-011-9394-5

Keywords

Search

Navigation