Mechanics and FEM estimation of gaps generated in star-ring active contacts of ORBIT motor during operation

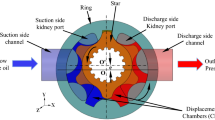
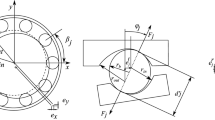
Abstract

We estimate deformations or gaps occurring at all the ideally form-closed contacts, that separate the chambers, in epitrochoid (cycloidal class) generated star-ring gears of ORBIT^® motors. The direct measurement of these deformations and gaps is not an easy task as the contact positions are inaccessible for installing any measuring device. Therefore, we target the accurate theoretical estimation of these deformations and gaps for any pressure or torque load. The problem poses statically indeterminate, as there are multiple contacts. We use FEM in Ansys^® environment to model the problem and its solution. We develop the model to its final stage with gradual improvement in assessing more accurate and realistic boundary conditions as well as loading patterns. We make an elaborate presentation of this process in this investigation report. Interestingly, in ORBIT motor momentary occurrence of gap at the transition active contact, i.e., the contact separating the two adjacent chambers with one in high pressure and the other in low pressure, is unavoidable. This occurs for a substantial period of a power cycle and sometimes in both transition contacts, that separate the overall high pressure zone and the low pressure zone. The inter-chamber leakages through these gaps are partially responsible for lowering the volumetric efficiency. The present investigation is limited to establishing a method of estimating deformation and gaps at the active contacts of such units. Our proposed method can be used for any such unit of any geometric design data and kinematic model.

Appendices

Appendix 1

1.1 Geometric generation of star-ring profiles

Referring to the Fig. 8, an unmodified epitrochoid is the locus of a point G, fixed outside of a circle (outer centrode) at $A_{ 0}$(= CG), which is rolling without slipping on another small circle (inner centrode) fixed inside the rolling circle. Now, let it is the first cycloidal motion. The envelope of the unmodified epitrochoid is generated by fixing the epitrochoid on its describing circle (inner centrode) and interchanging the tasks of two centrodes. Let this is the second cycloidal motion. These curves, generated by two cycloidal motions, will be closed (unicursal) curves if the diameters of these two centrodes are in the proportion of successive integers [let $Z/\left( {Z - 1} \right)$]. The epitrochoid will have (Z − 1) number of lobes. The envelope will have ${\text{Z}}$ number of crunodes (also called as double points) at a radius equal to $A_{ 0}$ with respect to the centre of the outer centrode. The modified epitrochoid, i.e., inwardly equidistance shifted epitrochoid, useful to design the star profile of GEROTOR, ORBIT and ORBITROL HST units, are generated using the first cycloidal motion and fixing rollers of radius $\left( {{\text{r}}_{m} } \right)$ equal to the amount of profile shift at an envelope crunode. The useful portion of the roller (i.e. circular arc) of radius ${\text{r}}_{m}$, is spread over twice the leaning angle, $\phi$. The first crunode is at $\psi = \pi /Z$ with respect to X′CY′ axis system. Other crunodes are at $2\pi /Z$ angle from each other. The circular arcs of useful spread of $2\phi$ angle or slightly more can be attached to all crunodes and then these arcs are joined with suitable identical arcs covering the envelope to make integral profile of the ring. Else in a ring plate with partial bush cavities at all crunodes, housing rollers of radius ${\text{r}}_{m}$ and length equal to the width of the ring b, is used (Fig. 1).

Fig. 8

Geometric generation of an useful modified epitrochoid (star) profile

The position vector of the modified epitrochoid generating point M, with respect to the centre of star O can be expressed as:

$$ \overrightarrow {\text{OM}} = \vec{C}_{ 0} + \vec{A}_{ 0} + \vec{r}_{m} $$

(12)

As already mentioned for unicursal epitrochoid and its envelope the following condition has to be satisfied.

$$ \frac{{R_{\text{0}} }}{{r_{ 0} }} = \frac{Z}{{\left( {Z - 1} \right)}}\;\;\;\text{i.e.,}\;\;\;\frac{{R_{ 0} }}{{\left( {R_{ 0} - r_{ 0} } \right)}} = Z $$

(13)

The coordinates of point M (X_m, Y_m) of the modified epitrochoid in dimensionless form, with respect to XOY co-ordinate system, are as follows:

$$ \begin{aligned} \bar{X}_{m} & = \bar{A}_{ 0} \cos \psi + \frac{1}{Z}\cos Z\psi \, - \bar{r}_{m} \cos \left( {\psi + \phi } \right) \\ \bar{Y}_{m} & = \bar{A}_{0} \sin \psi + \frac{1}{Z}\sin Z\psi \, - \bar{r}_{m} \sin \left( {\psi + \phi } \right) \\ \end{aligned} $$

(14)

The leaning angle ($\phi$) is an important parameter in the modification of epitrochoid profiles because in gearing action ($\pi / 2- \phi$) may be considered as the instantaneous pressure angle. In dimensionless parametric form it is expressed as:

$$ \phi \text{ = }\tan^{ - 1} \, \left( {\frac{{\sin \left( {Z - 1} \right)\psi }}{{A_{ 0} + \cos \left( {Z - 1} \right)\psi }}} \right) $$

(15)

where

$$ \psi = Z\xi $$

(16)

Figure 9 shows a typical epitrochoid generated star-ring (with roller) set.

Fig. 9

Modified epitrochoid generated star-ring

Appendix 2

2.1 Calculation of side thrust on the ring due to tightening it between the end plate and valve plate by fixing bolts (Fig. 1c) for Type-C FEM model

Each side flat area of the ring of this considered ORBIT motor unit is 3143.17 mm², as estimated by solid modelling.

Each bolt (M8 × 1.25) cross sectional (effective) area A_s, is 36.6 mm². Number of bolts 7.

We assume the Proof Strength ($\upsigma_{\text{y}}$) as 1098.34 MPa considering the steel’s strength class 12.9.

Co-efficient of friction ($f_{n}$) for metal to metal (steel) contact is 0.4.

Assuming that 70% of proof strength is applied on each bolt tightening force, axial force experienced by each bolt is $\left( { 0. 7\times\upsigma_{\text{y}} \times {\text{A}}_{\text{s}} } \right){\text{N}} = 0. 7\times 1 0 9 8. 3 4\times 3 6. 6\;{\text{N}} = 2 8 1 3 9. 4 7\;{\text{N}}$.

This force acts on each segmental area of the ring span between two bolts. This span is small and it may be assumed that pressure is uniform due to bolt tightening. Therefore, the pressure of ring plate is calculated as, $\frac{{\left( { 2 8 1 3 9. 4 7\times 7} \right)}}{ 3 1 4 3. 1 7} = 6 2. 6 6 8\;{\text{MPa}}$.

Now, we divide each span area into five radial parts of equal angle (360°/(7 × 5)  = 0.2857°). We multiply each small segment area by the calculated pressure and $f_{n}$ to get the tangential force on that segment (Fig. 4). The radial segmental areas in chronological order in a span, respective forces etc. are shown in Table 6. These forces are suitably applied in FEM numerical exercise.

Table 6 Calculation of concentric tangential forces on both the ring side flat area

Appendix 3

3.1 Conversion of FEM results from dimensional to non-dimensional form

Deformations and gaps in non-dimensional form ($\delta_{n}$) from the dimensional FEM results, for comparing with TEM (Maiti 1993) results and vice versa, are performed as follows. Data of the transition contacts at lobe 4 are considered for sample calculations (as shown in Tables 7 and 8).

Table 7 Lobe 4 contact deformations and gaps (in mm) ($\delta_{n}$) at 5, 11, 17.5 MPa

Table 8 Lobe 4 contact deformations and gaps (non-dimensional) ($\mathop {\bar{\delta }_{n} }\limits^{*}$) at 5, 11, 17.5 MPa

Now, deformations and gaps in non-dimensional form ($\mathop {\bar{\delta }_{n} }\limits^{*}$):

As per Eq. 10 in this manuscript,

$$ \mathop {\bar{\delta }_{n} }\limits^{*} = \delta_{n} /\left( {\Delta p_{i} \times f_{m} \times R_{ 0} } \right) $$

$$ {\text{where}}\;\; \, f_{m} = \left[ {\left( {\frac{{ 1- \upsilon_{t}^{ 2} }}{{E_{t} }}} \right) + \left( {\frac{{ 1- \upsilon_{e}^{ 2} }}{{E_{e} }}} \right)} \right] = 2\times \left( {\frac{{ 1- 0. 3^{ 2} }}{{ 2 0 7 0 0 0 { }}}} \right)\frac{{{\text{m}}^{ 2} }}{\text{N}} $$

Now, using Table 2 data of ORBIT motor,

For (i) 5 MPa ($\varDelta p_{i}$) we get the factor $\left( {\varDelta p_{i} \times f_{m} \times R_{ 0} } \right)$ = 0.00865.

For (i) 11 MPa ($\varDelta p_{i}$) we get the factor $\left( {\varDelta p_{i} \times f_{m} \times R_{ 0} } \right)$ = 0.019033.

For (i) 17.5 MPa ($\varDelta p_{i}$) we get the factor $\left( {\varDelta p_{i} \times f_{m} \times R_{ 0} } \right)$ = 0.03028.

As revealed from the converted data of FEM results into non-dimensional form for all three pressures (Table 8) they are very close to each other. When converted data from FEM results for all pressures for different shaft positions are plotted, it is visibly a single graph as shown in Fig. 10. Also the calculated data are very close to the earlier established TEM results.

Fig. 10

Plot of deformation or gap at lobe 4 active contact- in transition during $\xi = 0^\circ$ to $\xi_{ 0}$(= 4.2857°), but not in transition during $\xi = \;\xi_{o}$ to $2\xi_{ 0}$(=8.571°) FEM (Type C model) results (5, 11 and 17. 5 MPa), converted to non-dimensional form and TEM results