ZipLine: an optimized algorithm for the elastic bulk synchronous parallel model

Abstract

The bulk synchronous parallel (BSP) is a celebrated synchronization model for general-purpose parallel computing that has successfully been employed for distributed training of deep learning models. A shortcoming of the BSP is that it requires workers to wait for the straggler at every iteration. Therefore, employing BSP increases the waiting time of the faster workers of a cluster and results in an overall prolonged training time. To ameliorate this shortcoming of BSP, we propose ElasticBSP, a model that aims to relax its strict synchronization requirement with an elastic synchronization by allowing delayed synchronization to minimize the waiting time. ElasticBSP offers more flexibility and adaptability during the training phase, without sacrificing the accuracy of the trained model. ElasticBSP is realized by the algorithm named ZipLine, which consists of two phases. First, it estimates for each worker the end time points of its future iterations at run time, and then a one-pass algorithm over the estimated time points of all workers is employed to fast compute an optimal future time point for synchronization. We provide theoretical results about the correctness and performance of the ZipLine algorithm. Furthermore, we propose algorithmic and implementation optimizations of ZipLine, namely ZipLineOpt and ZipLineOptBS, which reduce the time complexity of ZipLine to linearithmic time. A thorough experimental evaluation demonstrates that our proposed ElasticBSP model, materialized by the proposed optimized ZipLine variants, converges faster and to a higher accuracy than the predominant BSP. The focus of the paper is on optimizing the synchronization scheduling over a parameter server architecture. It is orthogonal to other types of optimizations, such as the learning rate optimization.

1 Introduction

The parameter server framework (Dean et al., 2012; Ho et al., 2013; Langer et al., 2020) has been widely adopted to distributing the training of large deep neural networks (DNNs) (Chen et al., 2015; Zhang et al., 2017). The framework consists of multiple workers and a logical server that maintains globally shared parameters, typically represented as vectors and matrices (Li et al., 2014), and it supports two approaches: model parallelism and data parallelism (Chen & Lin, 2014).

Model parallelism (Dean et al., 2012; Langer et al., 2020) refers to partitioning of a large DNN model into small parts and distributing them to multiple workers for parallel training. Due to the complicated dependencies between layers of parameters in contemporary DNNs and predominant use of multiple GPUs (Coates et al., 2013; Cui et al., 2016), it is challenging to decouple the parameters of inter-layers or intra-layers for concurrent training of DNNs such as VGG (Simonyan & Zisserman, 2014) and ResNet (He et al., 2016). Additionally, since the inter-computer communication is determined by the connection bandwidth and the capacity of the switch in place, some partitions (in one computer) might need to wait long for the output of any dependent partitions (in another computer). While this is true for any single forward computing, typically in deep learning one iteration consists of both forward and back-propagation phases, and training large model requires a large number of iterations. Thus, model parallelism has rarely been seen in practice. To the contrary, data parallelism (Langer et al., 2020) has prevailed in industry (Dryden et al., 2016; Strom, 2015) and been implemented in many applications (Zhang et al., 2017; Li et al., 2015; Moritz et al., 2015). In this paper we focus on data parallelism.

Data parallelism refers to partitioning (sharding) of large training data into smaller equal-sized shards and assigning them to workers (see Fig. 1). Then, the entire DNN model is replicated to each worker. During training, each worker trains the replica model using its assigned data shard, sends the locally computed gradients to the server that maintains globally shared parameters (weights) and receives back updated global weights from the server. Weight synchronization is critical in this process as it provides to the server a way of controlling the iteration throughput, to boost the convergence speed against wall-clock time and the quality of convergence (i.e., the accuracy).

Fig. 1

Data parallelism under the parameter server (PS) framework running SGD. Each machine is labeled by a worker id. Workers fetch the weight w from PS and compute the gradients $\varDelta w$ based on loss function and the assigned data shard. PS receives gradients $\varDelta w$ from workers and update the weight w to a new weight $w'$ for the next iteration

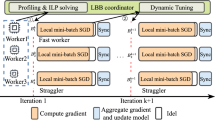
Due to its importance, a number of synchronization models have been proposed (Langer et al., 2020), the most important of which are the asynchronous parallel (ASP), the bulk synchronous parallel (BSP), and the stale synchronous parallel (SSP). ASP (Dean et al., 2012; Recht et al., 2011) is the simplest model, as it assumes no weight synchronization — workers always receive different versions of weights from the server at every iteration. BSP (Gerbessiotis & Valiant, 1994) is the most celebrated synchronization model but it has the straggler problem (Harlap et al., 2016) that might delay computation considerably. A critical component of it is the barrier synchronization, where workers reaching a barrier have to wait until all other workers have reached it as well (see Fig. 2). A straggler naturally exists in a heterogeneous environment where the processing speeds of workers vary. In a homogeneous environment, a straggler may also exist, which is caused by random node slowdown or communication delay. Communication delay roots in two sources, intra and inter-computer communications¹.

In the straggler problem, faster workers have to wait for the straggler. During the training phase of a DNN model, each worker, at each iteration, computes the model gradients based on the local data shard and the local weights (originally from the server) and sends the gradients to the server. The server aggregates the gradients from all workers, performs weight update (as one synchronization) and signals the workers to retrieve the latest weights for the next iteration. The workers replace their local weights with the latest weights from the server and start a new iteration.

SSP (Ho et al., 2013; Cui et al., 2014) provides an intermediate approach to the two extremes achieved by ASP and BSP. It performs synchronization, but mitigates the strict synchronization requirement of BSP. In principle, it monitors the difference in the number of iterations (iteration difference) between the fastest and the slowest workers and restricts it to be within a threshold by forcing the fastest worker to wait until the threshold is not exceeded.

Fig. 2

Vanilla BSP and our proposed ElasticBSP. Each barrier represents the time of weight synchronization among workers and a superstep represents the time period between consecutive barriers. In BSP the superstep is fixed to a number of k iterations and all workers have to wait for each other at the end of their k iterations ($k=1$ is shown, which is typical). In ElasticBSP, the time the barrier is imposed varies and each superstep can allow a different number of iterations per worker. These values are determined at run time by our proposed ZipLine method that achieves minimum overall waiting time of all workers (Color figure online)

The aforementioned models exhibit certain limitations. In ASP there is no need for synchronization, so the waiting time of the workers is eliminated. However, the convergence in the training might be dramatically affected due to inconsistent weight updates to the model. On the other hand, a prevalent shortcoming of the BSP is the strict synchronization requirement it imposes. As shown in Fig. 2, all workers are waiting for each other by a synchronization barrier. Each barrier represents the time point of the weight synchronization among workers and a superstep represents the time period between consecutive barriers. In BSP, a superstep is an iteration. There are also other BSP-like models, in which a superstep is set to k iterations, where k is fixed (Wang & Joshi, 2019). In SSP, while the strict synchronization requirement of BSP is removed, a user-specified threshold (fixed throughout the training period) is needed to control the maximum iteration difference among workers. Further, SSP offers a shortsighted solution to the problem, as it does not consider the computational capacity of each worker (i.e., how fast it is), merely relying on the number of iterations that each worker has completed.

To ameliorate these shortcomings, we propose ElasticBSP, a model that aims at relaxing the strict synchronization requirement of the predominant BSP to reduce worker waiting time and thus increase the iteration throughput, and at the same time limiting the staled gradients and their staleness values in the iterative stochastic gradient descent (SGD) convergent process. Compared to SSP, the proposed model considers the computational capacity of workers; it can therefore offer more flexibility and adaptability during the training phase, without sacrificing the accuracy of the trained DNN model. The key idea of ElasticBSP is that the server deals with online sequential decision making about the optimal future time to impose a synchronization barrier, whereas BSP and SSP solely rely on counting the number of completed iterations of workers to determine a synchronization. The decisions of ElasticBSP are the solutions to an online optimization with lookahead problem (Dunke, 2014). As such, the time a synchronization barrier is imposed varies and each superstep can permit a different number of iterations per worker, offering elasticity (see Fig. 2). ElasticBSP is realized by an efficient method, named ZipLine that fast solves the optimization problem. It materializes the ElasticBSP model. ZipLine consists of two phases. First, R future iteration intervals of each worker are predicted at run time based on their most recent intervals, assuming a stable environment (the lookahead). Then, a one-pass algorithm operates over the predicted intervals of all workers and determines the next optimal synchronization time (i.e., a time that minimizes the overall workers’ waiting time). Our experiments show that the algorithm can effectively balance the trade-off between the accuracy and the convergence speed to accommodate different environments or applications. Notably, ElasticBSP, materialized by the proposed optimized version of ZipLine, converges faster and achieves higher accuracy than BSP, SSP and ASP for large-sized DNNs using moderately small learning rates.

An earlier version of this work introduced the ElasticBSP scheme and a general version of the ZipLine algorithm (Zhao et al., 2019b). In this extended version, we present optimized versions of the ZipLine algorithm, a comprehensive analysis of the methods including mathematical proofs on the correctness, as well as extensive experiments. It is important to note that ElasticBSP focuses on optimization of the synchronization scheduling over the parameter server framework for distributed training and can be applied to other distributed machine learning methods based on SGD optimization. As such, it is orthogonal to other DNN optimization techniques, such as the learning rate optimization (Liu et al., 2019). The major contributions of this work are as follows:

• We propose ElasticBSP, a novel synchronization model for scaling the training of distributed deep learning models. ElasticBSP replaces the strict synchronization requirement of other BSP-like models with an online sequential decision making about the best time to impose the next synchronization barrier. The model guarantees convergence when the number of iterations of the training phase is large.

• We provide theoretical results about the correctness and performance of the ZipLine, a one-pass algorithm that can efficiently materialize the ElasticBSP model. ZipLine performs online optimization with lookahead to decide the next best synchronization time. It outperforms sensible baselines that exhibit polynomial time complexity.

• We propose two optimizations of ZipLine: ZipLineOpt and ZipLineOptBS. The former is an algorithmic optimization that relies on a pruning technique to reduce the search space of the solution. The latter is an implementation optimization that employs an advanced data structure offering fast search operations and manages to achieve linearithmic time complexity.

• We present a thorough experimental evaluation of our ElasticBSP model materialized by ZipLine on four deep learning models (varying in size and structure) on three popular image classification datasets (varying in class size, sample size and image resolution). The results show that ElasticBSP converges much faster than BSP and to a higher accuracy than BSP and other state-of-the-art alternatives when the learning rate is not large. In particular, ElasticBSP demonstrates a superior performance on the large-sized DNNs with respect to convergence speed and accuracy using small step sizes.

The remainder of the paper is organized as follows. Section 2 provides a brief background of the state-of-the-art synchronization models and their limitations under the parameter server framework. Section 3 introduces our proposed ElasticBSP synchronization model and its properties. Section 4 formally defines the problem of interest and provides problem analysis. In Sect. 5, we first present algorithmic details of sensible baselines; then we present our proposed method ZipLine, and its two optimized variants ZipLineOpt and ZipLineOptBS that can realize ElasticBSP. Section 6 presents a thorough experimental evaluation of the methods. We review the related work in Sect. 7 and conclude in Sect. 8.

2 Background

In this section, we first present a synchronization cost model of training a deep learning model, assuming the parameter server framework; in particular, cost related to the wall-clock idle time of processors. Then, we briefly present the three most closely related state-of-the-art synchronization models employed by the server for achieving parallel Stochastic Gradient Descent (SGD) computation through synchronous (or asynchronous) data communication between the server and workers, and discuss their main advantages and limitations.

2.1 Synchronization cost model

In the parameter server framework, the server becomes aware of a worker’s iteration intervals through the contiguous timestamps of the worker’s push requests. Formally, given a worker $p \in [1,n]$, a single iteration interval $T_{iter}^p$ consists of computing time $T_{comp}^p$ and communication time $T_{comm}^p$ (see examples in Figs. 2 and 3). In addition, we know that the communication time can be broken down into data transmission time $T_{trans}^p$ and waiting time $T_{wait}^p$ until the synchronization occurs. During data transmission, a worker sends gradients to the server and the server sends weights back to the worker. We ignore lower level communication since the size of the exchanged data at low level (e.g., TCP/IP) is significantly smaller than that of gradients and weights. The time cost of a single iteration of a worker p is:

$$\begin{aligned} \displaystyle \gamma _{iter}^p = \displaystyle \gamma _{comp}^p + \gamma _{trans}^p + \gamma _{wait}^p \end{aligned}$$

(1)

where $\gamma _{iter}^p$, $\gamma _{comp}^p$, $\gamma _{trans}^p$ and $\gamma _{wait}^p$ represent the associated length of a period $T_{iter}^p$, $T_{comp}^p$, $T_{trans}^p$ and $T_{wait}^p$ respectively.

Note that $\gamma _{comp}^p$ is a constant since the hardware computational capacity is fixed and the batch size does not change — each iteration computes a single batch. Also, $\gamma _{trans}^p$ is a constant since workers are training the same model and both the weights and the gradients are of the same data size. On the other hand, $\gamma _{wait}^p$ is a variable that can be controlled by the parameter server.

Recall that each worker has to wait for the signal from the server to pull the weights after a synchronization (aggregation) operation in BSP. Let us denote as $t_p$ the time point that the worker p started waiting and $t_{sync}$ the time point that the synchronization completes (i.e., imposed barrier ends). Then $T_{wait}^p = [t_p, t_{sync}]$ and its length $\gamma _{wait}^p = t_{sync} - t_p$. Therefore, from the optimization perspective, for n workers in a distributed system, the cost of applying one synchronization barrier b at time $t_{sync}$ is dominated by the longest waiting time of any of the n workers, say $\tau _{wait}^b= \max (\gamma _{wait}^p), p \in [1, n]$ for a superstep $\tau$ ending with a barrier b. Assuming that there is a set B of synchronization barriers defined by |B| synchronization timestamps during the training period, the synchronization cost function of n workers is defined as:

$$\begin{aligned} c_{sync}=c(n, B) = \sum _{b=1}^{|B|}\tau _{wait}^b \end{aligned}$$

(2)

We aim to find the optimal set B:

$$\begin{aligned} B^* = \mathop {{{\,\mathrm{argmin}\,}}}\limits _B c_{sync} \end{aligned}$$

(3)

We propose the ZipLine method to minimize every $\tau _{wait}^b$ in the training phase.

Fig. 3

Iteration intervals measured by timestamps of contiguous push requests from workers. A dotted line represents the time a push request arrives at the server from a worker. An iteration interval consists of gradient computing period (solid block) and communication period (blank block). All workers’ ending timestamps can be mapped onto a timeline. Each timestamp on the timeline is associated to one of the workers. A set which is represented by the bracket always keep n unique values (colors) of workers. ZipLine scans the points from left to right on the timeline, takes one color point into the set per iteration (Color figure online)

2.2 Synchronization models for parallel SGD

DNNs learn to estimate a model using an optimizer based on a training dataset via an iterative convergent algorithm. The most effective optimizer for training DNNs is the stochastic gradient descent (SGD). SGD iteratively updates the model weight w in sequential fashion (Zinkevich et al., 2010): $\textstyle w^t = \textstyle w^{t-1} - \eta \cdot (g^{t-1} + \partial \varPhi (w^{t-1}))$, where t represents the $t_{th}$ iteration, g is the gradient(s) of the loss function with respect to the weights w and $\varPhi$ is the regularizer. Parallel SGD (Zinkevich et al., 2010) refers to SGD running in a distributed environment. Assuming a distributed environment and the data parallelism approach of a parameter server framework are used as we demonstrated in Fig. 1, the entire DNN model is replicated to n workers, while the server maintains globally shared weight parameters. During the training, each worker trains the replica model using its assigned data shard, sends the computed gradients to the server (via a push operation) and retrieves updated weights from it (via a pull operation). The following represent state-of-the-art synchronization models for training DNNs.

Bulk Synchronous Parallel (BSP)  In BSP, the server updates the weight w in two steps. First, it aggregates the gradients $\displaystyle g_p, p\in [1,n]$ from n workers in iteration $\displaystyle t-1$ such that $\displaystyle g^{t-1} = \displaystyle \frac{1}{n}\sum_{p=1}^{n} g_p^{t-1}$. Second, it updates the weight $w^{t-1}$ for next iteration t,

$$\begin{aligned} \displaystyle w^t = \displaystyle w^{t-1} - \eta \cdot (g^{t-1} + \partial \varPhi (w^{t-1})) \end{aligned}$$

(4)

After the weight update, it signals n workers that the weight $w^t$ is available to pull. The synchronization of workers is mandatory per iteration, but costs extra time on waiting for the stragglers; that is because of the first aggregation step in which the server does not reduce the gradient $g^{t-1}$ until it receives gradient $g_p^{t-1}$ from all n workers. After the second step, all the workers receive the same (synchronized) weights. In this way, the server is controlling the gradient updates and makes parallel SGD logically function as serial SGD on a single computer. The synchronization in BSP guarantees the data consistency of w as shown in Fig. 2. This strategy works very well when all the workers have similar speed.

Asynchronous Parallel (ASP) ASP (Dean et al., 2012; Recht et al., 2011) is an alternative approach on updating the weight w. It is based on the idea of the workers working independently and the server updating the weights immediately as soon as any gradient becomes available. In this fashion, weight synchronization is not required and the waiting time of workers is eliminated. With no synchronization, the weight updates on the server become asynchronous gradient updates. See the examples in Figs. 3 and 8a. It appears as if ASP is better than BSP since it removes the control costs and waiting time overhead. Besides, the number of weight updates of ASP becomes n times more than that of BSP for n workers (by Eqs. 4, 5), which means ASP enjoys larger iteration throughput. However, the weight updates become chaotic:

$$\begin{aligned} w^t = w^{t-1} - \eta \cdot (g_p^{s-1} + \partial \varPhi (w^{t-1})), p \in [1,n], s \le t \end{aligned}$$

(5)

Here t represents the iteration of the fastest worker(s) whereas s is the iteration of the slower worker(s). The gradients computed at iteration $s = t - c$ by the slower worker(s) then become stale for c iterations, where c denotes the iteration difference; c also represents the staleness value of the staled gradients of the slower worker(s). If c is large, the staled gradients add noise to the iterative weight updates (see an intuitive example in Fig. 8a) and when there are many c-staled gradients present, it renders to a convergence uncertainty (Zhou et al., 2018). We further elaborate it in Sect. 4.2 as we also consider limiting the staled gradients in designing our algorithm.

Stale Synchronous Parallel (SSP) SSP (Cui et al., 2014; Zhao et al., 2019a) provides an intermediate solution to BSP and ASP; it addresses the straggler problem of BSP and mitigates the gradient staleness problem of ASP. It achieves that by allowing workers to run independently but ensuring that the fastest worker(s) do not run $\beta$ iterations further than the slowest worker(s). In other words, SSP uses a threshold $\beta$ to constrain the iteration difference c among workers at any moment during the training so that $c \le \beta$. Note that $\beta$ has to be fixed to a small number, otherwise SSP might behave as ASP. Since c is bounded by a small $\beta$, the harm that the staled gradients bring to the convergence is reduced. In (Ho et al., 2013; Zhao et al., 2019a) authors provide theoretical analysis to prove that SSP guarantees convergence for a large number of iterations with a small $\beta$.

The SSP scheme works as follows: it counts the number of iterations each worker has completed. When the fastest worker is running its tth iteration and the slowest worker is running its ($s = t - \beta - 1$)th iteration, the fastest worker has to wait for the slowest worker to reach its ($t - \beta$)th iteration. In this way, SSP achieves a synchronization between the fastest and slowest workers by setting barriers that put a stop to the fastest workers. After the synchronization, the fastest and the slowest workers compute the gradients based on the same weight w. Since $\beta$ is small, the model will converge for a large number of iterations (Ho et al., 2013).

3 ElasticBSP model

Motivated by the limitations of the current state-of-the-art synchronization models in the parameter server setting, we propose Elastic Bulk Synchronous Parallel (ElasticBSP), a novel synchronization model, to ameliorate drawbacks of current models without sacrificing their benefits. ElasticBSP offers elasticity in the sense that the distance between two consequent synchronization barriers is not fixed (as in BSP), but is determined online (at runtime). Also, the waiting time is not determined by a fixed iteration difference between the fastest and the slowest workers (as in SSP), but based on an optimal synchronization strategy that minimizes the overall worker waiting time. There are two key properties of ElasticBSP:

• The server deals with online sequential decision making regarding the optimal time that the next synchronization barrier should be imposed (a time point when the minimum waiting time for the entire system is achieved). Each decision is the solution of an online optimization problem that utilizes information about the most recent time interval of each worker available to the server to predict their R future intervals (the lookahead). The need for looking into only R future intervals comes from the need to control the decision algorithm’s run time, since the run time can increase exponentially as R increases. A bound in R also ensures that ElasticBSP does not behave as the ASP model, but provides a convergence guarantee and maintains an accuracy similar to that of SSP.

• The theoretical analysis about the convergence of ElasticBSP follows the theoretical analysis of DSSP (Zhao et al., 2019a). In DSSP, an upper bound $s'$ exists as a fixed staleness threshold in the entire training phase and guarantees the convergence when the iteration number is large and $s'$ is small. In an analogous manner, in ElasticBSP a small iteration difference $\beta$ exists that is defined within the R future intervals. The parameter $\beta$ serves as the upper bound $s'$ defined in some period $\tau$ (a superstep) and the convergence is guaranteed when the iteration number is large (similarly to the case of DSSP). A new $s'$ is defined for every next period $\tau$. By the end of each period $\tau$, the synchronization barrier b is posed to all the workers where gradient aggregation is carried out on the server, similarly to BSP — the model weights are then synchronized and will be available to all workers in the next iteration.

Consider the illustrative example of Fig. 4², where n=10 workers need to synchronize. The server first predicts the R=15 future iteration intervals for each worker (dots in distinct color) based on their latest two contiguous push timestamps. Intervals between dots of the same color represent iteration intervals of a worker. Then, a decision needs to be made about the optimal time to impose a synchronization barrier that minimizes the overall waiting time for the 10 workers in wall-clock time. The squared dots (in red) in the example represent the intervals of each worker that inform the optimal synchronization time (minimum waiting time), determined by the distance between the leftmost and rightmost red square dots. In particular, the rightmost red square dot is where a barrier b shall be imposed. In Fig. 4, worker 9, represented by the leftmost red dot, will be the first to arrive in the barrier b and wait for the synchronization to occur. Note that for each worker, the respective red square dot might represent a push timestamp that occurs at a different iteration than that of other workers. In ElasticBSP, the server maintains this information and learns the best time to signal the workers to perform a pull operation and synchronize the weight parameters. In Fig. 4, pull will be broadcasted by the server shortly after the rightmost red square dot, which represents the time that the slowest worker (i.e., worker 4) uploaded the gradients to the server, and therefore aggregation of gradients is possible.

Fig. 4

Predicting the time to synchronize. The sky blue triangles in the first column are the starting points of the predicted future iterations at which we have learned the most recent iteration intervals of all workers. Each dot represents the ending time of an iteration. Workers (labelled from 0 to 9) have unique color. Starting from them, we predict next R=15 future iteration intervals of the 10 workers. The objective is to find the dots of distinct colors that are closest to each other (i.e., dots vertically aligned near any time-spot). Three strategies are shown for comparison: ZipLine ($min\_d$ in red squares), a random barrier pick ($rnd\_d$ in grey blue diamonds) and vanilla BSP ($bsp\_d$ in sky blue triangles). $min\_d$, $rnd\_d$ and $bsp\_d$ represent the overall workers’ waiting time cost in milliseconds in wall-clock time. ZipLine has the minimum cost (599ms) (Color figure online)

4 The problem

In this section, we formally define the problem of interest. Part of the originality of our work can be attributed to the fact that we formalize the problem as an online optimization with lookahead problem. Online optimization with lookahead is an optimization paradigm that utilizes a limited preview of future input data (lookahead) to inform sequential decision making under incomplete information. For distributed deep learning, this optimization paradigm provides a better description of a parameter server’s informational state than other well-established synchronization models that assume nothing is known about the future. Specifically, the solution to the optimization problem will provide a prediction of the optimal time $t^*_{sync}$ to impose the next synchronization barrier b. Our approach to tackling the straggler problem via synchronous paradigms is fundamentally different from current approaches that either strictly control the time to impose a synchronization barrier (i.e, BSP) or determine it based on ad hoc runtime decisions (i.e, SSP).

Recall that during the execution, the parameter server receives push requests coming from n workers. Once a request is received, the server keeps a record of the worker p and associates it with a timestamp representing the time of the request. Modern data centers and distributed services provide high-availability (HA) solutions ($99.999\%$ available time) (Benz & Bohnert, 2013). It is therefore realistic to assume a running environment with a stable network and machines, where the duration of subsequent iterations of a worker (including batch processing, gradient computing and data communication) are relatively stable in the foreseeable future.

This assumption allows to heuristically estimate the R future iteration intervals of each worker within some duration (see Figs. 3 and 4) based on their most recent iteration interval history. Thus, R can not be too large due to the bound of the duration. For instance, if a worker p arrives at time t and presents an iteration interval $\gamma _{iter}^p$, then the future R iterations can be estimated to occur at time $t+\gamma _{iter}^p, t+2 \cdot \gamma _{iter}^p,\ldots ,t+R \cdot \gamma _{iter}^p$. After a completion of a synchronization, we then estimate the R future iteration intervals for each worker based on their most recent historical data, the problem is then to determine the best time spot within the R future iterations to impose the new synchronization barrier – a time spot that will minimize the waiting time for all workers (see Fig. 5).

Fig. 5

The flow of prediction and synchronization of ElasticBSP with three workers consists of two phases: (i) the monitoring phase, and (ii) the prediction phase. The purpose of the monitoring phase is to allow the server to learn the iteration interval of all the workers. It requires at least two push requests per worker. The prediction phase consists of predicting the R future iterations of each worker and using ZipLine to get the optimal time to impose the next synchronization barrier. Once a synchronization occurs, the two phases repeat again. This example illustrates that even of one of the workers (round orange) has different speeds between synchronizations, ElasticBSP can still find the optimal next synchronization time, since it always uses the most recent history of workers. The solid objects (square, circle and diamond) are occurred iteration interval timestamps of three workers, the hidden objects are their estimated future timestamps of iterations. The lower figure shows what happens after the completion of a synchronization at the barrier in the upper figure under the same wall clock time line. Note that the “circle" worker suddenly changed to shorter iteration interval during the monitoring phase at the lower figure (Color figure online)

Note that this assumption is not limiting our approach. In practice, if a worker does not behave in a predictable way, say due to a failure, it will be taken out of the distributed computation (and will be ignored by our method). Similarly, if a minor fluctuation in the duration of an interval occurs, for example due to a network glitch of any of the workers, our method might be affected by an erroneous prediction which might cause a sub-optimal imposition of a synchronization barrier. Nonetheless, that error will not be carried forward to the next decision. That is because we always use the most up-to-date history of worker time intervals to find the time to impose the next synchronization barrier which also accommodates the occasional network bandwidth shifts and peak hours users activity. As such, the effect to the overall approach will be negligible (if any).

4.1 Problem definition

Consider the parameter server framework and let n be the number of workers. For each worker $p \in [1, n]$, the server predicts R future iteration intervals and stores a set $S^p = \{e_1^p, e_2^p,..., e_R^p\}$, where $e_i^p, i \in [1, R]$ represents the ending timestamp of the i-th iteration of worker p.³ We only need to store ending timestamps (and no starting timestamps), as they are the only ones required for determining a synchronization time. From each of the n sets $S^p, p \in [1, n]$, we pick one element $e_j^p, j \in [1, R]$ to construct a new set $Z = \{e_j^p \}, p\in [1,n]$ of $|Z|=n$ ending timestamps (one for each worker). The smallest timestamp in Z ($\min (Z)$) corresponds to the fastest worker and the largest timestamp in Z ($\max (Z)$) corresponds to the slowest worker, respectively. Then, the difference $d_Z = \max (Z) - \min (Z)$ represents the waiting time of the fastest worker if Z is used to impose a synchronization barrier. Note that $t_{sync}=\max (Z)$ represents the time point to impose the synchronization barrier b and $d_Z=\tau _{wait}^b$ represents the waiting time overhead if barrier b is imposed. As it becomes clear, any set Z can determine the time $t_{sync}$ and represents one candidate solution to the optimization problem. From the space of all candidate solutions, we are looking for the optimal one $Z^*$ (as shown in Fig. 6) that exhibits the minimum $d_{Z^*}$ and determines the optimal $t^*_{sync}$ at which we will impose the next synchronization barrier b. The following formalizes the problem.

Fig. 6

ZipLine scans the points (push timestamps) on the timeline as in Fig. 9 and evaluates all 141 possible sets Z (each of which consists of distinct workers) of the example from Fig. 4 in ascending order. For each set Z, the overall worker waiting time $d_Z$ is obtained and plotted on y-axis. ZipLine finds the optimal set $Z^*$ that minimizes $d_{Z^*}$ (i.e., 599 milliseconds) which lies at the 97th combination (highlighted in red) (Color figure online)

Problem 1

Given n workers, each represented by a set $S^p = \{e_1^p, e_2^p,..., e_R^p\}$, where $e_i^p$ is the ending time of the i-th future iteration of worker $p, p \in [1, n]$ and $R \in {\mathbb {N}}$, find a solution Z containing one element from each $S^p$, such that $d_Z$ is minimized.

Hence, our objective function is:

$$\begin{aligned} Z^* = \mathop {{{\,\mathrm{argmin}\,}}}_Z d_Z \end{aligned}$$

Knowing $Z^*$, we can determine the optimal time $t^*_{sync}=max(Z^*)$ to impose the next synchronization barrier b. At the end of the distributed training of a model, a set B of synchronization barriers will have been imposed and the overall waiting time overhead can be derived by Eq. (2).

4.2 Choosing $Z^*$ for ElasticBSP

It is possible that more than one $Z^*$ exists among all possible Z’s derived from the n sets $S^p$ (see example in Fig. 7). In this case, the $Z^*$ with the earliest (smallest) timestamp is preferred for ElasticBSP. Figure 8 illustrates the reason by depicting two cases.

Fig. 7

A plot of the cost $d_{Z}$ of candidate solutions Z evaluated by ZipLine. As ZipLine iteratively scans the elements of $\varOmega$ from the leftmost to the rightmost element on the timeline, we compute $d_{Z}$ the cost of each candidate solution Z (the smaller the cost $d_Z$ the better the solution Z). The run is based on the SmallR dataset of Table 2, for n=1,000 and R=15. There are 15,000 elements in $\varOmega$. ZipLine evaluates a total of 13,795 candidate solutions, FullGridScan 15,000 candidate solutions and GridScan only 15 candidate solutions. We only plot the $d_{Z}$ values that have a cost of less than 1600 milliseconds; we highlight the optimal $d_{Z^*}$ and a few sub-optimal $d_{Z}$s. Red triangles indicate $d_{Z^*}$ (Color figure online)

Fig. 8

a shows how staled gradients $\delta$ bring noise to the weight updates. The noise may drift the weight convergence away from the optimal direction (i.e., to poor local minima of the loss function). b Suppose we have two optimal solutions $Z^*_A$ and $Z^*_B$. Each column lists the number of iterations each worker has completed in each solution. Both solutions $Z^*_A$ and $Z^*_B$ have equal $d_Z$. The solution with the smaller iteration difference $d^{iter}$ (i.e., 4) introduces fewer staled gradients to the model weights and therefore is preferred (Color figure online)

Figure 8a illustrates how SGD is working asynchronously under the parameter server setting. For instance, two workers are shown with different processing speeds on a mini-batch (one iteration), where worker $p_2$ runs faster than worker $p_3$. If synchronization between $p_2$ and $p_3$ happens at every iteration following BSP, then no delayed gradients updates are introduced. On the contrary, in the case of asynchronous gradient updates, noise might be injected (i.e., staled gradients with large staleness value (Ho et al., 2013)) to SGD and lead to divergence, especially when the noise is accumulated over a large number of iterations. Intuitively, synchronizing as early as possible reduces the staled gradients and decreases their staleness. Theorem 1 and Corollary 1 formalize this intuition. In a nutshell, in the case of asynchronous gradient updates, the longer it takes for a synchronization barrier to be imposed, the more stale the gradients will be, potentially rendering the weight convergence uncertain.

In Fig. 8b, there are 5 workers and two equivalent optimal solutions are considered ($Z^*_A$ and $Z^*_B$). In each solution, a different number of iterations have been completed by each worker since last synchronization. In $Z^*_A$, the iteration difference $d^{iter}$ between the faster and slower workers is 10, whereas in $Z^*_B$ the difference is 4. According to Fig. 8(b), $Z^*_B$ will have fewer staled gradient updates than $Z^*_A$, because its iteration difference $d^{iter}$ (i.e., 4) is smaller than that of $Z^*_A$ (i.e., 10). We show that if the workers have different processing speeds (on an iteration), then the iteration difference $d^{iter}$ among them increases as asynchronous gradient updates last longer (i.e., the synchronization barrier is imposed at the later time). Therefore, if multiple $Z^*$s with the same $d_{Z^*}$ exist, we prefer to impose a synchronization barrier represented by the earliest time $t^*_{sync}$.

Theorem 1

(The earlier the synchronization barrier is imposed, the less stale the gradients) Consider two workers $p_i$ and $p_j$, $i,j \in [1, m]$, $m\in {\mathbb {N}}$ and $i \ne j$, and their iteration intervals $t_{p_i}$ and $t_{p_j}$, respectively, where $t_{p_i} < t_{p_j}$ (i.e., $p_i$ is faster than $p_j$). Let the difference of the number of iterations they complete within a time period t be given by $d^{iter} = \frac{t}{t_{p_i}} - \frac{t}{t_{p_j}}$. Then, within a time period $t' > t$, we have $d^{iter'} > d^{iter}$, where $d^{iter'}$ is the iteration difference within $t'$.

Proof

Suppose we have two workers $p_i,p_j, i,j\in [0, m], i \ne j$ and their iteration intervals being $t_{p_i}=\lambda t_{p_j}, \lambda \in (0,1)$ (i.e., $p_i$ being faster than $p_j$). Within a time period t, their iteration difference is given by $d^{iter} = \frac{t}{t_{p_i}} - \frac{t}{t_{p_j}} = \frac{t(t_{p_j}-t_{p_i})}{t_{p_i}t_{p_j}} = \frac{t(1 - \lambda )}{t_{p_i}}$ ①. Within a longer time period $t'=t+k, k>0$, their iteration difference is given by $d^{iter'} = \frac{(t+k)(1 - \lambda )}{t_{p_i}}$ ②. Therefore, for a longer run time $t' > t$, the iteration difference is given by ② − ① $= \frac{k(1- \lambda )}{t_{p_i}} > 0$ since $\lambda \in (0,1)$. $\square$

Intuitively, if a synchronization period (a superstep) lasts longer, then a larger iteration difference among workers is introduced by asynchronous gradients updates.

Corollary 1

Since less staled gradients have less negative impact to the rate of convergence (Ho et al., 2013), early synchronization is preferred in asynchronous parallel training phase for better convergence with respect to the rate and the accuracy.

5 Methodology

To address Problem 1, we first investigate a brute-force approach, naive search. Since naive search cannot scale to a large number of workers, we develop an optimized version of it named FullGridScan as a baseline. Then, we introduce our proposed method ZipLine and its optimized variants ZipLineOpt and ZipLineOptBS and compare them with the baselines. Table 1 summarizes the computation and space complexity of the different approaches.

Table 1 Summary of computation and space complexities of methods

5.1 Exhaustive search methods

Naive search In order to find the minimum difference $d_{Z^*}$, a straightforward approach is to use a brute-force search method. The method determines the optimal solution $Z^*$ by first constructing all candidate solutions Z. Each Z contains one element from each set $S^p = \{e_1^p, e_2^p,..., e_R^p\}, p \in [1,n], R \in {\mathbb {N}}$. Since there are n sets $S^p$ (one for each worker), and each set $S^p$ has R elements, there are $R^n$ candidate solutions in total. Then, for each candidate solution Z, it computes its $d_Z$ value. The solution $Z^*$ for which the minimum value $d_{Z^*}$ is yielded, is the optimal solution. The computation complexity of naive search is ${\mathcal {O}}(R^n)$. The space complexity is ${\mathcal {O}}(R^n)$ to store the $R^n$ possible solutions.

GridScan Since naive search is not practical, we present an optimized heuristic brute-force method, GridScan (Algorithm 1) as a baseline. GridScan will eventually serve as the basic component of FullGridScan. Let the future R iteration timestamps of n workers form a $n \times R$ matrix ${\mathcal {M}}$, where each row of the matrix ${\mathcal {M}}_p$ represents a worker $p, p\in [1,n]$ and each row element ${\mathcal {M}}_{p,i}=e^p_i, i\in [1,R]$ represents each of the R predicted iteration interval points (timestamps). Now, observe that for any designated element in ${\mathcal {M}}$, we can search for elements belonging to the remaining rows that have timestamps close to the timestamp of the designated element (as shown in line 10). Then, the elements found in the remaining rows along with the original designated element form a candidate solution Z, for which we can obtain $d_Z$.

Accordingly, we can consider a designated row, and we can iteratively consider all its R elements and define R candidate solutions Z, each one associated to each of the designated elements of the designated row. Following this procedure, the optimal solution $Z^*$ will be the one that exhibits the minimum $d_{Z^*}$. To guarantee we do not miss any early element (on the timeline), we set the designated row to be that with the minimum (earliest) timestamp (i.e., ${\mathcal {M}}_{p,1}$) (see line 4). Finding the designated row costs $\varTheta (n)$. The total computation complexity is ${\mathcal {O}}(R^2n)$. The outer loop iterates over the R elements of the designated row and the inner loop iterates over the R elements of each of the remaining $n-1$ rows to construct candidate solutions. During the search, we only need to maintain the currently best solution $Z^*$ (i.e., n elements) and the associated $d_{Z^*}$. Therefore, it requires space complexity $\varTheta (n)$. Along with the storage of the Rn elements of the matrix ${\mathcal {M}}$, the space complexity is ${\mathcal {O}}(Rn)$.

FullGridScan In GridScan, R candidate solutions Z are constructed, each associated with a $d_Z$. Due to its design, it is possible that GridScan will miss some solutions with a smaller $d_{Z}$. In order to discover potentially better solutions during the search, we also implement FullGridScan as a better baseline than GridScan. FullGridScan iterates over all n rows (i.e., workers) of the matrix ${\mathcal {M}}$, each time defining a designated row ${\mathcal {M}}_p, p\in [1,n]$ and applying GridScan using Algorithm 1, but skipping line 4. Therefore, FullGridScan considers Rn candidate solutions compared to the R candidate solutions considered by GridScan. As FullGridScan needs to apply GridScan n times, its computation complexity is ${\mathcal {O}}(R^2n^2)$. The space complexity of FullGridScan remains the same as GridScan.

5.2 Search by ZipLine

We are now in position to describe ZipLine, our proposed method to solve the optimization problem. Given n workers each represented by set $S^p = \{e_1^p, e_2^p,..., e_R^p\}$ where $p \in [1,n]$, R is the number of future iterations being considered, and $e_i^p$ is a triple $\langle t, p, i\rangle$ in which t is the ending timestamp of the ith future iteration of worker p (that is, p and i are the meta data identifying each time point $e_i^p$), ZipLine (Algorithm 2) determines the optimal solution $Z^*$ in two steps:

Step 1 (Initialization). We first merge the elements of all sets $S^p = \{e_1^p, e_2^p,..., e_R^p\}$, $p \in [1,n], R \in {\mathbb {N}}$ into a set $\varOmega$ such that $\varOmega = \cup _{p=1}^{n}S^p$. Note that since $e_i^p$ is a triple $\langle t, p, i\rangle$, there are no duplicate elements in merging all sets $S^p$ into $\varOmega$. We then sort the elements in $\varOmega$ in the ascending order of their timestamp t. Thus, the elements in $\varOmega$ are ordered by time, where the leftmost element represents the earliest event. In case of multiple elements having the same timestamp value, the order of these elements can be arbitrary, which does not affect the final solution. To enable the optimization strategy in ZipLineOptBS (described in Sect. 5.3.2), here we sort the elements having the same timestamp value in ascending order by their worker id.

We then initialize Z with n elements of $\varOmega$, by iteratively taking the leftmost element of $\varOmega$ and putting it into Z, while making sure that the n elements in Z have unique p values (that is, the n elements in Z come from n workers) (line 5–9). This is achieved by continuously adding the leftmost element of $\varOmega$ to Z, one at a time, and replacing the element of Z having the same p value as the newly added element from $\varOmega$ until we have n elements in Z. This process is the same as if we pick one element of each $S^p$ starting from the leftmost of each $S^p$ and these picked elements are most adjacent to each other with respect to their timestamps. Then, we compute $d_Z$ of the candidate solution Z (i.e., the difference between minimum and maximum timestamps of Z, representing a worker’s waiting time). Initially, $Z^* = Z$ and $d_{Z^*}= d_{Z}$.

Step 2 (Iterative procedure). Starting from the leftmost element the method iteratively scans all elements of $\varOmega$ one at a time, until $\varOmega$ is empty (line 13-23). At each iteration, the method constructs a candidate solution Z. Recall that a candidate solution Z must contain one element from each set $S^p = \{e_1^p, e_2^p,..., e_R^p\}, p \in [1,n], R \in {\mathbb {N}}$ (see Fig. 9). As new elements are evaluated, the method only needs to check the worker id p of each element $e_i^p$ in the current solution Z. This is to prevent adding an element to the solution that comes from the same set $S^p$ (i.e., same worker p). Whenever a new element is added to a solution Z, the previous element of Z that has the same p value with the newly added element from $\varOmega$ is removed/replaced. For each solution Z, the associated $d_Z$ is computed by searching for the element of Z that has the smallest timestamp and taking the difference between the timestamp of the new element and the smallest timestamp. If $d_Z$ is smaller than the current $d_{Z^*}$, then we set $Z^* = Z$ and $d_{Z^*}= d_{Z}$.

Fig. 9

ZipLine scans all elements on the timeline, from left to right, one element at a time. When a solution Z of n distinct elements is formed, $d_Z$ is computed. At the end of the process the optimal solution $Z^*$ is found that yields the minimum $d^*_Z$. If multiple solutions exhibit the same $d^*_Z$s, then the solution Z that occurred first (chronologically) is selected by Corollary 1. In this example, $d_6$ and $d_{10}$ have the same minimum value — $Z_6$ associated with $d_6$ is chosen as the optimal solution (Color figure online)

At the end of the process, after Rn iterations (the size of $\varOmega$), the optimal solution $Z^*$ that exhibits the smallest $d_{Z^*}$ is found. At each iteration, the removal or replacement operation of an element costs ${\mathcal {O}}(n)$. Also, since the elements in Z may not be sorted after the replacement operations, it takes ${\mathcal {O}}(n)$ to find the element in Z with the earliest timestamp to compute $d_Z$. Therefore, the total computation complexity of ZipLine is ${\mathcal {O}}(Rn^2)$. The algorithm only uses $\varTheta (n)$ space to store $Z^*$ and ${\mathcal {O}}(Rn)$ for the storage of all elements in $\varOmega$, therefore the space complexity is ${\mathcal {O}}(Rn)$.

5.2.1 ZipLine optimality

We claim that our greedy algorithm, ZipLine, leads to an optimal solution and we provide a formal proof of the claim.

Theorem 2

(ZipLine optimality) ZipLine leads to an optimal solution $Z^*$.

Proof

(Sketch) The proof is based on propositions of two lemmata. Lemma 1 claims that ZipLine always finds an acceptable solution. Lemma 2 claims that there is not a better one. $\square$

Lemma 1

ZipLine always finds an acceptable solution. An acceptable solution Z includes one element from each set $S^p = \{e_1^p, e_2^p,..., e_R^p\}, p \in [1,n], R \in {\mathbb {N}}$.

Proof

In Algorithm 2, a candidate solution Z is first initialized in the while loop in Lines 5–9 to contain n elements of $\varOmega$ where n is the number of workers, and Line 7 ensures that there are no two elements in Z having the same p value (i.e., coming from the same worker). That is, the initialized Z contains n timestamps, one from each worker. Thus, it is an acceptable solution. Other candidate solutions are formed in Lines 14-19, which also ensures that Z contains n elements and no two elements have the same p value. Thus, all candidates are acceptable solutions. Therefore, ZipLine finds an acceptable solution. $\square$

Lemma 2

ZipLine produces a solution $Z^*$ that is no worse than other solutions X. In other words, for any acceptable solution $X \ne Z^*$, it holds that $d_{X} \ge d_{Z^*}$.

Proof

Assume that $X=\langle x_1, x_2, \dots , x_n\rangle$ is an acceptable solution, where n is the number of workers , $x_i\in \varOmega$, different $x_i$’s have different p values (i.e., they come from different workers), and $x_1< x_2< ... < x_n$ (ordered according to the timestamp). There are two possible cases:

• 1. There exists $o \in \varOmega$, such that $o \notin X$ and $x_j< o < x_k$ (where $x<y$ means that x comes before y in $\varOmega$), where $j,k \in [1,n]$ and $j < k$. There are three situations in this case:

  • o’s worker id (i.e., its p value) is identical to that of $x_1$. In this situation, Lines 7-8 and Lines 17-18 in Algorithm 2 would replace $x_1$ with o, resulting in a better candidate solution Z with $d_Z\le (x_n-x_2)\le (x_n-x_1) = d_X$ (where $x_n-x_2$ or $x_n-x_1$ is the difference in timestamps between $x_n$ and $x_2$ or $x_n$ and $x_1$). That is, Z is a better or equally-good solution compared to X.

  • o’s worker id (i.e., its p value) is identical to that of $x_n$. ZipLine would form a candidate solution Z before reaching $x_n$ since $x_1, \dots , o, \dots , x_{n-1}$ form a candidate solution (that is, it contains n timestamps, one from each worker), controlled by the while loops (Lines 5-9 and Lines 15-19). Since $d_Z=(x_{n-1}-x_1)\le (x_n-x_1)=d_X$, Z is a better or equally-good solution compared to X.

  • o’s worker id is identical to that of an element $x \in X$, where $x_1< x < x_n$ (i.e., $x \in \{x_2,...,x_{n-1}\}$). Assuming that o is from the same worker as $x_j$ where $1<j<n$, ZipLine would choose between o and $x_j$ the one with the later timestamp to form a candidate Z due to the while loops in Lines 5–9 and Lines 15–19. In this case, $d_Z=x_n-x_1=d_X$. That is, Z is as good as X.

• 2. There does not exist a triple $o\in \varOmega$ such that $o \notin X$ and $x_j< o < x_k$ (where $x<y$ means that x comes before y in $\varOmega$), where $j,k \in [1,n]$ and $j < k$ (that is, $x_i$’s are next to each other in the sorted $\varOmega$). In this case, X would be a candidate generated by ZipLine (Lines 5–9 and Lines 15–19 in Algorithm 2 ensure this).

Since ZipLine returns the candidate $Z^*$ with the lowest $d_{Z^*}$ among all the candidates it generates, ZipLine returns a solution no worse than X. $\square$

Lemmas 1 and 2 prove our claim stated in Theorem 2 that ZipLine leads to an optimal solution $Z^*$.

5.3 ZipLine optimizations

As ZipLine scans through new elements of $\varOmega$, a new candidate solution $Z'$ is formulated every time by replacing an element of the previous candidate solution Z with the new element. Recall that a candidate solution Z must contain one element from each set $S^p = \{e_1^p, e_2^p,..., e_R^p\}, p \in [1,n], R \in {\mathbb {N}}$. Satisfying this condition and searching for $min(Z')$ in $Z'$ to compute $d_{Z'}$ dominate the cost of ZipLine. Since the elements in $Z'$ may not be ordered according to their timestamps due to the replacement operations in previous iterations, the search for $min(Z')$ costs ${\mathcal {O}}(n)$. Thus, the cost of ZipLine becomes ${\mathcal {O}}(Rn^2)$ for scanning through the Rn elements in $\varOmega$.

Below, we discuss two optimizations that manage to effectively reduce the ZipLine cost to ${\mathcal {O}}(n\log {}n)$, by reducing the cost of the replacement operation and the search of $min(Z')$ in $Z'$ to ${\mathcal {O}}(\log {}n)$. The first optimization takes advantage of the fact that elements are sorted in the time axis, from the earliest to the latest to prune the search space of finding the $min(Z')$. The second is an implementation optimization that utilizes a more efficient data structure to boost the search process.

5.3.1 Search space pruning optimization (ZipLineOpt)

In this version of ZipLine, we utilize an array data structure to store and keep the elements of a candidate solution $Z'$ in the temporal order of their arrival at the array. When a new element of $\varOmega$ is evaluated by ZipLine, we know that the oldest element in the array has the minimum timestamp and the most recently added element has the maximum timestamp. To determine the $min(Z')$ there are two cases: (i) with probability $\alpha , \alpha \in (0,1)$, the oldest element in the array has the same color as the newly added element, and therefore we simply remove the oldest element and set the new minimum timestamp to be the one succeeding it in the array. After adding the new element, we can compute $d_{Z'}$ directly due to random access to the array data structure. Thus, the cost of searching for $min(Z')$ is reduced to ${\mathcal {O}}(1)$ with probability $\alpha$; (ii) with probability $1-\alpha , \alpha \in (0,1)$, the oldest element in the array does not have the same color as the newly added element, and therefore there is no need to re-compute the $d_{Z'}$, since it is larger than $d_{Z}$ by Theorem 3.

Theorem 3

Suppose $e_i \in Z$ and $e_1< e_2< ... < e_n$ where $i \in [1,n]$ and $|Z|=n$ and let $d_Z = e_n - e_1$. Now, assume we add a new element $e'$, where $e' \ge e_n$ to formulate a new solution $Z'$. To satisfy that $|Z'|=n$, we need to remove the element $e_j$ from Z that has the same color as $e'$. If $j > 1$, then $d_{Z'} \ge d_Z$, where $d_{Z'} = e' - e_1$.

Proof

Let $d' = e' - e_n$. We know $d' \ge 0$ as $e' \ge e_n$. By definition, $d_{Z'} = e' - e_1 = d' + e_n - e_1 = d' + d_Z \ge d_Z$. $\square$

In either case, we still have to remove the element of the same color from the array data structure before adding the new element; otherwise, ZipLine collapses and better candidates may be missed. To do so, for case (i) we just need to add the new element to the end of the array and treat the current second element of Z as the first one. For case (ii), we need to traverse the array Z until the element with the same color as the new element is found, which is then removed by shifting the elements after the found element by one spot. This search and delete operation costs ${\mathcal {O}}(n)$ and occurs with probability $1-\alpha$. At last, we add the new element to Z and move on to the next element in $\varOmega$. We call this variant of ZipLine as ZipLineOpt. The main difference between ZipLine and ZipLineOpt is that in ZipLineOpt Z is kept sorted so that there is not need to search Z for min(Z) (i.e., the smallest timestamp value in Z) to compute $d_{Z}$ and we can take advantage of the case (i) with probability $\alpha$.

Since $\varOmega$ has Rn elements, the computation cost of ZipLineOpt becomes $\alpha \cdot {\mathcal {O}}(Rn) + (1-\alpha )\cdot {\mathcal {O}}(Rn^2)$. Table 4 shows that empirically it is the fastest when $n \le 100$.

5.3.2 Implementation optimization (ZipLineOptBS)

To further optimize ZipLineOpt, we focus on the case of $1-\alpha$ which requires ${\mathcal {O}}(n)$ traversal of the array Z to remove the element of the same color as the newly added element. The optimization is achieved by making use of the auxiliary data structure ${\mathcal {M}}$ that is used to hold all the $S_i^P$’s for $p=[1:n]$ and $i=[1:R]$ before forming $\varOmega$. Specially, ${\mathcal {M}}$ is a $n\times R$ matrix that stores the R future timestamps of n workers, each row holding the R timestamps of a worker. ${\mathcal {M}}$ was used to construct $\varOmega$ and was not used after $\varOmega$ was constructed by the ZipLine or ZipLineOpt algorithm. In this optimized version of the algorithm (denoted as ZipLineOptBS), we use ${\mathcal {M}}$ to help locate the element in Z that has the same color with the new element from $\varOmega$.

For every element of $\varOmega$, its color (or worker id), its iteration index i (the ith future iteration of a worker p) and the timestamp associated to that index i are stored as an element of the matrix ${\mathcal {M}}$. Thus, for any new element $e_i^p$ of $\varOmega$ to be added to Z, we can retrieve that worker’s previous element $e_{i-1}^p$ from ${\mathcal {M}}$ in ${\mathcal {O}}(1)$ based on its worker id $p \in [1,n]$ and iteration index $i \in [1, R]$. Once we get the timestamp of the worker’s previous iteration $e_{i-1}^p$, we can locate it in the array Z by the timestamp value using a binary search (BS) algorithm, since the elements of Z are sorted (in an ascending order). The BS reduces the search cost to ${\mathcal {O}}(\log {}n)$. Thus, the cost of the $1-\alpha$ case is reduced to $(1-\alpha )\cdot {\mathcal {O}}(Rn\log {}n)$. The use of the auxiliary data structure ${\mathcal {M}}$ with binary search (BS) allows ZipLineOptBS to bring the cost of ZipLine down to $\alpha \cdot {\mathcal {O}}(Rn) + (1-\alpha )\cdot {\mathcal {O}}(Rn\log {}n)$, where $\alpha \in (0,1)$.

In a rare case in which a few contiguous elements of different colors (i.e., different workers) in Z have the same timestamp value, the algorithm can still find the target element by locating the first and the last elements with the same timestamp in the array Z in ${\mathcal {O}}(\log {}n)$ and then traversing only between the two to find the one with the same color (worker id) as the target element by following the worker id order. Due to the fact that the elements with the same timestamp value are ordered by their worker id, this search operation costs ${\mathcal {O}}(\log {}k), k \le n$ using the binary search.

6 Experimental evaluation

In this section, we run experiments that aim to evaluate:

• A. The runtime performance of the ZipLine algorithm and its variants compared to two sensible baselines, FullGridScan and GridScan. We also evaluate the scalability performance of ZipLine as a function of the number of workers n and the parameter R.

• B. The performance of the ElasticBSP model compared to the BSP, ASP and state-of-art synchronization models, such as SSP. We are interested in finding which one converges faster and/or to a higher accuracy, and also which one is able to complete a fixed number of epochs faster.

6.1 ZipLine performance

Dataset To evaluate the performance of algorithms, we generate synthetic data-sets based on various realistic scenarios of the number of workers n and values of the parameter R. For each worker we randomly define its iteration interval to be in the range of 1000ms to 1500ms. Note that the iteration interval depends on the computational complexity of the DNN model, the mini-batch size and the GPU model. Therefore, whether the time unit is millisecond or second does not affect the computing time of the algorithm as long as the total number of time points generated is same.

We built a generator⁴ which takes the number of workers n and the iteration interval range as arguments to simulate iteration interval time points of the n workers. The generator simulates the iterations of all the workers for a short period and outputs the time points of the iterations of all the workers close to the same time window. Our algorithms then take the generated data of the recent time window such as the last two iteration time points (gradient push requests timestamps in practice) to predict the next R future iterations for all the workers and start to search the optimal synchronization time window which yields the least waiting time of all the workers. The iteration interval $i_p$ assigned to each worker p is randomly sampled from an uniform distribution in range 1000 to 1500 milliseconds as we specified earlier. The initial time $s_p$ of each worker is obtained by adding a base starting time to a randomly generated small number sampled from an uniform distribution in range 10 to 50 milliseconds. We add this small number to simulate latency between independent parallel processes initializing on the different computers in a cluster. To estimate the jth iteration time point in the future for worker p, we calculate $j \cdot i_p + s_p$. Table 2 lists the different configurations of the datasets for n and R.

Table 2 Synthetic datasets with varying number of n and R

SmallR ($R=15$) is used to evaluate the performance of algorithms as a function of the number of workers n. LargeR ($R=150$) is used to evaluate the scalability of the algorithms as a function of R.

Environment All experiments about ZipLine’s runtime performance were run on a server with 24x Intel(R) Xeon(R) CPU E5-2620 v3 @ 2.40GHz and 64GB ram. The running environment was Ubuntu 16.04. The algorithms and the datasets generator were developed in C++11.

6.1.1 Zipline ability to find the optimal solution

We have provided theoretical results about the optimality of Zipline in Sect. 5.2.1. Here, we provide empirical evidence of Zipline’s ability to find the optimal solution and compare it to the ones found by the competitive algorithms. We experiment with the datasets of Table 2. For each run scenario, we compute the $d_{Z^*}$ of the solution $Z^*$ that each algorithm is able to find (Table 3), along with the associated computation time cost (Table 4). The results reported are an average of 10 runs. The results suggest that the family of the ZipLine methods always finds the optimal solution $Z^*$ – same as the one found by the exhaustive method, FullGridScan. But, it is able to do so one or two orders of time faster (depending on the ZipLine variant considered). This is because the search space of candidate solutions evaluated by FullGridScan is much larger than that of ZipLine. On the other hand, the GridScan heuristic, while is comparable to ZipLine in terms of speed, consistently fails to find the optimal solution. Among the variants of ZipLine, ZipLineOptBS adds some overhead compared to ZipLineOpt for fewer workers, but as the number of workers increases, it is able to compensate the cost.

Table 3 Search accuracy comparison on $d_{Z^*}$ — the least waiting time in milliseconds/ms found by algorithms

6.1.2 ZipLine scalability

The number of candidate solutions Z formed by elements of the Matrix ${\mathcal {M}}$:$n \times R$ increases exponentially to the number of workers n and polynomially to the value of the parameter R (i.e., $R^n$), as described in Sect. 5.1. We have showed in Table 4 that as the number of workers n increases, the computation time of FullGridScan increases much faster than that of the ZipLine family of algorithms. We have also discussed that for a fixed number of workers, as R increases the computation time of FullGridScan increases much faster.

Table 4 Average computation time of algorithms in microseconds/$\mu s$ for finding an optimal solution for one synchronization

To further elaborate on the behavior of the ZipLine variants, in Fig. 10 we provide an illustration of their run time comparison (we do not plot FullGridScan to improve the comparative analysis of the ZipLine variants). It can be observed that when n is small (e.g., below 100), ZipLineOpt is faster than ZipLineOptBS. But, as n increases (e.g., above 200), ZipLineOptBS outperforms ZipLineOpt. That is because ZipLineOptBS has to maintain two auxiliary data structures and accessing the second one (the table ${\mathcal {M}}$) introduces extra cost, compared to ZipLineOpt. However, this extra cost is amortized into many scan iterations when the number of elements of $\varOmega$ is large (i.e., Rn) (i.e., most iterations are very fast and only few of them are expensive). Observe in Fig. 10 that for R=150, ZipLineOptBS grows significantly slower than ZipLineOpt. Same trend is depicted for R=15 as well – as n increases, ZipLineOptBS outperforms ZipLineOpt. Therefore, we recommend to employ ZipLineOpt when n is small (e.g., $n \le$ 100) and employ ZipLineOptBS otherwise. Most research and industrial labs can typically afford a GPU cluster with 4 to 8 nodes (workers), in which scenario ZipLineOpt is preferred. The GridScan heuristic can serve as an alternative when one is willing to sacrifice accuracy (i.e., finding optimal solution) to gain in scalability.

Fig. 10

Computation time cost comparison of ZipLine and its variants. The cost of ZipLine and its variants increases as the number of workers n and the value of parameter R increases. Both ZipLineOpt and ZipLineOptBS outperform the basic ZipLine. For larger values of R ($R \ge 100$), ZipLineOptBS outperforms ZipLineOpt (Color figure online)

6.2 Distributed deep learning using ElasticBSP

We compare the performance of ElasticBSP with BSP, SSP and ASP⁵ by training DNN models from scratch on a parameter server setting. For SSP, we set its threshold parameter to s=3 to ensure it convergences and achieves higher accuracies, as suggested in Ho et al. (2013). For ElasticBSP, we set $R=\{$15, 30, 60, 120, 240$\}$. In case of training large-sized DNN models on large-scale datasets of higher image resolution, we additionally consider $R=\{480, 960\}$. We ran each experiment three times and report the median result of the overall test accuracy.

Platform We implemented ElasticBSP with ZipLineOpt into MXNet (Chen et al., 2015) which supports the BSP and ASP models. The running environment is Ubuntu 16.04.

Cluster Environment We use the GPU cluster maintained by SOSCIP⁶, which consists of 16 IBM POWER8 machines. Each machine has 4 NVIDIA P100 GPUs, 512 GB ram and $2 \times 10$ cores. Each machine connects directly to a switch with 100 Gbps bandwidth (shared by all the 16 machines). Since this GPU cluster is shared by many users from a number of institutions, we are only allowed to use up to 4 machines at a time and each job can only take up to 24 hours. Thus, our experiments were run on 4 IBM POWER8 machines. Note that although this is a homogeneous environment where the speeds of GPUs are the same, the straggler problem still exists in our experiments mainly due to communication delays. Communication delays arise when users’ activities on the network are intensified which fully occupies the switch memory and overloads the CPU of the switch.

Datasets & DNN models We first train a 5-layer convolutional neural networks downsized from AlexNet (Krizhevsky et al., 2012), ResNet-50 and ResNet-100 (He et al., 2016) on two image classification datasets CIFAR-10 and CIFAR-100 (Krizhevsky and Hinton, 2009) with $28 \times 28$ pixels resolution. Then, we move on to train a larger DNN model, VGG-16 (Simonyan and Zisserman, 2014) on the large dataset ImageNet 1K (Deng et al., 2009) with $256 \times 256$ pixels resolution.

Fig. 11

C3F2-Net on CIFAR-10 dataset ($n=4$) (Color figure online)

6.2.1 C3F2-Net on CIFAR-10

Since CIFAR-10 has smaller pixels resolution ($28 \times 28$) than ImageNet 1K, we downsized the AlexNet (8 layers) to a smaller sized neural networks containing 3 convolutional layers and 2 fully connected layers with smaller widths. We name this 5-layer DNN model C3F2-Net to distinguish it from AlexNet⁷.

To train C3F2-Net, we set the mini-batch size to 128, the number of epochs to 400, the learning rate to 0.001 and the weight decay to 0.0005. This setting is the same as the one for AlexNet in (Krizhevsky et al., 2012) except for the learning rate which was set to 0.0001 in (Krizhevsky et al., 2012)⁸. The aforementioned setting is applied to all the distributed synchronization models that we compared with for a fair comparison.

As can be observed in Fig. 11, ElasticBSP converges faster and to higher accuracy than the rest of the synchronization models. BSP converges to a higher accuracy than ASP and SSP, but is slower. Regarding the effect of the parameter R of ElasticBSP, as R increases, ZipLineOpt requires more computation time to determine the optimal synchronization time, for each synchronization barrier imposed. As a result, ElasticBSP with larger R has larger computation cost. This is done without any significant benefit to the accuracy, therefore smaller R values are preferred for smaller models.

Irrelevant to accuracy, the fastest model to finish the 400 epochs is SSP, followed by ASP, ElasticBSP (R={15, 30}) and BSP, meaning that ElasticBSP is faster than BSP due to the reduction in worker waiting time.

Fig. 12

ResNet-50 on CIFAR-100 dataset ($n=4$) (Color figure online)

Fig. 13

ResNet-110 on CIFAR-100 dataset ($n=4$) (Color figure online)

6.2.2 ResNet-50 and ResNet-110 on CIFAR-100

To train a ResNet model, we set the mini-batch size to 128, epoch to 300, learning rate to 0.5, decayed by 10 after epoch 200 for both ResNet-50 and ResNet-110⁹. The results are shown in Figs. 12 and 13. For ResNet-50 in Fig. 12, ElasticBSP converges faster and to a slightly higher accuracy than BSP. Besides, ElasticBSP converges to a slightly higher accuracy than ASP and SSP. ResNet-110 has a similar model size to ResNet-50, but takes much more computing time due to its deeper convolutional layers. Thus, when computation time is long and communication time is relatively short, there is little opportunity to save on communication time during training. As shown in Fig. 13, ElasticBSP converges at a similar rate to BSP, but reaches to slightly higher accuracy. Regarding the effect of the parameter R of ElasticBSP, as R increases to 120, its training time becomes slightly larger than that of BSP due to extra computation time required by ZipLineOpt to compute the time to impose a synchronization barrier.

ASP and SSP converge faster, but require more training time than ElasticBSP and BSP. Recall that ASP and SSP have no bulk synchronization barriers therefore have larger iteration throughput causing faster convergence than ElasticBSP and BSP. But larger iteration throughput introduces more frequent communication between workers and the server, and leads to an increased number of weight updates. Meanwhile, weight updates have to be computed in order (as mentioned in Sect. 2). Thus, their tasks are queued on the server, which introduces extra delay. We further elaborate on this issue in Sect. 6.2.5. A discussion of why ASP and SSP converge faster but take more training time than BSP can be read in Zhao et al. (2019a).

On ResNet models, the faster model to finish the 300 epochs is ElasticBSP, followed by BSP, SSP and ASP. An exception is the ElasticBSP (R={120, 240}), which are slower than BSP on ResNet-110.

6.2.3 VGG-16 on ImageNet 1K

In this experiment, we train VGG-16 on the ImageNet 1K dataset. We used the hyper-parameters setting in the original work (Simonyan & Zisserman, 2014) except for the number of epochs. We set mini-batch size to 256, epoch to 19,¹⁰ learning rate to 0.01, decayed by 5 after epoch 10, 15, 18. Weight decay is set to 0.0005. The results are shown in Fig. 14.

Compared to distributed paradigms with zero staled gradient updates, such as BSP, ElasticBSP converges 1.77$\times$ faster and achieves 12.6% higher final accuracy. Compared to distributed paradigms with staled gradients updates, ElasticBSP is learning faster than SSP and ASP despite the fact that it also has staled gradient updates during training. We also observe that while both SSP and ASP complete the fixed 19 epochs faster than ElasticBSP, they fail to learn. This is due to staled gradients that are constantly present in the training process. Note that for a fixed training time or fixed number of epochs (e.g., 19), ElasticBSP always converges to a higher accuracy than the other synchronization models.

VGG-16 is the largest model size in our analysis, containing 3 fully connected layers (FCLs) that are very sensitive to the staled gradient updates, similarly to the DNNs containing 2 FCLs in Fig. 11 (both have similar learning curves). ASP is unable to learn due to the large number of staled gradients allowed during training. SSP can hardly learn despite it restricts the staleness of its gradients using within a small fixed staleness threshold (e.g., 3).

Since VGG is the largest convolutional neural network model, we experimented with additional two larger values of R for ElasticBSP (i.e., $R=\{480, 960\}$). We wanted to see if increasing the computation time of ZipLine and possibly introducing larger c-staled gradients (introduced by a larger R) might harm the convergence speed and accuracy of ElasticBSP. The results in Fig. 14 show there is only a small variance introduced by the different Rs, meaning that increasing the value of R does not significantly harm the performance of ElasticBSP. This is due to the fact that the computation time of ZipLine is rather negligible compared to the data transmission time of the parameters.

On VGG-16 model, the fastest model to finish the 19 epochs is ASP, followed by SSP, ElasticBSP and BSP. An exception is ElasticBSP (R=15), which is slightly slower than BSP.

Lastly, we add DSSP (Zhao et al., 2019a), which is Dynamic SSP (described in the related work section) for comparison. Figure 14 shows DSSP with the threshold range $s\in [3, 15]$ is better than SSP but is inferior to ElasticBSP.

Fig. 14

VGG-16 on ImageNet 1K dataset ($n=4$) (Color figure online)

6.2.4 ResNet-50 on ImageNet 1K

Having observed the results of ResNet models on the small dataset CIFAR-100 with low pixels resolution in Sect. 6.2.2, we are curious about whether ElasticBSP has the same performance on a large dataset with high pixels resolution when training ResNet-50. In addition, we also include DSSP in the comparison.

The result in Fig. 15 shows that ElasticBSP with different R values have the similar performance as BSP despite a few R values have a slightly faster convergence speed than BSP. This result is consistent with the results in Figs. 12 and 13 in which we observe ResNet-50 has better performance than ResNet-110 in comparison with BSP. As the ratio of communication to computation time decreases, there is less room we can save on the training time. Note that ResNet-110 has 60 more convolutional layers than ResNet-50 which implies its computation time is approximately doubled. Now that we use the ImageNet 1K dataset, the increase of the dimension of the input data also increases the computation time of ResNet-50. In Fig. 12 the dimension of the input data is 784 versus the input data dimension 65,536 in Fig. 15 which sheds light on why ElasticBSP has better performance than BSP on CIFAR-100 than it is on ImageNet 1K for ResNet-50.

To train ResNet-50 on ImageNet 1K, we set the mini-batch size to 256 and epoch to 99 since BSP can complete 99 epochs with the mini-batch size in 24 hours under the testing policy restriction (see the footnote in Sect. 6.2.3). We set learning rate to 0.2, decayed by 10 after epoch 80, 90.¹¹ The aforementioned setting is applied to all the distributed synchronization models for a fair comparison.

In Fig. 15, both ElasticBSP and BSP complete 99 epochs, SSP completes 90 epochs, DSSP completes 82 epochs and ASP completes 78 epochs in 24 hours. We set the staleness threshold s to 3 for SSP and the staleness threshold range $s\in [3, 15]$ for DSSP. We can observe that ElasticBSP and BSP converge to higher accuracy than the others despite DSSP, ASP and SSP converges faster in descending order.

Fig. 15

ResNet-50 on ImageNet 1K dataset ($n=4$) (Color figure online)

6.2.5 Discussion

The results above, run on different sizes of DNN model architectures, provide empirical evidence that ElasticBSP converges to higher accuracy than BSP for large DNNs and can have less training time when R is not too large for the case of small-sized DNNs, and not too small for the case of large-sized DNNs.

In general, ElasticBSP works particularly well on DNNs with fully-connected layers (FCLs). As the size of the DNNs with FCLs grows larger, ElasticBSP shows its superior performance with respect to both convergence speed and accuracy. Note that the variation in the performance of ElasticBSP, BSP, SSP and ASP on different DNNs is expected. The performances of C3F2-Net and VGG-16 are similar to each other, but different from those of ResNets. C3F2-Net contains 2 FCLs and VGG-16 has 3 FCLs, whereas ResNets has no FCLs and therefore fewer model parameters (i.e., smaller size).

Convolutional layers (CVLs) require intensive computing time for matrix dot product operations while computing for FCLs use simple linear algebra operations (Zhao et al., 2019a). Training FCLs requires much less computation time compared to CVLs, while their representation consists of many more parameters than CVLs leading to larger model sizes. On the other hand, training convolutional neural networks without FCLs, such as ResNets, requires much more computing time, but consumes less communication time due to the smaller model size (compared to FCL networks). When the ratio of communication time to computation time is small, there is less room to save on the training time. More detailed analysis of the different behavior on DNNs with different ratios of computation to communication time can be found in Wang and Joshi (2019). In addition, FCLs are sensitive to the staled gradient updates since their representation consists of a large number of parameters (many more than those of CVL representations that consist of shared parameters (Zhao et al., 2019a)). Zhao et al. (2019a) provide a thorough rationale on the different performances of ASP, BSP and SSP on distributed training of various DNN models, with or without FCLs.

In effect, executing parallel SGD using ElasticBSP can be considered as a hybrid model alternating behaviors of an ASP-like and a BSP-like mode: An ASP-like mode occurs during a synchronization period (a superstep $\tau$) and a BSP-like mode occurs across different synchronization barriers b. During the ASP-like mode, staled gradients are generated by the stragglers that harm the convergence, which is traded off for large iteration throughput. At the end of each $\tau$, a BSP-like mode is switched on which eliminates all the staled gradients by imposing a weight synchronization to all workers. Such a periodic clearing of the staled gradients mitigates any significant harm to the convergence. The length of $\tau$ is limited by ZipLine following Corollary 1. Therefore, staled gradients with small staleness values (due to small lengths of $\tau$) function as a regularizer preventing the learned model overfitting the training set.

For DNNs with fully connected layers, we use a moderately small learning rate since a large learning rate (step size) amplifies the staled gradients in all asynchronous parallel models and therefore accelerates the divergence. Nonetheless, this limitation does not affect the practical use of our ElasticBSP in a wide range of DNN models with fully connected layers that require moderately small learning rates. BSP can use a large learning rate since it has zero staled gradients. However, this does not guarantee a faster convergence to a higher accuracy than it uses a moderately small learning rate since the landscape varies on different optimization functions (Wilson and Martinez 2001). A concrete example of moderately small learning rates achieving higher accuracies than large learning rates can be found in Wu et al. (2019).

7 Related work

Several important works closely related to our research have already been cited throughout the manuscript. Here, we discuss more works that try to mitigate the slowdown caused by the straggler problem of BSP which is predominantly adopted in industry. These works use techniques from different areas. For instance, one uses reinforcement learning to find the optimal scheme, one uses a generative model to predict the best synchronization time, and another one uses adaptive learning rates to mitigate the harm of the staled gradients.

Speculative execution to avoid stragglers jobs Chen et al. (2016) deal with the straggler problem by adding k extra backup workers to the distributed training with n workers. In this approach, $k+n$ workers are running to train the model. At each iteration, the server only accepts the gradient updates of the n workers that arrived faster and moves on to the next iteration. The gradients of the k slower workers are dropped. While this approach saves on waiting time (as the n faster workers are needed per iteration), the computing resources allocated to the k slower workers are wasted.

Bayesian prediction for synchronization  Teng and Wood (2018) use a large complex generative model, Bayesian Distributed SGD (BDSGD), to predict the optimal synchronization time or barrier for workers via first predicting the current run-time (iteration interval excluding communication time) of workers based on their historical (run-time) data distributions, and then determine the optimal synchronization barrier according to the predicted workers’ run-times. Yet it follows Chen et al. (2016)’s approach of dropping the gradients of the slower workers that arrive after the predicted optimal synchronization barrier. BDSGD assumes there is a correlation between run-times of workers in each synchronization. Thus, it predicts the current run-time of each worker based on the posterior distributions (i.e., historical run-times of workers). BDSGD requires pre-training on its generative model for the run-time prediction and costs more computing resources per prediction in the actual DNN model training. Consequently, it increases the training time due to its prediction time cost exceeding the workers’ run-time per synchronization. In practice, it has to reuse the result of the synchronization prediction in every few contiguous synchronizations to reduce the frequency of running the learned generative prediction model. BDSGD converges to a similar accuracy as BSP with its complex prediction model. Our ElasticBSP converges to a significantly higher accuracy than BSP on large DNNs despite it uses a greedy algorithm to solve the optimization problem.

Sparse synchronizations EASGD (Zhang et al., 2015) first proposed to reduce the communication cost by allowing the workers to update weights locally per iteration and to synchronize with the server only at a fixed communication period. However, with fewer synchronizations, the divergence among local models can result in an error-convergence (Wang and Joshi 2019). ADACOMM (Wang & Joshi, 2019) uses periodic-averaging SGD (PASGD) for bulk synchronization in which workers are doing local updates for $\tau$ iterations before a weight synchronization. That way, the communication cost of both uploading gradients and downloading weights from the server occurs only once every $\tau$ iterations. In practice, ADACOMM estimates the optimal $\tau$ for a bulk synchronization of local weights based on the training loss, but does not address the straggler problem. In contrary to ADACOMM’s approach of assigning the same $\tau$ to all workers, our ElasticBSP predicts the optimal synchronization time for all workers, where each worker can have a different $\tau$.

Auto-synchronization-RL  Zhu et al. (2020) proposed to address the straggler problem using reinforcement learning (RL) in full automation by formulating the synchronization policy as a RL problem. By using the deep Q-learning algorithm (Van Hasselt et al., 2016), the learned RL policies were able to speedup the training process on shallow DNNs and small datasets. Yet the authors admitted that the work has its limitations and it is not ready for the real-world scenario. Our ElasticBSP uses the lightweight but effective greedy algorithm to minimize the waiting time caused by the stragglers. Therefore, we save the time cost of a few episodes required by RL on training the RL model to learn the policies before it can be deployed to the actual DNNs training. Besides, ElasticBSP demonstrates outstanding performance on large DNNs and large datasets.

Auto-synchronization-DL Recently, Zhang et al. (2020) proposed AutoSync which automatically optimizes the synchronization policies by first learning the representation of the target DNN models (to be trained) and the resource specifications (e.g., the networking topology of the cluster, the messaging partitioning and communication) using a few hundreds of trail runs on a neural based simulator, and then starting to discover the optimal synchronization policy based on the learned simulator. The neural based simulator can be a linear model, a recurrent neural network or a graph attention network. Unlike the RL approach, AutoSync builds the fine-grained machine learning based pipeline to search the optimal synchronization strategy. AutoSync uses the similar synchronization cost model as our ElasticBSP to measure the synchronization time per iteration, and the similar approach to estimate an iteration interval of a worker. But these pieces of information are vectorized as a part of the representation feeding to the neural based simulator in AutoSync training. On the other hand, ElasticBSP utilizes them directly in the lightweight greedy algorithm to find the optimal synchronization time. Similar to the RL approach, AutoSync requires extra training time for its neural based simulator to learn the representation of the target DNN model and the resource specifications. On the contrary, ElasticBSP can be used directly to train DNN models without additional time cost and computing resources.

Dynamic soft synchronization Other than BSP, the straggler problem also exists in SSP despite that SSP was devised to solve the straggler problem in BSP. DSSP (Zhao et al. 2019a) introduces the dynamic staleness threshold to minimize the waiting time for SSP, which uses a fixed staleness threshold. By predicting the future iterations for the fastest and the slowest workers based on their most recent iterations, DSSP finds the optimal staleness threshold between pre-defined lower and upper thresholds of SSP per iteration for the fastest workers at run time to minimize the waiting time of the fastest workers. The prediction of the future R iterations of workers based on their most recent iteration history is also used in our ElasticBSP. In our experiments, we demonstrated that ElasticBSP is superior to DSSP in terms of accuracy.

Adjusting the learning rate of staled gradients Dutta et al. (2018) promoted asynchrony (i.e., ASP) and provided a thorough analysis on the parallel SGD with and without synchronization. They proposed an adaptive learning rate scheme to accelerate the convergence speed in wall-clock time for ASP. Similar to ElasticBSP, they measure iteration intervals (processing time) by using the consecutive push timestamps of each worker. In Dutta et al. (2018), the harm that the staled gradients bring to the convergence was diminished by tuning down the learning rate according to the staleness value of the weight parameters at run time on the parameter server side. However, the tuning process is expensive on the computing resources for large DNNs and not scalable when the number of workers increases, since it requires the server to always keep a copy of the recently read weight parameters for every worker. The authors also confirm that the synchronization is critical to the convergence speed and aim to increase the synchronization frequency in the future.

8 Conclusions

In this paper, we proposed ElasticBSP for distributed DNN model training, using the parameter server framework. Our model is orthogonal to other types of DNN training optimizations. ElasticBSP is relaxing the bulk synchronization requirement of BSP and allows asynchronous gradient updates to a certain extent to ensure the quality of convergence and achieve higher accuracy. As a result, it increases the iteration throughput of the workers, limits the staled gradients to a small amount and their staleness values to a small number, which brings less harm to the convergence (Ho et al., 2013). ElasticBSP operates in two phases. First, R future iterations of each worker are predicted. Then, ZipLine (or any of its variants) is applied to determine the time to impose the next synchronization barrier that minimizes the overall workers’ waiting time. ZipLine is a one-pass algorithm with linearithmic complexity ${\mathcal {O}}(Rn\log {}n)$ and adds a minimal overhead on the server, so it can be easily ported on popular distributed machine learning frameworks. The experimental results show that with a right value of R (tunable) for the size of the DNN model, ElasticBSP provides faster convergence than BSP for a number of DNNs while achieving higher (or comparable) accuracy than other state-of-the-art synchronization models in the parameter server setting, including ASP, SSP and BSP, on different datasets. Overall, our work provides theoretical and empirical evidence that ElasticBSP offers a better alternative.