1 Introduction

In various applications in economics, engineering, medicine, physics, and several other fields, one has often the need of approximating a function, based on a finite set of input/output noisy examples. This belongs to the typical class of problems investigated by supervised machine learning (Hastie et al. 2009; Vapnik 1998). In some cases, the noise variance of the output variable can be decreased, at least to some extent, by making the cost of each supervision larger. As an example, observations could be acquired by using more precise measurement devices (then, likely, having also larger acquisition cost). Similarly, each supervision could be made by an expert (also in this case, a larger cost would be expected by increasing the level of expertise). In all these situations, it can be useful to optimize the trade-off between the training set size and the precision of supervision. In the conference work Gnecco and Nutarelli (2019), this kind of analysis was conducted by proposing a modification of the classical linear regression model, in which one has the additional possibility to control the conditional variance of the output variable given the associated input variables, by changing the time (hence, the cost) dedicated to provide a label to each training input example, and fixing an upper bound on the time available for the supervision of the whole training set. Based on a large-sample approximation of the output of the ordinary least squares regression algorithm, it was shown in that work that the optimal choice of the supervision time per example highly depends on how the precision of supervision scales with respect to the cost per training example. The analysis was refined in Gnecco and Nutarelli (2019), where a related optimization problem, based on the analysis of the output produced by a different regression algorithm (namely, weighted least squares) was considered, obtaining similar results at optimality, for a model in which distinct training examples are possibly associated with different supervision times. Finally, in the conference work Gnecco and Nutarelli (2020), the analysis of the optimal trade-off between training set size and precision of supervision was extended to a more general linear model of the input/output relationship, namely, the fixed effects panel data model. In this model, observations associated with different units (individuals) depend also on additional constants, one for each unit, which make it possible to include, in the input/output relationship, unobserved heterogeneity in the data. Moreover, each unit is observed along another dimension, which is typically time. This kind of model (and its variations) is commonly applied in the analysis of data in both microeconomics and macroeconomics (Arellano 2004; Cameron and Trivedi 2005; Wooldridge 2002), where each unit may represent, for instance, a firm, or a country. It is also applied in biostatistics (Härdle et al. 2007) and sociology (Frees 2004). An important engineering application of the model (and of its variations) is in the calibration of sensors (Reeve 1988, Sect. 4.1).

In order to increase the applicability of the analysis carried out in our previous conference work (Gnecco and Nutarelli 2020), in this paper we extend it thoroughly in the following directions. First, Gnecco and Nutarelli (2020) investigated only the case in which the measurements errors of observations associated with the same unit are mutually independent. In this paper, we extend such analysis to the case of dependent measurement errors. Moreover, differently from Gnecco and Nutarelli (2020), we confirm the validity of the obtained theoretical results numerically. Further, in Gnecco and Nutarelli (2020), the optimal trade-off between training set size and precision of supervision was analyzed only for a fixed number of units, assuming that the number of observations associated with the same unit is large enough to justify a large-sample approximation with respect to the number of observations. In the last part of this work, we consider additionally the cases of a large-sample approximation with respect to the number of units, and of a large-sample approximation with respect to both the number of units and the number of observations per unit.

In line with the results of the theoretical analyses made in (Gnecco and Nutarelli 2019, 2019, 2020) for simpler linear regression models, we show that, also for the more applicable fixed effects generalized least squares panel data model, the following holds in general: when the precision of each supervision (i.e., the reciprocal of the conditional variance of the output variable, given the associated unit and input variables) increases less than proportionally versus an increase of the supervision cost per training example, the minimum (large-sample approximation of the) generalization error (conditioned on the training input data) is obtained in correspondence of the smallest supervision cost per example (hence, of the largest number of examples); when that precision increases more than proportionally versus an increase of the supervision cost per example, the optimal supervision cost per example is the largest one (which corresponds to the smallest number of examples). Differently from (Gnecco and Nutarelli 2019, 2019, 2020), in the analysis made in the present work, the number of training examples can be varied either by increasing the number of observations per unit, or the number of units, or both. In summary, the results of the analyses made in (Gnecco and Nutarelli 2019, 2019, 2020) and, for a different and more complex regression model, in this paper, highlight that increasing the training set size is not always beneficial, if a smaller number of more reliable data can be collected. Hence, not only the quantity of data, but of course, also their quality matters. This looks particularly relevant when the data collection process can be designed before data are actually collected.

The paper is structured as follows. Section 2 provides a background on the fixed effects generalized least squares panel data model. Section 3 presents the analysis of its conditional generalization error, and of the large-sample approximation of the latter with respect to time. Section 4 formulates and solves an optimization problem we propose in order to provide an optimal trade-off between training set size and precision of supervision for the fixed effects generalized least squares panel data model, using the large-sample approximation above. Section 5 presents some numerical results, which validate the theoretical ones. Finally, Sect. 6 discusses some possible applications and extensions of the theoretical results obtained in the work. Some technical proofs and remarks about the extension of the analysis made in the paper to other large-sample settings are reported in the Appendices.

2 Background

In this section, we recall some basic facts about the following Fixed Effects Generalized Least Squares (FEGLS) panel data model (see, e.g., Wooldridge 2002, Chapter 10). Specifically, we refer to the following model:

$$\begin{aligned} y_{n,t}:=\eta _n+\underline{\beta }'{\underline{x}}_{n,t}, \,\,{\mathrm{for}}\,\, n=1,\ldots ,N,t=1,\ldots ,T\,, \end{aligned}$$
(1)

where the outputs \(y_{n,t} \in {\mathbb {R}}\) are scalars, whereas the inputs \({\underline{x}}_{n,t}\) (\(n=1,\ldots ,N,t=1,\ldots ,T\)) are column vectors in \({\mathbb {R}}^p\), and are modeled as random vectors. The superscript \('\) denotes transposition. The parameters of the model are the individual constants \(\eta _n\) (\(n=1,\ldots ,N)\), one for each unit, and the column vector \(\underline{\beta }\in {\mathbb {R}}^p\). The constants \(\eta _n\) are also called fixed effects. Eq. (1) represents a balanced panel data model, in which each unit n is associated with the same number T of outputs, each one at a different time t. The model represents the case in which the input/output relationship is linear, and different units, which are observed at the times \(t=1,\ldots ,T\), are associated with possibly different constants.

Note that the outputs \(y_{n,t}\) are actually unavailable; only their noisy measurements \(z_{n,t}\) can be obtained, which are assumed to be generated according to the following additive noise model:

$$\begin{aligned} z_{n,t}:=y_{n,t}+\varepsilon _{n,t}\,,\,\,{\mathrm{for}}\,\, n=1,\ldots ,N,t=1,\ldots ,T\,, \end{aligned}$$
(2)

where, for any n, the \(\varepsilon _{n,t}\) are identically distributed and possibly dependent random variables, having mean 0, and are further independent from all the \({\underline{x}}_{n,t}\). For any two units \(n \ne m\) and any two time instants \(t_1,t_2 \in \{1,\ldots ,T\}\), \(\varepsilon _{n,t_1}\) and \(\varepsilon _{m,t_2}\) are assumed to be independent. Hence, only the possibility of temporal dependence for the measurement errors associated with the same unit is considered in the following, in line with several works in the literature (see, e.g., Bhargava et al. (1982) and (Wooldridge 2002, Section 10.5.5)).

For each unit n, let \(X_n \in {\mathbb {R}}^{T \times p}\) be the matrix whose rows are the transposes of the \({\underline{x}}_{n,t}\); further, let \({\underline{z}}_n \in {\mathbb {R}}^T\) be the column vector which collects the noisy measurements \(z_{n,t}\), and \(\underline{\varepsilon }_n \in {\mathbb {R}}^T\) the column vector which collects the measurement noises \(\varepsilon _{n,t}\). The input/corrupted output pairs \(({\underline{x}}_{n,t},{\underline{z}}_{n,t})\), for \(n=1,\ldots ,N\), \(t=1,\ldots ,T\), are used to train the FEGLS model, i.e., to estimate its parameters.

The following first-order serial covariance form is assumed (see, e.g., Bhargava et al. (1982) and Wooldridge (2002, Section 10.5.5)) for the (unconditional) covariance matrix of the vector of measurement noises associated with the n-th unitFootnote 1, where \(\sigma > 0\) and \(\rho \in (-1,1)\) hold (here, \({\mathbb {E}}\) denotes the expectation operator):

$$\begin{aligned} {\varLambda := \sigma ^2 \varPsi := {\mathrm{Var}}\left( \underline{\varepsilon }_n\right) ={\mathbb {E}}\{\underline{\varepsilon }_n \underline{\varepsilon }_n'\} =} \sigma ^2 {\begin{bmatrix} 1 &{} \rho &{} \rho ^2 &{} \cdots &{} \rho ^{T-2} &{} \rho ^{T-1} \\ \rho &{} 1 &{} \rho &{} \rho ^2 &{} \cdots &{} \rho ^{T-2} \\ \rho ^2 &{} \rho &{} 1 &{} \rho &{} \cdots &{} \rho ^{T-3} \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ \rho ^{T-1} &{} \rho ^{T-2} &{} \cdots &{} \rho ^2 &{} \rho &{} 1 \end{bmatrix}}\,\in {\mathbb {R}}^{T \times T}\,, \end{aligned}$$
(3)

which is a symmetric and positive-definite matrix. In other words, the measurement noise is assumed to be generated by a first-order autoregressive (AR(1)) process (Ruud 2000, Section 25.2). In the particular case of uncorrelated (\(\rho =0\)) and independent measurement noises, one obtains the model considered in Gnecco and Nutarelli (2020).

Let the matrix \(Q_T \in {\mathbb {R}}^{T \times T}\) be defined as

$$\begin{aligned} Q_T:=I_T-\frac{1}{T} {\underline{1}}_T {\underline{1}}_T'\,, \end{aligned}$$
(4)

where \(I_T \in {\mathbb {R}}^{T \times T}\) is the identity matrix, and \({\underline{1}}_T \in {\mathbb {R}}^T\) a column vector whose elements are all equal to 1. One can check that \(Q_T\) is a symmetric and idempotent matrix (i.e., \(Q_T'=Q_T=Q_T^2\)), and its eigenvalues are 0 with multiplicity 1, and 1 with multiplicity \(T-1\). Hence, for each unit n, one can define

$$\begin{aligned} {\ddot{X}}_n:= & {} Q_T X_n= \begin{bmatrix} {\underline{x}}_{n,1}-\frac{1}{T}\sum _{t=1}^T {\underline{x}}_{n,t} \\ {\underline{x}}_{n,2}-\frac{1}{T}\sum _{t=1}^T {\underline{x}}_{n,t} \\ \cdots \\ {\underline{x}}_{n,T}-\frac{1}{T}\sum _{t=1}^T {\underline{x}}_{n,t} \end{bmatrix}\,, \end{aligned}$$
(5)
$$\begin{aligned} \underline{\ddot{z}}_n:= & {} Q_T {\underline{z}}_n= \begin{bmatrix} z_{n,1}-\frac{1}{T}\sum _{t=1}^T z_{n,t} \\ z_{n,2}-\frac{1}{T}\sum _{t=1}^T z_{n,t} \\ \cdots \\ z_{n,T}-\frac{1}{T}\sum _{t=1}^T z_{n,t} \end{bmatrix} \,, \end{aligned}$$
(6)

and

$$\begin{aligned} \underline{\ddot{\varepsilon }}_n := Q_T \underline{\varepsilon }_n= \begin{bmatrix} \varepsilon _{n,1}-\frac{1}{T}\sum _{t=1}^T \varepsilon _{n,t} \\ \varepsilon _{n,2}-\frac{1}{T}\sum _{t=1}^T \varepsilon _{n,t} \\ \cdots \\ \varepsilon _{n,T}-\frac{1}{T}\sum _{t=1}^T \varepsilon _{n,t} \end{bmatrix} \,, \end{aligned}$$
(7)

which represent, respectively, the matrix of time de-meaned training inputs, the vector of time de-meaned corrupted training outputs, and the vector of time de-meaned measurements noises. The goal of time de-meaning is to obtain a derived dataset where the fixed effects are removed, making it possible to estimate first the vector \(\underline{\beta }\), then - turning back to the original dataset - the fixed effects \(\eta _n\). The covariance matrix \({\mathbb {E}}\{\ddot{\underline{\varepsilon }}_n\ddot{\underline{\varepsilon }}_n'\}\) has the expression

$$\begin{aligned} {\varOmega :=\sigma ^2\varPhi :={\mathrm{Var}}\left( \ddot{\underline{\varepsilon }}_n\ddot{\underline{\varepsilon }}_n'\right) }={\mathbb {E}}\{\ddot{\underline{\varepsilon }}_n\ddot{\underline{\varepsilon }}_n'\}=Q_T {\mathbb {E}}\{\underline{\varepsilon }_n \underline{\varepsilon }_n'\}Q_T'=Q_T \varLambda Q_T'={\sigma ^2 Q_T \varPsi Q_T'}\,, \end{aligned}$$
(8)

which is symmetric and positive semi-definite, and has rank \(T-1<T\) (Wooldridge 2002). Although this deficient rank prevents the application of the most usual approach to Generalized Least Squares (GLS) estimation, based on the inversion of the covariance matrix \(\varOmega\) (which in this case cannot be inverted), one can still apply GLS by projecting Eqs. (1) and (2) onto the orthogonal complement L of the vector \({\underline{1}}_T\) by using \(Q_T\), then solving a standard GLS problem on L (Aitken 1936). This is formally obtained by replacing the inverse of the covariance matrix with its Moore-Penrose pseudoinverseFootnote 2 (denoted by \(\varOmega ^+\)), as made in the context of FEGLS estimation in Kiefer (1980, Im et al. (1999). More precisely, assuming the invertibility of the matrix \(\sum _{n=1}^N {{\ddot{X}}_n' {\varOmega ^{+}} {\ddot{X}}_n}\) (see Remark 3.1 for a justification of this assumption), the FEGLS estimate of \(\underline{\beta }\) is

$$\begin{aligned} \underline{\hat{\beta }}_{FEGLS}= & {} \left( \sum _{n=1}^N {{\ddot{X}}_n' \varOmega ^{+} {\ddot{X}}_n} \right) ^{-1} \left( \sum _{n=1}^N {{\ddot{X}}_n' \varOmega ^{+} \underline{\ddot{z}}_n}\right) \,. \end{aligned}$$
(9)

The estimate \(\underline{\hat{\beta }}_{FEGLS}\) in (9) can be interpreted as the GLS estimate of \(\underline{\beta }\) obtained by replacing the original input/corrupted output training data with their de-meaned versions reported above. It is worth observing that the training input/corrupted output pairs \(\left( {\underline{x}}_{n,t},z_{n,t}\right)\) (\(n=1,\ldots ,N,t=1,\ldots ,T\)) are all used to estimate \(\underline{\beta }\).

Remark 2.1

Another commonly used approach to deal with the issue above is to drop one of the time periods from the analysis, in order to get an invertible covariance matrix. It can be rigorously proved (see, e.g. (Im et al. 1999, Theorem 4.3)) that this second approach is equivalent to the one based on the Moore-Penrose pseudoinverse (producing exactly the same FEGLS estimate), and that it does not matter which time period is dropped, as the resulting GLS estimator has always the same form. Therefore, dropping the last row of \(Q_T\), one gets the matrix \({\tilde{Q}}_T \in {\mathbb {R}}^{(T-1)\times T}\), from which one obtains the matrix \(\tilde{{\ddot{X}}}_n := {\tilde{Q}}_T X_n \in {\mathbb {R}}^{(T-1) \times p}\), the column vector \(\tilde{\ddot{{\underline{z}}}}_n := {\tilde{Q}}_T {\underline{z}}_n \in {\mathbb {R}}^{T-1}\), and the column vector \(\tilde{\ddot{\underline{\varepsilon }}}_n:= {\tilde{Q}}_T \underline{\varepsilon }_n \in {\mathbb {R}}^{T-1}\). Moreover, denoting by \({\tilde{X}}_n \in {\mathbb {R}}^{(T-1) \times p}\), \(\tilde{{\underline{z}}}_n \in {\mathbb {R}}^{T-1}\), and \(\tilde{\underline{\varepsilon }}_n \in {\mathbb {R}}^{T-1}\) the matrix and the vectors obtained by removing the last row, respectively, from \(X_n\), \({\underline{z}}_n\), and \(\underline{\varepsilon }_n\), one gets

$$\begin{aligned} {\tilde{\varOmega }} := {\mathbb {E}}\{\tilde{\ddot{\underline{\varepsilon }}}_n\tilde{\ddot{\underline{\varepsilon }}}_n'\} = {\tilde{Q}}_T{\mathbb {E}}\{\underline{\varepsilon }_n \underline{\varepsilon }_n'\}{\tilde{Q}}_T' = {\tilde{Q}}_T \varLambda {\tilde{Q}}_T'\,, \end{aligned}$$
(10)

which is, differently from \(\varOmega\), an invertible matrix, with inverse \({\tilde{\varOmega }^{-1}} = ({\tilde{Q}}_T \varLambda {\tilde{Q}}_T')^{-1}\). The resulting FEGLS estimate is

$$\begin{aligned} \underline{\hat{\beta }}_{FEGLS}^{alt}= & {} \left( \sum _{n=1}^N \tilde{{\ddot{X}}}_n' {\tilde{\varOmega }^{-1}} \tilde{{\ddot{X}}}_n\right) ^{-1} \left( \sum _{n=1}^N \tilde{{\ddot{X}}}_n' {\tilde{\varOmega }^{-1}} \tilde{\underline{\ddot{z}}}_n\right) \,. \end{aligned}$$
(11)

(see, e.g., Wooldridge (2002)). The FEGLS estimate \(\underline{\hat{\beta }}_{FEGLS}\) and the alternative one \(\underline{\hat{\beta }}_{FEGLS}^{alt}\) are actually identical (Im et al. 1999, Theorem 4.3). This equivalence is obtained by expressing such estimates in terms of the original variables before de-meaning, then exploiting the proof of (Im et al. 1999, Theorem 4.3), which shows that \(Q_T'\varOmega ^{+} Q_T={\tilde{Q}}_T' \tilde{\varOmega }^{-1} {\tilde{Q}}_T\) (this still holds if an observation different from the last one is dropped, and \({\tilde{Q}}_T\) is redefined accordingly).

The FEGLS estimates of the \(\eta _n\) (also called fixed effects residuals (Wooldridge 2002)) are

$$\begin{aligned} \hat{\eta }_{n,FEGLS}:=\frac{1}{{T}} \sum _{t=1}^{{T}} \left( z_{n,t}-\underline{\hat{\beta }}_{FEGLS}'{\underline{x}}_{n,t}\right) \,. \end{aligned}$$
(12)

They are obtained by subtracting the estimate \(\underline{\hat{\beta }}_{FEGLS}'{\underline{x}}_{n,t}\) of \(\underline{\beta }'{\underline{x}}_{n,t}\) from each corrupted output \(z_{n,t}\), then performing an empirical average, limiting to training data associated with the unit n. The FEGLS estimates reported in Eq. (12) are motivated by the fact that the \(\eta _n\) are constants, whereas the \(\varepsilon _{n,t}\) have mean 0.

By taking expectations, it readily follows from their definitions that the estimates (9) and (12) are conditionally unbiased with respect to the training input data \(\{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}\), i.e., that

$$\begin{aligned} {\mathbb {E}} \left\{ \left( \underline{\hat{\beta }}_{FEGLS}-\underline{\beta }\right) |\{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}\right\} ={\underline{0}}_p\,, \end{aligned}$$
(13)

where \({\underline{0}}_p \in {\mathbb {R}}^p\) is a column vector whose elements are all equal to 0, and, for any \(i=1,\ldots ,N\),

$$\begin{aligned} {\mathbb {E}} \left\{ \left( \hat{\eta }_{i,FEGLS}-\eta _{i}\right) |\{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}\right\} =0\,. \end{aligned}$$
(14)

Finally, the covariance matrix of \(\underline{\hat{\beta }}_{FEGLS}\), conditioned on the training input data, is

$$\begin{aligned} {\mathrm{Var}}\left( \underline{\hat{\beta }}_{FEGLS}|\{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}\right)= & {} \left( \sum _{n=1}^N {{\ddot{X}}_n' \varOmega ^{+} {\ddot{X}}_n} \right) ^{-1}\,. \end{aligned}$$
(15)

3 Conditional generalization error and its large-sample approximation

The goal of this section is to analyze the generalization error associated with the FEGLS estimates (9) and (12), conditioned on the training input data, by providing its large-sample approximation. Then, in Sect. 4, the resulting expression is optimized, after choosing suitable models for the standard deviation \(\sigma\) of the measurement noise and for the time horizon, which is chosen in such a way it satisfies a suitable budget constraint.

First, we express the generalization error or expected risk for the i-th unit (\(i=1,\ldots ,N\)), conditioned on the training input data, by

$$\begin{aligned} {R_i\left( \{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}\right) :=} {\mathbb {E}} \left\{ \left( \hat{\eta }_{i,FEGLS}+\underline{\hat{\beta }}_{FEGLS}'{\underline{x}}_i^{test}-\eta _i-\underline{\beta }'{\underline{x}}_i^{test}\right) ^2 \big | \{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}\right\} \,, \end{aligned}$$
(16)

where \({\underline{x}}_i^{test} \in {\mathbb {R}}^p\) is independent from the training data. It is the expected mean squared error of the prediction of the output associated with a test input, conditioned on the training input data.

As shown in Appendix 1, we can express the conditional generalization error (16) as follows, highlighting its dependence on \(\sigma ^2\):

$$\begin{aligned}&{R_i\left( \{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}\right) } \nonumber \\&\quad =\frac{\sigma ^2}{{T}^2} {\underline{1}}_{{T}}' {X_i} \left( \sum _{n=1}^N {{\ddot{X}}_n'\varPhi ^{+} {\ddot{X}}_n}\right) ^{-1} {X_i'} {\underline{1}}_{{T}} +\frac{\sigma ^2}{{T}^2}{\underline{1}}_{{T}}' {\varPsi } {\underline{1}}_{{T}} \nonumber \\&\qquad -\frac{2 {\sigma ^2}}{{T}^2} {\underline{1}}_{{T}}' {X_i} \left( \sum _{n=1}^N {{\ddot{X}}_n'\varPhi ^{+} {\ddot{X}}_n} \right) ^{-1} {{\ddot{X}}_i'\varPhi ^{+} Q_T} {\varPsi } {\underline{1}}_{{T}} + \sigma ^2 {\mathbb {E}} \Bigg \{\left( {\underline{x}}_i^{test}\right) '\left( \sum _{n=1}^N {{\ddot{X}}_n'\varPhi ^{+} {\ddot{X}}_n} \right) ^{-1} {\underline{x}}_i^{test} {\big | \{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}} \Bigg \} \nonumber \\&\qquad -\frac{2 \sigma ^2}{{T}} {\underline{1}}_{{T}}' {X_i} \left( \sum _{n=1}^N {{\ddot{X}}_n'\varPhi ^{+} {\ddot{X}}_n}\right) ^{-1} {\mathbb {E}} \left\{ {\underline{x}}_i^{test} \right\} +\frac{2 {\sigma ^2}}{{T}} \left( {Q_T} {\varPsi } {\underline{1}}_{{T}}\right) ' {\varPhi ^{+} {\ddot{X}}_i} \left( \sum _{n=1}^N {{\ddot{X}}_n' \varPhi ^{+} {\ddot{X}}_n} \right) ^{-1} {\mathbb {E}} \left\{ {\underline{x}}_i^{test} \right\} \,, \end{aligned}$$
(17)

where some computations (reported in Appendix 1) show that

$$\begin{aligned} {\underline{1}}_{{T}}' {\varPsi } {\underline{1}}_{{T}}={T+2T\bigg (\frac{1-\rho ^{T}}{1-\rho }-1\bigg )-\frac{2 \rho }{1-\rho } \big (-(T-1)\rho ^{T-1}+\rho ^{T-2}+\rho ^{T-3}+\dots +1\big )}\,, \end{aligned}$$
(18)

and

$$\begin{aligned} {{\underline{v}}_T}&{:=} \,{Q_T} {\varPsi } {\underline{1}}_{{T}} \nonumber \\= & {} {\begin{bmatrix} \not \!{1} + \rho +\rho ^2+ \rho ^3 + \rho ^4 + \cdots &{} + \rho ^{T-1} &{} \big /\!\!\!\!\!\!\!{-1}-2\frac{1-\rho ^T}{1-\rho }+2+\frac{2\rho [-(T-1)\rho ^{T-1}+\rho ^{T-2}+\rho ^{T-3}+\dots +1]}{T(1-\rho )} \\ \rho + \not \!{1} + \rho +\rho ^2+ \rho ^3 + \cdots &{} + \rho ^{T-2} &{} \big /\!\!\!\!\!\!\!{-1}-2\frac{1-\rho ^T}{1-\rho }+2+\frac{2\rho [-(T-1)\rho ^{T-1}+\rho ^{T-2}+\rho ^{T-3}+\dots +1]}{T(1-\rho )} \\ \rho ^2 +\rho + \not \!{1} + \rho +\rho ^2+ \cdots &{} + \rho ^{T-3} &{} \big /\!\!\!\!\!\!\!{-1}-2\frac{1-\rho ^T}{1-\rho }+2+\frac{2\rho [-(T-1)\rho ^{T-1}+\rho ^{T-2}+\rho ^{T-3}+\dots +1]}{T(1-\rho )} \\ \cdots &{} \cdots &{} \cdots \\ \rho ^{T-3} + \rho ^{T-4} + \cdots + \rho + \not \!{1} + \rho &{} + \rho ^{2} &{} \big /\!\!\!\!\!\!\!{-1}-2\frac{1-\rho ^T}{1-\rho }+2+\frac{2\rho [-(T-1)\rho ^{T-1}+\rho ^{T-2}+\rho ^{T-3}+\dots +1]}{T(1-\rho )} \\ \rho ^{T-2} + \rho ^{T-3} + \cdots + \rho ^2 + \rho + \not \!{1} &{} +\rho &{} \big /\!\!\!\!\!\!\!{-1}-2\frac{1-\rho ^T}{1-\rho }+2+\frac{2\rho [-(T-1)\rho ^{T-1}+\rho ^{T-2}+\rho ^{T-3}+\dots +1]}{T(1-\rho )} \\ \rho ^{T-1} + \rho ^{T-2} + \cdots + \rho ^3 + \rho ^2 +\rho &{} + \not \!{1} &{} \big /\!\!\!\!\!\!\!{-1}-2\frac{1-\rho ^T}{1-\rho }+2+\frac{2\rho [-(T-1)\rho ^{T-1}+\rho ^{T-2}+\rho ^{T-3}+\dots +1]}{T(1-\rho )} \end{bmatrix}}\,. \end{aligned}$$
(19)

Next, we obtain a large-sample approximation of the conditional generalization error (17) with respect to T, for a fixed number of units N. Such an approximation is useful, e.g., in the application of the model to macroeconomics data, for which it is common to investigate the case of a large horizon T.

Under mild conditions (e.g., if for the unit i the \({\underline{x}}_{i,t}\) are mutually independent, identically distributed, and have finite moments up to the order 4), the following convergences in probabilityFootnote 3 hold (their proofs are reported in Appendix 2):

$$\begin{aligned}&\underset{T \rightarrow +\infty }{\mathrm{plim}} \frac{1}{T} {\underline{1}}_{T}' {X}_i= \left( {\mathbb {E}} \left\{ {\underline{x}}_{i,1}\right\} \right) '\,, \end{aligned}$$
(20)
$$\begin{aligned}&\underset{T \rightarrow +\infty }{\mathrm{plim}} \frac{1}{T} {{\ddot{X}}_i'\varPhi ^{+} Q_T} {\varPsi } {\underline{1}}_{T} = {\underline{0}}_p\,. \end{aligned}$$
(21)

Similarly, if for each fixed unit n the \({\underline{x}}_{n,t}\) are mutually independent, identically distributedFootnote 4, and have finite moments up to the order 4, and one makes the additional assumption (whose validity is discussed extensively in Appendix 2) that

$$\begin{aligned} \underset{T \rightarrow \infty }{\lim }\Vert \varPhi ^+-Q_T \varPsi ^{-1} Q_T'\Vert _2=0 \end{aligned}$$
(22)

(where, for a symmetric matrix \(M \in {\mathbb {R}}^{T \times T}\), \(\Vert M\Vert _2=\underset{t=1,\ldots ,T}{\max }|\lambda _t(M)|\) denotes its spectral norm), then also the following convergence in probability holds:

$$\begin{aligned} \underset{T \rightarrow +\infty }{\mathrm{plim}} \frac{1}{T} \sum _{n=1}^N {{\ddot{X}}_n' \varPhi ^{+} {\ddot{X}}_n}=A_N\,, \end{aligned}$$
(23)

where

$$\begin{aligned} A_N=A_N':= \frac{1+\rho ^2}{1-\rho ^2} \sum _{n=1}^N {\mathbb {E}} \left\{ \left( {\underline{x}}_{n,1}-{\mathbb {E}} \left\{ {\underline{x}}_{n,1}\right\} \right) \left( {\underline{x}}_{n,1}-{\mathbb {E}} \left\{ {\underline{x}}_{n,1}\right\} \right) '\right\} \end{aligned}$$
(24)

is a symmetric and positive semi-definite matrix. In the following, its positive definiteness (hence, its invertibility) is also assumed.

Remark 3.1

The existence of the probability limit (23) and the assumed positive definiteness of the matrix \(A_N\) guarantee that the invertibility of the matrix \(\sum _{n=1}^N {{\ddot{X}}_n' \varPhi ^{+} {\ddot{X}}_n}\) (see the invertibility assumption before Eq. (9)) holds with probability near 1 for large T.

When (20), (21), and (23) hold, inserting such probability limits in Eq. (17), one gets the following large-sample approximation of the conditional generalization error (17) with respect to T:

$$\begin{aligned} (17)\simeq & {} \frac{\sigma ^2}{T} \left( {\mathbb {E}} \left\{ {\underline{x}}_{i,1}\right\} \right) ' A_N^{-1} {\mathbb {E}} \left\{ {\underline{x}}_{i,1}\right\} +\frac{\sigma ^2}{T} \frac{1+\rho }{1-\rho }\nonumber \\&\quad +\frac{\sigma ^2}{T} {\mathbb {E}} \left\{ \left( {\underline{x}}_i^{test}\right) ' A_N^{-1} {\underline{x}}_i^{test} \right\} -2 \frac{\sigma ^2}{T} \left( {\mathbb {E}} \left\{ {\underline{x}}_{i,1}\right\} \right) ' A_N^{-1} {\mathbb {E}} \left\{ {\underline{x}}_i^{test} \right\} \nonumber \\= & {} \frac{\sigma ^2}{T} \left( \frac{1+\rho }{1-\rho } + {\mathbb {E}} \left\{ \left\| A_N^{-\frac{1}{2}} \left( {\mathbb {E}} \left\{ {\underline{x}}_{i,1}\right\} -{\underline{x}}_i^{test}\right) \right\| _2^2\right\} \right) \,, \end{aligned}$$
(25)

where, for a vector \({\underline{v}} \in {\mathbb {R}}^p\), \(\Vert {\underline{v}}\Vert _2\) denotes its \(l_2\) (Euclidean) norm, and \(A_N^{-\frac{1}{2}}\) is the principal square root (i.e., the symmetric and positive definite square root) of the symmetric and positive definite matrix \(A_N^{-1}\). Eq. (25) is obtained taking into account that, as a consequence of the Continuous Mapping Theorem (Florescu 2015, Theorem 7.33), the probability limit of the product of two random variables equals the product of their probability limits, when the latter two exist. By doing this, the third and sixth terms of Eq. (17) cancel out due to Eq. (21), whereas the second term is computed using Eq. (18).

Interestingly, the large-sample approximation (25) has the form \(\frac{\sigma ^2}{T} K_i\), where

$$\begin{aligned} K_i:=\left( \frac{1+\rho }{1-\rho } + {\mathbb {E}} \left\{ \left\| A_N^{-\frac{1}{2}} \left( {\mathbb {E}} \left\{ {\underline{x}}_{i,1}\right\} -{\underline{x}}_i^{test}\right) \right\| _2^2\right\} \right) \end{aligned}$$
(26)

is a positive constant (possibly, a different constant for each unit i). This simplifies the analysis of the trade-off between training set size and precision of supervision performed in the next section, since one does not need to compute the exact expression of \(K_i\) to find the optimal trade-off.

In Appendix 3, an extension of the analysis made above is presented, by considering, respectively, the case of large N, and the one in which both N and T are large.

4 Optimal trade-off between training set size and precision of supervision for the fixed effects generalized least squares panel data model under the large-sample approximation

In this section, we are interested in optimizing the large-sample approximation (25) of the conditional generalization error when the variance \(\sigma ^2\) is modeled as a decreasing function of the supervision cost per example c, and there is an upper bound C on the total supervision cost NTc associated with the whole training set. In the analysis, N is fixed, and T is chosen as \(\left\lfloor \frac{C}{N c} \right\rfloor\). Moreover, the supervision cost per example c is allowed to take values on the interval \([c_{\mathrm{min}}, c_{\mathrm{max}}]\), where \(0< c_{\mathrm{min}} < c_{\mathrm{max}}\), so that the resulting T belongs to \(\left\{ \left\lfloor \frac{C}{N c_{\mathrm{max}}} \right\rfloor , \ldots , \left\lfloor \frac{C}{N c_{\mathrm{min}}} \right\rfloor \right\}\). In the following, C is supposed to be sufficiently large, so that the large-sample approximation (25) can be assumed to hold for every \(c \in [c_{\mathrm{min}}, c_{\mathrm{max}}]\).

Consistently with (Gnecco and Nutarelli 2019, 2019, 2020), we adopt the following model for the variance \(\sigma ^2\), as a function of the supervision cost per example c:

$$\begin{aligned} \sigma ^2(c)=k c^{-\alpha }\,, \end{aligned}$$
(27)

where \(k,\alpha > 0\). For \(0< \alpha < 1\), the precision of each supervision is characterized by “decreasing returns of scale” with respect to its cost because, if one doubles the supervision cost per example c, then the precision \(1/\sigma ^2(c)\) becomes less than two times its initial value (or equivalently, the variance \(\sigma ^2(c)\) becomes more than one half its initial value). Conversely, for \(\alpha > 1\), there are “increasing returns of scale” because, if one doubles the supervision cost per example c, then the precision \(1/\sigma ^2(c)\) becomes more than two times its initial value (or equivalently, the variance \(\sigma ^2(c)\) becomes less than one half its initial value). The case \(\alpha =1\) is intermediate and refers to “constant returns of scale”. In all the cases above, the precision of each supervision increases by increasing the supervision cost per example c. Finally, it is worth observing that, according to the model (3) for the covariance matrix of the vector of measurement noises, the correlation coefficient between successive measurement noises does not depend on c.

Concluding, under the assumptions above, the optimal trade-off between the training set size and the precision of supervision for the fixed effects generalized least squares panel data model is modeled by the following optimization problem:

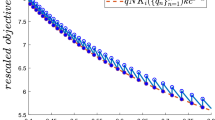
$$\begin{aligned} \underset{c \in [c_{\mathrm{min}}, c_{\mathrm{max}}]}{\mathrm{minimize}} \, K_i k \frac{c^{-\alpha }}{\left\lfloor \frac{C}{N c} \right\rfloor -1}\,. \end{aligned}$$
(28)

By a similar argument as in the proof of Gnecco and Nutarelli (2019, Proposition 3.2), when C is sufficiently large, the objective function \(C K_i k\frac{c^{-\alpha }}{\left\lfloor \frac{C}{N c} \right\rfloor -1}\) of the optimization problem (28), rescaled by the multiplicative factor C, can be approximated, with a negligible error in the maximum norm on \([c_{\mathrm{min}}, c_{\mathrm{max}}]\), by \(N K_i k c^{1-\alpha }\). In order to illustrate this issue, Fig. 1 shows the behavior of the rescaled objective functions \(C K_i k\frac{c^{-\alpha }}{\left\lfloor \frac{C}{N c} \right\rfloor -1}\) and \(N K_i k c^{1-\alpha }\) for the three cases \(0<\alpha = 0.5 < 1\), \(\alpha = 1.5 > 1\), and \(\alpha = 1\) (the values of the other parameters are \(k=0.5\), \(K_i=2\), \(N=10\), \(C={200}\), \(c_{\mathrm{min}}=0.4\), and \(c_{\mathrm{max}}=0.8\)). The additional approximation \({C N} K_i k\frac{c^{1-\alpha }}{C -N c}\) (which differs negligibly from \(N K_i k c^{1-\alpha }\) for large C) is also reported in the figure.

Concluding, under the approximation above, one can replace the optimization problem (28) with

$$\begin{aligned} \underset{c \in [c_{\mathrm{min}}, c_{\mathrm{max}}]}{\mathrm{minimize}} \, N K_i k c^{1-\alpha }\,, \end{aligned}$$
(29)

whose optimal solutions \(c^\circ\) have the following expressions:

  1. 1.

    if \(0< \alpha < 1\) (“decreasing returns of scale”): \(c^\circ = c_{\mathrm{min}}\);

  2. 2.

    if \(\alpha > 1\) (“increasing returns of scale”): \(c^\circ = c_{\mathrm{max}}\);

  3. 3.

    if \(\alpha = 1\) (“constant returns of scale”): \(c^\circ =\) any cost c in the interval \([c_{\mathrm{min}}, c_{\mathrm{max}}]\).

In summary, the results of the analysis show that, in the case of “decreasing returns of scale”, “many but bad” examples are associated with a smaller conditional generalization error than “few but good” ones. The opposite occurs for “increasing returns of scale”, whereas the case of “constant returns of scale” is intermediate. These results are qualitatively in line with the ones obtained in (Gnecco and Nutarelli 2019, 2019, 2020) for simpler linear regression problems, to which different regression algorithms were applied (respectively, ordinary least squares, weighted least squares, and fixed effects ordinary least squares). This depends on the fact that, in all these cases, the large-sample approximation of the conditional generalization error has the same functional form \(\frac{\sigma ^2}{T} K_i\) (although different positive constants \(K_i\) are involved in the various cases).

One can observe that, in order to discriminate among the three cases of the analysis reported above, one does not need to know the exact values of the constants \(\rho\), k, \(K_i\), and N. Moreover, to discriminate between the first two cases, it is not necessary to know the exact value of the positive constant \(\alpha\) (indeed, it suffices to know if \(\alpha\) belongs, respectively, to the interval (0, 1) or the one \((1,+\infty )\)). Interestingly, no precise knowledge of the probability distributions of the input examples (one for each unit) is needed. In particular, different probability distributions may be associated with different units, without affecting the results of the analysis. Finally, the same conclusions as above are reached if the objective function in (29) is replaced by the summation of the large-sample approximation of the conditional generalization error over all the N units. In that case, the constant \(K_i\) in (29) is replaced by \(K:=\sum _{i=1}^N K_i\).

Fig. 1
figure 1

Plots of the rescaled objective functions \(C K_i k\frac{c^{-\alpha }}{\left\lfloor \frac{C}{N c} \right\rfloor -1}\), \(C N K_i k c^{1-\alpha }\), \(C N K_i k\frac{c^{1-\alpha }}{C -N c}\), for \(\alpha = 0.5\) (a), \(\alpha = 1.5\) (b), and \(\alpha = 1\) (c). The values of the other parameters are reported in the text

Full size image

5 Numerical results

In this section, the theoretical results obtained in the paper are tested through simulations. For each c, the following empirical approximation of the summation of the generalization error over all the units, conditioned on the training input data, is adopted. It is based on \({\mathcal {N}}^{tr}\) training sets and \(N^{test}_i\) test examples for each unit i (\(i=1,\ldots ,N\)), hence on a total number \(N^{test}=\sum _{i=1}^N N^{test}_i\) of test examples:

$$\begin{aligned}&\sum _{i=1}^N {\mathbb {E}} \left\{ \left( \hat{\eta }_{i,FEGLS}+\underline{\hat{\beta }}_{FEGLS}'{\underline{x}}_i^{test}-\eta _i-\underline{\beta }'{\underline{x}}_i^{test}\right) ^2 \big | \{{\underline{x}}_{n,t}\}_{n=1,\ldots ,N}^{t=1,\ldots ,T}\right\} \nonumber \\&\quad \simeq \frac{1}{N^{test}} \sum _{i=1}^N \sum _{h=1}^{N^{test}_i} \frac{1}{{\mathcal {N}}^{tr}} \sum _{j=1}^{{\mathcal {N}}^{tr}} \bigg (\hat{\eta }_{i,FEGLS}^{j}+\left( \underline{\hat{\beta }}_{FEGLS}^{j}\right) '{\underline{x}}_{i,h}^{test}-\eta _i-\underline{\beta }'{\underline{x}}_{i,h}^{test}\bigg )^2\,. \end{aligned}$$
(30)

In Eq. (30), \(({\underline{x}}^{test}_{i,h}, y^{test}_{i,h})\) is the h-th generated test example for the unit i, and \(\underline{\hat{\beta }}_{FEGLS}^j\) is the estimate of the vector \(\underline{\beta }\) obtained using the j-th generated training set. Similarly, \(\hat{\eta }_{i,FEGLS}^{j}\) is the estimate of the individual constant \(\eta _i\) obtained using the j-th generated training set. For each choice of c, all the \({\mathcal {N}}^{tr}\) generated training sets share the same training input data matrices \(X_n\), but differ in the random choice of the measurement noise. The number of rows in each matrix \(X_n\) is increased when c is reduced from \(c_{\mathrm{max}}\) to \(c_{\mathrm{min}}\), by increasing the number of observations T. For a fair comparison, when doing this, the rows already present in each matrix \(X_n\) are kept fixed. Finally, the same test examples (generated independently from the training sets) are used to assess the performance of the fixed effects generalized least squares estimates for different costs per example c.

For the simulations, we choose \(N=20\) for the number of units, \(p = 5\) for the number of features, \(c_{\mathrm{min}} = 2\), \(c_{\mathrm{max}}=4\), \({\mathcal {N}}^{tr} = 100\) for the number of training sets, \(N^{test}_i=50\) for the number of test examples per unit (hence the total number of test examples is \(N^{test}=1000\)). The number of training examples per unit is \(T = 50\) for \(c=c_{\mathrm{min}}\), and \(T = 25\) for \(c=c_{\mathrm{max}}\). In this way, the (upper bound on the) total supervision cost is \(C = 2000\) for both cases. Without loss of generality, the constant k in the model (27) of the variance of the supervision cost is assumed to be equal to 1. The components of the parameter vector \(\underline{\beta }\) are generated randomly and independently according to a uniform distribution on \([-1, 1]\), obtaining

$$\begin{aligned} \underline{\beta } = [-0.8562,0.6837,0.2640,-0.0038,-0.0598]'\,. \end{aligned}$$
(31)

Similarly, the fixed effects \(\eta _n\) (for \(n=1,\ldots ,N\)) are generated randomly and independently according to a uniform distribution on \([-1, 1]\), obtaining the vector

$$\begin{aligned} \underline{\eta }= & {} \bigg [-0.2330,-0.2779,-0.0434,-0.9707,0.6848,0.0720,-0.2033,-0.6877,0.5967,-0.7895, \nonumber \\&\,\,\,\,\,\,0.6500,0.9717,0.9673,-0.1443,-0.4211,0.3109,0.5189,0.4709,0.4414,-0.8382\bigg ]' \in {\mathbb {R}}^N\,. \end{aligned}$$
(32)

For both training and test sets, the input data associated with each unit are generated as realizations of a multivariate Gaussian distribution with mean \({\underline{0}}\) and covariance matrix

$$\begin{aligned} {\mathrm{Var}}\left( {\underline{x}}_{n,t}\right) ={\mathrm{Var}}\left( {\underline{x}}_i^{test}\right) ={\begin{bmatrix} 1.4016 &{} 0.8086 &{} 1.2594 &{} 0.9866 &{} 0.6206 \\ 0.8086 &{} 0.9988 &{} 0.9518 &{} 1.2044 &{} 0.5003 \\ 1.2594 &{} 0.9518 &{} 1.9087 &{} 1.5945 &{} 0.7120 \\ 0.9866 &{} 1.2044 &{} 1.5945 &{} 1.9089 &{} 0.8294 \\ 0.6206 &{} 0.5003 &{} 0.7120 &{} 0.8294 &{} 0.4776 \end{bmatrix}}\,, \end{aligned}$$
(33)

which is symmetric and positive definite. This covariance matrix has been generated by setting \({\mathrm{Var}}\left( {\underline{x}}_{n,t}\right) ={\mathrm{Var}}\left( {\underline{x}}_i^{test}\right) ={A_x A_x'}\), where the elements of \({A_x} \in {\mathbb {R}}^{p \times p}\) have been randomly and independently generated according to a uniform probability density on the interval [0,1]. The parameter \(\rho\) in the covariance matrix (3) of the zero-mean vector of measurement noises (modeled in the simulations by a multivariate Gaussian distribution) is chosen to be equal to 0.3. As a robustness check, the whole procedure is repeated 100 times.

The results of the analysis are displayed in Tables 1 (for \(\alpha = 0.5\)), 2 (for \(\alpha = 1.5\)), and 3 (for \(\alpha = 1\)). Each table reports the results obtained in each repetition for \(c=c_{\mathrm{min}}\) and \(c=c_{\mathrm{max}}\). The total simulation time (for a MATLAB 9.4 implementation of the procedure) is of about 501 sec on a notebook with a 2.30 GHz Intel(R) Core(TM) i5-4200U CPU and 6 GB of RAM. A statistical analysis of the elements of the tables leads to the following conclusions:

  1. 1.

    for \(\alpha =0.5\) (Table 1), the application of a one-sided Wilcoxon matched-pairs signed-rank test (Barlow 1989, Sect. 9.2.3) rejects the null hypothesis that the difference between the approximated performance index from Eq. (30) for \(c=c_{\mathrm{max}}\) and the one for \(c=c_{\mathrm{min}}\) has a symmetric distribution around its median and that median is smaller than or equal to 0 (p-value=\({1.9780 \cdot 10^{-18}}\), significance level set to 0.05);

  2. 2.

    for \(\alpha =1.5\) (Table 2), the application of a one-sided Wilcoxon matched-pairs signed-rank test rejects the null hypothesis that the same difference as above has a symmetric distribution around its median and that median is larger than or equal to 0 (p-value=\({1.9780 \cdot 10^{-18}}\), significance level set to 0.05);

  3. 3.

    for \(\alpha =1\) (Table 3), the application of a two-sided Wilcoxon matched-pairs signed-rank test fails to reject the null hypothesis that the same difference as above has a symmetric distribution around its median and that median is equal to 0 (p-value=0.4453, significance level set to 0.05).

Concluding, the tables show that the simulation results are in perfect agreement with the theoretical ones, leading to the same conclusions. Interestingly, this holds even though relatively small values for T have been chosen for the simulations.

Table 1 For \(\alpha =0.5\): values of the approximated performance index from Eq. (30) for the 100 repetitions of the simulation procedure
Full size table
Table 2 For \(\alpha =1.5\): values of the approximated performance index from Eq. (30) for the 100 repetitions of the simulation procedure
Full size table
Table 3 For \(\alpha =1\): values of the approximated performance index from Eq. (30) for the 100 repetitions of the simulation procedure
Full size table

6 Discussion and possible extensions

Up to the authors’ knowledge, the analysis and the optimization, made in the present article, of the conditional generalization error in regression as a trade-off between training set size and precision of supervision, has been carried out only rarely in the literature. In particular, the authors believe that it was never addressed for the fixed effects generalized least squares panel data model. Nevertheless, the methodology used in the present article is similar to the one exploited in the context of the optimization of sample survey design, in which some parameters of the design are optimized to minimize, e.g., the sampling variance (see, for instance, the classical solution provided by Neyman allocation for optimal stratified sampling design, in case the dataset has a fixed size (Groves et al. 2004). It also shares some similarity to the approach used in Nguyen et al. (2009) - in a context, however, in which linear regression is marginally involved, since only arithmetic averages of measurement results are considered - for the optimal design of measurement devices. Finally, the present article can also be related to some recent works which, according to an emerging trend in the literature, combine methods from machine learning, optimization, and econometrics (Athey and Imbens 2016; Bargagli Stoffi and Gnecco 2018, 2020; Varian 2014) (e.g., the generalization error - which is typically considered in machine learning, and optimized by solving suitable optimization problems - is not investigated in the classical analysis of the fixed effects generalized least squares panel data model (Wooldridge 2002, Chapter 10)). In this way, the interaction between machine learning and optimization—which appears commonly in the literature (Bennett and Parrado-Hernández 2006; Bianchini et al. 1998; Gnecco et al. 2013; Gori 2017; Özöğür-Akyüz et al. 2011; Sra et al. 2011)—is extended to the econometrics field.

For what concerns practical applications, the theoretical results obtained in the analysis made in this work could be applied to the acquisition design of fixed effects panel data in both microeconometrics and macroeconometrics (Greene 2003, Chapter 13). A semi-artificial validation on existing datasets could also be performed by inserting artificial noise with variance expressed as in Eq. (27), possibly with the inclusion of an additional constant term in that variance, to model the case of the original dataset before the insertion of the artificial noise. As a possible extension, one could investigate and optimize the trade-off between training set size and precision of supervision for the unbalanced FEGLS case (in which different units are associated with possibly different numbers of observations)Footnote 5, for the situation in which some parameters of the noise model have to be estimated either from the data or from a subset of the data, and for the case of a non-zero correlation of measurement errors for the observations associated with different units. Such developments could open the way to the application of the proposed framework to real-world problems, e.g., in econometrics. Another possible extension concerns the replacement in the investigation of the fixed effects panel data model with the random effects one (Greene 2003, Chapter 13), which is also commonly applied to deal with the analysis of economic data, and differs from the fixed effects panel data model in that its parameters are random variablesFootnote 6. In the present analysis, however, a possible advantage of the fixed effects panel data model is that it also makes it possible to get estimates of the individual constants \(\eta _n\) (see Eq. (12)), which appear in the expression (16) of the conditional generalization error. Finally, another possible extension involves the case of dynamic panel data models (Cameron and Trivedi 2005, Chapter 21).