1 Introduction

Feature learning is a crucial component in many applications of machine learning. New feature extraction methods or data representations are often responsible for breakthroughs in performance, as illustrated by the kernel trick in support vector machines (Schölkopf and Smola 2002) and their feature learning counterpart in multiple kernel learning (Bach et al. 2004), and more recently by deep architectures (Bengio 2009).

Among all the feature extraction approaches, one major family of dimensionality reduction methods (Van Der Maaten et al. 2009; Burges 2010) consists in estimating a linear subspace of the data. Although very simple, linear subspaces have many advantages. They are easy to interpret, and can be inverted, at least in a lest-squares way. This latter property has been used for instance in PCA denoising (Zhang et al. 2010). Linear projection is also a key component in random projection methods (Fern and Brodley 2003) or compressed sensing and is often used as a first pre-processing step, such as the linear part in a neural network layer. Finally, linear projections only imply matrix products and stream therefore particularly well on any type of hardware (CPU, GPU, DSP).

Linear dimensionality reduction techniques come in all flavors. Some of them, such as PCA, are inherently unsupervised; some can consider labeled data and fall in the supervised category. We consider in this paper linear and supervised techniques. Within that category, two families of methods stand out: Given a dataset of pairs of vectors and labels \(\{(\mathbf {x}_i,y_i)\}_i\), with \(\mathbf {x}_i \in \mathbb {R}^d\), the goal of Fisher Discriminant Analysis (FDA) and variants is to learn a linear map \(\mathbf {P}:\mathbb {R}^d \rightarrow \mathbb {R}^p\), \(p\ll d\), such that the embeddings of these points \(\mathbf {P}\mathbf {x}_i\) can be easily discriminated using linear classifiers. Mahalanobis metric learning (MML) follows the same approach, except that the quality of the embedding \(\mathbf {P}\) is judged by the ability of a k-nearest neighbor algorithm (not a linear classifier) to obtain good classification accuracy.

1.1 FDA and MML, in both global and local flavors

FDA attempts to maximize w.r.t. \(\mathbf {P}\) the sum of all distances \(\Vert \mathbf {P}\mathbf {x}_i-\mathbf {P}\mathbf {x}_{j'} \Vert \) between pairs of samples from different classes \(c,c'\) while minimizing the sum of all distances \(\Vert \mathbf {P}\mathbf {x}_i-\mathbf {P}\mathbf {x}_j \Vert \) between pairs of samples within the same class c (Friedman et al. 2001, §4.3). Because of this, it is well documented that the performance of FDA degrades when class distributions are multimodal. Several variants have been proposed to tackle this problem (Friedman et al. 2001, §12.4). For instance, a localized version of FDA was proposed by Sugiyama (2007), which boils down to discarding the computation for all pairs of points that are not neighbors.

On the other hand, the first techniques that were proposed to learn metrics (Xing et al. 2003) used a global criterion, namely a sum on all pairs of points. Later on, variations that focused instead exclusively on local interactions, such as LMNN (Weinberger and Saul 2009), were shown to be far more efficient in practice. Supervised dimensionality approaches stemming from FDA or MML consider thus either global or local interactions between points, namely, either all differences \(\Vert \mathbf {P}\mathbf {x}_i-\mathbf {P}\mathbf {x}_j \Vert \) have an equal footing in the criterion they optimize, or, on the contrary, \(\Vert \mathbf {P}\mathbf {x}_i-\mathbf {P}\mathbf {x}_j \Vert \) is only considered for points such that \(\mathbf {x}_i\) is close to \(\mathbf {x}_j\).

Fig. 1
figure 1

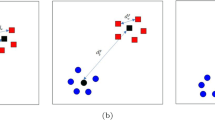
Weights used for inter/intra class variances for FDA, Local FDA and WDA for different regularizations \(\lambda \). Only weights for two samples from class 1 are shown. The color of the link darkens as the weight grows. FDA computes a global variance with uniform weight on all pairwise distances, whereas LFDA focuses only on samples that lie close to each other. WDA relies on an optimal transport matrix \(\mathbf {T}\) that matches all points in one class to all other points in another class (most links are not visible because they are colored in white as related weights are too small). WDA has both a global (due to matching constraints) and local (due to transportation cost minimization) outlook on the problem, with a tradeoff controlled by the regularization strength \(\lambda \)

Full size image

1.2 WDA: global and local

We introduce in this work a novel approach that incorporates both a global and local perspective. WDA can achieve this blend through the mathematics of optimal transport ( see for instance the recent book of Peyré and Cuturi (2018) for an introduction and exposition of some of the computational we will use in this paper). Optimal transport provides a powerful toolbox to compute distances between two empirical probability distributions. Optimal transport does so by considering all probabilistic couplings between these two measures, to select one, denoted T, that is optimal for a given criterion. This coupling now describes interactions at both a global and local scale, as reflected by the transportation weight \(T_{ij}\) that quantifies how important the distance \(\Vert \mathbf {P}\mathbf {x}_i-\mathbf {P}\mathbf {x}_{j} \Vert \) should be to obtain a good projection matrix \(\mathbf {P}\). Indeed, such weights are decided by (i) making sure that all points in one class are matched to all points in the other class (global constraint, derived through marginal constraints over the coupling); (ii) making sure that points in one class are matched only to few similar points of the other class (local constraint, thanks to the optimality of the coupling, that is a function of local costs). Our method has the added flexibility that it can interpolate, through a regularization parameter, between an exclusively global viewpoint (identical, in that case, to FDA), to a more local viewpoint with a global matching constraint (different, in that sense, to that of purely local tools such as LMNN or Local-FDA). In mathematical terms, we adopt the ratio formulation of FDA to maximize the ratio of the regularized Wasserstein distances between inter class populations and between the intra-class population with itself, when these points are considered in their projected space:

$$\begin{aligned} \max _{\mathbf {P}\in \varDelta }\quad \frac{\sum _{c,c'> c}W_\lambda (\mathbf {P}\mathbf {X}^{c},\mathbf {P}\mathbf {X}^{c'})}{\sum _{c}W_\lambda (\mathbf {P}\mathbf {X}^{c},\mathbf {P}\mathbf {X}^{c})} \end{aligned}$$
(1)

where \(\varDelta =\{ \mathbf {P}=[\mathbf {p_1},\dots ,\mathbf {p}_p] \quad |\quad \mathbf {p}_i \in \mathbb {R}^d, \Vert \mathbf {p}_i\Vert _2=1 \quad \text { and }\mathbf {p}_i^\top \mathbf {p}_j=0\text { for } i\ne j \}\) is the Stiefel manifold (Absil et al. 2009), the set of orthogonal \(d\times p\) matrices; \(\mathbf {P}\mathbf {X}^{c}\) is the matrix of projected samples from class c. \(W_\lambda \) is the regularized Wasserstein distance proposed by Cuturi (2013), which can be expressed as \(W_\lambda (\mathbf {X},\mathbf {Z})=\sum _{i,j}T^\star _{i,j}\Vert \mathbf {x}_i-\mathbf {z}_j\Vert ^2_2\), \(T^\star _{i,j}\) being the coordinates of the entropic-regularized Optimal Transport (OT) matrix \(\mathbf {T}^\star \) (see Sect. 2). These entropic-regularized Wasserstein distances measure the dissimilarity between empirical distributions by considering pairwise distances between samples. The strength of the regularization \(\lambda \) controls the local information involved in the distance computation. Further analyses and intuitions on the role on the within-class distances in the optimization problem are given in the Sect. 4.

When \(\lambda \) is small, we will show that WDA boils down to FDA. When \(\lambda \) is large, WDA tries to split apart distributions of classes by maximizing their optimal transport distance. In that process, for a given example \(\mathbf {x}_i\) in one class, only few components \(T_{i,j}\) will be activated so that \(\mathbf {x}_i\) will be paired with few examples. Figure 1 illustrates how pairing weights \(T_{i,j}\) are defined when comparing Wasserstein discriminant analysis (WDA, with different regularization strengths) with FDA (purely global), and Local-FDA (purely local) (Sugiyama 2007). Another strong feature brought by regularized Wasserstein distances is that relations between samples (as given by the optimal transport matrix \(\mathbf {T}\)) are estimated in the projected space. This is an important difference compared to all previous local approaches which estimate local relations in the original space and make the hypothesis that these relations are unchanged after projection.

1.3 Paper outline

Section 2 provides background on regularized Wasserstein distances. The WDA criterion and its practical optimization is presented in Sect. 3. Section 4 by discusses properties of WDA and related works. Numerical experiments are provided in Sect. 5. Section 6 concludes the paper and introduces perspectives.

2 Background on Wasserstein distances

Wasserstein distances, also known as earth mover distances, define a geometry over the space of probability measures using principles from optimal transport theory (Villani 2008). Recent computational advances (Cuturi 2013; Benamou et al. 2015) have made them scalable to dimensions relevant to machine learning applications.

2.1 Notations and definitions

Let \(\mu =\frac{1}{n}\sum _{i} \delta _{\mathbf {x}_i}\), \(\nu =\frac{1}{m}\sum _{i} \delta _{\mathbf {z}_i}\) be two empirical measures with locations in \(\mathbb {R}^d\) stored in matrices \(\mathbf {X}=[\mathbf {x}_1,\ldots ,\mathbf {x}_n]\) and \(\mathbf {Z}=[\mathbf {z}_1,\ldots ,\mathbf {z}_m]\). The pairwise squared Euclidean distance matrix between samples in \(\mu \) and \(\nu \) is defined as \(\mathbf {M}_{\mathbf {X},\mathbf {Z}}:= [\Vert \mathbf {x}_i-\mathbf {z}_j \Vert _2^2]_{ij} \in \mathbb {R}^{n\times m}.\) Let \(U_{nm}\) be the polytope of \(n\times m\) nonnegative matrices such that their row and column marginals are equal to \(\mathbf {1}_n/n\) and \(\mathbf {1}_m/m\) respectively. Writing \({\mathbf {1}}_n\) for the n-dimensional vector of ones, we have:

$$\begin{aligned} U_{nm}:= \{ \mathbf {T}\in \mathbb {R}_+^{n\times m}\;:\; \mathbf {T}\mathbf {1}_m = \mathbf {1}_n/n,\, \mathbf {T}^T \mathbf {1}_n = \mathbf {1}_m/m \}. \end{aligned}$$

2.2 Regularized Wassersein distance

Let \(\langle \mathbf {A} , \mathbf {B}\,\rangle := {{\mathrm{tr}}}(\mathbf {A}^T \mathbf {B})\) be the Frobenius dot-product of matrices. For \(\lambda \ge 0\), the regularized Wasserstein distance we adopt in this paper between \(\mu \) and \(\nu \) is (and with a slight abuse of notation):

$$\begin{aligned} W_\lambda (\mu ,\nu ) :=W_\lambda (\mathbf {X},\mathbf {Z}) :=\langle \mathbf {T}_\lambda , \mathbf {M}_{\mathbf {X},\mathbf {Z}}\,\rangle , \end{aligned}$$
(2)

where \(\mathbf {T}_\lambda \) is the solution of an entropy-smoothed optimal transport problem,

$$\begin{aligned} \mathbf {T}_\lambda :={{\mathrm{argmin}}}_{\mathbf {T}\in U_{nm}}\,\lambda \langle \mathbf {T} , \mathbf {M}_{\mathbf {X},\mathbf {Z}}\,\rangle -\varOmega (\mathbf {T}), \end{aligned}$$
(3)

where \(\varOmega (\mathbf {T})\) is the entropy of \(\mathbf {T}\) seen as a discrete joint probability distribution, namely \(\varOmega (\mathbf {T}):=-\sum _{ij}t_{ij} \log (t_{ij}).\) Note that problem (3) can be solved very efficiently using Sinkhorn’s fixed-point iterations (Cuturi 2013). The solution of the optimization problem can be expressed as:

$$\begin{aligned} { \mathbf {T}={{\mathrm{diag}}}(\mathbf {u}) \mathbf {K}{{\mathrm{diag}}}(\mathbf {v}) =\mathbf {u}{\mathbf {1}}_m^T \circ \mathbf {K}\circ {\mathbf {1}}_n {\mathbf {v}}^T, } \end{aligned}$$
(4)

where \(\circ \) stands for elementwise multiplication and \(\mathbf {K}\) is the matrix whose elements are \(K_{i,j} = e^{-\lambda M_{i,j}}\). The Sinkhorn iterations consist in updating left/right scaling vectors \(\mathbf {u}^k\) and \(\mathbf {v}^k\) of the matrix \(\mathbf {K}=e^{-\lambda \mathbf {M}}\). These updates take the following form for iteration k:

$$\begin{aligned} \mathbf {v}^k=\frac{{\mathbf {1}}_m/m}{{\mathbf {K}}^T\mathbf {u}^{k-1}}, \quad \mathbf {u}^k=\frac{{\mathbf {1}}_n/n}{\mathbf {K}\mathbf {v}^k} \end{aligned}$$
(5)

with an initialization which will be fixed to \(\mathbf {u}^0={\mathbf {1}}_n\). Because it only involves matrix products, the Sinkhorn algorithm can be streamed efficiently on parallel architectures such as GPGPUs.

3 Wasserstein discriminant analysis

In this section we discuss optimization problem (1) and propose an efficient approach to compute the gradient of its objective.

3.1 Optimization problem

To simplify notations, let us define a separate empirical measure for each of the C classes: samples of class c are stored in matrices \(\mathbf {X}^c\); the number of samples from class c is \(n_c\). Using the definition (2) of regularized Wasserstein distance, we can write the Wasserstein Discriminant Analysis optimization problem as

$$\begin{aligned}&\max _{\mathbf {P}\in \varDelta } \quad \left\{ J(\mathbf {P},\mathbf {T}(\mathbf {P}))=\frac{\sum _{c,c'> c} \langle \mathbf {P}^T\mathbf {P} , \mathbf {C}^{c,c'}\,\rangle }{\sum _{c} \langle \mathbf {P}^T\mathbf {P} , \mathbf {C}^{c,c}\,\rangle }\right\} \\&\text {s.t. } \mathbf {C}^{c,c'}=\sum _{i,j}T^{c,c'}_{i,j}( \mathbf {x}^c_i-\mathbf {x}^{c'}_j)( \mathbf {x}^c_i-\mathbf {x}^{c'}_j)^T,\quad \forall c,c'\nonumber \\&\text {and } \mathbf {T}^{c,c'}=\small {{\mathrm{argmin}}}_{\mathbf {T}\in U_{n_cn_{c'}}}\,\lambda \langle \mathbf {T} , \mathbf {M}_{\mathbf {P}\mathbf {X}^{c},\mathbf {P}\mathbf {X}^{c'}}\,\rangle -\varOmega (\mathbf {T}),\nonumber \end{aligned}$$
(6)

which can be reformulated as the following bilevel problem

$$\begin{aligned}&\max _{\mathbf {P}\in \varDelta } \quad \quad J(\mathbf {P},\mathbf {T}(\mathbf {P})) \end{aligned}$$
(7)
$$\begin{aligned}&\text {s.t. } \mathbf {T}(\mathbf {P})={{\mathrm{argmin}}}_{\mathbf {T}\in U_{n_cn_{c'}}}\quad E(\mathbf {T},\mathbf {P}) \end{aligned}$$
(8)

where \(\mathbf {T}=\{\mathbf {T}^{c,c'}\}_{c,c'}\) contains all the transport matrices between classes and the inner problem function E is defined as

$$\begin{aligned} E(\mathbf {T}, \mathbf {P})=\sum _{c,c>=c'} \lambda \langle \mathbf {T}^{c,c'} , \mathbf {M}_{\mathbf {P}\mathbf {X}^{c},\mathbf {P}\mathbf {X}^{c'}}\,\rangle -\varOmega (\mathbf {T}^{c,c'}). \end{aligned}$$
(9)

The objective function J can be expressed as

$$\begin{aligned} J(\mathbf {P},\mathbf {T}(\mathbf {P}))= \frac{ \langle \mathbf {P}^T\mathbf {P} , \mathbf {C}_{b}\,\rangle }{ \langle \mathbf {P}^T\mathbf {P} , \mathbf {C}_{w}\,\rangle } \end{aligned}$$

where \(\mathbf {C}_b=\sum _{c,c'> c}\mathbf {C}_{c,c'}\) and \(\mathbf {C}_w=\sum _{c} \mathbf {C}_{c,c}\) are the between and within cross-covariance matrices that depend on \(\mathbf {T}(\mathbf {P})\). Optimization problem (7)-(8) is a bilevel optimization problem, which can be solved using gradient descent (Colson et al. 2007). Indeed, J is differentiable with respect to \(\mathbf {P}\). This comes from the fact that optimization problems in Eq. (8) are all strictly convex, making solutions of the problems unique, hence \(\mathbf {T}(\mathbf {P})\) is smooth and differentiable (Bonnans and Shapiro 1998).

Thus, one can compute the gradient of J directly w.r.t. \(\mathbf {P}\) using the chain rule as follows

$$\begin{aligned} \nabla _\mathbf {P}J(\mathbf {P},\mathbf {T}(\mathbf {P}))=\frac{\partial J(\mathbf {P},\mathbf {T})}{\partial \mathbf {P}} +\sum _{c,c'\ge c} \frac{\partial J(\mathbf {P},\mathbf {T})}{\partial \mathbf {T}^{c,c'}} \frac{\partial \mathbf {T}^{c,c'}}{\partial \mathbf {P}} \end{aligned}$$
(10)

The first term in gradient (10) suppose that \(\mathbf {T}\) is constant and can be computed [Eq. 94–95 (Petersen et al. 2008)] as

$$\begin{aligned} \frac{\partial J(\mathbf {P},\mathbf {T})}{\partial \mathbf {P}}=\mathbf {P}\left( \frac{2}{\sigma _w^2}\mathbf {C}_{b}-\frac{2\sigma _b^2}{\sigma _w^4}\mathbf {C}_{w}\right) \end{aligned}$$
(11)

with \(\sigma _w^2=\langle \mathbf {P}^T\mathbf {P} , \mathbf {C}_{w}\,\rangle \) and \(\sigma _b^2=\langle \mathbf {P}^T\mathbf {P} , \mathbf {C}_{b}\,\rangle \). In order to compute the second term in (10), we will separate the cases when \(c=c'\) and \(c\ne c'\) as it corresponds to their position in the fraction of Eq. (6). Their partial derivative is obtained directly from the scalar product and is a weighted vectorization of the transport cost matrix

$$\begin{aligned} \frac{\partial J(\mathbf {P},\mathbf {T})}{\partial \mathbf {T}^{c,c'\ne c}}=\text {vec} \Big (\frac{1}{{\sigma _w^2}}\mathbf {M}_{\mathbf {P}\mathbf {X}^{c},\mathbf {P}\mathbf {X}^{c'}}\Big ) \quad \text {and} \quad \frac{\partial J(\mathbf {P},\mathbf {T})}{\partial \mathbf {T}^{c,c}}=-\text {vec}\Big ({\frac{\sigma _b^2}{\sigma _w^4}}\mathbf {M}_{\mathbf {P}\mathbf {X}^{c},\mathbf {P}\mathbf {X}^{c}}\Big ). \end{aligned}$$
(12)

We will see in the remaining that the main difficulty stands in computing the Jacobian \( {\partial \mathbf {T}^{c,c'}}/{\partial \mathbf {P}}\) since the optimal transport matrix is not available as a closed form. We solve this problem using instead an automatic differentiation approach wrapped around the Sinkhorn fixed point iteration algorithm.

3.2 Automatic differentiation

A possible way to compute the Jacobian \(\partial \mathbf {T}^{c,c'}/\partial \mathbf {P}\) is to use the implicit function theorem as in hyperparameter estimation in ML (Bengio 2000; Chapelle et al. 2002). We detail that approach in the appendix but it requires inverting a very large matrix, and does not scale in practice. It also assumes that the exact optimal transport \(\mathbf {T}_\lambda \) is obtained at each iteration, which is clearly an approximation since we only have the computational budget for a finite, and usually small, number of Sinkhorn iterations.

Following the gist of Bonneel et al. (2016), which do not differentiate Sinkhorn iterations but a more complex fixed point iteration designed to compute Wasserstein barycenters, we propose in this section to differentiate the transportation matrices obtained after running exactly L Sinkhorn iterations, with a predefined L. Writing \(\mathbf {T}^k(\mathbf {P})\), for the solution obtained after k iterations as a function of \(\mathbf {P}\) for a given \(c,c'\) pair,

$$\begin{aligned} \mathbf {T}^k(\mathbf {P}) = {{\mathrm{diag}}}(\mathbf {u}^k)e^{-\lambda \mathbf {M}}{{\mathrm{diag}}}(\mathbf {v}^k) \end{aligned}$$

where \(\mathbf {M}\) is the distance matrix induced by \(\mathbf {P}\). \(\mathbf {T}^L(\mathbf {P})\) can then be directly differentiated:

$$\begin{aligned} \frac{\partial \mathbf {T}^k}{\partial \mathbf {P}}&= \frac{\partial [\mathbf {u}^k{\mathbf {1}}_m^T]}{\partial \mathbf {P}} \circ e^{-\lambda \mathbf {M}}\circ {\mathbf {1}}_n {\mathbf {v}^k}^T \nonumber \\&\quad +\,\mathbf {u}^k{\mathbf {1}}_m^T \circ \frac{\partial e^{-\lambda \mathbf {M}}}{\partial \mathbf {P}}\circ {\mathbf {1}}_n {\mathbf {v}^k}^T + \mathbf {u}^k{\mathbf {1}}_m^T \circ e^{-\lambda \mathbf {M}}\circ \frac{\partial { [{\mathbf {1}}_n\mathbf {v}^k}^T]}{\partial \mathbf {P}} \end{aligned}$$
(13)

Note that the recursion occurs as \(\mathbf {u}^k\) depends on \(\mathbf {v}^k\) whose is also related to \(\mathbf {u}^{k-1}\). The Jacobians that we need can then be obtained from Eq. (5). For instance, the gradient of one component of \(\mathbf {u}^k{\mathbf {1}}_m^T\) at the j-th line is

$$\begin{aligned} \frac{\partial \mathbf {u}^k_j}{\partial \mathbf {P}}= -\frac{1/n}{[\mathbf {K}\mathbf {v}^k]_j^2}\Big (\sum _i \frac{\partial \mathbf {K}_{j,i}}{ \partial \mathbf {P}}\mathbf {v}_i^k + \sum _i \mathbf {K}_{j,i} \frac{\partial \mathbf {v}_i^k}{ \partial \mathbf {P}} \Big ), \end{aligned}$$
(14)

while for \(\mathbf {v}^k\), we have

$$\begin{aligned} \frac{\partial \mathbf {v}^k_j}{\partial \mathbf {P}}= -\frac{1/m}{[\mathbf {K}^T \mathbf {u}^{k-1}]_j^2}\Big (\sum _i \frac{\partial \mathbf {K}_{i,j}}{ \partial \mathbf {P}}\mathbf {u}_{i}^{k-1} + \sum _i \mathbf {K}_{i,j} \frac{\partial \mathbf {u}_i^{k-1}}{ \partial \mathbf {P}} \Big ), \end{aligned}$$
(15)

and finally

$$\begin{aligned} \frac{\partial \mathbf {K}_{i,j}}{\partial \mathbf {P}}= - 2K_{i,j} \mathbf {P}(\mathbf {x}_i - \mathbf {x}_j^\prime ) (\mathbf {x}_i - \mathbf {x}_j^\prime )^T. \end{aligned}$$

The Jacobian \(\frac{\partial \mathbf {T}^k}{\partial \mathbf {P}}\) can be thus obtained by keeping track of all the Jacobians at each iteration and then by successively applying those equations. This approach is far cheaper than the implicit function theorem approach. Indeed, in this case, the computation of \(\frac{\partial \mathbf {T}}{\partial \mathbf {P}}\) is dominated by the complexity of computing \(\frac{\partial \mathbf {K}}{\partial \mathbf {P}}\) whose costs for one iteration is \(O(pn^2d^2)\) for \(n=m\). The complexity is then linear in L and quadratic in n.

3.3 Algorithm

In the above subsections, we have reformulated the WDA optimization problem so as to make it tractable. We have derived closed-form expressions of some elements of the gradient as well as an automatic differentiation strategy for computing gradients of the transport plans \(\mathbf {T}^{c,c^\prime }\) with respects to \(\mathbf {P}\).

Now that all these partial derivatives are computed, we can compute the gradient \(\mathbf {G}^k = \nabla _\mathbf {P}J(\mathbf {P}^k, \mathbf {T}(\mathbf {P}^k))\) at iteration k and apply classical manifold optimization tools such as projected gradient of Schmidt (2008) or a trust region algorithm as implemented in Manopt/Pymanopt (Boumal et al. 2014; Koep and Weichwald 2016). The latter toolbox includes tools to optimize over the Stiefel manifold, notably automatic conversions from Euclidean to Riemannian gradients. Algorithm 1 provide the steps of a projected gradient approach for solving WDA. We noted in there that at each iteration, we need to compute all the transport plans \(\mathbf {T}^{c,c^\prime }\), which are needed for computing \(\mathbf {C}_b\) and \(\mathbf {C}_w\). Automatic differentiation in the last steps of Algorithm 2 takes advantage of these transport plan computations for calculating and storing partial derivatives needed for Eq. 13.

figure a

From a computational complexity point of view, for each projected gradient iteration, we have the following complexity, considering that all classes are composed of n samples. For one iteration of the Sinkhorn–Knopp algorithm given in Algorithm 2, \(\mathbf {u}^k\) and \(\mathbf {v}^k\) are of complexity \(\mathcal {O}(n^2)\) while \(\{\frac{\partial \mathbf {v}_{j}^k}{ \partial \mathbf {P}}\}_j\) and \(\{\frac{\partial \mathbf {u}_{j}^k}{ \partial \mathbf {P}}\}_n\) are both \(\mathcal {O}(n^2dp)\). In this algorithm, complexity is dominated by the one of \(\frac{\partial \mathbf {K}_{i,j}}{ \partial \mathbf {P}}\) which costs is \(\mathcal {O}(n^2d^2p)\), although it is computed only once. In Algorithm 1, the costs of \(\mathbf {C}_b\) and \(\mathbf {C}_w\) are \(\mathcal {O}(n^2d^2)\) and Eqs. (11) and (12) yields respectively a complexity of \(\mathcal {O}(pd^2)\) and \(\mathcal {O}(n^2d^2p)\). Note that the cost of computing \(\frac{\partial \mathbf {T}^k}{\partial \mathbf {P}}\) is dominated by those of \(\{\frac{\partial \mathbf {v}_{j}^k}{ \partial \mathbf {P}}\}_j\) and \(\{\frac{\partial \mathbf {u}_{j}^k}{ \partial \mathbf {P}}\}_n\). Finally, the cost computing the sum in \(\mathbf {G}^k = \nabla _\mathbf {P}J(\mathbf {P}^k, \mathbf {T}(\mathbf {P}^k)\) achieves a global complexity of \(\mathcal {O}(C^2n^2dp)\). In conclusion, our algorithm is quadratic in both the number of samples in the classes and in the original dimension of the problem.

figure b

4 Discussions

4.1 Wasserstein discriminant analysis: local and global

As we have stated, WDA allows construction of both a local and global interaction of the empirical distributions to compare. Globality naturally results from the Wasserstein distance, which is a metric on probability measures, and as such it measures discrepancy between distributions at whole level. Note however that this property would have been shared by any other metric on probability measures. Locality comes as a specific feature of regularized Wasserstein distance. Indeed as made clear by the solution in Eq. (4) of the entropy-smoothed optimal transport problem, weights \(T_{ij}\) tend to be larger for nearby points with an exponential decrease with respect to distance between \(\mathbf {P}\mathbf {x}_i\) and \(\mathbf {P}\mathbf {x}_{j'}\).

4.2 Regularized Wasserstein distance and Fisher criterion

Fisher criterion for measuring separability stands on the ratio of inter-class and intra-class variability of samples. However, this intra-class variability can be challenging to evaluate when information regarding probability distributions come only through empirical examples. Indeed, the classical \((\lambda = \infty )\) Wasserstein distance of a discrete distribution with itself is 0, as with any other metrics for empirical distributions. Recent result by Mueller and Jaakkola (2015) also suggests that even splitting examples from one given class and computing Wasserstein distance between resulting empirical distributions will result in arbitrary small distance with high probability. This is why entropy-regularized Wasserstein distance plays a key role in our algorithm, as to the best of our knowledge, no other metrics on empirical distributions would lead to relevant intra-class measures. Indeed, \(W_\lambda (\mathbf {P}\mathbf {X},\mathbf {P}\mathbf {X}) = \langle \mathbf {P}^\top \mathbf {P}, \mathbf {C}\rangle \) with \(\mathbf {C}= \sum _{i,j} T_{i,j} (\mathbf {x}_i - \mathbf {x}_j) (\mathbf {x}_i - \mathbf {x}_j)^T\). Hence, since \(\lambda < \infty \) ensures that mass of a given sample is split among its neighbours by the transport map \(\mathbf {T}\), \(W_\lambda (\mathbf {P}\mathbf {X},\mathbf {P}\mathbf {X})\) is thus non-zero and interestingly, it depends on a weighted covariance matrix \(\mathbf {C}\) which, because it depends on \(\mathbf {T}\), will put more emphasis on couples of neighbour examples.

More formally, we can show that minimizing \(W_\lambda (\mathbf {P}\mathbf {X},\mathbf {P}\mathbf {X})\) with respect to \(\mathbf {P}\) induces a neighbourhood preserving map \(\mathbf {P}\). This means that if an example i is closer to an example j than an example k in the original space, this relation should be preserved in the projected space. This implies that \(\Vert \mathbf {P}\mathbf {x}_i - \mathbf {P}\mathbf {x}_j\Vert _2\) should be smaller than \(\Vert \mathbf {P}\mathbf {x}_i - \mathbf {P}\mathbf {x}_k\Vert _2\). Then, this neighbourhood preservation can be enforced if \(K_{i,j} > K_{i,k}\), which is equivalent to \(M_{i,j} < M_{i,k}\), implies \(T_{i,j} > T_{i,k}\). Hence, since \(W_\lambda (\mathbf {P}\mathbf {X},\mathbf {P}\mathbf {X}) = \sum _{i,j} T_{i,j} \Vert \mathbf {P}\mathbf {x}_i - \mathbf {P}\mathbf {x}_j\Vert _2^2\), the inequality \(T_{i,j} > T_{i,k}\) means that examples that are close in the input space are encouraged to be close in the projected space. We show next that there exists situation in which this condition is guaranteed.

Proposition 1

Given \(\mathbf {T}\) the solution of the entropy-smoothed optimal transport problem, as defined in Eq. (3), between the empirical distribution \(\mathbf {P}\mathbf {X}\) on itself, \(\forall i,j,k\):

$$\begin{aligned} \exists \alpha \ge 1, K_{i,j}> \alpha K_{i,k}\quad \Rightarrow \quad T_{i,j} > T_{i,k} \end{aligned}$$

Proof

Because, we are interested in transporting \(\mathbf {P}\mathbf {X}\) on \(\mathbf {P}\mathbf {X}\), the resulting matrix \(\mathbf {K}\) is symmetric non-negative. Then, according to Lemma 1 (see “Appendix”), the solution matrix \(\mathbf {T}\) is also symmetric. Owing to this symmetry and the properties of the Sinkhorn–Knopp algorithm, it can be shown (Knight 2008) that there exists a non-negative vector \(\mathbf {v}\) such that \(T_{i,j} = K_{i,j} v_i v_j\). In addition, because this vector is the limit of a convergent sequence obtained by the Sinkhorn–Knopp algorithm, it is bounded. Let us denoted as A, a constant such that \(\forall i, v_i \ge A\). Furthermore, in Lemma 2 (see “Appendix”), we show that \(\forall i, 1 \ge v_i\). Now, it is easy to prove that

$$\begin{aligned} A> \frac{K_{i,k}}{K_{i,j}} \implies v_j \frac{K_{i,k}}{K_{i,j}} \implies K_{i,j} v_j - K_{i,k} > 0 \end{aligned}$$

and because \(\forall j,\, v_j \le 1\) and by definition \(T_{i,j} = v_i K_{i,j} v_j\), we thus have \( K_{i,j} v_j - K_{i,k}v_k> 0 \implies T_{i,j} > T_{i,k}\). In Proposition 1 we take \(\alpha =\frac{1}{A}\) since \(A<1\). \(\square \)

Note that this proposition provides us with a guarantee on a ratio \(\frac{K_{i,k}}{K_{i,j}}\) between examples that induces preservation of neighbourhood. However, the constant A we exhibit here is probably loose and thus, a larger ratio may still preserve locality.

4.3 Connection to Fisher discriminant analysis

We show next that WDA encompasses Fisher Discriminant analysis in the limit case where \(\lambda \) approaches 0. In this case, we can see from Eq. (3) that the matrix \(\mathbf {T}\) does not depends on the data. The solution \(\mathbf {T}\) for each Wasserstein distance is the matrix that maximizes entropy, namely the uniform probability distribution \(\mathbf {T}=\frac{1}{nm}{\mathbf {1}}_{n,m}\). The cross-covariance matrices become thus

$$\begin{aligned} \mathbf {C}^{c,c'}=\frac{1}{n_cn_{c'}}\sum _{i,j}( \mathbf {x}^c_i-\mathbf {x}^{c'}_j)( \mathbf {x}^c_i-\mathbf {x}^{c'}_j)^T \end{aligned}$$

and the matrices \(\mathbf {C}_w\) and \(\mathbf {C}_b\) correspond then to intra- and inter-class covariances as used in FDA. Since these matrices do not depend on \(\mathbf {P}\), the optimization problem (1) boils down to the usual Rayleigh quotient which can be solved using a generalized eigendecomposition of \(\mathbf {C}_w^{-1}\mathbf {C}_b\) as in FDA. Note that WDA is equivalent to FDA when the classes are balanced (in the unbalanced case one needs to weight the covarainces with the class ratios). Again, we stress out that beyond this limit case and when \(\lambda >0\), the smoothed optimal transport matrix \(\mathbf {T}\) promotes cross-covariance matrices that are estimated from local relations as illustrated in Fig. 1.

Following this connection, we want to stress again the role played by the within-class Wasserstein distances in WDA. At first, from a theoretical point of view, optimizing the ratio instead of just maximizing the between-class distance allows us to encompass well-known method such as FDA. Secondly, as we have shown in the previous subsection, minimizing the within-class distance provides interesting features such as neighbourhood preservation under mild condition.

Another intuitive benefit of minimizing the within-class distance is the following. Suppose we have several projection maps that lead to the same optimal transport matrix \(\mathbf {T}\). Since \(W_\lambda (\mathbf {P}\mathbf {X},\mathbf {P}\mathbf {X}) = \sum _{i,j} T_{i,j} \Vert \mathbf {P}\mathbf {x}_i - \mathbf {P}\mathbf {x}_j\Vert _2^2\) for any \(\mathbf {P}\), minimizing \(W_\lambda (\mathbf {P}\mathbf {X},\mathbf {P}\mathbf {X})\) with respect to \(\mathbf {P}\) means preferring the projection map that yields to the smaller weighted (according to \(\mathbf {T}\)) pairwise distance of samples in the projected space. Since for an example i, \(\{T_{i,j}\}_j\) are mainly non-zero among neighbours of i, minimizing the within-class distance favours projection maps that tend to tighly cluster points in the same class.

4.4 Relation to other information-theoretic discriminant analysis

Several information-theoretic criteria have been considered for discriminant analysis and dimensionality reduction. Compared to Fisher’s criteria, these ones have the advantage of going beyond a simple sketching of the data pdf based on second-order statistics. Two recent approaches are based on the idea of maximizing distance of probability distributions of data in the projection subspaces. They just differ in the choice of the metrics of pdf (one being a \(L_2\) distance (Emigh et al. 2015) and the second one being a Wasserstein distance (Mueller and Jaakkola 2015)). While our approach also seeks at finding projection that maximizes pdf distance, it has also the unique feature of finding projections that preserves neighbourhood. Other recent approaches have addressed the problem of supervised dimensionality reduction algorithms still from an information theoretic learning perspective but without directly maximizing distance of pdf in the projected subpaces. We discuss two methods to which we have compared with in the experimental analysis. The approach of Suzuki and Sugiyama (2013), denoted as LSDR, seeks at finding a low-rank subspace of inputs that contains sufficient information for predicting output values. In their works, the authors define the notion of sufficiency through conditional independence of the outputs and the inputs given the projected inputs and evaluate this measure through squared-loss mutual information. One major drawback of their approach is that they need to estimate a density ratio introducing thus an extra layer of complexity and an error-prone task. Similar idea has been investigated by Tangkaratt et al. (2015) as they used quadratic mutual information for evaluating statistical dependence between projected inputs and outputs (the method has been named LSQMI). While they avoid the estimation of density ratio, they still need to estimate derivatives of quadratic mutual information. Like our approach, the method of Giraldo and Principe (2013) avoids density estimation for performing supervised metric learning. Indeed, the key aspect of their work is to show that the Gram matrix of some data samples can be related to some information theoretic quantities such as conditional entropy without the need of estimating pdfs. Based on this finding, they introduced a metric learning approach, coined CEML, by minimizing conditional entropy between labels and projected samples. While their approach is appealing, we believe that a direct criterion such as Fisher’s is more relevant and robust for classification purposes, as proved in our experiments.

4.5 Wasserstein distances and machine learning

Wasserstein distances are mainly derived from the theory of optimal transport (Villani 2008), and provide a useful way to compare probability measures. Its practical deployment in machine learning problems has been alleviated thanks to regularized versions of the original problem (Cuturi 2013; Benamou et al. 2015). The geometry of the space of probability measures endowed with the Wasserstein metric allows to consider various objects of interest such as means or barycenters (Cuturi and Doucet 2014; Benamou et al. 2015), and has led to generalization of PCA in the space of probability measures (Seguy and Cuturi 2015). It has been considered in the problem of semi-supervised learning (Solomon et al. 2014), domain adaptation (Courty et al. 2016), or definition of loss functions (Frogner et al. 2015). More recently, it has also been considered in a subspace identification problem for analyzing the differences between distributions (Mueller and Jaakkola 2015), but contrary to our approach, they only consider projections to univariate distributions, and as such do not permit to find subspaces with dimension \(>1\). More recent works have proposed to use Wasserstein for measuring similarity between documents in Huang et al. (2016) and propose to learn a metric that encodes class information between samples. Note that in our work we use Wasserstein between the empirical distributions and not the training samples yielding a very different approach.

5 Numerical experiments

In this section we illustrate how WDA works on several learning problems. First, we evaluate our approach on a simple simulated dataset with a 2-dimensional discriminative subspace. Then, we benchmark WDA on MNIST and Caltech datasets with some pre-defined hyperparameter settings for methods having some. Unless specified and justified, for LFDA and LMNN, we have set the number of neighours to 5. For CEML, Gaussian kernel width \(\sigma \) has been fixed to \(\sqrt{p}\), which is the value used by Giraldo and Principe (2013) across all their experiments. For WDA, we have chosen \(\lambda = 0.01\) except for the toy problem. The final experiment compares performance of WDA and competitors on some UCI dataset problems, in which relevant parameters have been validated.

Note that in the spirit of reproducible research the code will be made available to the community and the Python implementation of WDA is available as part of the POT for Python Optimal Transport Toolbox (Flamary and Courty 2017) on Github.Footnote 1

5.1 Practical implementation

In order to make the method less sensitive to the dimension and scaling of the data, we propose to use a pre-computed adaptive regularization parameter for each Wasserstein distances in (1). Denote as \(\lambda _{c,c'}\) such parameter yielding thus to a distance \(W_{\lambda _{c,c'}}\). In practice, we initialize \(\mathbf {P}\) with the PCA projection, and define \(\lambda _{c,c'}\) as \(\lambda _{c,c'}=\lambda (\frac{1}{n_cn_{c'}}\sum _{i,j}\Vert \mathbf {P}x_i^c-\mathbf {P}x_j^{c'}\Vert ^2)^{-1}\) between class c and \(c'\). These values are computed a priori and fixed in the remaining iterations. They have the advantage to promote a similar regularization strength between inter and intra-class distances.

We have compared our WDA algorithms to some classical dimensionality reduction algorithms like PCA and FDA, to some locality preserving methods such as LFDA and LMNN and to some recent mutual information-based supervised dimensionality and metric learning algorithms such as LSDR and CEML mentioned above. For the last three methods, we have used the author’s implementations. We have also considered LSQMI as a competitor but did not report its performances as they were always worse than those of LSDR.

Fig. 2
figure 2

Illustration of subspace learning methods on a nonlinearly separable 3-class toy example of dimension \(d=10\) with 2 discriminant features (shown on the upper left) and 8 Gaussian noise features. Projections onto \(p=2\) of the test data are reported for several subspace estimation methods

Full size image

5.2 Simulated dataset

This dataset has been designed for evaluating the ability of a subspace method to uncover a discrimative linear subspace when the classes are non-linearly separable. It is a 3-class problem in dimension \(d=10\) with two discriminative dimensions, the remaining 8 containing Gaussian noise. In the 2 discriminant features, each class is composed of two modes as illustrated in the upper left part of Fig. 2.

Fig. 3
figure 3

Prediction error on the simulated dataset (left) with projection dimension fixed to \(p=2\) and error for varying K in the KNN classifier. (right) evolution of performance with different projection dimension p and best K in the KNN classifier

Full size image
Fig. 4
figure 4

Comparison of WDA performances on the simulated dataset (left) as a function of \(\lambda \). (right) as a function of \(\lambda \) and with different number of fixed point iterations

Full size image

Figure 2 also illustrates the projection of test samples in two-dimensional subspaces obtained from the different approaches. We can see that for this dataset WDA, LDSR and CEML lead to a good discriminant subspace. This illustrate the importance of estimating relations between samples in the projected space as opposed to the original space as done in LMNN and LFDA. Quantitative results are illustrated in Fig. 3 (left) where we reported prediction error for a K-Nearest-Neighbors classifier (KNN) for \(n=100\) training examples and \(n_t=5000\) test examples. In this simulation, all prediction errors are averaged over 20 data generations and the neighbors parameters of LMNN and LFDA have been selected empirically to maximize performances (respectively 5 for LMNN and 1 for LFDA). We can see in the left part of the figure that WDA, LDSR and CEML and to a lesser extent LMNN can estimate the relevant subspace, when the optimal dimension value is given to them,that is robust to the choice of K. Note that slightly better performances are achieved by LSDR and CEML. In the right plot of Fig. 3, we show the performances of all algorithms when varying the dimension of the projected space. We note that WDA, LMNN, LSDR and LFDA achieve their best performances for \(p=2\) and that prediction errors rapidly increase as p is misspecified. Instead, CEML performs very well for \(p \ge 2\). Being sensitive to the correct projected space dimensionality can be considered as an asset, as typically this dimension is to be optimized (e.g by cross-validation), making it easier to spot the best dimension reduction. At the contrary, CEML is robust to projected space dimensionality mis-specification at the expense of under-estimating the best reduction of dimension.

In the left plot for Fig. 4, we illustrate the sensitivity of WDA w.r.t. the regularization parameter \(\lambda \). WDA returns equivalently good performance on almost a full order of magnitude of \(\lambda \). This suggests that a coarse validation can be performed in practice. The right panel of Fig. 4 shows the performance of the WDA for different number of inner Sinkhorn iterations L. We can see that even if this parameter leads to different performances for large values of \(\lambda \), it is still possible find some \(\lambda \) that yield near best performance even for small value of L.

Fig. 5
figure 5

Averaged prediction error on MNIST with projection dimension (left) \(p=10\). (right) \(p=20\). In these plots, LSQMID has been omitted due to poor performances

Full size image
Fig. 6
figure 6

2D tSNE of the MNIST samples projected on \(p=10\) for different approaches. (first and third lines) training set (second and fourth lines) test set

Full size image
Fig. 7
figure 7

Averaged prediction error on the Caltech dataset along the projection dimension. In these plots, LSQMID has been omitted due to poor performances

Full size image

5.3 MNIST dataset

Our objective with this experiment is to measure how robust our approach is with only few training samples despite high-dimensionality of the problem. To this end, we draw \(n=1000\) samples for training and report the KNN prediction error as a function of k for the different subspace methods when projecting onto \(p=10\) and \(p=20\) dimensions (resp. left and right plots of Fig. 5). The reported scores are averages of 20 realizations of the same experiment. We also limit the analysis to \(L=10\) as the number of Sinkhorn fixed point iterations and \(\lambda =0.01\). For both p, WDA finds a better subspace than the original space which suggests that most of the discriminant information available in the training dataset has been correctly extracted. Conversely, the other approaches struggle to find a relevant subspace in this configuration. In addition to better prediction performance, we want to emphasize that in this configuration, WDA leads to a dramatic compression of the data from 784 to 10 or 20 features while preserving most of the discriminative information.

To gain a better understanding of the corresponding embedding, we have further projected the data from the 10-dimensional space to a 2-dimensional one using t-SNE (Van der Maaten and Hinton 2008). In order to make the embeddings comparable, we have used the same initializations of t-SNE for all methods. The resulting 2D projections on the test samples are shown in Fig. 6. We can clearly see the overfitting behaviour of FDA, LFDA, LMNN and LDSR that separate accurately the training samples but fail to separate the test samples. Instead, WDA is able to disentangle classes in the training set while preserving generalization abilities.

5.4 Caltech dataset

In this experiment, we use a subset described by Donahue et al. (2014) of the Caltech-256 image collection (Griffin et al. 2007). The dataset uses features that are the output of the DeCAF deep learning architecture (Donahue et al. 2014). More precisely, they are extracted as the sparse activation of the neurons from the 6th fully connected layer of a convolutional network trained on ImageNet and then fine-tuned for the considered visual recognition task. As such, they form vectors of 4096 dimensions and we are looking for subspace as small as 15. In this setting, 500 images are considered for training, and the remaining portion of the dataset for testing (623 images). There are 9 different classes in this dataset. We examine in this experiment how the proposed dimensionality reduction performs when changing the subspace dimensionality. For this problem, the regularization parameter \(\lambda \) of WDA was empirically set to \(10^{-2}\). The K in KNN was set to 3 which is a common standard setting for this classifier. The reported results reported in Fig. 7 are averaged over 10 realizations of the same experiment. When \(p\ge 5\), WDA already finds a subspace which gathers relevant discriminative information from the original space. In this experiment, LMNN yields to a better subspace for small p values while WDA is the best performing method for \(p\ge 6\). Those results highlight the potential interest for using WDA as linear dimensionality reduction layers in neural-nets architecture.

5.5 Running-time

For the above experiments on MNIST and Caltech, we have also evaluated the running times of the compared algorithms. The LFDA, LMNN, LDSR and CEML codes are the Matlab code that have been released by the authors. Our WDA code is Python-based and relies on the POT toolbox. All these codes have been runned on a 16-core Intel Xeon E5-2630 CPU, operating at 2.4 GHz with GNU/Linux and 144 Gb of RAM.

Running times needed for computing learned subspaces are reported in Table 1. We first remark that LSDR is not scalable. For instance, ot needs several tenths of hour for computing the projection from 4096 to 14 dimensions on Caltech. More generally, we can note that our WDA algorithm scales well and is cheaper to compute than LMNN and is far less expensive than CEML on our machine. We believe our WDA algorithm better leverages multi-core machines owing the large amount of matrix-vector multiplications needed for computing Sinkorhn iterations.

Table 1 Averaged running time in seconds of the different algorithms for computing the learned subspaces
Full size table

5.6 UCI datasets

Table 2 Average test errors over 20 trials on UCI datasets
Full size table

We have also compared the performances of the dimensionality reduction algorithms on some UCI benchmark datasets (Lichman 2013). The experimental setting is similar to the one proposed by the authors of LSQMI (Tangkaratt et al. 2015). For these UCI datasets, we have appended the original input features with some noise features of dimensionality 100. We have split the examples 50–50% in a training and test set. Hyper-parameters such as the number of neighbours for the KNN and and the dimensionality of the projection has been cross-validated on the training set and choosed respectively among the values [1 : 2 : 19] (in Matlab notation) and [5, 10, 15, 20, 25]. Splits have been performed 20 times. Note that we have also added experiments with Isolet, USPS, MNIST and Caltech datasets under this validation setting but without the additional noisy features. Table 2 presents the performance of competing methods. We note that our WDA is more robust than all other methods and is able to capture relevant information in the learned subspaces. Its average ranking on all datasets is 2.2 while the second best, LMNN is 3.4. There is only one dataset (vehicles) for which WDA performs significantly worse than top methods. Interestingly LSDR and LSQMI seem to be less robust than LMNN and FDA, against which they have not been compared in the original paper (Tangkaratt et al. 2015).

6 Conclusion

This work presents the Wasserstein Discriminant Analysis, a new and original linear discriminant subspace estimation method. Based on the framework of regularized Wasserstein distances, which measure a global similarity between empirical distributions, WDA operates by separating distributions of different classes in the subspace, while maintaining a coherent structure at a class level. To this extent, the use of regularization in the Wasserstein formulation allows to effectively bridge a gap between a global coherency and the local structure of the class manifold. This comes at a cost of a difficult optimization of a bi-level program, for which we proposed an efficient method based on automatic differentiation of the Sinkhorn algorithm. Numerical experiments show that the method performs well on a variety of features, including those obtained with a deep neural architecture. Future work will consider stochastic versions of the same approach in order to enhance further the ability of the method to handle large volume of high-dimensional data.