Learning to predict soccer results from relational data with gradient boosted trees

Abstract

We describe our winning solution to the 2017’s Soccer Prediction Challenge organized in conjunction with the MLJ’s special issue on Machine Learning for Soccer. The goal of the challenge was to predict outcomes of future matches within a selected time-frame from different leagues over the world. A dataset of over 200,000 past match outcomes was provided to the contestants. We experimented with both relational and feature-based methods to learn predictive models from the provided data. We employed relevant latent variables computable from the data, namely so called pi-ratings and also a rating based on the PageRank method. A method based on manually constructed features and the gradient boosted tree algorithm performed best on both the validation set and the challenge test set. We also discuss the validity of the assumption that probability predictions on the three ordinal match outcomes should be monotone, underlying the RPS measure of prediction quality.

1 Introduction

The goal of the challenge we tackled was to predict the outcomes of future soccer games, given past match outcome data. Soccer—the world-wide most popular sport—involves two teams of 11 players each, playing against each other in 90-min matches. The latter are distributed by teams’ country of origin and competence into leagues, and chronologically into seasons.

The goal of the Soccer Prediction Challenge 2017 was to evaluate multiple modeling approaches by their predictive performance. The test set was not only unavailable to the challenge participants but in fact non-existent at model-training time because the games in the test set had not been played yet.

The predictions were supposed to yield a probability for each possible outcome of a match. We approached the challenge by validating both relational and feature-based prediction approaches.

The provided data consist of over 200,000 soccer match results from different leagues all over the world over the course of the past 17 years.¹ While the amount of data is substantial, each record consisted solely of the names of the two teams and the final score. No additional features from the course of the game nor details about the teams’ players were available.

Such data inputs are rather modest, especially in the context of the feature-based modeling strategy. We thus put significant emphasis on hand-crafting new relevant features computable from such data. We followed our intuitive assumptions regarding various factors that commonly influence the outcome of a soccer match. Such factors were derived from the historical records of interactions between the teams. The statistics were computed using different levels of granularity in time and over different portions of the leagues. Also, subtle aspects such as the importance of a match were reflected as well.

In the modeling of latent variables, we also included successful elements from previous work reviewed hereafter. In particular, we employed the concept of team ratings (Hvattum and Arntzen 2010; Constantinou and Fenton 2013; Lasek et al. 2013; Van Haaren and Davis 2015), and in particular, we exploited the pi-rating concepts introduced by Constantinou and Fenton (2013). Secondly, the structure of the historical records can be viewed as a graph of teams connected through their matches played. This structural nature of sports contests has already been noted by Van Haaren and Van den Broeck (2015). We reflect the latter by exploring a relational modeling approach where the input data describe the graphical structure directly. However, we also exploit the relational structure in the feature-based approach through the PageRank algorithm, which has already been proposed in a similar context by Lazova and Basnarkov (2015).

As follows from the above, our main contribution lies in the careful feature-engineering process. On the other hand, regarding the structure of predictive models, we made no special assumptions and relied on standard machine-learning algorithms. These were namely the Gradient Boosted Trees (Friedman 2001) in the feature-based strategy, and the RDN-Boost  (Natarajan et al. 2012) algorithm in the relational case.

The rest of the paper is organized as follows. In the next section we give a brief account of related work. In Sect. 3 we describe the types of predictive models considered. Section 4 describes the features we constructed for the feature-based models. In Sect. 5 we validate the different modeling approaches on the disclosed data set. Section 6 provides a discussion of the principal trends observed in the experimental results. In Sect. 7 we summarize the conclusions, indicating the final model choice and its performance on the challenge test set. Finally, Sect. 8 suggests some directions for future work.

2 Related work

A number of authors including Constantinou et al. (2012), Oberstone (2009), Lago-Ballesteros and Lago-Peñas (2010), have explored ways to select or extract relevant variables for predictions of game outcomes in soccer and other team sports.

A distinguishing feature of the present challenge is that predictions can only be based on outcomes of previous matches rather than in-play or other detailed records. Other factors, which are unknown yet relevant for predictions, can be modeled as latent variables estimated from the data available. Such variables include various team ratings (Hvattum and Arntzen 2010; Constantinou and Fenton 2013). These methods were compared in Van Haaren and Davis (2015) and a review of other rating systems can be found in Lasek et al. (2013).

The rating system most prominent in the specific case of soccer is so-called pi-ratings introduced by Constantinou and Fenton (2013).

The structure of the historical records forms a large graph of teams connected through their matches played which suggest to exploit graph algorithms such as PageRank. This has been elaborated by Lazova and Basnarkov (2015).

Regarding the structure of the predictive models, statistical models have been mostly favored in previous work. This includes models based on Poisson distributions (Goddard 2005; McHale and Scarf 2007; Koopman and Lit 2015) and Bayes networks (Constantinou et al. 2012). Baio and Blangiardo (2010) combined ideas from both the latter approaches.

3 Predictive models

In what follows, the terms loss and win associated with a match refer to the home team’s outcome in that match, unless stated otherwise. Here we discuss the methods we used to estimate

$$\begin{aligned} (p_l, p_d, p_w) \in [0,1]^3 \text {, such that } p_l+p_d+p_w = 1 \end{aligned}$$

(1)

i.e., the probabilities of the three possible outcomes loss, draw, win of a given match.

3.1 Baseline predictors

We introduce two reference prediction policies, intended to act as natural upper and lower bounds on the prediction errors achievable with the trainable models introduced later.

The naive policy corresponding to the upper-bound predicts (1) for each match in a given season and league by setting $p_l$ to be the proportion of home-team losses in all matches of that league in the previous season, and similarly for $p_d$ and $p_w$. Intuitively, this predictor exploits the usual home-team advantage (Pollard and Pollard 2005), which is quantified into the probabilities using the relative frequencies from the immediately preceding season. Failing to improve on such a prediction policy would indicate a useless predictor.

The likely lower bound on prediction error is provided by bookmaker’s data. Bookmakers are considered a very reliable source of predictions (Forrest et al. 2005). Bookmaker’s odds represent inverted probability estimates of the outcomes. However, to get an edge over the market, the bookmaker employs a so-called margin, resulting in the inverted probabilities summing up to more than 1. Therefore we normalized the probability triple with a common divisor to make it sum up to one. For example if the odds for the home team to win, draw and lose are (respectively) 1.89, 3.13, 5, the implied inverted probabilities are $1.89^{-1}$, $3.13^{-1}$, $5^{-1}$, and the normalized probabilities are $1.89^{-1}/{Z}$, ${3.13^{-1}}/{Z}$, ${5^{-1}}/{Z}$ where $Z = 1.89^{-1} + 3.13^{-1} + 5^{-1}$. More advanced methods for deriving probabilities from the odds are described by Štrumbelj (2014). A bookmaker-based predictor was not allowed to infer predictions for the challenge’s test data, yet it still serves as a retrospective baseline. Improving on such a predictor is unlikely and would indicate a chance to become rich through sports betting.

3.2 Relational classification model

The present classification problem is essentially relational as the domain contains objects (teams, leagues, etc.) and relations among them (matches between teams, matches belonging to leagues, etc.). We thus wanted to explore a natively relational learner in such a setting.²

We sought a fast relational learning algorithm involving few or no hyper-parameters which produces probabilistic predictions. These conditions were met by the RDN-Boost algorithm (Natarajan et al. 2012). RDN-Boost is based on Relational Dependency Networks function approximators (Natarajan et al. 2010) which are learned in series, following a functional gradient boosting strategy.

Each learning sample for RDN-Boost consists of the target class indicator, and a ground relational structure (Herbrand interpretation) describing available historical (more precisely, from the 3-year interval just before the prediction time) facts on match outcomes and scores, and the match-team and match-league relationships. The specific categories of facts are listed in Table 1.

Furthermore, we included a hand-crafted piece of information (listed last in the table) indicating the pi-rating of a team at the time of a match. Pi-ratings are considered highly informative and capture both the current form and historical strengths of teams (Constantinou and Fenton 2013). The calculation principles of pi-ratings are relatively involved and we refer to the latter source for technical details. Informally, the idea of pi-ratings is that each team has its home and away rating. Based on the opposing teams’ ratings, the expected goal differences when playing against an average team are calculated and subtracted, obtaining the expected goal difference for the match. After the match has been played, the expected goal difference is compared with the observed goal difference. The margin of winning is less important than the actual outcome, therefore large wins/losses are discounted. The resulting error is then used to update the ratings according to the given learning rates. For the relational representation we considered the resulting home (away) rating of the home (away, respectively) team, and encoded the membership of each team into a discrete bin w.r.t. this rating.

Table 1 Types of ground facts used by the relational classification model

Since RDN-Boost provides binary classification models, we trained three separate models (one for each outcome, contrasting it with the other two) and normalized the probabilistic predictions to sum up to 1.

3.3 Feature-based classification model

An alternative approach assumes that features with non-structured values are first constructed from the original relational data, allowing the application of a conventional feature-based (or, attribute-value) machine-learning algorithm. Our requirements on such an algorithm include those stated in Sect. 3.2. However, the menu of attribute-value algorithms being much larger than in the relational case, we could afford further to require a natively multi-class classifier yielding a probability distribution on target classes, sparing us a post-processing step.

From among such eligible classifier types, we chose Gradient boosted trees (Friedman 2001). This choice was motivated by a multitude of machine learning competitions such as those hosted by Kaggle³ where the Gradient boosted trees algorithm, and specifically its Xgboost implementation (Chen and Guestrin 2016) turns out to be highly successful for problems of a similar character.⁴

3.4 Feature-based regression model

The loss function minimized by Xgboost during model fitting is the logarithmic loss, i.e., the sum over all training examples of log-probabilities assigned to the true classes of the examples. This loss function thus does not reflect the intuitive order

$$\begin{aligned} loss< draw < win \end{aligned}$$

(2)

on classes. However, the Xgboost algorithm can also be run in a regression mode, where the resulting model yields real numbers. We leveraged this mode to accommodate the order (2) by representing the three classes as 0, 0.5, 1, respectively. In the regression setting, the standard squared loss is minimized through training.

To map a model’s output $r \in [0;1]$ to the required distribution (1), we introduce an additional trainable model component. Specifically, we posit for each $i \in \{l,d,w\}$ that

$$\begin{aligned} p_i(r) = \frac{f_i(r)}{f_l(r)+f_d(r)+f_w(r)} \end{aligned}$$

(3)

where $f_i(r)$ is modeled as a beta distribution

$$\begin{aligned} f_i(r) = \mathrm {Beta}_{\mathbf {\Theta }}(r) \end{aligned}$$

(4)

in which the parameters $\mathbf {\Theta }$ maximize the function’s fit with tuples $r,P_i(r)$ available in training data; in particular, $P_i(r)$ is the proportion of training examples with outcome i among all examples for which the model yields r. Intuitively, e.g. $f_w(r)$ is an estimate of the win-probability for a match with regressor’s output r. Note that in general $f_l(r)+f_d(r)+f_w(r) \ne 1$, hence the normalization in (3).

3.5 Model portfolios

Here we address the heterogeneity among different soccer leagues by exploring model portfolios. Briefly, the set of all considered leagues is first split into relatively homogeneous partitions and a model is learned for each partition separately. The portfolio then collects all these models and for each prediction, it invokes only the applicable model. The type of the constituting models can be any of those described in the preceding sections.

The mentioned heterogeneity is due to several aspects. First of all, each league has a different structure. Most often each two teams from the same league play against each other two times in one season, once at each respective home stadium. But there are also leagues where two teams meet only once or where the teams are divided into groups and a team plays only other teams within the same group. Moreover, the number of teams that are promoted and relegated is also different for each league.

Besides the structural differences, the leagues differ in play-style. Some leagues favor offensive style while others play more defensive soccer, resulting in discrepancies in statistics like draw percentage, average number of scored goals (the latter shown in Fig. 1), etc. Moreover, the number of given yellow and red cards per match varies between leagues, possibly leading to larger changes in the team strengths between consecutive rounds, resulting from the offender being disqualified from one or more consecutive matches.

We tried three different ways to partition the league set. The first was to cluster the leagues according to the performance of a selected ‘ethalon’ predictor, dissecting the list of leagues sorted by this indicator into the tough group, the easy group, and so on, depending on the chosen granularity. The second approach was to cluster the leagues based on the leagues’ features using the standard k-means algorithm with the Euclidean metric on normalized numeric features. The last method was to train a separate model for each league.

Fig. 1

Overall average number of goals scored per match in different leagues

4 Data features

For the predictors in Sects. 3.3 and 3.4, we need a set of relevant features for each learning sample corresponding to a match. The set of features we constructed is listed in Table 2 and we describe their categories in turn. With exceptions indicated in the table, each feature relates to a team and so appears twice in the tuple describing a match, once for each of the two teams. The features are not evaluated for samples in the first two seasons due to the time lag required for some of them.

Table 2 Summary of constructed features. Except for the features shown in italics, each feature appears twice in the description of a sample; referring respectively to the home team and the away team, so there are 66 features in total. Note that the H and A prefixes refer to the home and away venues rather than teams

4.1 Historical strength

To reflect the long-term strength of the teams, we extracted means and variances of the scored and conceded goals, win percentages, and draw percentages. These statistics are calculated separately for matches played home and away as a team playing home is typically stronger than when playing away (Pollard and Pollard 2005).

The statistics are aggregated from the current and the two preceding seasons.

4.2 Current form

Even the strongest teams can have a period of weaker performance during a season and vice versa. Therefore we also include in the feature set a set of statistics similar to the above, except aggregated only over the last five matches played by the concerned team. If less than five matches have been played by the team in the current season, the feature is not evaluated and acquires a missing-value indicator. These statistics are not computed from home and away games separately as such split statistics would aggregate a very small number (2 or 3) of matches.

Additionally, the current strength of the team could be affected by the number of days since last match because of fatigue. Therefore the number of rest days is also included as a feature.

4.3 Pi-ratings

These features relate to the pi-ratings as explained in Sect. 3.2. Unlike in the logical representation used by the relational predictor, the present feature-based representation needs no discretization and thus we included directly the home and away ratings of each of the two teams and the predicted goal difference between the two.

4.4 PageRank

A drawback of the historical strength features is that they do not account for the opposing teams’ strengths in historical matches. A decisive win against a weaker opponent might not be as important as a close win against a title contender. To account for this factor, we utilized the PageRank (Lazova and Basnarkov 2015) algorithm. PageRank was originally developed for assessing the importance of a website by examining the importance of other websites referring to it. Similarly, our assumption was that a strong team would be determined by having better results against other strong teams.

The PageRank of a team can be computed out of a matrix with columns as well as rows corresponding to teams. Each cell holds a number expressing the relative dominance of one team over the other in terms of previous match outcomes. In particular, the i, j cell contains

$$\begin{aligned} \frac{3 w_{ij} + d_{ij}}{g_{ij}} \end{aligned}$$

(5)

where $w_{ij}$ ($d_{ij}$) is the number of wins (draws) of team i over (with) team j, and the normalizer $g_{ij}$ is the number of games played involving the two teams. These numbers are extracted from the current and the two preceding seasons. The coefficient 3 reflects the standard soccer point assignment.

In comparison with pi-ratings, PageRank does not work with the actual goal difference but solely with the match outcomes. The pi-ratings can experience larger changes after a single round, while the PageRank is calculated just form a slightly modified matrix. We thus consider PageRank a more regularized counterpart of pi-ratings.

4.5 Match importance

Match importance can be reasonably expected to affect players’ performance and so represents a relevant feature. It is however not obvious how to estimate it.

Match importance is closely tied with team’s rank and current league round. Adding the league round number to the feature vector is straightforward. However, dealing with team’s rank is more complicated. First of all, the ranking of teams with the same number of points is calculated by different rules in each league. More importantly, the ranking is often too crude to capture the match importance, because it neglects the point differences. For instance in a balanced league, a team can be in 5th place, trailing by only few points to the team in first place, with several rounds to go in the season, while in a league dominated by few teams, a team in 5th position would have no chance in the title race, reducing the importance of the remaining games. There were attempts to model the match importance by simulating the remaining matches of a season (Lahvička 2015). However, a quantity that can only follow from computational simulations can hardly be expected to affect the player’s mindsets.

We decided to extract the points from the league table, from which we subtracted the points of the team in question, obtaining relative point differences. The points are accumulated as the season goes on, and normalized by the number of games played so far. The relative point differences for team i were aggregated in vector $T_i(k)$ such that

$$\begin{aligned} T_i(k) = \frac{\pi _{\textsf {rank}(k)} - \pi _i}{g_i} \end{aligned}$$

(6)

where k ranges from 1 to the number of all teams in the league, $\pi _i$ ($\pi _{\textsf {rank}(k)}$) is the number of points team i (team ranked k-th, respectively) accumulated through the season, and $g_i$ is the number of games team i played.

To extend the feature set with a fixed number of scalars, we extracted only the first five and last five components of $T_i$ corresponding to the head and the tail of the ranking.

4.6 League

League-specific features consist of the numbers of teams, rounds, home win percentages, draw percentages, goal difference deviations, and home/away goals scored averages. These statistics are meant to provide a context for the historical strength features introduced earlier. For instance, scoring 2.5 goals per match on average has a different weight in a league where the average is 2 goals per match, and one with the average of 3 goals per match.

For an obvious reason, these features were not employed with models specific to a single league (c.f. Sect. 3.5).

5 Experimental evaluation

5.1 Validation and parameter tuning

The prediction evaluation measure of the organizers’ choice was the Ranked Probability Score. The latter was first described by Epstein (1969) and its use for evaluation of predictive models in soccer was proposed by Constantinou and Fenton (2012). It is calculated as

$$\begin{aligned} \mathrm {RPS}(p_1,\ldots p_{r-1},a_1,\ldots a_{r-1}) = \frac{1}{r-1} \sum _{i=1}^{r-1} \left( \sum _{j=1}^{i} \left( p_j - a_j\right) \right) ^2 \end{aligned}$$

(7)

where r is the number of possible outcomes ($r = 3$ in the case of soccer), $p_j$ is the predicted probability of outcome j so that $p_j \in [0,1]$ for $j = 1,2, \ldots r$ and $\sum _{k=1}^{r}p_k = 1$, and $a_j$ is the indicator of outcome j such that $a_j = 1$ if outcome j is realized and $a_j= 0$ otherwise.

Both the relational method (Sect. 3.2) and the feature-based methods (Sects. 3.3, 3.4) require to set a few hyper-parameters. In particular, for all of them the pi-ratings learning rates ($\lambda = 0.06, \gamma = 0.5$) need to be determined. The feature-based methods additionally require setting for the Xgboost’s parameters max_depth ($=4$), subsample ($=0.8$), min_child_weight ($=5$) and colsample_bytree ($=0.25$). The number of trees for Xgboost was determined using internal validation with early stopping. Two RDN-Boost parameters were tuned manually, number of trees ($=40$) and tree depth ($=5$).

For the relational method, we additionally tuned the discretization bins to encode the pi-ratings. The discretization bins were determined to hold the equal amount of teams using all data before season 2010/11. The rest of the parameters were tuned exhaustively through grid search, by training on the same data split, and validating on the remaining data excluding leagues not contained in the challenge test set. Ranges of values tried in the grid search were following: $\{3, 4, \ldots , 8\}$ for max_depth, $\{0.5, 0.6, \ldots , 1\}$ for subsample, $\{3, 4, \ldots , 8\}$ for min_child_weight, and $\{0.2, 0.25,\ldots , 0.5\}$ for colsample_bytree. For each of the three model classes, we picked the parameters minimizing the RPS on the validation set.

The training times for RDN-Boost model was on the order of weeks in comparison with a few hours for training the Xgboost model.

With the exception on Sect. 5.2, which follows a time-wise evaluation, all the reported RPS are averages over seasons 2010/11 and further, including only the leagues which were known to be included in the challenge test set. For each season from this validation period, the model was trained on all preceding seasons.

5.2 Model performance in time

Fig. 2

RPS of different types of predictive models over the course of several seasons (lower is better). Note the restricted scale on the vertical axis

Figure 2 shows the RPS values for successive seasons from the third season on, so that historical strength features can be calculated from a sufficient history. The RPS is calculated only on the leagues known to be included in the challenge test set.

We plot the RPS for two versions of the relational model (RDN-boost, c.f. Sect. 3.2), with and without access to the pi-ratings. This is to evaluate the value of the latter kind of information added to the otherwise ‘purely relational’ data. Furthermore, the two types of feature-based model types (regression, classification, c.f. Sects. 3.3, 3.4) are shown. We also plot the RPS a version of the feature-based classifier where only the pi-ratings are used for the predictions. Lastly, the upper-bound baseline (Sect. 3.1) is shown. The lower-bound baseline is not included as the bookmaker’s odds data are not available for all leagues; we shall compare to this baseline separately.

Each RPS value in the diagram pertains to the prediction made by a model trained on all data up to (and excluding) the current season, i.e. models are retrained at every season’s beginning. However, the relational models are an exception to this. Due to their high training runtimes, only a single model could be trained for each of the two relational variants: the training took place at the instant where the RND-boost plots begin. The same models were then used for subsequent predictions up to the 2016 mark, introducing a slight handicap for the relational models beyond the start of their plots.

A remark is in order regarding the training of the regression model. As explained earlier, besides fitting the regressor itself, we also need to train the mapping from its output to the predicted distribution. For the latter, as an over-fitting prevention measure, the proportions $P_i(r)$ (c.f. Sect. 3.4) are calculated as follows. When training the model for the n-th season, the r’s and the corresponding proportions $P_i(r)$ are collected from all of the preceding seasons; for each k-th ($k<n$) season, they are obtained with the model learned for that season (i.e., on data from seasons 1 to $k-1$), making predictions on the k-th season. This way, the proportions following from model predictions are collected from data not used for training the models.

5.3 Comparison to bookmaker’s predictions

For leagues where bookmaker’s odds are available, we compared the best performing model (i.e. the feature-based classification model) with a predictor implicitly defined by these odds as described in Sect. 3.1. We downloaded odds⁵ for more than 22000 matches for the 2008-2015 period.

Figure 3 shows the average RPS for the two predictors on individual leagues. Here, the classification model is trained as in Sect. 5.2, i.e. on all data preceding the season where prediction takes place.

It follows that the bookmaker completely dominates the learned classifier’s predictions. That is no surprise, given the additional sources of information available to the bookmaker. These include detailed play statistics collected from the matches, changes in teams’ rosters as well as video footages of the matches.

Fig. 3

RPS comparison of the feature-based classification model with the bookmaker’s predictions

5.4 Model portfolio performance

We assessed the potential of the portfolio strategy as described in Sect. 3.5. We first partitioned leagues according to predictability by a model. In particular, the leagues were ranked by the RPS achieved by the feature-based classification model validated in seasons 2007/08–2009/10 and trained on the preceding seasons. Then we split the list into 4 groups of 7 teams successive in this ranking. Next we produced an alternative partitioning by the League features (Table 2) through the standard k-means algorithm, setting $k=4$. We run the stochastic k-means algorithm several times and used the clustering consisting of most equally sized clusters. Lastly, we produced singleton clusters, one for each league. The groupings achieved by the former two approaches are summarized in Table 3.

Table 3 Clusters obtained by clustering the leagues by performance and by feature similarity

We trained the portfolio model using the feature-based classifier as the constituting model type. Table 4 presents the RPS for the three clustering variants, with models trained on seasons up to and including 2009/10 and validated on all the subsequent seasons. The results indicate a detrimental effect of each clustering variant, likely following from the smaller training sets available for training each constituting model.

Table 4 RPS of a portfolio model with different league partitionings

5.5 Feature importance

Lastly, we examined the effect of individual feature categories as defined in Sect. 4. We did this in two manners.

Firstly, we counted how many times a feature was used in the tree nodes of the classification model. Figure 4 shows that the pi-ratings were by far the most commonly used features. On the other hand, current-form features were used only sporadically.

Fig. 4

Average occurrence counts of features of given categories in the classification trees’ nodes

Secondly, we trained the model (again on seasons up to and including 2009/10) using different feature subsets and compared their RPS (on the remaining seasons). As Table 5 shows, each feature set extension leads to a small improvement of the model’s performance.

Table 5 Performance of the classification model trained on different subsets of features

6 Discussion

We discuss here the principal trends observed from the experimental results.

First, as expected, all predictions methods fell between the natural lower and upper bounds in terms of the RPS error indicator.

Second, quite surprisingly, the performance of the relational model was not far from that of the best predictor despite working with ‘all-inclusive’ data inputs with no expert hints, except for the pi-ratings in one of its two versions. However, the classifier based on features manually designed with domain insight still turned out unmatched in performance.

Third, the regression model performed rather poorly. This model was intended to accommodate the ordinality of target classes (2). We analyzed its predictions and indeed, the predicted probabilities were always monotone in the sense that either $p_l \le p_d \le p_w$ or $p_l \ge p_d \ge p_w$. However, the best-performing classification model did not adhere to such ordinality. In particular the latter model predicted the draw as the least probable outcome in about 30 % of the matches. This calls into question the monotonicity assumption and consequently the suitability of the RPS evaluation measure.

To get further insight into this issue, we analyzed the bookmaker’s predictions and found out that the predicted draw probability is smallest among the three predicted probabilities in about 25 % of the matches, further supporting the reasonability of predicting non-monotone probability distributions.

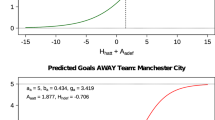
In fact, although the very outcomes of a game are naturally ordered, the corresponding probabilities cannot be reasonably expected to be monotone. Indeed, for a pair of equal-strength teams, the draw is the least probable match outcome. This is given by the prior probability of results which is much lower for draws. As the number of goals in a match increases, the number of possible draws grows linearly, while the number of all possible results grows quadratically. As we can observe from the Fig. 5, this scenario indeed occurs when the probabilities of the home team winning and losing are close to each other, or in other words, when there is no clear favorite.

Fig. 5

Distribution of the classification model’s (left) and bookmaker’s (right) probability predictions on the $p_w$-$p_l$ plane. Green dots indicate the cases where $p_d$ is smaller than each of $p_w$ and $p_l$ (Color figure online)

Another reason why the draw might be the least probable outcome is that the teams are usually awarded 3 points for a win and 1 point for a draw. In certain situations, a team (or both competing teams) might consider the draw as a loss of two points instead of a gain of one point. This leads to taking a higher risk during a match when the score is level.

7 Conclusions

To produce predictions for the challenge test set, we chose the feature-based classification model, which achieved the smallest average RPS of 0.2055 on the validation set. Its RPS on the challenge test set was 0.2063, making it the winning predictor of the contest.

We analyzed the model’s predictions and came up with an interesting observation that in about 30% of matches, the draw was the least probable outcome, and therefore the outcome probabilities were not monotone as expected by the employed RPS metric.

8 Future work

Although the feature-based classifier was the model of final choice, we see only little room for its improvements through designing new features. Indeed, our investigation in this direction has already been quite thorough, with each new feature providing just a very small edge on the previous. Most of the prediction performance can be attributed to the complex rating metrics, i.e. the pi-ratings and the PageRank, which renders these the most promising line of future research. Other than augmenting the feature set, possible improvements may be achieved by smarter ways to aggregate data towards the feature values. For example,⁶ weighting the aggregated data by their recency could lead to more informative statistics.

The relational model was not able to match the performance of the approach based on manually constructed features. However, given its generality, we find its performance rather encouraging. Further improvements in this respect could be achieved by including expert guidance in the formation of relevant relational concepts while maintaining the expressiveness and generality of the relational approach. This could be assisted by active learning strategies$^{6}$ such as the recent method by Odom and Natarajan (2016).

Lastly, from the perspective of soccer outcome prediction modeling, it would be interesting to conduct a more thorough analysis of the individual constructed features towards the prediction performance. In particular, our basic analysis from Sect. 5.5 could be extended by identifying features in the tree model which are conditionally important, given the occurrences of specific features at higher levels of the tree.$^{6}$

Appendix A.

See Table 6.

Table 6 Comparison of models’ RPS in different leagues