Online multi-label dependency topic models for text classification

Abstract

Multi-label text classification is an increasingly important field as large amounts of text data are available and extracting relevant information is important in many application contexts. Probabilistic generative models are the basis of a number of popular text mining methods such as Naive Bayes or Latent Dirichlet Allocation. However, Bayesian models for multi-label text classification often are overly complicated to account for label dependencies and skewed label frequencies while at the same time preventing overfitting. To solve this problem we employ the same technique that contributed to the success of deep learning in recent years: greedy layer-wise training. Applying this technique in the supervised setting prevents overfitting and leads to better classification accuracy. The intuition behind this approach is to learn the labels first and subsequently add a more abstract layer to represent dependencies among the labels. This allows using a relatively simple hierarchical topic model which can easily be adapted to the online setting. We show that our method successfully models dependencies online for large-scale multi-label datasets with many labels and improves over the baseline method not modeling dependencies. The same strategy, layer-wise greedy training, also makes the batch variant competitive with existing more complex multi-label topic models.

1 Introduction

Multi-label classification is the problem where each instance in a dataset is assigned multiple labels. Typical application areas include texts, images, and biological datasets. In this paper we focus on text datasets, in particular, datasets with many labels. While there is considerable work on datasets with a moderate amount of labels, meaning several tens or hundreds of labels at the most, dealing with larger label numbers is problematic for many multi-label methods. However, in real world datasets, there often are large amounts of labels with skewed frequencies. This poses a problem for most multi-label methods.

An important feature of multi-label datasets is that labels often exhibit dependencies. Assume for example that a text has two labels, “Language” and “Programming”. This could mean the text is about programming languages, showing that there is some overlap between the two labels. Therefore there is a certain dependency between them, one that is perhaps not exhibited by labels such as “Dog” and “Matrices”. A text about dogs is unlikely to also be about matrices, whereas a text about languages has a certain probability to also be about programming. Therefore, modeling dependencies has the potential to improve the accuracy of multi-label classifiers. The potential improvement is expected to be higher when the amount of training data for one of the labels is limited. For example if there are only few documents on programming, but a lot of documents about languages, the dependency between those labels could enhance the prediction of new documents about programming. One could understand this as providing additional positive examples that describe a certain aspect of documents about programming. A model that does not use dependencies only has the few programming documents as positive examples. Experimental evidence by Read et al. (2011) suggests that in cases where large numbers of training examples are available, the modeling of label dependencies may be unnecessary or in some cases even detrimental. In the streaming setting we deal with large amounts of training data, however, in real world data sets most labels are rare and only few labels are very frequent. This means that despite the large amount of data, the modeling of label dependencies might be extremely important if the number of labels is high enough.

Fig. 1

Word clouds for the Ohsumed dataset after training for 100 iterations using SCVB-Dep.. The size of the words is scaled according to their frequencies. Each word cloud corresponds to one label and includes the 30 most frequent words for this label. The labels shown are a antibiotics, b multiple abnormalities, c adenocarcinoma, d adrenal cortex hormones, e aerosols, f alopecia

The method we propose in this paper is based on topic modeling using latent Dirichlet allocation (LDA). The underlying multi-label approach was originally introduced as LabeledLDA (LLDA) (Ramage et al. 2009) and not only has a competitive performance, but also the advantage of interpretability of the resulting model. We can extract word clouds for each label and human feedback may be incorporated in the priors of this generative model. The method was extended to Dependency-LDA (Dep.-LLDA) by Rubin et al. (2012), who incorporated the modeling of label dependencies to develop a method that is competitive with state-of-the-art discriminative SVM-based methods. However, their method is a complex model with many parameters and it is not usable in an online setting.

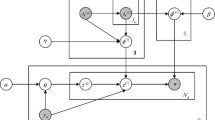
In this paper we propose a simplified version of Dependency-LDA to yield a practically more appealing and well performing model that may be used in the batch as well as the online setting. To make this simplification possible without sacrificing classification accuracy, our method uses a greedy training strategy inspired by recent advances in neural networks training to train the model one layer at a time. Similarly to boosting, the label level is learned on the input directly while the next layer receives the output of the label level as input. Thereby, two models are essentially stacked on top of each other during training and combined into one larger model during inference. This approach can be justified by considering that the first level learns the connection between labels and words where the labels are given during training (see Figs. 1 and 2), whereas the higher level learns more abstract label dependencies (see Figs. 3 and 4 for an example of learned label dependencies).

Fig. 2

Word clouds for the Amazon dataset after training for 100 iterations using SCVB-Dep.. The size of the words is scaled according to their frequencies. Each word cloud corresponds to one label and includes the 30 most frequent words for this label. The labels shown are a breakfast and cereal bars, b small animals, c tourist destinations and museums, d vegetables, e assessment, f atlases and maps

Fig. 3

Label clouds for the Ohsumed dataset after training for 100 iterations using SCVB-Dep.. The size of the labels is scaled according to their frequencies. Each label cloud corresponds to one topic and includes the 30 most frequent labels for this topic

Fig. 4

Label clouds for the Amazon dataset after training for 100 iterations using SCVB-Dep.. The size of the labels is scaled according to their frequencies. Each label cloud corresponds to one topic and includes the 30 most frequent labels for this topic

An example for an application area of online multi-label classification based on topic modeling is the monitoring of news as they appear everyday. Our topic modeling method allows the classification of newly arriving documents into predetermined categories, but also to extract word clouds from each topic and thus identify terms or aspects that become relevant over time. Furthermore, the model can be updated with new training data at any time. The feasibility of such an approach has already been shown for unsupervised topic modeling (AlSumait et al. 2008), however, until now an online supervised multi-label topic modeling approach that models label dependencies is not available to our knowledge.

Our contributions are as follows: First, we introduce a new LDA topic model that models label dependencies and can be used on streaming data. Second, we provide Gibbs sampling equations for the batch version as well as variational Bayes update equations for the online version of our method. Third, we show that this model is competitive with the previously existing models in modeling label dependencies in the batch as well as the online setting on a range of publicly available large-scale multi-label text datasets with thousands of labels.

2 Related work

The main challenge in multi-label classification is the exploitation of label dependencies. Accordingly, Zhang and Zhou (2014) divide multi-label algorithms into three families. The first-order strategy ignores dependencies and considers each label separately. Second-order strategies consider pairwise dependencies between labels, e.g. by considering a ranking between relevant and irrelevant labels. High-order strategies allow modeling of high-order relations between labels. Classifier chains (Read et al. 2011) and RAKEL (RAndom k-LabELsets) (Tsoumakas and Vlahavas 2007) are among the most popular high-order methods. Other notable examples for high-order strategies include work by Ghamrawi and McCallum (2005), who propose to learn label dependencies using conditional random fields and a Bayesian network model of the label dependencies by Zhang and Zhang (2010). Learning one global model of label dependencies may lead to overgeneralization in some cases, which is why (Huang and Zhou 2012) introduced a model to learn local label correlations by considering instance similarity in addition to global label dependencies. While high-order strategies can model complex label dependencies, they are typically computationally more expensive and do not scale well.

Multi-label classification algorithms are also commonly divided into two different types (Tsoumakas and Katakis 2007): problem transformation methods and algorithm adaptation methods. Problem transformation methods transform the multi-label classification problem into a combination of single-label classification problems, e.g. each label or each label set is predicted by a separate classifier. Algorithm adaptation methods adapt an algorithm to directly solve the multi-label classification problem. Our algorithm is a variant of the algorithm adaptation type since we only learn one model specifically for the multi-label task. One of the most efficient and prominent multi-label classifiers is the Binary Relevance (BR) method (Tsoumakas and Katakis 2007), a problem transformation method that learns one classifier for each label and combines the predictions of all classifiers into a multi-label prediction. This approach is simple yet often surprisingly effective, especially when a large amount of training data is available for each label (Read et al. 2011). However, BR does not take label dependencies into account. Nevertheless, it is considered a standard baseline method in this field. While BR is considered to be an efficient and scalable classifier, it still requires to learn one classifier per label which can lead to very large models. Most multi-label algorithms in the literature are even more inefficient, many have a complexity that is quadratic in the number of labels [see e.g. Zhang and Zhou (2014), Wicker et al. (2012)], and therefore are not applicable in the kind of large-scale setting we consider here. Recently, there have also been some approaches using deep learning and neural networks, but none of them scales well with very large label numbers (Wicker et al. 2016; Gouk et al. 2016; Zhang et al. 2017; Nam et al. 2014).

In light of these issues, a new line of work on so-called extreme multi-label classification has developed in recent years. This work is concerned with datasets having several hundred thousand or even millions of labels and features. For example, FastXML (Fast eXtreme Multi Label) by Prabhu and Varma (2014), an ensemble of decision trees, has prediction cost that is logarithmic in the number of labels. Another method, PD Sparse (Primal Dual Sparse approach to extreme multiclass and multilabel classification) by Yen et al. (2016) has a training runtime sublinear in the number of classes or labels. Although we compare to these two methods, our setting is a medium-large-scale setting as compared to the extreme large-scale setting where these methods are applicable.

The first notable method to do multi-label classification based on latent Dirichlet allocation (LDA) was the LabeledLDA (LLDA) model by Ramage et al. (2009). This work simply builds a topic model where each topic corresponds to one label resulting in just one model for all labels that can be trained and tested in feasible amounts of time. Each document has a distribution $\theta$ over its labels that can be used for prediction. Furthermore, the method can be used to extract relevant parts of a document for a specific label and to learn word distributions for the different labels. It is suitable for large collections of data since the training can efficiently be performed using Gibbs sampling. LLDA is therefore a simple and efficient method with many advantages. Another related LDA method is the author-topic model by Rosen-Zvi et al. (2004). It is used to model distributions over topics for different authors. It has not been used for classification, however, it has strong similarities to our model. Instead of modeling distributions over topics for different authors, our model learns distributions over labels for different topics and incorporates a document-topic distribution. We show in Sect. 4.4 that our model is in fact a generalization of the author-topic model. A related although unsupervised model is PAM (Li and McCallum 2006), which models topic correlations, however in contrast to our model it learns correlations for each document separately, which makes hyperparameter optimization a necessity.

The main shortcoming of LLDA is its failure to model label dependencies. This was addressed by Rubin et al. (2012), who introduced Dependency-LDA (Dep.-LLDA), which we will discuss in more detail in the following section. Dep.-LLDA consistently outperforms LLDA in terms of classification performance, however, it also has a larger runtime and many parameters. Our Fast-Dep.-LLDA addresses these shortcomings since it is simpler, has fewer parameters, is usable in an online setting and has a competitive classification performance.

For LDA there exists an online variant for streaming data based on variational Bayes introduced by Hoffman et al. (2010, 2013). Teh et al. (2006b) and Asuncion et al. (2009) improved this work by collapsing out the latent variables. Foulds et al. (2013) combine the online part of Hoffman et al. and Capp and Moulines (2009), and the collapsing part of Asuncion et al., resulting in an online stochastic collapsed variational Bayes (SCVB) with improved performance.

Using these online variational Bayes methods one can perform online multi-label classification in the same way as LLDA performs batch classification. We develop a collapsed variational Bayes formulation for our Fast-Dep.-LLDA, called SCVB-Dep., that allows online training while learning label dependencies. This is in contrast to Rubin et al.’s Dep.-LLDA, for which no such formulation exists.

3 Background

In this section we introduce Dep.-LLDA, a topic model for multi-label classification introduced by Rubin et al. (2012). The notation is summarized in Table 1. Our proposed method is an improved version of this model. The idea of Dep.-LLDA is to learn a model with two types of latent variables: the labels and the topics. The labels are associated with distributions over words (see, e.g., Figs. 1 and 2), while the topics are associated with distributions over labels (see, e.g., Figs. 3 and 4). The topics capture dependencies between the labels since the frequent labels in one topic are labels that tend to co-occur in the training data.

Table 1 Notation for Dep.-LLDA Gibbs sampling models

The generative process for Dep.-LLDA is given as follows:

• 1. For each topic $t\in T$ sample a distribution over labels $\phi '_t \sim Dirichlet(\beta _Y)$

• 2. For each label $y\in Y$ sample a distribution over words $\phi _y \sim Dirichlet(\beta )$

• 3. For each document $d\in D$:

  • (a) Sample a distribution over topics $\theta ' \sim Dirichlet(\gamma )$

  • (b) For each label token in d:

    • i. Sample a topic $z'\sim Multinomial(\theta ')$

    • ii. Sample a label $c\sim Multinomial(\phi '_{z'})$

  • (c) Sample a distribution $\theta \sim Dirichlet(\alpha ')$

  • (d) For each word token in d:

    • i. Sample a label $z\sim Multinomial(\theta )$

    • ii. Sample a word $w\sim Multinomial(\phi _z)$

The Gibbs sampling equations for the labels z and the topics $z'$ are given by:

$$\begin{aligned}&P\left( z=y|w,z_{-i},z'_{-i}\right) \propto \frac{n^{w_i}_{-iy}+\beta }{n^{.}_{-iy}+|W| \beta }\left( n^{d}_{-iy}+\alpha '\right) \end{aligned}$$

(1)

$$\begin{aligned}&P\left( z'=k|c=y,c_{-i},z'_{-i}\right) \propto \frac{n^{y}_{-ik}+\beta _y}{n^{.}_{-ik}+|Y| \beta _y}\left( n^{d}_{-ik}+\gamma \right) , \end{aligned}$$

(2)

where $n^{w_i}_{-iy}$ is the number of times word $w_i$ occurs with label y. $n^{.}_{-iy}$ is the number of times label y occurs overall, $n^{d}_{-iy}$ is the number of times label y occurs in the current document, $n^{y}_{-ik}$ is the number of times label y occurs with topic k, $n^{.}_{-ik}$ is the number of times topic k occurs overall and $n^{d}_{-ik}$ is the number of times topic k occurs in document d. The subscript $-i$ indicates that the current token is excluded from the count.

The connection between the labels and the topics is made through the prior $\alpha '$. To calculate $\alpha '$, Rubin et al. propose to make use of the label tokens c. According to these $M_d$ label tokens $\alpha '$ for document d is calculated as follows:

$$\begin{aligned} \alpha '=\left[ \eta \frac{n^{d}_{1}}{M_d}+\alpha ,\eta \frac{n^{d}_{2}}{M_d}+\alpha ,\ldots ,\eta \frac{n^{d}_{|Y|}}{M_d}+\alpha \right] , \end{aligned}$$

(3)

where $n^{d}_{y}$ is set to one during training, and to the number of times a particular label was sampled during testing, and $\eta$ and $\alpha$ are parameters.

During testing however, instead of taking M samples and calculating $\alpha '$ as described above, a so-called “fast” inference method is used. This means $\alpha '$ is calculated as follows:

$$\begin{aligned} \alpha '=\eta {\hat{\theta }}'{\hat{\phi }}'+\alpha , \end{aligned}$$

(4)

where ${\hat{\phi }}$ and ${\hat{\theta }}$ are the current estimates of $\phi$ and $\theta$. Because there are no label tokens during testing, the sampled z variables are used directly instead of c. During training, since the labels of each document are given, $\phi$ and $\phi '$ are conditionally independent which allows separate training of both parts of the topic model. Finally, they apply a heuristic to scale $\alpha '$ according to the document length during testing.

4 Proposed method

4.1 Fast-Dep.-LLDA

Our proposed Fast-Dep.-LLDA and Dep.-LLDA have strong similarities. The main difference is the omission of $\theta$ and $\alpha '$ in our model. Both models learn the label dependencies through the label-topic distributions $\phi '$. Dep.-LLDA passes the dependency information down via the label-prior $\alpha '$ and the label distribution $\theta$. Our model, however, takes the more direct approach of generating the labels from $\phi '$ directly instead of using the intermediary distribution $\theta$ (see the graphical models in Fig. 5a, c). Thereby Fast-Dep.-LLDA avoids a couple of heuristics that are employed by Dep.-LLDA:

• 1. Dep.-LLDA does not perform the calculation of the parameter $\alpha '$ according to the proposed model, but rather a fast inference method is used that was empirically found to be faster and was leading to more accurate results.

• 2. The calculation of the parameter $\alpha '$ itself involves two parameters $\eta$ and $\gamma$ that are determined heuristically by the authors. It is unclear how these parameters could be estimated from the data, except by doing expensive grid search.

• 3. During evaluation the parameter $\alpha '$ is scaled according to the document length.

• 4. During evaluation, the label tokens c and in particular the number of labels are unknown. To circumvent this problem, the authors replace the label tokens c by the label indicator variables z during testing, thereby assuming that the number of labels is equal to the document length.

Fig. 5

The graphical models of a Dep.-LLDA from Rubin et al. (2012), b PAM (Li and McCallum 2006), c our Fast-Dep.-LLDA

The full generative process of our model is given in Table 2. Each document is only associated with one document-specific distribution $\theta '$ over the topics. In comparison, Dependency-LDA has two document-specific distributions, $\theta$ and $\theta '$, where $\theta$ is a label distribution. The label distribution $\theta$ is implicitly contained in our model and can be obtained by multiplying the document-specific topic distributions $\theta '$ with the global topic-label distributions $\phi '$.

From the graphical model and the generative process we have the joint distribution of Fast-Dep.-LLDA given by:

$$\begin{aligned} P(w,z,z')=P(w|z,\phi )P(z|z',\phi ')P(z'|\theta ') \end{aligned}$$

(5)

To obtain a collapsed Gibbs sampler, we have to integrate out $\phi$, $\phi '$, and $\theta '$ from the three conditional probabilities respectively. The integrals can be performed separately as in Griffiths and Steyvers (2004), resulting in the following conditional distribution for the latent variables z and $z'$:

$$\begin{aligned} P\left( z=y,z'=k|w,z_{-i},z'_{-i}\right) \propto \frac{n^{w_i}_{-iy}+\beta }{n^{.}_{-iy}+|W| \beta }\frac{n^{y}_{-ik}+\beta _y}{n^{.}_{-ik}+|Y|\beta _y}\left( n^{d}_{-ik}+\alpha \right) \end{aligned}$$

(6)

This sampling equation results in a blocked Gibbs sampler that samples two variables at a time instead of just one: each word is assigned a topic and a label. For our model we propose to use a basic Gibbs sampler that only samples one variable at a time instead. This may have the disadvantage of making successive samples more dependent (Bishop 2006), but we find that the advantages outweigh this potential disadvantage. Mainly, the sampling complexity is reduced from O(|T| |Y|) to $O(|T|+|Y|)$. Also, it makes more sense in our case to view each document as a whole entity and sample the variables in a top down manner (see Fig. 2). First, more abstract topics are sampled (line 3–5, Eq. 8), representing the label dependencies of the document, and second, the labels are sampled based on these document-specific label dependencies (line 6–8, Eq. 7).

Table 2 The generative process of Fast-Dep.-LLDA

The corresponding sampling equations for the alternate sampling of labels and topics are given as follows. Given $z'$, the equation for sampling z is:

$$\begin{aligned} P\left( z=y|w,z'=k,z_{-i},z'_{-i}\right) \propto \frac{n^{w_i}_{-iy}+\beta }{n^{.}_{-iy}+|W| \beta }\left( n^{y}_{-ik}+\beta _y\right) \end{aligned}$$

(7)

The sampling equation for $z'$ follows from $P(z'|z)=\frac{P(z,z')}{\sum _{z'}{P(z,z')}}$, where $P(z,z')=P(z|z',\phi ')P(z'|\theta ')$. The same steps as for sampling z apply, giving:

$$\begin{aligned} P\left( z'=k|z=y,z_{-i},z'_{-i}\right) \propto \frac{n^{y}_{-ik}+\beta _y}{n^{.}_{-ik}+|Y|\beta _y}\left( n^{d}_{-ik}+\alpha \right) . \end{aligned}$$

(8)

4.2 Greedy layer-wise training

Intuitively, the model cannot benefit from a prior on the label distribution if the prior is an untrained model of label dependencies. The abstract level of label dependencies has to be trained first, before we can use it as a prior, otherwise the model is more likely to be “confused” by the untrained prior.

Another view is to consider the “explaining away” effect as the problem. If a document is well explained by a certain label, other labels become less likely. In supervised learning, the labels that explain the document are given and ideally all of them should contribute to the document-label distribution. Gibbs sampling can lead to certain labels being sampled extremely rarely or not at all if the document is well explained by a subset of the documents labels. During training this can be a problem, since similar labels become anti-correlated through the observed words whereas in fact they are often correlated.

Instead of training the complete model at once, we propose a greedy layer-wise training procedure inspired by Hinton et al. (2006) and Bengio et al. (2007). This means we begin by training the label layer using Eq. (7). Since the topic-label distributions $\phi '$ are not trained yet, we assume they form a uniform prior on the label assignments z such that $P(z|w)\propto P(w|z)$. This leads to the following equation for sampling label assignments z during training of Fast-Dep.-LLDA:

$$\begin{aligned} P\left( z=y|w,z'=k,z_{-i},z'_{-i}\right) \propto \quad \frac{n^{w_i}_{-iy}+\beta }{n^{.}_{-iy}+|W| \beta } \end{aligned}$$

(9)

Fig. 6

The pseudo code for batch Fast-Dep.-LLDA. a Greedy Algorithm, b Non-Greedy Algorithm

The model is guaranteed to converge to the optimum given the chosen parameters. The greedy model may be viewed as letting $\sum _y\beta _y\rightarrow \infty$ which means the Dirichlet becomes a uniform distribution in case of symmetric $\beta _y$. Greedy training corresponds to choosing the most extreme parameter value for $\beta _y$, which leads to the second term vanishing from Eq. (7) completely. Empirically, we found that on all tested multi-label datasets the convergence was better using greedy training than non-greedy training (compare the algorithms in Fig. 6). As Fig. 7 shows for the EUR Lex datasets, the testset loglikelihood increases for the greedy training procedure. For the non-greedy training procedure, the likelihood increases at first, but then decreases slightly and remains at a much lower level. We suspect that this effect is due to overfitting caused by the highly constrained supervised training. The greedy training can be viewed as performing a kind of regularization by imposing a simplified prior during the training of the lower level of the model.

As Hinton et al. note, in the supervised setting each label only provides a few bits of constraints on the parameters which makes overfitting a much bigger problem than underfitting and going back to retrain the first level given the information from the topic level is likely to do more harm than good. The procedure is also similar to boosting in that weak models are stacked on top of each other, using the output of the previous models. Going back to improve earlier models based on later ones is not likely to do the model any good. Dep.-LLDA inadvertently also employed this principle by training the two parts of the model separately. As our model shows, it is however not necessary to plug in a completely observed variable c and make the two parts conditionally independent (see Fig. 5a).

Following Bengio et al. we train the two layers at the same time while still maintaining the greedy idea. By sampling with the above equation, the parameters of both layers are learned together, meaning, the second layer can immediately start training on the output of the first layer. This means we do not have to pick two separate parameters for the number of training iterations.

Fig. 7

Testset loglikelihood on the EUR Lex dataset for the greedy and the non-greedy version of our method. For the non-greedy version we chose $\beta _y=0.01$

The analogy to Hinton’s layer-wise greedy training is rather loose and, to our knowledge, without a formal, mathematical connection: Both methods rely on the same idea, however, our method does not have a theoretical justification in terms of complimentary priors or convergence guarantees based on variational bounds. Both methods are based on the idea of training a hierarchical generative model in a greedy, layer-wise manner. Both methods perform well empirically as compared to their non-greedy counterparts. Thus, we do not claim any connection that goes deeper than that one method being loosely inspired by the other.

Overall we derived a compact model named Fast-Dep.-LLDA with only three parameters, $\alpha$, $\beta$, and $\beta _y$, and an efficient Gibbs sampler with a greedy layer-wise training procedure.

4.3 Online Fast-Dep.-LLDA (SCVB-Dep.)

Scalability to large datasets or even potentially infinite data streams is an important requirement for many application contexts. Additionally to the training runtime, memory constraints may become a problem when performing Gibbs sampling over large datasets since the whole dataset has to be kept in memory. Online algorithms allow incremental updates using batches of data, making them very memory efficient. We therefore present the online version of our classifier, SCVB-Dependency, in this section. For this we develop a method similar to the stochastic collapsed variational Bayes (SCVB) method by Foulds et al. (2013) with two important differences. First, we derive variational update equations suitable to Fast-Dep.-LLDA with its additional topic level. Second, we put forward a greedy layer-wise training algorithm that is applicable in the online setting. This enables to train a classifier with only one iteration over the dataset.

The fully factorized variational distribution of Fast-Dep.-LLDA is given by

$$\begin{aligned} q\left( z,z',\theta ',\phi ,\phi '\right) = \prod _{ij} q(z_{ij}|\gamma _{ij}) \prod _{ij} q\left( z'_{ij}|\gamma '_{ij}\right) \prod _j q(\theta '_j|\tilde{\alpha }) \end{aligned}$$

(10)

for tokens i and documents j.

In the equation, we introduce an additional variational parameter $\gamma '$ for the topic assignments $z'$. However, computing the updates for $\gamma$ and $\gamma '$ separately would lead to unnecessary computational effort. We propose to instead compute an intermediate value $\lambda _{wyk}$ which corresponds to the expectation of a joint occurrence of word w, label y and topic k which can be expressed in terms of an expectation of the indicator function $\mathbb {1}$ which is one if these values occur together and otherwise zero: $\mathbb {E}[\mathbb {1}[w_n=w,y_n=y,k_n=k]]$, where n is the nth token.

According to standard variational Bayes derivations, the lower bound for the posterior is given by

$$\begin{aligned} {\mathcal {L}}(q)&=\mathbb {E}[\log (P(\theta '|\alpha )]+\mathbb {E}[\log (P(z'|\theta ')]+\mathbb {E}[\log (P(z|z',\phi ')]\\&\quad +\,\mathbb {E}[\log (P(w|z,\phi )]-{\mathcal {H}}(q) \end{aligned}$$

where ${\mathcal {H}}(q)$ denotes the entropy of the variational distribution.

The update for $\lambda _{ij}$ is now obtained by expanding the lower bound and isolating all terms containing $\lambda$,

$$\begin{aligned} {\mathcal {L}}_{[\lambda ]}(q)&=\sum _N\sum _Y\sum _{K}\lambda _{wyk}\left( \psi (\tilde{\alpha _{k}})-\psi \left( \sum _{j=1}^{K}\tilde{\alpha _{j}}\right) \right) \\&\quad +\,\sum _N\sum _Y\sum _{K}\sum _{V}\lambda _{wyk}w^v_n\log \left( \phi _{vy}\phi '_{yk}\right) \end{aligned}$$

adding Lagrange multipliers, computing the derivative with respect to $\lambda _{ij}$, and setting it to zero. This leads to the following update equation for $\lambda _{ij}$, assuming that w is the word at position i of document j.

$$\begin{aligned} \lambda _{wyk}\propto \phi _{wy}\phi '_{yk}\exp \left( \psi \left( \tilde{\alpha _{k}}\right) \right) \end{aligned}$$

(11)

If we include $\phi$ and $\phi '$ in the variational distribution, marginalize over $\theta '$, $\phi$, and $\phi '$ and only use the first term of the Taylor approximation as in Teh et al. (2006b), we arrive at the update

$$\begin{aligned} \lambda _{wyk}\propto \frac{N^{\phi }_{w_{ij},y}+\eta _{w}}{N^Z_y+\sum _w{\eta _w}}\frac{N^{\phi '}_{y_{ij}}+\eta _{y}}{N^{Z'}_k+\sum _y{\eta _y}}\left( N^{\theta '}_{jk}+\alpha \right) \end{aligned}$$

(12)

From this we can recover $\gamma _{wk}=\sum _{k'} \lambda _{wkk'}$ and $\gamma _{kk'}=\sum _{w} \lambda _{wkk'}$ by marginalization, however we do not need these variational distributions for our updates, since it is straightforward to use $\lambda$ directly. $N^Z$ is a vector storing the expected number of words for each label. $N^{\phi }$ is the expected number of tokens for words w and labels y in the whole corpus. Additionally, $N^{Z'}$ stores the expected number of tokens for each topic, $N^{\phi '}$ is the expected number of tokens for labels y and topics k, and $N^{\theta '}_j$ is the expected number of words per topic, only for document j.

The stochastic update equations are derived analogously to the ones by Foulds et al. (2013), except that we update $\phi$, $\phi '$ and $\theta '$ instead of just $\phi$ and $\theta$. We use the terminology of Foulds et al. for easier comparison and summarize the additional notation in Table 3. Updates are done for minibatches M with update percentage $\rho$. C is the number of overall tokens and $C_j$ is the number of tokens in document j.

Table 3 Additional notation for SCVB-Dep. model

For each token (the ith word in the jth document) we calculate $\lambda _{ijyk}$ for label y and topic k, where during training $\lambda$ only has to be calculated for the labels of the document and should be set to zero for all other labels.

$$\begin{aligned} \lambda _{ijyk}&:\propto&\lambda ^{W}_{ijy} \lambda ^{T}_{ijyk} \end{aligned}$$

(13)

$$\begin{aligned} \lambda ^{W}_{ijy}&:\propto&\frac{N^{\phi }_{w_{ij},y}+\eta _{w}}{N^Z_y+\sum _w{\eta _w}} \end{aligned}$$

(14)

$$\begin{aligned} \lambda ^{T}_{ijyk}&:\propto&\frac{N^{\phi '}_{y_{ij}}+\eta _{y}}{N^{Z'}_k+\sum _y{\eta _y}}\left( N^{\theta '}_{jk}+\alpha \right) \end{aligned}$$

(15)

Because we do greedy layer-wise training, we can train the two parts of the model separately (see Algorithm 2), whereas during testing we have to use the full model (see Algorithm 1). In Algorithm 2, the first layer treats every word as an input token and updates the word-label distribution based on $\lambda ^W$ (lines 11–15), whereas the second layer treats each label assignment as an input token and learns the label-topic distributions based on $\lambda ^T$ (lines 16–21). Since we want to train our model online, we cannot wait for the greedy algorithm to learn the first layer before moving on to the second layer. Therefore, we resort to initializing the input probabilities of the second layer by using the true labels. Thereby we can train both layers simultaneously while not having to view any document more than once.

The update equations using $\lambda$ and the update parameter $\rho$ for estimating $N^{\phi }$, $N^{Z}$, $N^{\phi '}$, $N^{Z'}$ and $N^{\theta '}$ are:

$$\begin{aligned} N^{\theta '}_j:= & {} \left( 1-\rho ^{\theta '}\right) N^{\theta '}_j+\rho ^{\theta '}C_j\sum _y\lambda _{ijy} \end{aligned}$$

(16)

$$\begin{aligned} N^{\phi }:= & {} \left( 1-\rho ^{\phi }\right) N^{\phi }+\rho ^{\phi }{\hat{N}}^{\phi }, \end{aligned}$$

(17)

where ${\hat{N}}^{\phi }=\frac{C}{|M|}\sum _{i,j\in M}\sum _{k}Y^{i,j,k}$ and $Y^{i,j,k}$ is a |W| times |Y| matrix with the $w_i$th row corresponding to $\sum _k\lambda _{i,j,.,k}$ and zero in all other places.

$$\begin{aligned} N^{\phi '}:=\left( 1-\rho ^{\phi '}\right) N^{\phi '}+\rho ^{\phi '}{\hat{N}}^{\phi '} \end{aligned}$$

(18)

where ${\hat{N}}^{\phi '}=\frac{C}{|M|}\lambda _{ij}$.

$$\begin{aligned} N^Z:=\left( 1-\rho ^{\phi }\right) N^{Z}+\rho ^{\phi }{\hat{N}}^Z, \end{aligned}$$

(19)

where ${\hat{N}}^Z=\frac{C}{|M|}\sum _{i,j\in M}\sum _k\lambda _{ij.k}$.

$$\begin{aligned} N^{Z'}:=\left( 1-\rho ^{\phi '}\right) N^{Z'}+\rho ^{\phi '}{\hat{N}}^{Z'}, \end{aligned}$$

(20)

where ${\hat{N}}^{Z'}=\frac{C}{|M|}\sum _{i,j\in M}\sum _y\lambda _{ijy}$.

The whole inference algorithm is given in Algorithm 1. For each document we first do zero or more burn-in passes to get a better estimate of $N^{\theta '}$ (line 5–9). We then update the estimates ${\hat{N}}^{\phi }$, ${\hat{N}}^{\phi '}$, ${\hat{N}}^{Z}$, and ${\hat{N}}^{Z'}$ for each token in the current minibatch (line 11–18). Finally, for each minibatch the global estimates $N^{\phi }$, $N^{\phi '}$, $N^{Z}$, and $N^{Z'}$ are updated (line 20–23).

To sum up, we derived a variational Bayes learning algorithm for Fast-Dep.-LLDA to use greedy layer-wise training in the online setting.

4.4 Reversed Fast-Dep.-LLDA

One problem when learning a topic model where each topic corresponds to a label is that the labels might not be a good way to represent the data. There might be very similar labels (e.g. model, models and modeling) that could be grouped together into a single topic, and there might be very broad labels that could be subdivided into several topics. To get a better representation of the data, we may use the same model with topics and labels swapped. This means each label is associated with a distribution over topics.

We can also apply our model in this context, despite the fact that now the first layer of topics cannot be trained without information from its prior since it is not supervised anymore. The second layer however, since it is the supervised level, can be trained greedily by using a uniform document-label distribution $\theta '$. Thereby we recover the well-known author-topic model during training. During testing we would have to put the dependence on the prior document-label $\theta '$ distribution back into the model.

This leads to the following update equations for label assignments $z'$ and topic assignments z during training:

$$\begin{aligned}&P\left( z=y|w,z'=k,z_{-i},z'_{-i}\right) \propto \frac{n^{w_i}_{-iy}+\beta }{n^{.}_{-iy}+|W| \beta }\left( n^{y}_{-ik}+\beta _y\right) \end{aligned}$$

(21)

$$\begin{aligned}&P\left( z'=k|z=y,z_{-i},z'_{-i}\right) \propto \frac{n^{y}_{-ik}+\beta _y}{n^{.}_{-ik}+|Y|\beta _y} \end{aligned}$$

(22)

During testing Eq. (8) has to be used instead of Eq. (22).

This model is not meant for classification, but for generating representative word clouds that are not as much dependent on the given label assignments.

4.5 Prediction

For prediction in our model, we differentiate between two prediction strategies. For both strategies, we fix the estimated matrices $\phi$ and $\phi '$ and just modify the document counts to get an estimate of $\theta '$. However, unlike in Dep.-LLDA, we do not have an explicit document-label distribution incorporated in our model, we only have the document-topic distribution $\theta '$. This is not a problem since we can simply use the conditional probabilities for z directly in our prediction. The first strategy (S1) estimates the probability of label y in document d given $z'=k$ as $\frac{1}{n^d}\sum _{w\in d}{\frac{n^{w_i}_{-iy}+\beta }{n^{.}_{-iy}+|W| \beta }\frac{n^{y}_{-ik}+\beta _y}{n^{.}_{-ik}+|Y|\beta _y}(n^{d}_{-ik}+\alpha )}$. The second strategy (S2) is more similar to the evaluation strategy of Dep.-LLDA. We estimate the posterior predictive distribution over labels as $P(z=y|\phi ',\theta ')=\sum _{t=1}^{T}\phi '_{yt}\theta '_{dt}$. We then sample the labels from a standard LLDA model with an asymmetric label prior $\alpha _y=n^d*P(z=y|\phi ',\theta ')$. This means the conditional probability for sampling of the labels as well as estimation is given by $P(z=y|rest)\propto \frac{n^{w_i}_{-iy}+\beta }{n^{.}_{-iy}+|W| \beta }(n_dy+\alpha _y)$. This evaluation strategy is more expensive since we have to calculate the asymmetric label prior $\alpha$, however, it allows to explicitly represent the document-label distribution needed for prediction.

We run ten chains for each classifier taking 100 samples from each chain to get an estimate from each chain. These estimates are averaged again over the different chains to produce the final estimate.

For Dep.-LLDA, the original publication uses an estimate of $\theta$ for the prediction. However to make the comparison fair and because we found it to deliver better results,¹ we also used an average over the conditional probability for $z=y$ (Eq. 1) in this case: $\frac{1}{n^d} \sum _{w\in d}{\frac{n^{w_i}_{-iy}+\beta }{n^{.}_{-iy}+|W| \beta }(n^{d}_{-iy}+\alpha ')}$.

In the case of the online models SCVB and SCVB-Dependency, we use a normalized version of $N^Z$ for the prediction of each document.

4.6 Computational complexity

Both methods, Dep.-LLDA as well as our Fast-Dep.-LLDA have a computational complexity of $O(|Y|+|T|)$ for one sampling step since we have to sample one of |Y| labels and one of |T| topics. For Fast-Dep.-LLDA this can be reduced to $O(j_t+k_d)$, where $j_t$ is the number of labels in topic t and $k_d$ is the number of topics in document d using more efficient sampling techniques (Li et al. 2014). For Dep.-LLDA only the sampling of topics can be sped up, leading to an improved complexity of $O(|Y|+k_d)$. Furthermore, the calculation of $\alpha '$ leads to a higher computation time of Dep.-LLDA as compared to our evaluation strategy S1 even though the complexity is not affected as long as we do not assume that the document length is much lower than the number of topics. Our second evaluation strategy S2 also involves the calculation of $\alpha$ meaning the computational complexity is equal to that of Dep.-LLDA in that case. Summing up, both methods have the same complexity, however, our method using evaluation strategy S1 is expected to be faster in practice and when more efficient sampling methods are used, our S1 method has an improved complexity.

5 Experimental results

5.1 Binary predictions

All compared classifiers produce predictions in the form of a probability distribution over labels. To be able to compare on standard multi-label classification measures such as F-measure, we need to transform them to binary predictions. The approach we take is to train a regression model on the features x that predicts the number of labels to set to true for each instance. We then round the resulting number to the nearest integer and set the most probable labels to true. The reason for this approach is that it is independent of the used classifier, meaning that we can predict the number of labels for each test instance once and use this prediction for the output of each classifier. In experiments not reported here in detail, this approach outperformed the approach with a cut-off set to an arbitrary fixed value. To train the model, we use a subset of 10,000 training documents. As a regression method we chose Lasso. Parameters were chosen via cross-validation.

5.2 Evaluation measures

We evaluate all batch classifiers on three ranking based and five binary classification measures. The ranking based measures are micro- and macro-averaged AUC and the rank one error. Micro-averaged AUC is indicative of the overall rankings of correct and incorrect labels over all instances and labels, whereas macro-averaged AUC evaluates the rankings of all instances per label and averages over the labels. The rank one loss is the error rate just for the highest ranking label.

The main binary measures are micro- and macro-averaged F-measure:

$$\begin{aligned} \text{ Micro-F1 } = 2\frac{\text{ Micro-Precision }*\text{ Micro-Recall }}{\text{ Micro-Precision }+\text{ Micro-Recall }}, \end{aligned}$$

(23)

where Micro-Precision is defined as:

$$\begin{aligned} \text{ Micro-Precision } = \frac{\sum _{y\in Y}\text{ tp }_y}{\sum _{y\in Y}(\text{ tp }_y+\text{ fp }_y)}, \end{aligned}$$

(24)

where Y is the set of all labels, $\text{ tp }_y$ are true positives for label y and $\text{ fp }_y$ are the false positives for label y. Micro-Recall is defined as:

$$\begin{aligned} \text{ Micro-Recall } = \frac{\sum _{y\in Y}\text{ tp }_y}{\sum _{y\in Y}\text{ tp }_y+\text{ fn }_y} \end{aligned}$$

(25)

The macro-averaged F-measure is defined as:

$$\begin{aligned} \text{ Macro-F1 } = \frac{1}{|Y|}\sum _{y\in Y}\frac{\text{ Precision }_y*\text{ Recall }_y}{\text{ Precision }_y+\text{ Recall }_y} \end{aligned}$$

(26)

In addition to the F-measure results, we also report the individual micro-precision and micro-recall.

Furthermore we report the common Hamming loss measure. The Hamming loss is simply the error rate over all instances and labels. In our setting with the large number of labels this is usually a low value since most labels are correctly predicted as negative.

Table 4 Number of labels, attributes, instances, cardinality and average number of tokens per document for the used datasets

5.3 Datasets

We performed the evaluation on three publicly available multi-label text datasets with a focus on large datasets with many labels. The dataset statistics are shown in Table 4. We used a fixed testset for all datasets. EUR Lex is a dataset of legal documents concerning the European Union. It is hand annotated with almost 4,000 labels. For EUR Lex (Loza Mencía and Fürnkranz 2010) the last 10% are reserved for testing. The Ohsumed dataset² is a subset of MEDLINE medical abstracts that were collected in 1987 and that have 11,220 different human-assigned MeSH descriptors. We simply used the provided abstracts and MeSH descriptors and disregarded other information such as further qualifiers or authors. We removed stop words and retained the most frequent 20,000 features. 10% of the data were separated for the testset. The Amazon dataset consists of more than one million product reviews, annotated with corresponding product categories. The original dataset is available from http://manikvarma.org/downloads/XC/XMLRepository.html under the name AmazonCat-13K. We randomly sampled 10,000 documents from the testing dataset since our evaluation methods are not feasible for larger testsets. The features were further pruned to exclude stopwords and only use the 20,000 most frequent features. Since the dataset is only provided in a processed format and the authors were not able to provide the unprocessed dataset, we took the following steps to arrive at a raw tokenized format: We normalized the document length to 100. The feature values were then rounded to the nearest integer with a minimum value of 1.

For the experiments with BR, a TF-IDF transform of the features is applied for all datasets.

5.4 Experimental setting

5.4.1 Topic modeling methods

For the batch setting we compared the original Dep.-LLDA to our Fast-Dep.-LLDA. Dep.-LLDA serves as the main baseline since it is known to consistently outperform other topic modeling methods such as LLDA. It is also closest to our model with respect to interpretability. As discussed in the related work section, most other multi-label classifiers are not able to deal with datasets of the size and the number of labels that we test with. The implementation of Dep.-LLDA uses the fast inference method and applies the heuristic of scaling $\alpha '$ according to the document length. We use 100 topics for all datasets and methods. This is the same default setting employed by Rubin et al. who reported that a higher number tended to induce redundancy in the topics. We also did not observe a performance improvement. However, we hypothesize that using nonparametric methods based on hierarchical Dirichlet processes (Teh et al. 2006a) could possibly enable the use of larger topic numbers in future work. Additionally, we use $\beta =\beta _y=0.01$, $\sum \gamma = 10$, $\sum \alpha =30$ during testing, and $\eta =100$. These values also correspond to the values used by Rubin et al. and the values for $\beta$ and $\beta _c$ are frequently used in most literature on LDA topic models. The optimization of $\beta$ is shown to have no positive effect on results in previous work (Wallach et al. 2009), however, grid search for optimal symmetric values would possibly lead to a small improvement in the batch setting. Our main emphasis is on the streaming setting and a grid search could lead to poor results if it is only done on the first batch. Fast-Dep.-LLDA uses the same values for $\beta$ and $\sum \alpha =30$.

To evaluate our online classifier, SCVB-Dependency, each classifier is first trained for 100 iterations on an initial batch of the data and then sequentially tested on the next batch before training on it using only one iteration over each batch. As a baseline we compare to the standard stochastic collapsed variational Bayes (SCVB) model by Foulds et al. (2013). The update parameter $\rho$ is determined as $\frac{s}{(\tau +t)^{\kappa }}$ for iteration t with $s=1$, $\tau =1000$ and $\kappa =0.9$ for $\rho ^{\theta '}$ and $s=10$ and $\tau =2000$ for $\rho ^{\phi }$ and $\rho ^{\phi '}$. Additionally we use default parameter values $\eta _w=\eta _y=0.01$ and $\alpha =0.1$.

5.4.2 BR(SVM)

BR is the second baseline we chose because it does not consider label dependencies and therefore allows assessing the effect of modeling dependencies. Binary Relevance learns one separate SVM for each label. The publicly available LIBLINEAR (version 1.98) is used for the SVMs, implemented in C++. The SVM parameter C is optimized in the range $[10^{-3},\ldots ,10^3]$ using 3-fold cross-validation for each label separately. The output of an SVM for each label represents the distance to the decision surface. To transform this to probability outputs, it would be necessary to apply Platt’s scaling or a similar method. Platt’s scaling involves training a logistic regression model on the output of the SVM. In our case this would mean, producing the SVM-output for the whole training set and training an additional logistic regression model for each label. Possibly, this procedure would improve the SVM results (we are not aware of any systematic study concerning this issue in multi-label classification), however, we resorted to using the distances directly since the training of BR is already very expensive without further postprocessing of the results. Previous work follows the same procedure. Nam et al. (2014) and Rubin et al. (2012) also do not mention a transformation of SVM outputs to probabilities. This is especially problematic in their evaluation, since they do not use thresholds for each instance, but use a label-based cut-off for the whole testset, i.e. they select the number of positive instances per label. For each label, outputs are generated using a sigmoid as $o_1=1/(1+\text{ exp }(-distance))$ and $o_2=1-o_1$, where distance is the distance to the decision surface. To be able to train a BR on our large datasets, we used our own Python implementation and trained the models in parallel. Note that the use of linear kernels is well supported by previous literature on text classification methods as they are not only much more efficient in training, but also have a comparable performance to nonlinear kernels in this high dimensional setting (Lewis et al. 2004).

5.4.3 FastXML

As a state-of-the-art method of comparison in extreme multi-label learning, we additionally chose FastXML by Prabhu and Varma (2014). This model is an ensemble of decision trees similar to random forests, but optimizing a different loss function leading to improved results. The C-Code is provided on the author’s website http://manikvarma.org/downloads/XC/XMLRepository.html and we used the default settings of the software.

5.4.4 PD sparse

PD Sparse is another multi-label method for extreme multi-label classification. Yen et al. (2016) propose to use a margin-maximizing loss with L1-penalty yielding an extremely sparse solution. This classifier is sublinear in the number of labels and thus applicable in even more extreme settings with millions of labels. The C-Code is available at http://manikvarma.org/downloads/XC/XMLRepository.html and default settings were used.

Table 5 Classification and ranking measures for Binary Relevance with SVMs, Dep.-LLDA, our Fast-Dep.-LLDA, and Fast-Dep.-LLDA with the more complex evaluation strategy S2

Table 6 Classification and ranking measures for Binary Relevance with SVMs, Dep.-LLDA, our Fast-Dep.-LLDA, and Fast-Dep.-LLDA with the more complex evaluation strategy S2

5.5 Results

5.5.1 Batch methods

As the results in both Tables 5 and 6 show, with regards to our method Fast-Dep.-LLDA, evaluation strategy S2 is superior to evaluation strategy S1. This shows that it is important to explicitly represent the label distributions during prediction. Table 5 shows the results for the batch methods where the final distributions were obtained by averaging the distributions from ten different chains. We can see that Fast-Dep.-LLDA has almost always the best results for micro- and macro-averaged AUC. However, BR is better on the binary classification measures. We assume that this is due to the issue discussed in Sect. 5.4.2. BR does by default not produce probabilities as outputs which might affect the ranking performance between different instances. Our binary cut-offs are determined instance-wise which means that the binary results only depend on the ranking of labels per instance. The only binary measure where BR is not best is macro-averaged F-measure, where BR is only best on the Amazon dataset, whereas the topic modeling methods are better on the other two datasets. The Amazon dataset is the largest dataset which might provide BR with enough training data to be able to predict the labels without taking dependencies into account. Macro-averaged measures are indicative for the performance on rare labels. We can therefore draw the conclusion that in cases where the number of labels is large relative to the size of the training dataset, the topic modeling methods are better at predicting rare labels.

For PD Sparse and the decision tree method FastXML we only provide the binary measures and the ranking loss since the methods do not produce probability outputs. In comparison to BR and the topic modeling methods, these two extreme multi-label methods are mostly worse. Only for the Ohsumed dataset PD Sparse is best on macro-averaged F-measure whereas FastXML is best on rank one error. While these extreme multi-label classification methods are very scalable and could easily handle even bigger label and feature sets, they are not competitive in terms of classification performance with the other medium-large-scale multi-label classifiers.

In Table 6 we compare the results of the topic modeling classifiers on only one chain and perform significance tests. Significance is tested using a t-test comparing our classification methods to the original Dep.-LLDA. Fast-Dep.-LLDA (S2) is significantly better than Dep.-LLDA on micro- and macro-averaged AUC. For the binary classification measures the results are less pronounced. Fast-Dep.-LLDA (S2) has better results on the Ohsumed dataset, but for the micro-averaged measures they are not significant. For macro-averaged F-measure, Fast-Dep.-LLDA (S2) is significantly better for the Ohsumed dataset, but worse for the other two datasets.

Fig. 8

Performance of our online classifier SCVB-Dependency compared to SCVB (micro-/macro-averaged AUC). An initial batch is trained with 1000 instances. Classifiers are then updated with the next batch size instances and tested on the following batch size instances. Results are averaged over ten runs with random orderings of the datasets. a, d EUR Lex dataset, b, e Ohsumed dataset, c, f Amazon dataset

5.5.2 Online methods

Figure 8 shows the performance of the online methods for micro- and macro-averaged AUC. Each classifier is first trained on an initial batch of instances for 100 iterations and then subsequently tested on the next batch and updated on the next batch using one iteration. The results are averaged over ten runs. The Fast-Dependency-SCVB method outperforms the plain SCVB on all datasets and both measures. This shows that our method is able to learn the dependencies in the online setting.

5.5.3 Runtime

All experiments are performed on an Intel Core i7-4770K CPU 3.50 GHz $\times$ 8. All methods were implemented in Java.

The training runtime of the batch vs. the online version of our method is plotted in Fig. 9 against micro-averaged AUC. On the EUR Lex and Amazon datasets, the online method converges much faster than the batch method and is able to provide results long before the batch method has even finished the first iteration. On the Ohsumed dataset, the batch method converges faster. This is probably the case because the Ohsumed dataset has large feature and label sets relative to the training dataset size. Therefore the overhead introduced by the batch updates of the online method slows the model down. With a smaller feature set and/or a larger training dataset, the online method would also be faster in this case. To sum up, the online method is faster to train and converges earlier than the batch method given a large enough training dataset.

Fig. 9

Runtime comparison: training runtime against testset performance in terms of micro-averaged AUC (the test dataset is fixed). Compared are our online method SCVB-Dep. and our batch method Fast-Dep.-LLDA. For the batch method, samples are only taken from a single chain which is why the performance of the online method may be better after convergence. a EUR Lex dataset, b Ohsumed dataset, c Amazon dataset

5.5.4 Reversed Fast-Dep.-LLDA

For the reversed Fast-Dep.-LLDA model described in Sect. 4, three topics after training on the Ohsumed dataset with 100 topics are shown in Fig. 10. For each topic we show the frequent labels as a label cloud and the frequent words as a word cloud. As we can see, many labels are strongly related and the topic clouds might in some cases be more useful descriptions of the dataset content than the label clouds that result from non-reversed Fast-Dep.-LLDA.

Fig. 10

Label and word clouds for Fast-Dep.-LLDA-Reversed on the Ohsumed dataset. The 30 most frequent words and 10 most frequent labels are shown for three exemplary topics. a Labels for topic 1, b words for topic 1, c labels for topic 3, d words for topic 3, e labels for topic 6, f words for topic 6

6 Discussion

We introduced a batch method based on Gibbs sampling and an online method based on variational Bayes. Gibbs sampling generally has the advantage of being unbiased, variational Bayes is faster to converge but biased. Online variational Bayes has been shown to converge to a local optimum of the variational Bayes objective function (Hoffman et al. 2010). For Gibbs sampling we need many iterations for convergence. In practice, however, it might in some cases be feasible to employ the Gibbs sampling method in an online setting, meaning that we process each instance only once (Canini et al. 2009). Since the labels are predetermined during training, it might not be necessary to perform more than one iteration over the training dataset. However, there is no theoretical guarantee that this is the case. The higher the label cardinality of a dataset, the longer it generally takes for the Gibbs sampler to converge. Therefore, our online method is preferable in true online settings where a stream of data arrives and it is not possible to store all arriving data.

We observed very different outcomes of the ranking performance as compared to the classification performance of our method. While the ranking performance is mostly better than that of Dep.-LLDA and the ranking performance of all topic modeling methods is much better than that of BR with SVMs, the results are different for the binary classification measures. Here, BR(SVM) clearly emerges as the overall best performing method, except on macro-averaged F-measure. The performance on macro-averaged F-measure is an indication for the good performance on rare labels due to the learned label dependencies. We suspect that the ranking performance of BR(SVM) could be further improved by postprocessing its prediction outputs. Nevertheless, BR(SVM) is a far more complex method in terms of training runtime. Despite parallelization, the training of BR for the Amazon dataset took several days, whereas the training runtime of the topic modeling methods is a matter of several minutes to a few hours on a single core. BR is therefore more expensive in terms of runtime, but only preferable if the classification performance is the only important factor and computational resources are not taken into account. In summary, the topic modeling methods are more scalable and efficient, ranking performance seems to be better without requiring expensive postprocessing, and most importantly, they may be used in the online setting where real-time analyses are required.

7 Conclusion

We identified the main success factor of Dep.-LLDA, namely the separate training of topic and label level. Based on this, we developed an improved version of the multi-label topic model Dep.-LLDA, called Fast-Dep.-LLDA, which uses a greedy layer-wise training procedure. We showed that Fast-Dep.-LLDA has theoretical as well as practical advantages. The sampling procedure is consistent with the defined model and heuristics are avoided. In terms of ranking performance, our method is superior to BR(SVM). While the label ranking performance is superior to the existing Dep.-LLDA model, the binary classification performance is still competitive. Overall our classifier is easier to implement than Dep.-LLDA, able to handle thousands of labels as opposed to BR and most other multi-label methods, and therefore much more appealing for practical applications. Additionally it can easily be modified so it may be used for analyzing label dependencies, and generalizes the well-known author-topic model (Rosen-Zvi et al. 2004).

We also introduced an online classifier called SCVB-Dep. that is based on the same graphical model as Fast-Dep.-LLDA, but is trained in an online fashion. We showed that it has a better performance than the non-dependency SCVB and that it converges faster than Fast-Dep.-LLDA during training on large datasets.

In future work we would like to extend the presented online model by allowing it to add new labels over time.