Learning safe multi-label prediction for weakly labeled data

Abstract

In this paper we study multi-label learning with weakly labeled data, i.e., labels of training examples are incomplete, which commonly occurs in real applications, e.g., image classification, document categorization. This setting includes, e.g., (i) semi-supervised multi-label learning where completely labeled examples are partially known; (ii) weak label learning where relevant labels of examples are partially known; (iii) extended weak label learning where relevant and irrelevant labels of examples are partially known. Previous studies often expect that the learning method with the use of weakly labeled data will improve the performance, as more data are employed. This, however, is not always the cases in reality, i.e., weakly labeled data may sometimes degenerate the learning performance. It is desirable to learn safe multi-label prediction that will not hurt performance when weakly labeled data is involved in the learning procedure. In this work we optimize multi-label evaluation metrics ($\hbox {F}_1$ score and Top-k precision) given that the ground-truth label assignment is realized by a convex combination of base multi-label learners. To cope with the infinite number of possible ground-truth label assignments, cutting-plane strategy is adopted to iteratively generate the most helpful label assignments. The whole optimization is cast as a series of simple linear programs in an efficient manner. Extensive experiments on three weakly labeled learning tasks, namely, (i) semi-supervised multi-label learning; (ii) weak label learning and (iii) extended weak label learning, clearly show that our proposal improves the safeness of using weakly labeled data compared with many state-of-the-art methods.

1 Introduction

In many real applications, learning objects are associated with multiple labels. For example, in image classification (Carneiro et al. 2007), one image can be associated with many concept labels such as ‘sky’, ‘cloud’, ‘flower’, etc; in document categorization (Srivastava and Zane-Ulman 2005), one document could be related to multiple topics such as ‘sport’, ‘football’, ‘lottery’, etc. Multi-label learning (Zhang and Zhou 2014) is now one hot research area in dealing with learning examples related to multiple labels. Due to its wide suitability, multi-label learning techniques have been adopted for many applications, and a number of multi-label learning algorithms have been developed (Tsoumakas et al. 2009; Zhang and Zhou 2014).

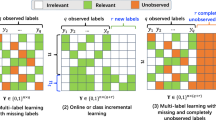
Although multi-label representation provides a better characterization than single-label one, in real applications the acquisition of labels suffers from various difficulties, and weakly labeled data, i.e., labels of training examples are incomplete, commonly occurs. For example, human labelers may only give labels for a few training examples. In this case, completely labeled examples are partially available and many training examples are unlabeled, which is realized as semi-supervised multi-label learning problem (Liu et al. 2006; Kong et al. 2013); human labelers may only give partial relevant labels for training examples. In this case, relevant labels of training examples are partially known and many relevant labels are missing, which is realized as weak label learning problem (Sun et al. 2010); human labelers may only give partial relevant and irrelevant labels for training examples. In this case, relevant and irrelevant labels of training examples are partially known, we refer it to extended weak label learning problem. Figure 1 illustrates three weakly label assignments for multi-label training data. Over the past decade, multi-label learning with weakly labeled data attracts increasing attentions and a large number of algorithms have been presented  (Liu et al. 2006; Sun et al. 2010; Chen et al. 2008; Kong et al. 2013; Wang et al. 2013; Yu et al. 2014; Zhao and Guo 2015).

In previous studies, it is often expected that multi-label learning methods with the use of weakly labeled data are better than counterpart approaches, i.e., supervised multi-label learning methods using only labeled data, as more data are employed. This, however, is not always the cases in reality. As reported in quite many empirical studies  (Chen et al. 2008; Wang et al. 2013; Zhao and Guo 2015), using more weakly labeled data may sometimes degenerate learning performance. This hinders multi-label learning to play roles in more applications. It is important to have safe multi-label learning methods which could always improve the learning performance with weakly labeled data, and in the worst case scenario, they will not degenerate performance. Figure 2 illustrates the motivation of the paper.

To overcome this issue, in this work we propose SafeML (SAFE Multi-Label prediction for weakly labeled data). It directly optimizes multi-label evaluation metrics ($\hbox {F}_1$ score and Top-k precision) via formulating a distribution of ground-truth label assignments. Specifically, we assume that ground-truth label assignments are realized by a convex combination of multiple basic multi-label learners, inspired by Li et al. (2017). To cope with the infinite number of possible ground-truth label assignments in optimization, cutting-plane strategy is adopted, which iteratively generates the most helpful label assignments. The optimization is then cast as a series of simple linear programs in an efficient manner. Extensive experiments on three weakly labeled tasks, namely, i) semi-supervised multi-label learning; ii) weak label learning and iii) extended weak label learning, show that our proposal clearly improves the safeness for the use of weakly labeled data, in comparison to many state-of-the-art methods.

Fig. 1

Illustration for weakly labeled data. $+\,1$ and $-\,1$ represent relevant and irrelevant labels. Red cells represent missing labels. In this paper three kinds of weakly labeled data are considered, namely, semi-supervised multi-label, weak label and extended weak label learning (Color figure online)

Fig. 2

Motivation of the paper. In many cases, traditional multi-label learning algorithms using weakly labeled data may degenerate the learning performance, which is not in line with our expectation

The rest of the paper is organized as follows. We first introduce some related works and then present the proposed method. This is then followed by extensive experimental results, and finally we give conclusive remarks.

2 Related work

This work is related to two branches of studies. The first one is multi-label learning approaches for weakly labeled data. As for semi-supervised multi-label learning problem, one early work is proposed by Liu et al. (2006). They assumed that the similarity in the label space is closely related to that in the feature space, and thus employed the similarity in feature space to guide the learning of missing label assignments, which leads to a constrained nonnegative matrix factorization (CNMF) optimization. Later, Chen et al. (2008), inspired by the idea of label propagation, inferred the label assignments for unlabeled data via two graphs on instance-level and label-level respectively. Similarly, Wang et al. (2013) proposed to propagate from labeled data to unlabeled data via a dynamic graph. Zhao and Guo (2015) aimed to improve multi-label prediction performance by integrating label correlation and multi-label prediction in a mutually beneficial manner.

As for weak label learning problem, there are some approaches. One early work is proposed by Sun et al. (2010). They employed label propagation idea to learn missing label assignments and controlled the quality of learned relevant labels through sparsity regularizer. Bucak et al. (2011) formulated the problem via standard statistical learning framework and introduced group lasso loss function that enforced the learned relevant labels to be sparse. Chen et al. (2013) first attempted to reconstruct the (unknown) complete label set from a few label assignments, and then learned a mapping from the input features to the reconstructed label set. Yu et al. (2014) first initialized the label assignments via training model on the labels observed and then performed label completion based on visual similarity and label co-occurrence of learning objects (Wu et al. 2013; Zhu et al. 2010).

As for extended weak label learning problem, to our best knowledge, it has not been studied yet and this paper is the first work on this new setting. Generally, previous multi-label learning methods on weakly labeled data typically work on improving the performance based on some assumptions/conditions, no study has been proposed on using weakly labeled data safely.

The second branch of studies is safe machine learning techniques for weakly labeled data, which are now generally focused on semi-supervised learning scenario. S4VM (Safe Semi-Supervised SVM) (Li and Zhou 2015) is one early work to build safe semi-supervised SVMs. They optimized the worst-case performance gain given a set of candidate low-density separators, showing that the proposed S4VM is provably safe given that low-density assumption (Chapelle et al. 2006) holds. UMVP (Li et al. 2016) concerns to build a generic safe SSC framework for variants of performance measures, e.g., AUC, $F_1$ score, Top-k precision.  Krijthe and Loog (2015) developed a robust semi-supervised classifier, which learns a projection of a supervised least square classifier from all possible semi-supervised least square classifiers. Most recently, Li et al. (2017) explicitly considers to maximize the performance gain and learns a safe prediction from multiple semi-supervised regressors, which is not worse than a direct supervised learner with only labeled data. However, all these works focus on binary classification or regression cases, which are not sufficient to cope with multi-label learning problems (will be verified in our empirical studies), as they fail to take rich label correlations into account.

3 Proposed SafeML method

In this section, we first present some backgrounds of multi-label learning, including problem notations and popular evaluation metrics for multi-label learning. We then present problem formulation for safe multi-label learning with weakly labeled data, followed by its optimization and analysis.

3.1 Background

Notation In traditional supervised multi-label learning, the training data set is represented as $\{(\mathbf{x }_{1}, \mathbf{y }_{1}), \ldots , (\mathbf{x }_{N}, \mathbf{y }_{N})\}$, where $\mathbf{x }_{i} \in \mathbb {R}^{d}$ is the feature vector of the i-th instance, and $\mathbf{y }_{i} \in \{-1, 1\}^{L}$ is the corresponding label vector. N and L are the number of instances and labels, respectively. The feature matrix is denoted as $\mathbf{X }= [\mathbf{x }_{1}; \ldots ; \mathbf{x }_{N}] \in \mathbb {R}^{N\times d}$ and the label matrix $\mathbf{Y }= [\mathbf{y }_{1}; \ldots ; \mathbf{y }_{N}] \in \{-1, 1\}^{N \times L}$. If instance $\mathbf{x }_{i}$ is associated to the j-th label, then $\mathbf{Y }_{ij} = 1$; otherwise, $\mathbf{Y }_{ij} = -1$. Given $\mathbf{X }$ and $\mathbf{Y }$, the goal of multi-label learning is to learn a hypothesis $f : \mathbb {R}^{d} \rightarrow \{-1, 1\}^{L}$ that accurately predicts the label vector for a given instance.

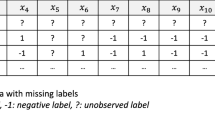
However, when weakly labeled data occurs, the label assignments in $\mathbf{Y }$ is not complete and some parts of the label assignments in $\mathbf{Y }$ are missing. In this case, what we have is an incomplete label matrix $\bar{\mathbf{Y }} \in \{-1,0,+1\}^{N \times L}$ where ‘0’ indicates the cases that the corresponding label assignments are missing.

As previously mentioned, our goal in the paper is to derive safe multi-label prediction for weakly labeled data. Specifically, given $\mathbf{Y }_0$ be the predictive label matrix based on direct supervised multi-label learning algorithms, e.g., binary relevance (Read et al. 2011), we would like to learn a safe multi-label prediction ${\hat{\mathbf{Y }}}$ from $\{\mathbf{X },\bar{\mathbf{Y }}\}$ such that ${\hat{\mathbf{Y }}}$ is often better than $\mathbf{Y }_0$ w.r.t. multi-label evaluation metrics. All the notations and their meanings are summarised in Table 1. In the following, we introduce two popular multi-label evaluation metrics.

Table 1 Summary of notation

Multi-label evaluation metrics The first one is $F_1$ score. $F_{1}$ score is a widely used evaluation for multi-label learning, which trades off precision and recall (Zhang and Zhou 2014). It takes both precision and recall into consideration with equal importance. Traditional $F_1$ score is computed for binary classification problem. When $F_1$ meets multi-label learning, it can be obtained in the following two modes.

• $Macro F_{1}$ :

  $$\begin{aligned} MacroF_{1} = \frac{1}{L}\displaystyle \sum _{j = 1}^{L}F_{1}\left( TP_{j}, FP_{j}, TN_{j}, FN_{j}\right) \end{aligned}$$

  (1)

• $MicroF_{1}$ :

  $$\begin{aligned} MicroF_{1} = F_{1}\left( \displaystyle \sum _{j = 1}^{L}TP_{j}, \displaystyle \sum _{j = 1}^{L}FP_{j}, \displaystyle \sum _{j = 1}^{L}TN_{j}, \displaystyle \sum _{j = 1}^{L}FN_{j}\right) \end{aligned}$$

  (2)

where $TP_{j}, FP_{j}, TN_{j}, FN_{j}$ represent the number of true positive, false positive, true negative, and false negative test examples with respect to label assignments of the j-th label, and

$$\begin{aligned} F_{1}(TP, FP, TN, FN) = \frac{2 TP}{2 TP + FN + FP}. \end{aligned}$$

As can be seen, $Macro F_{1}$ characterizes the average of $F_1$ scores over all the labels, while $Micro F_{1}$ characterizes the $F_1$ score w.r.t. the sum of TP, FP, TN, FN over all the labels. They both characterize the tradeoff between precision and recall, from different aspects.

The second one is Top-k precision. Top-k precision is also popularly used in multi-label learning applications (Zhang and Zhou 2014), especially for those in information retrieval or search areas. In Top-k precision, only a few top predictions of an instance will be considered. For each instance $\mathbf{x }_i$, the Top-k precision is defined for a predicted score vector $\hat{\mathbf{y }}_i \in \mathcal {R}^{L}$ and ground truth label vector $\mathbf{y }_i \in \{-1, 1\}^{L}$ as

$$\begin{aligned} Pre@k(\mathbf{y }_i, \hat{\mathbf{y }}_i) = \frac{1}{k}\displaystyle \sum _{l \in \text {rank}_{k}(\hat{\mathbf{y }}_i)}(\mathbf{y }_{i,l}+1)/2 \end{aligned}$$

(3)

where $\text {rank}_{k}(\hat{\mathbf{y }}_i)$ returns the indices of k largest value in $\hat{\mathbf{y }}_i$ ranked in descending order. Therefore, the Top-k precision for a set of training instances is derived as

$$\begin{aligned} Pre@k(\mathbf{Y }, {\hat{\mathbf{Y }}}) = \frac{1}{N}\sum _{i=1}^{N}\frac{1}{k}\displaystyle \sum _{l \in \text {rank}_{k}(\hat{\mathbf{y }}_i)}(\mathbf{y }_{i,l}+1)/2 \end{aligned}$$

(4)

3.2 Problem formulation

We now describe our prediction problem, and formulate it as a zero-sum game between two players: a predictor and an adversary which is similar to the method mentioned in Balsubramani and Freund (2015). In this game, the predictor is the first player, who plays ${\hat{\mathbf{Y }}}$, a label matrix for training instances $\{\mathbf{x }_i\}_{i = 1}^{N}$. The adversary then plays $\mathbf{Y }$, setting the ground-truth label matrix $\mathbf{Y }\in \{-1, 1\}^{N \times L}$ under the constraints that $\mathbf{Y }$ could be reconstructed by a set of base learners. The predictor’s goal is to maximize (and the adversary is to minimize) the expected learning performance on the test data. The SafeML method formulates this as the following maximin optimization framework:

$$\begin{aligned} \max \limits _{{\hat{\mathbf{Y }}}} \min \limits _{\mathbf{Y }\in \varOmega }&\;\; perf ({\hat{\mathbf{Y }}}, \mathbf{Y }) \nonumber \\ \text{ s.t. }&\;\; \varOmega = \Big \{\mathbf{Y }\Big | \mathbf{Y }= \sum _{i=1}^{b}v_i\mathbf{P }_i \Big \} \end{aligned}$$

(5)

where perf represents the target performance measure (e.g., $F_{1}$ score, Top-k precision) and $\{\mathbf{P }_1, \ldots , \mathbf{P }_b\}$ are pseudo label matrices generated by base learners, $\mathbf{v }= [v_1, \ldots , v_b]$ captures the relative importance of the b base learners. Without loss of generality, we assume that $\mathbf{v }$ is in the simplex $\mathcal {M} = \{\mathbf{v }\Big | \sum _{i=1}^{b}v_i = 1, v_i \ge 0\}$. Equation (5) leads to robust and accurate multi-label predictions, as it maximizes the learning performance w.r.t. ground-truth label assignment, meanwhile considers the risk that ground-truth label matrix is uncertain and from a distribution. In the sequel we present the optimization of Eq. (5) w.r.t. multi-label evaluation metrics, i.e., $F_1$ score and Top-k precision.

3.3 Optimize Eq. (5) with $F_1$ Score

When $F_1$ score is considered, given $\mathbf{Y }$ and ${\hat{\mathbf{Y }}}$, we have

$$\begin{aligned} \sum _{j = 1}^{L}TP_{j}= & {} \sum _{j = 1}^{L}\sum _{i = 1}^{N} \mathbb {I}(\mathbf{Y }_{i,j}=1 \wedge {\hat{\mathbf{Y }}}_{i,j}=1) \end{aligned}$$

(6)

$$\begin{aligned} \sum _{j = 1}^{L}FP_{j}= & {} \sum _{j = 1}^{L}\sum _{i = 1}^{N} \mathbb {I}(\mathbf{Y }_{i,j}\ne 1 \wedge {\hat{\mathbf{Y }}}_{i,j}=1) \end{aligned}$$

(7)

$$\begin{aligned} \sum _{j = 1}^{L}TN_{j}= & {} \sum _{j = 1}^{L}\sum _{i = 1}^{N} \mathbb {I}(\mathbf{Y }_{i,j}\ne 1 \wedge {\hat{\mathbf{Y }}}_{i,j}\ne 1) \end{aligned}$$

(8)

$$\begin{aligned} \sum _{j = 1}^{L}FN_{j}= & {} \sum _{j = 1}^{L}\sum _{i = 1}^{N} \mathbb {I}(\mathbf{Y }_{i,j}=1 \wedge {\hat{\mathbf{Y }}}_{i,j}\ne 1) \end{aligned}$$

(9)

Equation (6) shows that $\sum _{j = 1}^{L}TP_{j}$ equals to $\text {tr}\left( (\frac{{\hat{\mathbf{Y }}} + 1}{2})^{\top }(\frac{\mathbf{Y }+ 1}{2})\right)$. From Eqs. (6, 7, 9), we notice that $2TP + FN + FP$ is equal to the number of $+1$ in $\mathbf{Y }$ and ${\hat{\mathbf{Y }}}$. Thus Eq. (5) can be rewritten as following:

$$\begin{aligned} \max \limits _{{\hat{\mathbf{Y }}}} \min \limits _{\mathbf{Y }\in \varOmega } \;\; \;\;\; \frac{\text {tr}\left( \left( \frac{{\hat{\mathbf{Y }}} + 1}{2}\right) ^{\top }\left( \frac{\mathbf{Y }+ 1}{2}\right) \right) }{\sum _{i,j}\mathbb {I}(\mathbf{Y }_{i,j}=1) + \sum _{i,j}\mathbb {I}({\hat{\mathbf{Y }}}_{i,j}=1)} \end{aligned}$$

(10)

where $\mathbb {I}(\cdot )$ is the indicator function that returns 1 when the argument holds and 0 otherwise. $\sum _{i,j}\mathbb {I}(\mathbf{Y }_{i,j}=1)$ is the number of $+1$ in $\mathbf{Y }$ and $\sum _{i,j}\mathbb {I}({\hat{\mathbf{Y }}}_{i,j}=1)$ is the number of $+1$ in ${\hat{\mathbf{Y }}}$.

To simplify this problem, we consider that the ratio of relevant labels for ground-truth label assignments are approximately closely related to a constant, i.e., $\Big |\sum _{i,j}\mathbb {I}({\mathbf{Y }}_{i,j} =1) - \gamma _0\Big | \le \epsilon$ and we set $\gamma _{0}$ according to the average number of $+1$ on training data. Therefore, the denominator of the object function in Eq. (10) can be approximated as a constant and thus Eq. (10) can be written as

$$\begin{aligned} \max \limits _{{\hat{\mathbf{Y }}}} \min \limits _{\mathbf{Y }\in \varOmega }&\;\; \text {tr}\left( \left( \frac{{\hat{\mathbf{Y }}} + 1}{2}\right) ^{\top }\left( \frac{\mathbf{Y }+ 1}{2}\right) \right) \nonumber \\ \text{ s.t. }&\;\; \Big |\sum _{i,j}\mathbb {I}({\mathbf{Y }}_{i,j} =1) - \gamma _0\Big | \le \epsilon , i = 1\ldots N, \;j = 1\ldots L \nonumber \\&\;\; \Big |\sum _{i,j}\mathbb {I}({{\hat{\mathbf{Y }}}}_{i,j} =1) - \gamma _0\Big | \le \epsilon , i = 1\ldots N, \;j = 1\ldots L \end{aligned}$$

(11)

Consequently, Eq. (11) can be rewritten as the following version:

$$\begin{aligned} \max \limits _{{\hat{\mathbf{Y }}}, \theta }&\;\; \theta \nonumber \\ \text {s.t.}&\;\; \theta \le \text {tr}\left( \left( \frac{{\hat{\mathbf{Y }}} + 1}{2}\right) ^{\top }\left( \frac{\mathbf{Y }+ 1}{2}\right) \right) , \forall \; {\mathbf{Y }} \in \varOmega \nonumber \\&\;\;\Big |\sum _{i,j}\mathbb {I}({\mathbf{Y }}_{i,j} =1) - \gamma _0\Big | \le \epsilon , \; i = 1\ldots N, \; j = 1\ldots L \nonumber \\&\;\;\Big |\sum _{i,j}\mathbb {I}({{\hat{\mathbf{Y }}}}_{i,j} =1) - \gamma _0\Big | \le \epsilon , \; i = 1\ldots N, \; j = 1\ldots L \end{aligned}$$

(12)

Note that there can be an exponential number of constraints in Eq. (12), and so a direct optimization is computationally intractable. Hence we employ the cutting-plane algorithm to solve this problem. Instead of using all the constraints in $\varOmega$ to construct the optimization problem in Eq. (12), we only use an active set of constraints, which contains a limited number of constraints in $\varOmega$. Cutting-plane algorithm iteratively adds a cutting plane to shrink the feasible region. Specifically, let ${\mathcal {C}}$ be an active constraint set. With a fixed ${\hat{\mathbf{Y }}}$, the cutting-plane algorithm needs to find the most violated constraint for the current ${\hat{\mathbf{Y }}}$ by solving

$$\begin{aligned} {\mathbf{Y }} _{\text {new}}= \mathop {\arg \min }\limits _{{\mathbf{Y }}\in \varOmega }\;\; \text {tr}\left( \left( \frac{{\hat{\mathbf{Y }}} + 1}{2}\right) ^{\top }\left( \frac{\mathbf{Y }+ 1}{2}\right) \right) , \;\; \text{ s.t. } \;\; \Big |\sum _{i,j}\mathbb {I}({{\mathbf{Y }}}_{i,j} =1) - \gamma _0\Big | \le \epsilon \end{aligned}$$

(13)

and add ${\mathbf{Y }}_{\text {new}}$ to the active constraint set $\mathcal {C}$. To simplify this equation, we construct vector ${\varvec{\mathbf{z }}}_{1 \times b}$, where $\mathbf{z }_i = \mathrm {tr}(\mathbf{P }_i^{\top } \frac{{\hat{\mathbf{Y }}} + 1}{2})$ and then $\text {tr}\left( (\frac{{\hat{\mathbf{Y }}} + 1}{2})^{\top }(\frac{\mathbf{Y }+ 1}{2})\right)$ equals to ${\varvec{\mathbf{v }}}{\varvec{\mathbf{z }^{\top }}}$. Similarly, construct matrix ${\varvec{\bar{\mathbf{Z }}}}_{b \times N}$, where $\bar{\mathbf{Z }}_i = (\mathbf{P }_i{\varvec{1}}_{L \times 1})^{\top }$ and ${\varvec{1}}_{L\times 1}$ is a column vector with all L values set to be 1, then ${\varvec{\mathbf{v }}}{\varvec{\bar{\mathbf{Z }}}}{\varvec{1}}_{N \times 1}$ equals to the number of $+1$ in $\mathbf{Y }$. Hence, the problem can be rewritten as

$$\begin{aligned} \min \limits _{\mathbf{v }\in \mathcal {M}}&\;\; \mathbf{v }\mathbf{z }^{\top }\nonumber \\ \text{ s.t. }&\;\; \Big | \mathbf{v }\bar{\mathbf{Z }}{\varvec{1}}_{N \times 1} - \gamma _0\Big | \le \epsilon \end{aligned}$$

(14)

Equation (14) is a simple linear programming that is readily to solve globally and efficiently. Given active constraint set $\mathcal {C}$, which is a subset of $\varOmega$, we can replace the $\varOmega$ in Eq. (12) with $\mathcal {C}$ and obtain

$$\begin{aligned} \max \limits _{{\hat{\mathbf{Y }}}, \theta }&\;\; \theta \nonumber \\ \text{ s.t. }&\;\; \theta \le \text {tr}\left( \left( \frac{{\hat{\mathbf{Y }}} + 1}{2}\right) ^{\top }\left( \frac{\mathbf{Y }+ 1}{2}\right) \right) , \;\; \forall \;\mathbf{Y }\in \mathcal {C}\nonumber \\&\;\; \Big |\sum _{i,j}\mathbb {I}({\hat{\mathbf{Y }}}_{i,j} =1) - \gamma _0\Big | \le \epsilon , \; i = 1\ldots N, \; j = 1\ldots L \end{aligned}$$

(15)

Both the objective function and constraints in Eq. (15) are linear in $\mathbf{Y }$ and $\theta$. Hence, we can solve the Eq. (15) with a linear programming efficiently.

Algorithm 1 summarizes the pseudo code of the cutting plane algorithm. In most cases of our experiment, the algorithm converged within a maximum number of iterations (100 iterations in our experiments). The update of $\mathbf{Y }$ and ${\hat{\mathbf{Y }}}$ [i.e., Eqs. (14) and (15)] are solved by a convex and simple linear programming problem, Eq. (12) is then addressed efficiently.

3.4 Optimize Eq. (5) with top-k precision

According to Eq. (4), given $\mathbf{Y }$ and ${\hat{\mathbf{Y }}}$, Top-k precision can be formulated as

$$\begin{aligned} Pre@k(\mathbf{Y },{\hat{\mathbf{Y }}})=\frac{1}{Nk}\sum _{i=1}^{N}\sum _{j=1}^{L}\mathbb {I}({\mathbf{Y }}_{ij}=1)\mathbb {I}\left( \pi _{j}^{{\hat{\mathbf{Y }}}_i}>L-k\right) \end{aligned}$$

(16)

where $\pi ^{{\hat{\mathbf{Y }}}_i}$ is the ranking vector of ${\hat{\mathbf{Y }}}_i$, where $\pi _p^{{\hat{\mathbf{Y }}}_i} > \pi _q^{{\hat{\mathbf{Y }}}_i}$ if ${\hat{\mathbf{Y }}}_{ip} > {\hat{\mathbf{Y }}}_{iq}$(with ties broken arbitrarily). Similarly, considering that the ratio of relevant labels for ground-truth label assignments are approximately closely related to a constant, i.e., $\Big |\sum _{i,j}\mathbb {I}({\mathbf{Y }}_{i,j} =1) - \gamma _0\Big | \le \epsilon$ and each instance is constrained to be associated with exactly k positive labels, then the optimization objective becomes

$$\begin{aligned} \max \limits _{{\hat{\mathbf{Y }}}} \min \limits _{\mathbf{Y }\in \varOmega }&\;\; Pre@k(\mathbf{Y },{\hat{\mathbf{Y }}}) \nonumber \\ \text{ s.t. }&\;\;\Big |\sum _{i,j}\mathbb {I}({\mathbf{Y }}_{i,j} =1) - \gamma _0\Big | \le \epsilon , \; i = 1\ldots N, \; j = 1\ldots L \nonumber \\&\;\;\sum _{j}\mathbb {I}({{\hat{\mathbf{Y }}}}_{i,j} =1) = k, \; i = 1\ldots N \end{aligned}$$

(17)

Equation (17) can be rewritten as

$$\begin{aligned} \max \limits _{{\hat{\mathbf{Y }}}, \theta }&\;\; \theta \nonumber \\ \text {s.t.}&\;\; \theta \le Pre@k(\mathbf{Y },{\hat{\mathbf{Y }}}), \forall \; {\mathbf{Y }} \in \varOmega \nonumber \\&\;\;\Big |\sum _{i,j}\mathbb {I}({\mathbf{Y }}_{i,j} =1) - \gamma _0\Big | \le \epsilon , \; i = 1\ldots N, \; j = 1\ldots L \nonumber \\&\;\;\sum _{j}\mathbb {I}({{\hat{\mathbf{Y }}}}_{i,j} =1) = k, \; i = 1\ldots N \end{aligned}$$

(18)

Instead of using all the constraints in $\varOmega$ to construct the optimization problem in Eq. (18), we only use an active set of constraints, which contains a limited number of constraints in $\varOmega$. The proposed cutting-plane algorithm iteratively adds a cutting plane to shrink the feasible region. Specifically, let ${\mathcal {C}}$ be an active constraint set. With a fixed ${\hat{\mathbf{Y }}}$, the cutting-plane algorithm needs to find the most violated constraint by solving

$$\begin{aligned} {\mathbf{Y }} _{\text {new}}= \mathop {\arg \min }\limits _{{\mathbf{Y }}\in \varOmega } \;\; Pre@k(\mathbf{Y }, {\hat{\mathbf{Y }}}), \;\; \text{ s.t. } \;\; \Big |\sum _{i,j}\mathbb {I}({{\mathbf{Y }}}_{i,j} =1) - \gamma _0\Big | \le \epsilon \end{aligned}$$

(19)

It can be proved that the value of $Pre@k(\mathbf{Y },{\hat{\mathbf{Y }}})$ equals to $\text {tr}\left( (\frac{{\hat{\mathbf{Y }}} + 1}{2})^{\top }(\frac{\mathbf{Y }+ 1}{2})\right)$ (Li et al. 2016). Hence, Eq. (19) can be transformed into

$$\begin{aligned} {\mathbf{Y }} _{\text {new}}= \mathop {\arg \min }\limits _{{\mathbf{Y }}\in \varOmega } \;\;\text {tr}\left( \left( \frac{{\hat{\mathbf{Y }}} + 1}{2}\right) ^{\top }\left( \frac{\mathbf{Y }+ 1}{2}\right) \right) , \;\; \text{ s.t. } \;\; \Big |\sum _{i,j}\mathbb {I}({{\mathbf{Y }}}_{i,j} =1) - \gamma _0\Big | \le \epsilon \end{aligned}$$

(20)

Similar to the case in $F_1$ score, the optimization problem can be rewritten as following:

$$\begin{aligned} \min \limits _{\mathbf{v }\in \mathcal {M}}&\;\; \mathbf{v }\mathbf{z }^{\top }\nonumber \\ \text{ s.t. }&\;\; \Big | \mathbf{v }\bar{\mathbf{Z }}{\varvec{1}}_{N \times 1} - \gamma _0\Big | \le \epsilon \end{aligned}$$

(21)

Equation (21) is a simple linear programming that is readily to solve globally and efficiently. Given an active constraints set $\mathcal {C}$, which is a subset of $\varOmega$, we can replace the $\varOmega$ in Eq. (18) with $\mathcal {C}$ and obtain

$$\begin{aligned} \max \limits _{{\hat{\mathbf{Y }}}, \theta }&\;\; \theta \nonumber \\ \text{ s.t. }&\;\; \theta \le \text {tr}\left( \left( \frac{{\hat{\mathbf{Y }}} + 1}{2}\right) ^{\top }\left( \frac{\mathbf{Y }+ 1}{2}\right) \right) , \;\; \forall \;\mathbf{Y }\in \mathcal {C}\nonumber \\&\;\; \Big |\sum _{i,j}\mathbb {I}({\hat{\mathbf{Y }}}_{i,j} =1) - \gamma _0\Big | \le \epsilon , \; i = 1\ldots N, \; j = 1\ldots L \end{aligned}$$

(22)

Both the objective function and constraints in Eq. (22) are linear in $\mathbf{Y }$ and $\theta$. Hence, we can solve the Eq. (22) with a linear programming efficiently. Algorithm 2 summarizes the pseudo code of the cutting plane algorithm. The algorithm converged within a maximum number of iterations (100 iterations in our experiments). The update of $\mathbf{Y }$ and ${\hat{\mathbf{Y }}}$ [i.e., Eqs. (21) and (22)] is solved with convex and simple linear programming problems, Eq. (18) is addressed efficiently.

3.5 How the proposal works

Except for efficient algorithms, it is also important to study how the proposal works. In the following, we show that the performance of our proposal is closely related to the correlation of base learners.

Theorem 1

Let $\mathbf{Y }^{GT}$ be the ground-truth label matrix and ${\hat{\mathbf{Y }}}^{*}$ be the prediction of SafeML, i.e., the optimal solution to Eq. (5). The performance of our proposal $\mathrm{perf}({\hat{\mathbf{Y}}}^{*}$, $\mathbf{Y }^{GT})$ w.r.t. $\hbox {F}_1$ score and Top-k precision is lower bounded by $\max \limits _{i=1,\ldots ,b}\min \limits _{j=1,\ldots ,b} perf (\mathbf{P }_i, \mathbf{P }_j)$ as long as $\mathbf{Y }^{GT} \in \varOmega$.

Proof

Let $f({\hat{\mathbf{Y }}}) = \min \limits _{\mathbf{Y }\in \varOmega } \,\, perf ({\hat{\mathbf{Y }}}, \mathbf{Y })$. Since ${\hat{\mathbf{Y }}}^{*}$ is the optimal solution to Eq. (5), the following inequality holds:

$$\begin{aligned} f({\hat{\mathbf{Y }}}^{*}) \ge f(\mathbf{P }_i), \;\;i = 1, \ldots , b \end{aligned}$$

(23)

which implies that

$$\begin{aligned} f({\hat{\mathbf{Y }}}^{*}) \ge \max \limits _{1 \le i \le b} f(\mathbf{P }_i) \end{aligned}$$

(24)

According to the definition of function f, for any i ($1 \le i \le b$) we have

$$\begin{aligned} f(\mathbf{P }_i) = \min \limits _{\mathbf{Y }\in \varOmega } perf (\mathbf{P }_i, \mathbf{Y }) \;\; \text{ where } \;\; \varOmega = \Big \{\mathbf{Y }\Big | \mathbf{Y }= \sum _{i=1}^{b}v_i \mathbf{P }_i \Big \} \end{aligned}$$

(25)

Since the Top-k Precision, $F_{1}$ score are used as performance measures, Eq. (25) can be reduced to

$$\begin{aligned} f(\mathbf{P }_i) = \min \limits _{\mathbf{v }} \sum _{j = 1}^{b}v_j \; perf (\mathbf{P }_i, \mathbf{P }_j) \;\; \text{ s.t. } \;\; \sum _{i=j}^{b}v_j = 1, v_i \ge 0 \end{aligned}$$

(26)

which naturally becomes,

$$\begin{aligned} f(\mathbf{P }_i) = \min \limits _{1 \le j \le b} \,\, perf (\mathbf{P }_i, \mathbf{P }_j) \end{aligned}$$

(27)

According to Eq. (24), we then have,

$$\begin{aligned} f({\hat{\mathbf{Y }}}^{*}) \ge \max \limits _{1 \le i \le b} \min \limits _{1 \le j \le b}&\,\, perf (\mathbf{P }_i, \mathbf{P }_j) \end{aligned}$$

(28)

Further note that $f({\hat{\mathbf{Y }}}^{*}) = \min \limits _{\mathbf{Y }\in \varOmega } \,\, perf ({\hat{\mathbf{Y }}}^{*}, \mathbf{Y })$ and $\mathbf{Y }^{GT} \in \varOmega$, we have

$$\begin{aligned} perf (\mathbf{Y }^{*}, \mathbf{Y }^{GT}) \ge f({\hat{\mathbf{Y }}}^{*}) \end{aligned}$$

(29)

Integrating inequations (28), (29), we then derive

$$\begin{aligned} perf (\mathbf{Y }^*, \mathbf{Y }^{GT}) \ge \max \limits _{1 \le i \le b} \min \limits _{1 \le j \le b}&\,\, perf (\mathbf{P }_i, \mathbf{P }_j) \end{aligned}$$

(30)

$\square$

Theorem 1 implies that the performance of SafeML is related to the maximin correlation of base learners. In practice, as shown in Table 9, it is often much better than direct supervised multi-label learning with only labeled data, which thus justifies the safeness of our proposal.

4 Experiments

To evaluate the effectiveness of our proposal, we conduct experimental comparisons with state-of-the-art methods on a number of benchmark multi-label data sets. We report our experimental setting and results in this section.

Table 2 Benchmark multi-label data sets

4.1 Setup

Data sets We evaluate the proposed method on nine multi-label data sets: emotions, enron, image, scene, yeast, arts, bibtex, tmc2007 and delicious. A summary of the statistics of data sets is shown in Table 2. $\#$inst is the number of instance in the data set; $\#$feat is the number of features; $\#$label is the number of labels; $\#$card-label is the average number of labels per example. The sample size ranges from 593 to more than 28,000. The feature dimensionality ranges from 72 to more than 1800. The label size ranges from 5 to 983. These data sets cover a broad range of properties.

Compared methods We compare the performance of the proposed algorithm with the following methods.

• BR (Binary Relevance) (Tsoumakas et al. 2009): the baseline method. A binary SVM classifier is trained on only labeled instances for each label.

• S4VM (Safe Semi-Supervised S V M) (Li and Zhou 2015): A binary S4VM classifier is trained on both labeled and unlabeled instances for each label.

• ML-kNN (Zhang and Zhou 2007) is a kNN style multi-label classification algorithm which often outperforms other existing multi-label algorithms.

• ECC (Ensemble Classifier Chain): state-of-the-art supervised ensemble multi-label method proposed in (Read et al. 2011).

• CNMF (semi-supervised multi-label learning by Constrained Non-negative Matrix Factorization) (Liu et al. 2006) is a semi-supervised multi-label classification algorithm via constrained non-negative matrix factorization.

• LEML (Low rank Empirical risk minimization for Multi-Label Learning) (Yu et al. 2014): recent state-of-the-art multi-label method for weakly labeled data by formulating the problem as an empirical risk minimization.

• TRAM (T R Asductive Multilabel Classification) (Kong et al. 2013) is a transductive multi-label classification algorithm via label set propagation.

• WELL (W Eak Label multi-Label method) (Sun et al. 2010) deals with missing labels via label propagation and controls the sparsity of label assignments.

Evaluation metrics Three criteria are used to evaluate the methods: Top-k precision (performance on a few top predictions) and $F_{1}$ score (including Macro $F_{1}$ and Micro $F_{1}$). In all cases, the experimental results of test data are computed based on the complete label matrix.

Each experiment is repeated for 30 times, and the average Top-k precision, Macro $F_{1}$ and Micro $F_{1}$ score on the unlabeled data are reported. We used libsvm (Chang and Lin 2011) as implementation for BR. For ML-kNN method, the distance metric used to find nearest neighbors is set as the Euclidean distance and the parameter k is set to 10. For ECC method, the number of base classifiers chains is set to 10. For the CNMF method, all parameters are set to the recommended ones in the paper. Parameters in LEML method are set as default value implemented by the author. For our SafeML method, the number of base learners b is set to 5 for all the experiments in this paper. The kernel type of SVM classifiers trained by all methods are set as RBF kernel on all data sets except enron, bibtex and tmc2007 for the number of features are large enough and standard linear SVM classifiers are trained. In the SafeML method, we generate pseudo label matrices $\mathbf{P }$ by training b base learners on labeled data for each class. In order to construct diverse base learners, a subset of labeled data is sampled randomly for each base learner. Parameter $\gamma _{0}$ is set to the average number of relevant labels for each example in training set multiplied by the number of testing instances.

Table 3 Macro $F_{1}$ and Micro $F_{1}$ score for the compared methods and our SafeML method with 15% labeled examples

Table 4 Top-k precision for the compared methods and our proposed method with 15% labeled examples

4.2 Results on semi-supervised multi-label learning

For each data set, we split 15% examples randomly as labeled data and other as unlabeled data. For BR method, a binary SVM classifier is trained for each class using only labeled data. For S4VM method, we train a S4VM classifier for each class with labeled and unlabeled data together.

The results measured in Macro $F_{1}$, Micro $F_{1}$ and Top-k precision are presented in Tables 3, 4 and Fig. 3. We can have the following observations.

• In terms of win counts, SafeML and ECC and TRAM perform the best on Macro $F_{1}$ and Micro $F_{1}$. SafeML and TRAM perform the best on Top-k precision. The other methods do not perform very well.

• In terms of average performance, SafeML obtains highly competitive performance with state-of-the-art methods on all the three multi-label evaluation metrics. SafeML obtains the best performance on Macro $F_{1}$ and Micro $F_{1}$.

• Importantly, in terms of loss counts, only SafeML does not degenerate performance significantly on three multi-label evaluation metrics, while the other methods all cause performance degeneration significantly in some cases.

• In both Macro $F_{1}$ and Micro $F_{1}$, S4VM degenerates performance seriously in some cases, pointing out that pure safe semi-supervised learning does not lead to safe multi-label predictions.

• Overall SafeML obtains highly competitive performance with state-of-the-art methods, while unlike compared methods that degenerate learning performance significantly in many cases, SafeML does not significantly hurt performance.

We have conducted experiments on a larger data set delicious which contains more than 900 labels. Similar to the behavior on the other data sets, the results (as shown in Fig. 3) in terms of five performance criteria (i.e., top-1 precision, top-3 precision, top-5 precision, macro $\hbox {F}_1$ and micro $\hbox {F}_1$) show that our proposal achieves highly competitive performance with state-of-the-art multi-label learning algorithms; more importantly, unlike previous methods which degenerate the performance in many cases, compared with direct supervised multi-label learning algorithm using only labeled data, our proposal does not suffer from this issue and achieves safe performance.

Fig. 3

Performance for the compared methods and our proposal on delicious data with 15% labeled examples

Table 5 Micro $F_{1}$ score for the compared methods and our proposed method for weak label learning setting

Table 6 Macro $F_{1}$ score for the compared methods and our proposed method for weak label learning setting

4.3 Results on weak label learning

For each data set, we create training data sets with varying portions of labels, ranging from 20% (i.e., 80% of the whole training label matrix is missing) to 95% (i.e., 5% of the whole training label matrix is missing). In each case, the missing labels are randomly chosen among positive examples of each class.

Fig. 4

Top-5 precision on weak label learning

The results measured in Micro $F_{1}$ and Macro $F_{1}$ are presented in Tables 5 and 6. We can have the following observations.

• As the number of missing relevant labels decreases, all methods generally clearly improve the learning performance.

• Although WELL generally improves performance significantly (30 cases in Table 5 and 34 cases in Table 6), it significantly decreases the learning performance in 9 cases in Table 5 and 3 cases in Table 6, where most cases happen on few missing relevant labels. The reason may owe to the fact that the baseline BR method becomes more competitive and thus WELL turns to be risky.

• LEML also often improves the learning performance (19 cases in Table 5 and 35 cases in Table 6), however, it still significantly decreases the learning performance in 18 cases in Table 5 and 3 cases in Table 6. Under the same reason, LEML typically degenerates the performance on few missing relevant labels.

• SafeML significantly improves the learning performance in 40 cases in terms of both the Micro $F_{1}$ and Macro $F_{1}$ metrics. More importantly, it does not suffer from performance degeneration on all the 80 cases. Further more, SafeML obtains the best average performance among all the comparison methods.

Figure 4 shows the results of Top-k precision on three representative data sets. The results on other data sets perform similarly. SafeML performs highly competitive performance with compared methods, while unlike compared methods that degenerate learning performance significantly in many cases, SafeML does not significantly hurt performance compared with baseline BR method.

Table 7 Micro $F_{1}$ score for the compared methods and our proposed method for extended weak label learning setting

Table 8 Macro $F_{1}$ score for the compared methods and our proposed method for extended weak label learning setting

4.4 Results on extended weak label learning

For extended weak label learning, we create training data sets with varying portions of labels, ranging from 20% (i.e., 80% of the whole training label matrix is missing) to 95% (i.e., 5% of the whole training label matrix is missing). The missing labels are randomly chosen among positive and negative examples of each class.

The results measured in Micro $F_{1}$ and Macro $F_{1}$ are presented in Tables 7 and 8. We can have the following observations.

• WELL improves performance significantly (23 cases in Table 7 and 26 cases in Table 8), however it significantly decreases the learning performance in 8 cases in Table 7 and 6 cases in Table 8.

• LEML also often improves the learning performance (29 cases in Table 7 and 34 cases in Table 8), however, it still significantly decreases the learning performance in 7 cases in Table 7 and 5 cases in Table 8.

• SafeML significantly improves the learning performance in 39/38 cases in terms of Micro $F_{1}$ and Macro $F_{1}$, respectively. More importantly, it does not suffer from performance degeneration on all the 80 cases. Moreover, SafeML obtains the best average performance among all the comparison methods.

Figure 5 shows the results of Top-k precision on three representative data sets. Results on other data sets perform similarly. SafeML obtains highly competitive performance with compared methods, while unlike compared methods that degenerate learning performance significantly in many cases, SafeML does not significantly hurt performance compared with baseline BR method.

4.5 Study on the effectiveness of the lower bound performance in Theorem 1

We now empirically study that the lower bound $\max \limits _{i=1,\ldots ,b}\min \limits _{j=1,\ldots ,b} perf (\mathbf{P }_i, \mathbf{P }_j)$ in Theorem 1 is an effective term. Specifically, we compare the derived lower bound with the performance of direct supervised multi-label learning. Table 9 shows the comparison results for $\hbox {F}_1$ score on five representative data sets in semi-supervised multi-label learning scenario with $15\%$ labeled data. The results on other setups behave similar. As can be seen, no matter for macro $\hbox {F}_1$ or micro $\hbox {F}_1$ measure, the lower bound performance derived in Theorem 1 is clearly better than that of direct supervised BR SVM. This demonstrates the effectiveness of the lower bound in Theorem 1 and the safeness of our proposal.

Table 9 Performance comparison between the lower bound in Theorem 1 and direct supervised multi-label learning

Fig. 5

Top-5 precision on extended weak label learning

4.6 Convergence and time complexity analysis

To generate pseudo label matrices, we train b base learners, which takes $O(b d N_{labeled} L)$ time and $N_{labeled}$ is the number of labeled data that usually far less than the size of whole data set. At each iteration of our cutting-plane algorithm, we get ${\hat{\mathbf{Y }}}$ by solving Eq. (15) as a linear programming, which takes $O(N_{test} L)$ time. In order to find the most violated constraint for the current ${\hat{\mathbf{Y }}}$, we solve a simple linear programming which takes $O(b^3)$ time. In total, this takes O(tNL) time, where t is the number of iterations and no more than 100 in our experiments. The convergence rate of our algorithm on two representative data sets is shown in Fig. 6, from which we can see that it converges in an efficient manner. The convergence rate of our proposal on other data sets performs similarly.

Fig. 6

The convergence rate of our proposal on two representative data sets

5 Conclusion

Multi-label learning with weakly labeled data is commonly occurred in reality. This includes, e.g., (i) semi-supervised multi-label learning where completely labeled examples are partially known; (ii) weak label learning where relevant labels of examples are partially known; (iii) extended weak label learning where relevant and irrelevant labels of examples are partially known. In this paper, we study to learn safe multi-label predictions for weakly labeled data, which means multi-label learning method does not hurt performance when using weakly labeled data. To overcome this issue, in this work we explicitly optimize multi-label evaluation metrics ($\hbox {F}_1$ score and Top-k precision) via formulating ground-truth label assignments are from a convex combination of basic multi-label learners. Although the optimization suffers from infinite number of possible ground-truth label assignments, cutting-plane strategy is adopted to iteratively generate the most helpful label assignments and consequently efficiently solve the optimization. Extensive experimental results on three weakly labeled learning tasks, namely, (i) semi-supervised multi-label learning; (ii) weak label learning and (iii) extended weak label learning, show that our proposal clearly improves the safeness when using weakly labeled data in comparison to many state-of-the-art methods.