Abstract
The risk estimator called “Direct Eigenvalue Estimator” (DEE) is studied. DEE was developed for small sample regression. In contrast to many existing model selection criteria, derivation of DEE requires neither any asymptotic assumption nor any prior knowledge about the noise variance and the noise distribution. It was reported that DEE performed well in small sample cases but DEE performed a little worse than the state-of-the-art ADJ. This seems somewhat counter-intuitive because DEE was developed for specifically regression problem by exploiting available information exhaustively, while ADJ was developed for general setting. In this paper, we point out that the derivation of DEE includes an inappropriate part, notwithstanding the resultant form of DEE being valid in a sense. As its result, DEE cannot derive its potential. We introduce a class of ‘valid’ risk estimators based on the idea of DEE and show that better risk estimators (mDEE) can be found in the class. By numerical experiments, we verify that mDEE often performs better than or at least equally the original DEE and ADJ.
Similar content being viewed by others
1 Introduction
The most famous approach of model selection is to derive a risk estimator and to choose the model minimizing it. This type of model selection includes cross-validation and so-called “information criteria” including AIC (Akaike 1973), BIC (Schwartz 1979), GIC (Konishi and Kitagawa 1996) and so on. Basically, information criteria have been derived by using asymptotic expansion, which requires the sample number n to go to the infinity. Though the cross-validation was not derived by asymptotic assumption, its unbiasedness or performance is guaranteed basically by asymptotic theory. For regression, Chapelle et al. (2002) proposed an interesting model selection criteria called Direct Eigenvalue Estimator (DEE). DEE has the following remarkable characteristics: (i) DEE is an approximately unbiased risk estimator for finite n. (ii) no asymptotic assumption (\(n\rightarrow \infty \)) is necessary to derive it. (iii) no prior knowledge about the noise variance and the noise distribution is necessary. Due to these virtues, DEE is expected to perform nicely for small sample cases. DEE requires two assumptions in its derivation instead of using the asymptotic assumption. The first assumption is that a large number of unlabeled data are available in addition to the labeled data. This assumption is often made in recent machine learning literatures and is practical because the unlabeled data can usually be gathered automatically. The other assumption is the most important assumption, which imposes statistical independence between the inside-the-model part and the outside-the-model part of the dependent variable y. This assumption holds not exactly in general but hold approximately. By numerical experiments, Chapelle et al. (2002) showed that DEE performed better than many of the conventional information criteria and the cross-validation. However, they also reported that another criterion ADJ (Schuurmans 1997) often performed better than DEE. It should be noted here that the comparison between ADJ and DEE is fair since ADJ also assumes that a lot of unlabeled data are available. Even though ADJ is the state-of-the-art, that result seems somewhat strange because DEE was derived specifically for regression by exploiting the properties of regression exhaustively while the derivation of ADJ is somewhat heuristic and was developed for general setting. By careful investigation, we found an inappropriate part in the derivation process of DEE, although the resultant form of DEE is ‘valid’ in a sense. As a result, DEE cannot derive its potential. To clarify these facts, we formulate the derivation process of DEE again and introduce a class of ‘valid’ risk estimators based on the idea of DEE. Then, we show that DEE belongs to this class but is not close to the optimal estimator among this class. Indeed, we can find several more reasonable risk estimators (mDEE) in this class. The variations arise from how to balance a certain bias-variance trade-off. The performance of mDEE is investigated by numerical experiments. We compare the performance of mDEE with the original DEE, ADJ and other existing model selection methods.
This paper is an extended version of the conference paper (Kawakita et al. 2010). We pointed out the above inappropriate part in the derivation of DEE and proposed a naive modification in the paper. However, theoretical analysis and numerical experiments are significantly strengthened in this paper.
The paper is organized as follows. We set up a regression problem and introduce some notations in Sect. 2. In Sect. 3, we briefly review the result of Chapelle et al. (2002) and explain which part is inappropriate in the derivation of DEE. In Sect. 4, a class of valid risk estimators are defined. We explain why DEE is valid but not close to the optimal estimator in this class. In addition, some modifications of DEE are proposed. All of proofs of our theorems are given in Sect. 5. Section 6 provided numerical experiments to investigate the performance of our proposal. The conclusion is described in Sect. 7.
2 Setup and notations
We employ a usual regression setting as reviewed briefly below. Let
 and
and
 . Suppose that we have training data
\(D:=\{(x_1,y_1), (x_2,y_2),\ldots , (x_n,y_n)\}\) generated from the joint density
\(p(x,y)=p(x)p(y|x)\) i.i.d. (independently and identically distributed), where
. Suppose that we have training data
\(D:=\{(x_1,y_1), (x_2,y_2),\ldots , (x_n,y_n)\}\) generated from the joint density
\(p(x,y)=p(x)p(y|x)\) i.i.d. (independently and identically distributed), where
 for each i. Here, we further assume the following regression model:
for each i. Here, we further assume the following regression model:
where
\(f_*(x)\) is a certain regression function belonging to
 and
\(\xi _i\) is a noise random variable which is subject to
\(p_{\xi }(\xi )\) with mean zero and variance
\(\sigma ^2\) and is independent of x. This implies that
\(p(y|x)=p_{\xi }(y-f_*(x))\). The goal of regression problem is to estimate
\(f_*(x)\) based on the given data set. To estimate
\(f_*(x)\), let us consider a model of regression function defined by
and
\(\xi _i\) is a noise random variable which is subject to
\(p_{\xi }(\xi )\) with mean zero and variance
\(\sigma ^2\) and is independent of x. This implies that
\(p(y|x)=p_{\xi }(y-f_*(x))\). The goal of regression problem is to estimate
\(f_*(x)\) based on the given data set. To estimate
\(f_*(x)\), let us consider a model of regression function defined by
where
\({\bar{\alpha }}=({\bar{\alpha }}_1,{\bar{\alpha }}_2,\ldots )^T\). Here, T denotes the transposition of vectors or a matrices. Just for convenience, we can assume that \(\{\phi _k(x)\}\) is a basis of  . If not, we can always extend it as such without loss of generality. By this assumption, there exists \({\bar{\alpha }}^*:=({\bar{\alpha }}^*_1,{\bar{\alpha }}^*_2,\ldots )^T\) such that \(f_*(x)\equiv f(x;{\bar{\alpha }}^*)\) almost everywhere. Our task now reduces to find an estimator \({\hat{f}}(x)\) of \(f(x;{\bar{\alpha }}^*)\) as accurate as possible. Its accuracy is measured by the loss function (Mean Squared Error) defined as
. If not, we can always extend it as such without loss of generality. By this assumption, there exists \({\bar{\alpha }}^*:=({\bar{\alpha }}^*_1,{\bar{\alpha }}^*_2,\ldots )^T\) such that \(f_*(x)\equiv f(x;{\bar{\alpha }}^*)\) almost everywhere. Our task now reduces to find an estimator \({\hat{f}}(x)\) of \(f(x;{\bar{\alpha }}^*)\) as accurate as possible. Its accuracy is measured by the loss function (Mean Squared Error) defined as
Here, \(E_{x,y}[\cdot ]\) denotes the expectation with respect to random variables x, y. Similarly, each expectation E has subscripts expressing over which random variables the expectation is taken. Since \(f(x;{\bar{\alpha }})\) essentially can express an arbitrary element of  , \(f(x;{\bar{\alpha }})\) itself is too flexible and tends to cause overfitting in general. Therefore, we usually use a truncated version of \(f(x;{\bar{\alpha }})\) as a model
, \(f(x;{\bar{\alpha }})\) itself is too flexible and tends to cause overfitting in general. Therefore, we usually use a truncated version of \(f(x;{\bar{\alpha }})\) as a model

where d is a positive integer. The ideal estimate of parameter \(\alpha \) is obtained by minimizing the loss function \(L\) in (3) with respect to \(\alpha \). However, \(L\) is not available because the distribution p(x, y) is unknown. Therefore, we usually minimize an empirical loss function based on D, which is defined as
For notation simplicity, we define \(y=(y_1,y_2,\ldots , y_n)^T\) and \({\varPhi }\) as \((n\times d)\) matrix whose (i, k) component is \(\phi _k(x_i)\). Then, \(L_D(f_d(\cdot ;\alpha ))=(1/n)\Vert y-{\varPhi }\alpha \Vert ^2\), where \(\Vert \cdot \Vert \) is the Euclidean norm. The estimator \({\hat{\alpha }}(D)\) minimizing \(L_D\) is referred to as Least Squares Estimator (LSE), i.e.,
We sometimes drop (D) of \({\hat{\alpha }}(D)\) for notation simplicity. An important task is to choose the optimal d. When d is too large, \(f_d\) tends to overfit, while \(f_d\) cannot approximate \(f_*(x)\) with too small d. To choose d, we assume that additional unlabeled data \(D_U:=\{x'_1,x'_2,\ldots ,x'_{n'}\}\) are available, where each \(x'_j\) is subject to p(x) independently. The number of unlabeled data \(n'\) is assumed to be significantly larger than n. Note that \(D_U\) is used not for parameter estimation but only for model selection as well as Chapelle et al. (2002). The basic idea to choose d is as follows. The following risk (expected loss function)
is often employed to measure the performance of the model. Hence, one of natural strategies is deriving an estimate of \(R^*(d)\) (denoted by \({\widehat{R}}_D(d)\)) using \(D\cup D_U\), and then choosing the model as \({\hat{d}}:=\mathop {\mathrm {argmin}}_{d}{\widehat{R}}_D(d)\). Many researchers have proposed estimators of \(R^*(d)\) so far. In the next section, we introduce one of such estimators, which was proposed by Chapelle et al. (2002).
3 Review of direct eigenvalue estimator
Most of past information criteria have been derived based on asymptotic expansion. That is, they postulate that \(n\rightarrow \infty \). In contrast, Chapelle et al. (2002) derived a risk estimator called DEE (Direct Eigenvalue Estimator) without using asymptotic assumption. In this section, we briefly review DEE and explain that its derivation includes an inappropriate part. As is well known, \(L_D(f_d(\cdot ;{\hat{\alpha }}(D)))\) is not an unbiased estimator of \(R^*(d)\). That is,
is not equal to zero. Let \(T^*(n,d)\) be
Using \(T^*(n,d)\), let us consider the following risk estimator
It is immediate to see that this estimator is exactly unbiased, i.e., \(\text{ bias }({\widehat{R}}_D^*(d))=0\). That is, \(T^*(n,d)\) is a so-called bias-correcting term. Remarkably, this estimator corrects the bias multiplicatively, whereas the most of existing information criteria correct the bias additively like AIC. Chapelle et al. (2002) showed that \(T^*(n,d)\) can be calculated as the following theorem.
Theorem 1
(Chapelle et al. 2002) Let \(\phi _1(x)\equiv 1\). Define \({\widehat{C}}:=(1/n){\varPhi }^T{\varPhi }\). Suppose that the following assumptions hold.
-
A1
Assume that \(\{\phi _k(x)|k=1,2,\ldots , d\}\) is orthonormal with respect to the expectation inner product \(<a(x),b(x)>_p:=E_x[a(x)b(x)]\), i.e.,
$$\begin{aligned} \forall k,\,\forall k',\quad <\phi _k(X),\phi _{k'}(X)>_p=\delta _{kk'}, \end{aligned}$$(7)where \(\delta _{kk'}\) is Kronecker’s delta.
-
A2
Let
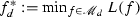 . Define \({\tilde{y}}_i:=y_i-f^*_d(x_i)\) and \({\tilde{y}}:=({\tilde{y}}_1,{\tilde{y}}_2,\ldots , {\tilde{y}}_n)^T\). Assume that $$\begin{aligned} \text {``}{\tilde{y}} \text { and } {\varPhi } \text { are statistically independent.''} \end{aligned}$$(8)
. Define \({\tilde{y}}_i:=y_i-f^*_d(x_i)\) and \({\tilde{y}}:=({\tilde{y}}_1,{\tilde{y}}_2,\ldots , {\tilde{y}}_n)^T\). Assume that $$\begin{aligned} \text {``}{\tilde{y}} \text { and } {\varPhi } \text { are statistically independent.''} \end{aligned}$$(8)
Then \(T^*(n,d)\) is exactly calculated as
See Chapelle et al. (2002) for the meaning of the assumption A2. A key fact is that Theorem 1 holds for finite n and the resultant form of \(T^*(n,d)\) does not depend on any unknown quantities except \(E_D[\mathrm{Tr}({\widehat{C}}^{-1})]\). In addition, it seems to be not difficult to find valid estimators of \(E_D[\mathrm{Tr}({\widehat{C}}^{-1})]\). Indeed, Chapelle et al. (2002) derived its estimator as
where \({\widetilde{C}}\) is defined by \({\widetilde{C}}=\frac{1}{n'}({\varPhi }')^T{\varPhi }'\) and \({\varPhi }'\) is an \((n'\times d)\) matrix whose (j, k) component is \(\phi _k(x'_j)\). The resultant risk estimator is called DEE and is given by
Note that the resultant bias correction factor is invariant under coordinate transformation. That is, the orthonormal assumption (7) can be removed by chance. However, this is somewhat queer. DEE was derived based on (9) but (9) is not invariant under coordinate transformation (it was derived by assuming the orthonormality of basis). Actually, (10) is not a consistent estimator of \(E_D[\mathrm{Tr}({\widehat{C}}^{-1})]\) in non-orthonormal case. This is because the derivation of estimator (10) includes an inappropriate part. We explain it in the remark at the end of this section. However, we must emphasize that the resultant form of DEE in (11) is valid as a risk estimator in a sense in spite of the above fact. Indeed, DEE dominated other model selection methods in numerical experiments, as reported by Chapelle et al. (2002). However, due to the inappropriate derivation, DEE cannot demonstrate its potential performance. We will explain it in details in the next section.
Remark
We explain here which part of the derivation of DEE is inappropriate. Chapelle et al. (2002) derived (10) as follows. First, they rewrote \(E_D[\mathrm{Tr}({\widehat{C}}^{-1})]\) as
where \(\lambda _k\) is the k-th eigenvalue of \({\widehat{C}}\). The subsequent part is described by quoting the corresponding part of their paper (page 16 of Chapelle et al. (2002)). Note that some notations and equation numbers are replaced in order to be consistent with this paper.
Quote 1
(Derivation of DEE) In the case when along with training data, unlabeled data are available (x without y), one can compute two covariance matrices: one from unlabeled data \({\widetilde{C}}\) and another from the training data \({\widehat{C}}\). There is a unique matrix P (Horn and Johnson 1985; Corollary 7.6.5) such that
where \({\varLambda }\) is a diagonal matrix with diagonal elements \({\lambda }_\mathbf{1},{\lambda }_\mathbf{2},\ldots , {\lambda }_\mathbf{d}\). To perform model selection, we used the correcting term in (9), where we replace \(E\sum _{k=1}^d1/\lambda _k\) with its empirical value,
However, Corollary 7.6.5 in Horn and Johnson (1985) does not guarantee the existence of a matrix P satisfying (12). We quote the statement of the corollary.
Quote 2
(Corollary 7.6.5 in Horn and Johnson (1985)) If \(A\in M_n\) is positive definite and \(B\in M_n\) is Hermitian, then there exists a nonsingular matrix \(C\in M_n\) such that \(C^*BC\) is diagonal and \(C^*AC=I\).
Here, \(M_n\) denotes the set of all square matrices of dimension n, whose elements are complex numbers. Furthermore, the symbol \(*\) denotes the Hermitian adjoint. As seen in the quote, the above corollary only guarantees that \(P^T{\widetilde{C}}P=I_d\) and \(P^T{\widehat{C}}P\) is diagonal. However, Quote 1 claims that \(P^T{\widehat{C}}P\) must be not only a diagonal matrix but also a diagonal matrix whose elements are equal to the eigenvalues of \({\widehat{C}}\) (See the bold part of Quote 1). This claim does not hold correct in general. Indeed, (13) is queer. Since (13) implies that \(\mathrm{Tr}({\widehat{C}}^{-1})=\mathrm{Tr}({\widehat{C}}^{-1}{\widetilde{C}})\) for any unlabeled data, unlabeled data play exactly no role.
4 Modification of direct eigenvalue estimator
In this section, we consider what estimators are valid based on the idea of Chapelle et al. and which estimator is ‘good’ among valid estimators. To do so, let us calculate the bias correction factor \(T^*(n,d)\) without the orthonormal assumption (7). As described before, the invariance of DEE under coordinate transformation was obtained based on the inappropriate way.
Theorem 2
Let \(\phi _1(x)\equiv 1\). Suppose that only the assumption A2 is satisfied in Theorem 1. Then \(T^*(n,d)\) is exactly calculated as
where \(C=[C_{kk'}]\) is a \((d\times d)\) matrix with \(C_{kk'}:=E_{x}[\phi _k(x)\phi _{k'}(x)]\).
See Sect. 5.1 for its proof. The form of (14) is invariant under coordinate transformation. It is natural because the definition of \(T^*(n,d)\) is invariant under coordinate transformation due to the property of LSE. There remain two unknown quantities C and \(V:=E_D[{\widehat{C}}^{-1}]\) in (14). Remarkably, both of them can be estimated using only the information about covariates x. Let us define \(D_0:=\{x_1,x_2,\ldots , x_n\}\) and \(D_x:=D_0\cup D_U\). Taking Theorem 2 into account, it is natural to consider the following class of risk estimators.
Definition 1
(a class of valid risk estimators) We say that a risk estimator \({\widehat{R}}_D(d)\) is valid (in the sense of DEE) if there exists a consistent estimatorFootnote 1 \({\widehat{H}}(D_x)\) of CV such that
We can easily understand that the resultant form of DEE is valid under some regularity conditions because \({\widetilde{C}}\) and \({\widehat{C}}^{-1}\) in (11) are statistically independent and are consistent estimators of C and V respectively. We imagine that Chapelle et al. knew the result of Theorem 2 because they implied this result in Remark 3 of Section 2.2 of Chapelle et al. (2002). Based on this fact, they seemingly recognized that the resultant form of DEE is valid. However, it is unclear that DEE is close to the optimal estimator in this class. In general, V is more difficult to estimate than C because V is based on the inverse matrix of \({\widehat{C}}\). More concretely, \({\widehat{C}}^{-1}\) tends to fluctuate more largely than \({\widehat{C}}\) especially when n is not large enough. Hence, spending more samples to estimate V seems to be a reasonable strategy. However, DEE spends the most of \(D_x\) (i.e., \(n'\) samples) to estimate C and spends only n samples to estimate V. Note that this strategy of DEE for estimation of CV has no necessity since the corresponding part was derived inappropriately. Therefore, let us discuss what estimators are good in among valid risk estimators. We start from the following theorem.
Theorem 3
Let \({\widehat{R}}_D\) be a valid risk estimator with \({\widehat{H}}(D_x)\). Define \({\widehat{R}}_D^*({\hat{\alpha }}):=T^*(n,d)L_D(f_d{\cdot ;{\hat{\alpha }}})\) with \(T^*(n,d)\) in (14). If \({\widehat{H}}(D_x)\) depends on only unlabeled data i.e., \({\widehat{H}}(D_x)={\widehat{H}}(D_U)\), then
Here, \(\mathrm{cov}(X,Y)\) denotes the usual covariance between X and Y and
The first term of the right side of (15) is independent of the choice of \({\widehat{H}}\). It expresses error of the ideally unbiased (but unknown) risk estimator \({\widehat{R}}_D^*(d)\). The second term is of order O(1 / n) while the third term is of order \(O(1/n^2)\). Therefore, it is natural to use an unbiased estimator of CV as \({\widehat{H}}\). If \({\widehat{H}}\) is unbiased,
where \(\text{ Var }({\widehat{H}})\) denotes a variance of \(\mathrm{Tr}({\widehat{H}})\). That is, as long as \({\widehat{H}}\) is unbiased, \({\widehat{H}}\) having the smallest \(\text{ Var }({\widehat{H}})\) gives the best performance. This fact motivates us to consider the following estimator. Let us divide the unlabeled data set \(D_U\) into two data sets \(D_U^1:=\{x'_1,x'_2,\ldots , x'_{n_1}\}\) and \(D_U^2:=\{x'_{n_1+1},x'_{n_1+2},\ldots , x'_{n_1+n_2}\}\) for estimating C and V respectively. Furthermore, we divide \(D_U^2\) into \(B_2:=\lfloor n_2/n\rfloor \) subsets such that the b-th subset is
As a result, each \(D_b\) is an i.i.d. copy of \(D_0\). Define \({\widehat{C}}_b\) as an empirical correlation matrix of \(\phi (x)=(\phi _1(x),\phi _2(x),\ldots ,\phi _d(x))^T\) based on \(D_b\). Then, it is natural to estimate V as
On the other hand, we can estimate C using \(D_U^1\) simply as
Then, we simply make \({\widehat{H}}_1:={\widehat{C}}_+{\widehat{V}}\). The resultant risk estimator is
We refer to this modified version of DEE as mDEE1. There are other possible variations depending on how to estimate C and V based on unlabeled data. We prepare the three candidates shown in Table 1. Both mDEE2 and mDEE3 construct \({\widehat{C}}_+,{\widehat{V}}\) and \({\widehat{H}}\) in the same way as mDEE1. We write \({\widehat{H}}\) used for mDEE1-3 as \({\widehat{H}}_1,{\widehat{H}}_2\) and \({\widehat{H}}_3\). While mDEE1 has no overlapped samples between \({\widehat{C}}_+\) and \({\widehat{V}}\), mDEE3 uses all unlabeled data to estimate both C and V. The other estimator mDEE2 is their intermediate. By checking some properties of these estimators, we have the following theorem.
Theorem 4
Assume that both \(n_1\) and \(n_2\) can be divided by n. Let \(B_1:=n_1{/}n\), \(B_2:=n_2{/}n\) and \(B:=n'{/}n\). Let \(\mu \) and \(\nu \) be column vectors obtained by vectorizing C and V respectively. Similarly, we vectorize \({\widehat{C}}_a\) and \({\widehat{C}}^{-1}_b\) as \({\hat{\mu }}_a\) and \({\hat{\nu }}_b\). We also define \({\hat{\mu }}\) and \({\hat{\nu }}\) as i.i.d. copies of \({\hat{\mu }}_a\) and \({\hat{\nu }}_b\). Then,
Furthermore, if we fix B (or equivalently n and \(n'\)), the variance of \(\mathrm{Tr}({\widehat{H}}_1)\) is minimized by the ceiling or flooring of
where
See Sect. 5.3 for its proof. The estimator mDEE1 seems to be the most reasonable estimator because its first order term O(1 / n) vanishes. Furthermore, \(\text{ MSE }({\widehat{H}}_1)=\mathrm{Var}(\mathrm{Tr}({\widehat{H}}_1))\) can be calculated explicitly as in Theorem 4. This is beneficial because the optimal balance of sample numbers used to estimate C and V, i.e., \(B_1^*\), can be estimated as follows. By the above theorem, it suffices to estimate the quantities \(a_1\) and \(a_2\) in order to estimate \(B_1^*\). Both quantities can be calculated if we know \(\mu \), \(\nu \), \(\mathrm{Var}({\hat{\mu }})\) and \(\mathrm{Var}({\hat{\nu }})\). We estimate them such as
Thus, we propose to choose the optimal \(B_1\) as the rounded value of (18) with \(a_1\) and \(a_2\) calculated by using the above empirical estimates.
In contrast to the case of mDEE1, the estimators mDEE2 and mDEE3 admit the bias. Therefore, we should discuss their performance through (15) instead (16). Then, we must care about MSE of \({\widehat{H}}\). Recall that MSE can be decomposed into bias and variance terms [(for example, see Hastie et al. (2001)], i.e.,
The estimators mDEE2 and mDEE3 are developed to decrease the variance of \({\widehat{H}}\) at cost of the bias increase. This is effective when the variance is much larger than bias. If the bias increases, the second term of (15) gets larger. When we can obtain unlabeled data as many as we like, \(\text{ bias }(\mathrm{Tr}({\widehat{H}}))\) can be decreased to zero as \(B\rightarrow \infty \) by Theorem 4. MSE also decreases to zero as \(B\rightarrow \infty \) because of the consistency of \({\widehat{H}}\). Nevertheless, if the number of unlabeled data is not enough, we have to take care which is better mDEE1 or mDEE2-3.
Many readers may think that the variance of \(\mathrm{Tr}({\widehat{H}}_2)\) should be calculated to estimate the optimal \(B_1\) for mDEE2. Surely, it is possible. However, the resultant form is excessively complicated and includes the third and the fourth cross moments. Hence, the resultant way to choose \(B_1\) is also computationally expensive and instable when d gets large. Thus, we do not employ the exact variance evaluation and survey the performance of mDEE2 by numerical simulations.
Finally, we review again DEE. DEE does not satisfy the assumption of Theorem 3 because \({\widehat{H}}\) of DEE utilizes \(D_0\). When \({\widehat{H}}\) is allowed to depend on \(D_0\), then we cannot obtain any clear result like Theorem 3. Hence, we cannot compare DEE and mDEE through Theorem 3. However, DEE looks similar to mDEE1 when \(B_1=B-1\) is selected. Since \(B_1\) of mDEE1 is optimized by the above way, mDEE1 does not necessarily behave similarly to DEE. Actually, it will be turned out by numerical experiments that the estimated \(B_1^*\) for mDEE1 tends to be very small compared to B. This fact indicates that the most unlabeled data should be used to estimate V. As a result, DEE does not exploit available data efficiently.
5 Proofs of Theorems
In this section, we provide proofs to all original theorems.
5.1 Proof of Theorem 2
Proof
We do not need to trace the whole derivation of DEE. The result for non-orthonormal cases is obtained by using (9) as follows. For convenience, let \(\phi (x):=(\phi _1(x),\phi _2(x),\ldots , \phi _d(x))^T\) for each d. Because the basis is not orthonormal, \(C=E_x[\phi (x)\phi (x)^T]\) is not an identity matrix. Using C, define
Then, \(\{\phi '_k(x)|k=1,2,\ldots , d\}\) comprises an orthonormal basis of \(\text{ Span }(\phi )\). Note that the LSE estimate of regression function does not change if we replace the original basis \(\{\phi _k(x)\}\) with this orthonormal basis \(\{\phi _k'(x)\}\). Therefore, using the basis \(\{\phi _k'(x)\}\), we obtain the same result as (14) except the replacement of \({\widehat{C}}\) with \({\widehat{C}}'=(1/n)({\varPhi }')^T{\varPhi }'\), where \(\phi '\) is a matrix whose (i, k) element is \(\phi _k'(x_i)\). Noting that \({\varPhi }'={\varPhi } C^{-1/2}\), we can rewrite \({\widehat{C}}'\) as
Substituting this into (14), we obtain a new version of (14) as
for non-orthonormal cases. \(\square \)
5.2 Proof of Theorem 3
Proof
The left side of (15) is calculated as
The last term is calculated as
The second last equality is obtained since \({\widehat{T}}(n,d)\) is statistically independent of D (\({\widehat{T}}(n,d)\) depends only on \(D_U\)). The second term of (19) is calculated as
The proof is completed by noting that
\(\square \)
5.3 Proof of Theorem 4
Proof
Let us partition the whole unlabeled data set \(D_U\) into subsets consisting of n samples. We write them as \(D_1,D_2,\ldots , D_B\). Then, we can write \(D^1_U=\cup _{a=1}^{B_1}D_a\) and \(D^2_U=\cup _{b=B_1+1}^{B}D_b\). As before, each empirical correlation matrix based on \(D_b\) is denoted by \({\widehat{C}}_b\). The bias of \({\widehat{H}}_1\) trivially vanishes because of the statistical independence between \({\widehat{C}}_+\) and \({\widehat{V}}\). As for mDEE2, it holds that
Taking expectation, we have
Hence, the bias of \(\mathrm{Tr}({\widehat{H}}_2)\) is
This does not depend on \(B_1\), so that \(\mathrm{Tr}({\widehat{H}}_3)\) has the same bias. Next, we calculate the variance of \(\mathrm{Tr}({\widehat{H}}_1)\). Let \({\mathcal {B}}_1 = \{ 1,2,\ldots ,B_1 \} \) and \({\mathcal {B}}_2 = \{ B_1+1, B_1 +2 ,\ldots , B \}\). Since \({\mathcal {B}}_1\) and \({\mathcal {B}}_2\) are disjoint, \( E \text{ Tr }({\hat{C}}_a {\hat{C}}^{-1}_b) = \mu ^T \nu \) for any \(a\in {\mathcal {B}}_1\) and \(b\in {\mathcal {B}}_2\). Hence, we have
We will make a case argument for the terms in the last summation. If \(c \ne a\) and \(b \ne d\), both factors are independent of each other. Hence, we have
If \(c=a\) and \(d \ne b\), we have
Similarly, if \(c \ne a\) and \(d=b \), we have
Finally, if \(c=a\) and \(b=d\),
Since the three terms in the last side are not correlated to each other, we have
Therefore, we have
Finally, we minimize the variance in terms of \(B_1\). Since B is fixed, \(B_2=B-B_1\). Using \(1/(B(B-B_1))=(1/B)(1/B+1/(B-B_1))\), \(\text{ Var }(\mathrm{Tr}({\widehat{H}}_1))\) is rewritten as
By regarding \(\mathrm{Var}(\mathrm{Tr}({\widehat{H}}_1))\) as a continuous function of \(B_1\) and differentiating it,
By setting this to zero, we obtain the second order equation of \(B_1\). Its solution is
It is easy to check that \((a_1+\sqrt{a_1a_2})/(a_1-a_2)\notin (0,1)\) while \((a_1-\sqrt{a_1a_2})/(a_1-a_2)\in (0,1)\). Since \(\mathrm{Var}(\mathrm{Tr}({\widehat{H}}_1))\) is convex in \(B_1\in (0,B)\), the minimum is attained by \((a_1-\sqrt{a_1a_2})/(a_1-a_2)\). Therefore, the optimal integer \(B_1\) is its ceiling or floor. \(\square \)
6 Numerical experiments
By numerical experiments, we compare the performance of mDEE with the original DEE and ADJ and other existing methods. We basically employ the same setting as Chapelle et al. (2002). Define Fourier basis functions \(\phi _k:\mathfrak {R}\rightarrow \mathfrak {R}\) as
The regression model \(f_d:\mathfrak {R}^M\rightarrow \mathfrak {R}\) is defined by
where \(x_m\) denotes the m-th component of x. Note that \(f_d(x;\alpha )\) cannot span  even with \(d\rightarrow \infty \) when \(M>1\). For each \(d=1,2,\ldots , {\bar{d}}\), we compute LSEFootnote 2
\({\hat{\alpha }}(D)\) for model
even with \(d\rightarrow \infty \) when \(M>1\). For each \(d=1,2,\ldots , {\bar{d}}\), we compute LSEFootnote 2
\({\hat{\alpha }}(D)\) for model  . Then, we calculate various risk estimators (model selection criteria) for each d and choose \({\hat{d}}\) minimizing it. The performance of each risk estimator is measured by so-called regret defined by the log ratio of risk to the best model:
. Then, we calculate various risk estimators (model selection criteria) for each d and choose \({\hat{d}}\) minimizing it. The performance of each risk estimator is measured by so-called regret defined by the log ratio of risk to the best model:
Here, \({\widehat{R}}_D(f_d(\cdot ;{\hat{\alpha }}(d)))\) expresses a test error, \({\widehat{R}}_D(f_d(x;{\hat{\alpha }}(d))):=\frac{1}{{\bar{n}}}\sum _{i=1}^{{\bar{n}}}(y''_i-f_d(x''_i;{\hat{\alpha }}(d)))^2\), where the test data \(\{(x_i'',y_i'')\,|\,i=1,2,\ldots , {\bar{n}}\}\) are generated from the same distribution as the training data. We compare mDEE1-3 with FPE (Akaike 1970), cAIC (Sugiura 1978) and cv (five-fold cross-validation) in addition to DEE and ADJ. In calculation of mDEE1, \(B_1\) (or \(n_1\)) was chosen according to the way described in Sect. 4. We also used the same \(B_1\) for mDEE2.
6.1 Synthetic data
First, we conduct the same experiments as that of Chapelle et al. (2002) as follows. We prepare the following two true regression functions,
where \(I(\cdot )\) is an indicator function returning 1 if its argument is true and zero otherwise. The sinc function can be approximated well by fewer terms in (20) compared to the step function. The training data are generated according to the regression model in (1) with the above regression functions. The noise \(\xi _i\) is subject to \(N(\xi _i;0,\sigma ^2)\) which denotes the normal distribution with mean 0 and variance \(\sigma ^2\). We prepare \(n=10,20,50\) training samples and \(n'=1500\) unlabeled data. Covariates \(x_i\) are generated from \(N(0,{\bar{\sigma }}^2)\) independently in contrast to Chapelle et al. (2002). Note that the above basis functions are not orthonormal with respect to p(x) in this case. The model candidate number \({\bar{d}}\) was chosen as \({\bar{d}}=8\) for \(n=10\), \({\bar{d}}=15\) for \(n=20\) and \({\bar{d}}=23\) for \(n=50\). The number of test data is set as \({\bar{n}}=1000\) in all simulations. We conducted a series of experiments by varying the regression function and the sample number n summarized in Table 2. In each experiment, \(\sigma ^2\) is varied among \(\{0.01,0.05,0.1,0.2,0.3,0.4\}\). The experiments were repeated 1000 times. The results are shown in Tables 3, 4, 5, 6, 7 and 8. These tables show the median and IQR (InterQuartile Range) of regret of each method.
As for these synthetic data, the performance of mDEE1-mDEE3 are almost same. Hence, we do not discriminate them here. When the true regression function is easy to estimate (i.e., \(f_1\)) and the noise variance \(\sigma ^2\) is small enough, DEE performs comparatively or a little bit dominated mDEE. Otherwise, all mDEE dominated DEE. Especially, mDEE is more stable than DEE because IQR of mDEE is usually smaller than that of DEE. Compared to ADJ, mDEE also performed better than ADJ except the case where \(\sigma ^2\) is small and the true regression function is \(f_1\). This observation holds to some extent in comparison with other methods. As a whole, mDEE is apt to be dominated by existing methods when the regression function is easy to estimate and the noise variance is almost equal to zero. In other cases, mDEE usually dominated other methods. Finally, we remark that the estimated \(B_1\) for mDEE1 took its value usually around \(1-20\). This fact indicates that \(V=E_D[{\widehat{C}}^{-1}]\) requires much more samples to estimate than C.
6.2 Real world data
We conducted the similar experiments on some real-world data sets from UCI (Bache and Lichman 2013), StatLib and DELVE benchmark databases as shown in Table 9. We used again (20) as the regression model. The number of model candidates \({\bar{d}}\) was determined by \(\lceil (n-1)/M \rceil \). We varied n as \(n=20,50\) in experiments. The total number of unlabeled data \(n'\) is described in Table 9. The test data number \({\bar{n}}\) was set to ‘total data number’\(-(n+n')\) in each experiment.
The results are shown in Figs. 1 and 2. First, we should mention that mDEE seemed to work poorly for the data sets “eeheat” and “eecool.” These data sets include discrete covariates taking only a few values. Thus, there are some sub data sets \(D_b\) in which the above covariates take the exactly same value. In such cases, \({\widehat{C}}_b^{-1}\) based on such \(D_b\) diverges to infinity. To see this, we show the histogram of \(\mathrm{Tr}({\widehat{C}}_+{\widehat{C}}_b^{-1})\) of mDEE3 for “eeheat” data with \(n=10\) in Fig. 3. From Fig. 3, we can see that some values of them take extremely large values. There are some ways to avoid this difficulty. The simplest way is to replace the empirical mean \(\frac{1}{B+1}\sum _{b=0}^B\mathrm{Tr}({\widehat{C}}_+{\widehat{C}}_b^{-1})\) in (17) with the median of \(\left\{ \mathrm{Tr}({\widehat{C}}_+{\widehat{C}}_0^{-1}),\mathrm{Tr}({\widehat{C}}_+{\widehat{C}}_1^{-1}),\ldots , \mathrm{Tr}({\widehat{C}}_+{\widehat{C}}_B^{-1})\right\} \). Applying this idea to mDEE3, we obtain a new criterion referred to as rmDEE (robust mDEE). Each panel of “eeheat” and “eecool” in Fig. 2 contains the result of rmDEE instead mDEE2. From Fig. 2, we can see that rmDEE worked significantly better than mDEE1 or mDEE3. On real-world data, mDEE1 slightly performed better than mDEE2 or mDEE3. However, their differences are little. In most cases, mDEE (or rmDEE) dominated DEE or at least performed equally. Remarkably, mDEE always dominated ADJ except ‘eeheat’ when \(n=20\). As a whole, mDEE (or rmDEE) often performed the best or the second best.
7 Conclusion
Even though the idea of DEE seems to be promising, it was reported that DEE performs worse than ADJ which was the state-of-the-art. By checking the derivation of DEE, we found that the resultant form of DEE is valid in a sense but its derivation includes an inappropriate part. By refining the derivation in the generalized setting, we defined a class of valid risk estimators based on the idea of DEE and showed that more reasonable risk estimators could be found in that class.
Both DEE and mDEE assume that a large set of unlabeled data is available. Even though these unlabeled data can also be used to estimate the parameter (i.e., semi-supervised learning), DEE and mDEE do not use them for parameter estimation. Hence, combining the idea of DEE with semi-supervised estimator is an interesting future work. However, it seems not to be an easy task because the derivation of DEE strongly depends on the explicit form of LSE.
Notes
That is, \({\widehat{H}}(D_x)\) converges to the true value CV in probability as n and \(n'\) go to the infinity.
To avoid the singularity of \({\varPhi }^T{\varPhi }\), we used Ridge estimator. However, its regularization coefficient is set to \(\lambda =10^{-9}\). Therefore, it almost works like LSE.
References
Akaike, H. (1970). Statistical predictor identification. Annals of Institute Statistical Mathematics, 22, 202–217.
Akaike, H. (1973). Information theory and an extension of the maximum likelihood principle. In Second international Symposium on Information Theory, pp. 267–281.
Bache, K, & Lichman, M. (2013). UCI machine learning repository. http://archive.ics.uci.edu/ml.
Chapelle, O., Vapnik, V., & Bengio, Y. (2002). Model selection for small sample regression. Machine Learning, 48, 9–23.
Hastie, T., Tibshirani, R., & Friedman, J. (2001). In The elements of statistical learning: Data mining, inference and prediction, Springer.
Horn, R., & Johnson, C. (1985). Matrix analysis. Cambridge: Cambridge University Press.
Kawakita, M., Oie, Y., & Takeuchi, J. (2010). A note on small sample regression. In Proceedings of 2010 international symposiumu on information theory and its applications, pp. 112–117.
Konishi, S., & Kitagawa, G. (1996). Generalized information criteria in model selection. Biometrika, 83(4), 875–890.
Schuurmans, D. (1997). A new metric-based approach to model selection. In Proceedings of the fourteenth national conference on artificial intelligence, pp. 552–558.
Schwartz, G. (1979). Estimating the dimension of a model. Annals of Statistics, 6, 461–464.
Sugiura, N. (1978). Further analysts of the data by akaike’ s information criterion and the finite corrections. Communications in Statistics—Theory and Methods, 7(1), 13–26.
Acknowledgements
This work was partially supported by JSPS KAKENHI Grant Numbers (19300051), (21700308), (25870503), (24500018). We thank the anonymous reviewers for useful comments. Some theoretical results were motivated by their comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor: Tong Zhang.
Rights and permissions
About this article
Cite this article
Kawakita, M., Takeuchi, J. A note on model selection for small sample regression. Mach Learn 106, 1839–1862 (2017). https://doi.org/10.1007/s10994-017-5645-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-017-5645-5





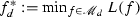 . Define
. Define 

