Gaussian conditional random fields extended for directed graphs

Abstract

For many real-world applications, structured regression is commonly used for predicting output variables that have some internal structure. Gaussian conditional random fields (GCRF) are a widely used type of structured regression model that incorporates the outputs of unstructured predictors and the correlation between objects in order to achieve higher accuracy. However, applications of this model are limited to objects that are symmetrically correlated, while interaction between objects is asymmetric in many cases. In this work we propose a new model, called Directed Gaussian conditional random fields (DirGCRF), which extends GCRF to allow modeling asymmetric relationships (e.g. friendship, influence, love, solidarity, etc.). The DirGCRF models the response variable as a function of both the outputs of unstructured predictors and the asymmetric structure. The effectiveness of the proposed model is characterized on six types of synthetic datasets and four real-world applications where DirGCRF was consistently more accurate than the standard GCRF model and baseline unstructured models.

1 Introduction

Structured regression models are designed to use relationships between objects for predicting output variables. In other words, structured regression models are using the given attributes and dependencies between the outputs to make predictions. This prior knowledge about relationships among the outputs is application-specific. For example relationships between hospitals can be based on similarity of their specialization (Polychronopoulou and Obradovic 2014), relationships between pairs of scientific papers can be presented as the similarity of sequences of citation (Slivka et al. 2014), relationships between documents can be quantified based on similarity of their contents (Radosavljevic et al. 2014), etc. The Gaussian conditional random fields (GCRF) model is a type of structured regression model that incorporates the outputs of unstructured predictors (based on the given attribute values) and the correlation between output variables in order to achieve higher prediction accuracy. This model was first applied in computer vision (Liu et al. 2007), but since then it has been used in different applications (Polychronopoulou and Obradovic 2014; Radosavljevic et al. 2010; Uversky et al. 2013), and extended for various purposes (Glass et al. 2015; Slivka et al. 2014; Stojkovic et al. 2016). A main assumption in the GCRF model is that if two objects are closely related, they should be more similar to each other and they should have similar values of the output variable. The similarity considered in GCRF is symmetric. However, in many real-world networks objects are asymmetrically linked (Beguerisse-Díaz et al 2014). Therefore, one limitation of the GCRF model is that the direction of link is neglected.

Networked data (such as social networks, traffic networks, information networks, etc.) are naturally modeled as graphs, where objects are represented as nodes, and relations are represented as edges between nodes. Many of these objects have directed links. For example, friendship strength is often not symmetric. In empirical studies (Michell and Amos 1997; Snijders et al. 2010) of friendship networks, participants are typically asked to identify their friends and to mark how close friends they are, which results in a directed graph in which friendships often run in only one direction between a pair of individuals. Another example is in social networks, such as Twitter or GitHub, where a user could follow all tweets posted by another user, or a developer could follow the work conducted by another developer. Also, in the email system, each individual communicates with one or more individuals by sending and receiving email messages, which results in a directed graph in which each edge has the number of sent emails as its weight.

The similarity matrix that quantifies the connections among the nodes of the graphs presented in these examples is an asymmetric matrix, and GCRF could not be directly applied on it since this model requires a symmetric matrix. One possible solution for this problem is to convert the similarity matrix from asymmetric to symmetric, which will probably cause loss of accuracy. To elaborate on this problem, we give an example of a relationship network at Fig. 1. Figure 1a presents the graph in which three nodes (marked A, B, and C) are linked with edges for which weights represent influence, in the sense that higher weight means higher influence. The edge from A to B means that A is influenced by B with weight 25. From this figure, we can conclude that node A is influenced by node C much more than by node B. On other hand node C is very much influenced by B, and not influenced at all by A. The influences from B to A, and from A to B, are the same. Converting this graph to an undirected one using the average approach results in the graph that is presented at Fig. 1b. If we look at this graph we will come to very different conclusions. Now the influence is bidirectional, which implies that connected nodes are mutually influenced with the same weight. Influence values on the relations B–A and C–A now have the same value, and nodes B and C are mutually influenced with a high weight. At Fig. 2 we presented how these structures can affect the predicted values, on the example of nodes B and C. First we will assume that values predicted by unstructured predictor (R) for nodes B and C are 100 and 10, respectively. At Fig. 2a these nodes are asymmetrically influenced, which means that predicted output ($\hat{\mathbf {y}}$) for the node C will get close to the output for the node B. On other hand, at Fig. 2b these nodes are symmetrically influenced, which means that predicted outputs for the nodes C and B will get close to each other. This example clearly illustrates how direction of the relation can affect the predicted value of the output.

Fig. 1

An illustrative example of a graph that represents influence between objects. a Directed graph and b Undirected graph

Fig. 2

An illustrative example of graph that represents influence between objects B and C, with corresponding values of the predicted output ($\hat{y}_{B}$ and $\hat{y}_{C}$). $R_B$ and $R_C$ are values predicted by unstructured predictor for nodes B and C. a Directed graph and b Undirected graph

In this work, we propose a new model, called Directed Gaussian Conditional Random Fields (DirGCRF), which extends the GCRF model by considering asymmetric similarity. The DirGCRF models the response variable as a function of both the outputs of unstructured predictors and the asymmetric structure. To evaluate the proposed model, we tested it on both synthetic and real-world datasets and compared its accuracy with standard GCRF, as well as with unstructured predictors Neural Networks and Linear Regression and simple Last and Average methods. All datasets and codes are publicly available.

We summarize contributions of this work as follows:

• 1. This is the first work that considers asymmetric links between objects in GCRF-based structured regression.

• 2. The proposed model considers both asymmetric structure and the outputs of unstructured predictor.

• 3. The effectiveness of the proposed directed model is characterized by experiments on six types of synthetic datasets and four real-world applications.

In the following, we first review related work in Sect. 2, followed by the details of the proposed method in Sect. 3. In Sect. 4 we provide the details about the datasets used and the experimental setup, as well as present experimental results. Finally, Sect. 5 consists of a summary of our findings, as well as future directions we intend to undertake with this project.

2 Related work

There exists a large corpus of research on regression and classification using graph based models (Table 1). Each approach takes different inputs and has various benefits and drawbacks. Some of these methods (Wytock and Kolter 2013) learn relationships between nodes from attributes. These are referred to as generative networks. On the other hand, discriminative network requires inputing the network structure (Radosavljevic et al. 2010; Altken 1935; Hallac et al. 2015). The origins of Gaussian conditional random fields (GCRF) model (Radosavljevic et al. 2010) lie in generalized least squares (GLS) (Altken 1935). In that model relationships between outputs are observed and affect the Mahalanobis distance in order to reduce training bias. GCRF leverages the same idea for multiple output regression.

Table 1 Survey of graph models literature

None of the above models can handle asymmetric link weights. However, this work is focused on advancing the GCRF model because it produces high accuracy and it is the most scalable learning approach of all listed above (Glass et al. 2015). GCRF has been used on a broad set of applications: climate (Radosavljevic et al. 2010, 2014; Djuric et al. 2015), energy forecasting (Wytock and Kolter 2013; Guo 2013), healthcare (Gligorijevic et al. 2015; Polychronopoulou and Obradovic 2014), speech recognition (Khorram et al. 2014), computer vision (Tappen et al. 2007; Wang et al. 2014), etc. There are other works that capture asymmetric dependencies, such as Asym-MRF model (Heesch and Petrou 2010). Since it is out of scope of this paper, for more details, please refer to Heesch and Petrou (2010) and Wang et al. (2005). Below we give a brief description of CRF and GCRF.

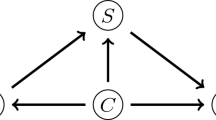
In a conditional random field (CRF) model, the observables $\mathbf {x}$ interact with each of the targets $y_i$ directly and independently of one another. For a general network structure, the outputs $\mathbf {y}$ also have independent pairwise interaction functions. Thus, the CRF probability function can be represented by an equation of the form:

$$\begin{aligned} P(\mathbf {y}|\mathbf {x})= \frac{1}{Z(\mathbf {x},\alpha ,\beta )} \exp \left( \sum _{i=1}^{N}A(\alpha , y_i ,\mathbf {x})+\sum _{j\sim i}I(\beta , y_i , y_j)\right) . \end{aligned}$$

There are two sets of feature functions, association potential (A) and interaction potential (I). The larger the value of A, the more $y_i$ is related to attributes $\mathbf {x}$. The larger the value of I, the more $y_i$ is related to $y_j$. Restricting these feature functions to be quadratic differences between a function of observables $R(\mathbf {x})$ and targets $\mathbf {y}$ produces a convex ensemble method:

$$\begin{aligned} A(\alpha , y_i , \mathbf {x}) = -\sum _{i=1}^{N} \sum _{k=1}^{K}\ \alpha _{k} (y_i - R_{i,k}(\mathbf {x}))^2, \end{aligned}$$

where $R_{i,k}$ represents output of unstructured predictor $R_k$ for node i, and K is the number of unstructured predictors, and N is the number of nodes. When incorporating quadratic pairwise interaction functions among outputs $\mathbf {y}$, a general graph structure ensemble method is obtained:

$$\begin{aligned} I(\beta , y_i , y_j) = - \sum _{l=1}^{L}\sum _{i \sim j} \beta _l S_{ij}^{l}(y_i - y_j)^{2}, \end{aligned}$$

where L represents the number of similarity functions, and $S_{ij}$ represents similarity between nodes i and j. This similarity is symmetric, which means that $S_{ij}=S_{ji}$.

The GCRF model is a CRF model with both quadratic feature and quadratic interaction functions that can be transposed directly onto a Gaussian multivariate probability distribution:

$$\begin{aligned} P(\mathbf {y}|\mathbf {x}) = \frac{1}{2\pi |\varSigma |^{1/2}}exp\left( -\frac{1}{2}(\mathbf {y}-\mu )^T Q (\mathbf {y}-\mu )\right) . \end{aligned}$$

When setting these two conditional probability models equal to one another, we get a precision matrix (Q) defined in terms of the confidence of input predictors and the pairwise interaction structure, measured by $\alpha$ and $\beta$ respectively. Let denote $L_j$ as the Laplacian matrix of pairwise interaction structure matrix $S_j$ for brevity:

$$\begin{aligned} Q=\sum _k\alpha _k I +\sum _j\beta _j L_j. \end{aligned}$$

Representing input predictions as a matrix R, the formula for the final prediction can be concisely written as:

$$\begin{aligned} \mu = Q^{-1}R \alpha . \end{aligned}$$

The only remaining constraint is that Q is positive semi-definite, which is a bound on convexity, but also a by-product of the multivariate Gaussian assumption. As long as the positive semi-definite constraint is satisfied, the model is convex.

In this work, the restrictions on symmetric link weights is relaxed, which alters the model in a way that is no longer capable of using a precision matrix. Additionally, convexity is no longer guaranteed. We will show convexity in special cases and demonstrate it empirically in Sect. 4.4.

3 Methodology

The proposed model DirGCRF is described in this section. Since asymmetric influence between objects violates some of the fundamental assumptions of the GCRF model (Radosavljevic et al. 2010), we re-derive the pseudo-Gaussian form and explain where the new formulation differs from the original. Below are the details of the derivation of a new matrix Q.

We start by showing that Gaussian normal form (GNF) can be equivalent to a conditional random field (CRF) model under certain conditions. The CRF is represented as:

$$\begin{aligned} P(\mathbf {y}|\mathbf {x})= \frac{1}{Z(\mathbf {x},\alpha ,\beta )} \exp \left( \sum _{i=1}^{N}A(\alpha , y_i ,\mathbf {x})+\sum _{j\sim i}I(\beta , y_i , y_j)\right) . \end{aligned}$$

The following is the exact formulation for the CRF as mentioned above. The summations are re-arranged so that the CRF can be shown to be equivalent with the GNF.

$$\begin{aligned} \sum _{i=1}^{N}A(\alpha , y_i ,\mathbf {x})+\sum _{j\sim i}I(\beta , y_i , y_j) = - \sum ^N_i \sum ^K_k \alpha _k (y_i - R_{i,k}(X) )^2 - \sum _{i \sim j} \sum ^L_l \beta _l S_{ij}^{l} (y_i - y_j)^2, \end{aligned}$$

(1)

where $\sim$ means that i is connected to j. Since the summation of all link weights is unchanged, by assuming that all nodes have a link weight of zero if not otherwise specified, we can rewrite Eq. 1 in a form which requires no outside information about the structure of S.

$$\begin{aligned} \hbox {Eq.}\,(1) = - \sum ^N \sum ^K \alpha _k (y_i - R_{i,k}(X) )^2 - \frac{1}{2} \sum ^N_i \sum ^N_j \sum ^L_l \beta _l S_{ij}^{l} (y_i - y_j)^2. \end{aligned}$$

Then the quadratic feature functions are expanded out. This allows us to group summations of independent linear and quadratic components.

$$\begin{aligned} \hbox {Eq.}\,(1)= & {} -\sum ^N\sum ^K \alpha _{k}y_{i}^{2} + \sum ^N\sum ^K 2\alpha _{k}y_{i}R_{i,k}(X) - \sum ^N\sum ^K \alpha _{k}(R_{i,k}(X))^{2}\\&+ \sum _{i}^{N}\sum _{j}^{N} \sum ^L_l \beta _l S_{ij}^{l} y_i y_j - \frac{1}{2} \sum _{i}^{N}\sum _{j}^{N} \sum ^L_l \beta _l (S_{ij}^{l} + S_{ij}^{l}) y_i^2 . \end{aligned}$$

The main difference between GCRF and DirGCRF is that the matrix S row sum, rowsum(S), is not equal to column sum, colsum(S). The equivalent conditions for the Conditional Random Field and Gaussian Normal Form Probability distributions are solved by segmenting the equation into quadratic, linear, and constant components. This is because the coefficients across the models differ but these variable degrees are the same across both models. This equivalence can then be solved as three different equivalences: quadratic coefficients, linear coefficients, and a constant component. In order to make this as clear as possible, the GNF is written using summations rather than matrix notation:

$$\begin{aligned} P(\mathbf {y}) = -\frac{1}{2} \mathbf {y}^T Q \mathbf {y} + \mathbf {y}^T b + c = \sum _{i}^{N}\sum _{j}^{N} Q_{ij} y_i y_j + \sum _{i}^{N} y_i b_i + c, \end{aligned}$$

where Q, b, and c are an arbitrary matrix, vector, and scalar for GNF. Equivalent conditions for the quadratic component are:

$$\begin{aligned} \begin{aligned} \sum _{i}^{N}\sum _{j}^{N} Q_{ij} y_i y_j =&\left( \sum ^K \alpha _{k}\right) \sum ^N y_{i}^{2} + \sum _{i}^{N} \sum ^L_l (rowsum(S_l) + colsum(S_l)) \cdot \beta _l y_i^2 \\&- \sum _{i}^{N}\sum _{j}^{N} \sum ^L_l \beta _l S_{ij}^{l} y_i y_j, \end{aligned} \end{aligned}$$

(2)

where summations over the coefficients $y_i^2$ are diagonal elements of Q and coefficients for $y_{i}y_{j}$ are off-diagonal elements of Q. Thus, the entries of Q can be segmented into a diagonal matrix, D (Eq. 3), plus a weighted adjacency matrix, A (Eq. 4):

$$\begin{aligned} Q= & {} D + A\nonumber \\ D_{ii}= & {} \left( \sum ^K \alpha _k\right) + \sum ^L \beta _l \frac{1}{2}(rowsum(S_l) + colsum(S_l) ) \end{aligned}$$

(3)

$$\begin{aligned} A_{ij}= & {} -\sum ^L \beta _l S_{ij}^l \end{aligned}$$

(4)

Let the Laplacian of an asymmetric similarity matrix be defined as:

$$\begin{aligned} L=-\frac{1}{2}(diag(rowsum(S)+colsum((S))-2S), \end{aligned}$$

then the new derived “precision” matrix (Q) can be concisely defined as:

$$\begin{aligned} Q = \left( \sum ^K \alpha _k\right) I + \sum ^L \beta _l L_l. \end{aligned}$$

When mapping the linear coefficients from CRF to GNF, one finds that the asymmetric network does not change the mappings as found in the original GCRF:

$$\begin{aligned} b_i = \sum ^K \alpha _K R_{i,k}(X), \end{aligned}$$

or, more concisely, $b=R\alpha$. Since the constant does not affect the marginalized likelihood, it can be omitted.

The Multinormal Likelihood Function ($P_{2}(\epsilon )$, Eq. 5) is equivalent to a Gaussian Normal Form ($P_1(\mathbf {y})$, Eq. 6) given certain conditions.

$$\begin{aligned} P_{2}(\epsilon )= & {} \frac{1}{Z}exp\left( -\frac{1}{2}\epsilon ^{T}\varSigma ^{-1}\epsilon \right) \end{aligned}$$

(5)

$$\begin{aligned} P_1(\mathbf {y})= & {} \frac{1}{Z} exp\left( -\mathbf {y}^{T}\varSigma ^{-1}\mathbf {y} + b^{T}\mathbf {y} + c\right) \end{aligned}$$

(6)

The equivalent conditions are:

$$\begin{aligned} c = -\mu ^{T}\varSigma ^{-1}\mu , \quad \mu =\varSigma b, \end{aligned}$$

where $\mu$ is the optimal prediction given the covariance matrix ($\varSigma$) and the linear component of the Gaussian Normal Form (b).

DirGCRF uses the above formulas and gradient ascent in order to find the optimal values for parameters $\alpha _i$ and $\beta _i$. The only remaining step is to find the first order derivatives of log-likelihood function and updates of $\alpha _i$ and $\beta _i$ in gradient ascent. Equation for the log-likelihood function (l) is:

$$\begin{aligned} l=-\frac{1}{2}\epsilon ^{T}Q\epsilon -Z. \end{aligned}$$

The partial derivatives of the precision matrix (Q) with respect to $\alpha _i$ and $\beta _i$ can be found as:

$$\begin{aligned} \frac{\partial Q}{\partial \alpha _{i}}=I \quad \frac{\partial Q}{\partial \beta _{i}}=L_{i}. \end{aligned}$$

Recall from the mapping of Gaussian Normal Form to Multinormal Likelihood Function, $\mu$ can be presented as:

$$\begin{aligned} \mu =Q^{-1}b. \end{aligned}$$

(7)

Since $\mu$ is in the log-likelihood function via $\epsilon = \mathbf {y} - \mu$, its partial derivatives with respect to $\alpha _i$ and $\beta _i$ are:

$$\begin{aligned} \frac{\partial \mu }{\partial \alpha _{i}}=-Q^{-1}IQ^{-1}b+Q^{-1}R_{i} \quad \frac{\partial \mu }{\partial \beta _{i}}=-Q^{-1}L_iQ^{-1}b. \end{aligned}$$

Fully elucidated form of the log-likelihood function is:

$$\begin{aligned} l=^+ -\frac{1}{2}(\mathbf {y}^{T}Q\mathbf {y}-\mathbf {y}^{T}Q\mu -\mu ^{T}Q\mathbf {y}+\mu ^{T}Q\mu )-log | Q^{-1} |^{2}. \end{aligned}$$

Minor steps in the remaining derivation of the partial derivatives with respect to the parameters $\alpha _i$ and $\beta _i$ are omitted. The final result is below, and is not hard to verify:

$$\begin{aligned} \frac{\partial l}{\partial \alpha _{i}}= & {} -\frac{1}{2}\left[ (\mathbf {y}-\mu )^{T}(\mathbf {y}-\mu )+(R_{i}-\mu )^{T}(I+Q^{-1}Q)(\mu -\mathbf {y}) \right] +\frac{1}{2}Tr(Q^{-1})\\ \frac{\partial l}{\partial \beta _{i}}= & {} -\frac{1}{2}\left[ \mathbf {y}^{T}L_{i}\mathbf {y}-(-Q^{-1}L_{i}\mu )^{T}Q\mathbf {y} -\mu ^{T}L_{i}\mathbf {y} + (-Q^{-1}L_{i}\mu )^{T}Q\mu \right] +\frac{1}{2}Tr(L_{i}Q^{-1}) \end{aligned}$$

4 Experiments

4.1 Datasets and experimental setup

4.1.1 Synthetic datasets

The purpose of experiments on synthetic data was to investigate the proposed model under controlled conditions on different types of graphs. Below are the descriptions of each type of graph and their node attributes and asymmetric similarities.

• Fully connected directed graph: Each pair of distinct nodes is connected by a pair of edges (one in each direction) with different weights.

• Directed graph with edge probability p: Directed graphs with different density. For each pair of distinct nodes, a random number between 0 and 1 is generated. If the number exceeds p, then the selected node pair will be connected with an edge.

• Directed graph without direct loop: Each pair of distinct nodes is connected by a single edge, which direction is chosen randomly. For example, if there is an edge from node A to node B, there could not be an edge from node B to node A.

• Directed acyclic graph: A graph with no cycles. For example, there is no path that starts from a node A and follows a consistently-directed sequence of edges that loops back to node A.

• Chain: All nodes are connected in a single sequence, from one node to another.

• Binary tree: A graph with a tree structure in which each node could have at most two children.

All these graph types are unlabeled and unweighted. Therefore, we randomly generated edge weights S and unstructured values R. The generated S and R were used to calculate the actual value of response variable $\mathbf {y}$ for each node, in accordance to the Eq. 7, with some added random noise. For calculation of $\mathbf {y}$ we needed to choose values for $\alpha$ and $\beta$ parameters. For GCRF based models, when there is only one $\alpha$ and only one $\beta$, only the ratio between values of $\alpha$ and $\beta$ parameters matters, not their actual values. A greater value of $\alpha$ means that the model is putting more emphasis on values that are provided by the unstructured predictor (R), while a greater value of $\beta$ means that the model is putting more emphasis on structure (S). We chose three different combinations in order to compare the performance of the model: (1) larger value of $\alpha$ parameter ($\alpha = 5, \beta =1$); (2) larger value of $\beta$ parameter ($\alpha = 1, \beta =5$); (3) same value of both parameters ($\alpha = 1, \beta =1$).

In all experiments on generated synthetic datasets one graph is used for training and five graphs for testing. For evaluating accuracy, experiments were conducted on graphs with 200 nodes. For testing run time, experiments were conducted on fully connected directed graphs with 500, 1K, 5K, 10K and 15K nodes.

4.1.2 Real-world datasets

We also evaluated our model on four real-world datasets: Delinquency (Snijders et al. 2010), Teenagers (Michell and Amos 1997), Glasgow (Bush et al. 1997) and Geostep (Scepanovic et al. 2015). The first three datasets contain data about habits of students (e.g. tobacco and alcohol consumption) and friendship networks at different observation time points. Geostep dataset contains data about treasure hunt games. Node attributes, edge weights, and response variables are extracted from data. All values were normalized to fit in range from 0 to 1. The experimental procedure and the obtained results are described in more detail in Sects. 4.3.1–4.3.4.

4.1.3 Baselines

The accuracy performance of DirGCRF was compared with the standard GCRF (Polychronopoulou and Obradovic 2014), and four nonlinear and linear unstructured baselines briefly described in this section: neural networks (NN) (Haykin 2009), linear regression (LR) or multivariate linear regression (MLR) (Weisberg 2005), average and last methods.

• GCRF: In order to apply the standard GCRF to the directed graphs, S matrix was converted from asymmetric to symmetric. In a symmetric matrix each pair of distinct nodes is connected by a single undirected edge, where the weight was calculated as an average of weights in the corresponding asymmetric matrix. The Neural Network unstructured predictor was used for both, DirGCRF and standard GCRF.

• NN: Neurons in feed-forward artificial neural networks are grouped in three layers: input, output and hidden layer. The number of neurons in the input layer was same as the number of features in the considered dataset. The number of neurons in the output layer was 1 for all datasets. The number of neurons in the hidden layer was selected based on the accuracy performance on the training data.

• LR or MLR: Linear regression or multivariate linear regression is used depending on the number of features in the considered dataset. Coefficients of predictors were trained on the features of all nodes on the training data, and then applied on the features on the test data to form the prediction.

• Last: In the real-world datasets, the graphs have evolved. Therefore, we consider one simple method, Last, which assigns values to the response variables using the same values as in the previous time point.

• Average: Another simple technique that calculates prediction of $\mathbf {y}$ value at each time stamp as the average of the $\mathbf {y}$ values in all previous time stamps.

To calculate the regression accuracy of all methods, we used $R^2$ coefficient of determination that measures how closely the output of the model matches the actual value of the data. A score of 1 indicates a perfect match, while a score of 0 indicates that the model simply predicts the output variable mean. $R^2$ of some poor predictors can even be worse than average and are characterized with negative coefficient of determination.

$$\begin{aligned} R^{2}= 1-\sum _{i} \frac{(y_i-\hat{y_i})^2}{(y_i-y_{average})^2}, \end{aligned}$$

where $\hat{y_i}$ is the predicted value, $y_i$ is the true value, and $y_{average}$ is the average of $\mathbf {y}$ values.

For DirGCRF and GCRF gradient ascent was used to find the optimal values for parameters $\alpha$ and $\beta$. Initial values of parameters were $\alpha =1$ and $\beta =1$, in each experiment. Learning rate was set to 0.01.

Table 2 Average (± standard deviation) $R^2$ of DirGCRF and GCRF on different types of asymmetric structures with parameters values $\alpha =5$ and $\beta =1$

All methods are implemented in Java, and experiments were run on Windows with 32GB memory (28GB for JVM) and 3.4GHz CPU. All codes are publicly available.¹

4.2 Performance on synthetic datasets

4.2.1 Effectiveness of DirGCRF

We first tested the accuracy of the DirGCRF model, and compared the performance against the standard GCRF model. Experiments were conducted on all synthetic datasets described in the Sect. 4.1.1. The outputs of unstructured predictor (R) and similarity matrix (S) are randomly generated. For each type of graph, one graph is used for training the model, and five graphs for testing. All graphs contain 200 nodes. $\alpha$ was set as 5 and $\beta$ was set as 1 in this experiment. Average $R^2$ and standard deviations of both models are presented in Table 2.

The results show that the DirGCRF produces higher accuracy than the standard GCRF on all synthetic directed graphs. On the fully connected directed graph, DirGCRF has 0.33 larger $R^2$ value than GCRF. With decreasing probability of edge existence, the graphs become sparser. Thus, the difference between DirGCRF and GCRF in accuracy becomes smaller. For graphs that do not have a direct loop or cycle, DirGCRF performs much better than GCRF, 0.53 and 0.73 larger $R^2$ value, respectively, which indicates the superiority of DirGCRF on directed graphs. Also, we noticed that in all experiments DirGCRF has very low standard deviation (from 0.007 to 0.00004) of $R^2$ performance.

The only exceptions are the results on the chains and binary trees where both algorithms have similar accuracy. This is expected since these structures are very sparse where every node has a maximum of two nodes that directly affect its output.

4.2.2 Accuracy with respect to different $\alpha$ and $\beta$ values

The purpose of this experiment is to find out how values of $\alpha$ and $\beta$ parameters in data generation process affect the accuracy of DirGCRF and GCRF models. In this experiment, we tested three different setups to generate synthetic graphs. In the first one, $\alpha$ has higher value, $\alpha = 5$ and $\beta =1$, which means that more emphasis is put on the unstructured predictor value and less on the structure. In the second one, both parameters have the same value: $\alpha = 1$ and $\beta =1$. In the third one, the $\beta$ parameter has higher value: $\alpha = 1$ and $\beta =5$, that is, more emphasis is put on the structure.

From Fig. 3, we can notice that the variations in $R^2$ value for DirGCRF across three different settings in all types of graphs are minor. However, there is a big difference in $R^2$ value for GCRF, especially on directed graphs and on directed graphs without loop or cycle. For example, in directed graphs a larger value of $\beta$ parameter caused a slight increase in accuracy of DirGCRF (from 0.92 to 0.96), but a large decrease in accuracy of GCRF (from 0.59 to −0.1) (Fig. 4). This indicates that the standard GCRF could not utilize asymmetric structure to provide good results, especially for datasets in which structure is more useful.

Fig. 3

Average $R^2$ of DirGCRF on different types of asymmetric structures with different $\alpha$ and $\beta$ values

Fig. 4

Average $R^2$ of GCRF on different types of asymmetric structures with different $\alpha$ and $\beta$ values

4.2.3 Run time

Time complexity of DirGCRF is same as time complexity of the standard GCRF (Radosavljevic et al. 2014). If the number of nodes in the training set is N and the learning process lasts T iterations, computation results in $O(\textit{TN}^3)$ time to train the model. The main cost of computation is matrix inversion.

The following speed tests of the DirGCRF model were conducted on synthetically generated fully connected directed graphs with varying numbers of nodes: 500, 1K, 5K, 10K and 15K nodes. The time consumption is presented after 50 iterations and the results are shown in Table 3. Model takes more time due to Java’s object-oriented nature, which requires more memory and more time to handle large matrix computations.

Table 3 Run time of DirGCRF for different number of nodes

4.3 Performance on real-world datasets

We have conducted experiments on four real-world datasets and compared the performance of DirGCRF against all baselines. We chose NN as the unstructured predictor for DirGCRF and GCRF, as it produces better results than LR\MLR. Details about each dataset are provided in Table 4 and they will be described in the following sections.

Table 4 Real-world dataset

4.3.1 Delinquency dataset

The Delinquency (Snijders et al. 2010) dataset² consists of four temporal observations of 26 students (aged between 11 and 13) in a Dutch school class between September 2003 and June 2004. For each observation, a friendship matrix is provided, as well as delinquency and alcohol scores. Both the delinquency and the alcohol scores are ranked from 1 to 5. The friendship networks were formed by allowing the students to name up to 12 best friends. The total number of edges in these matrices was between 88 and 133 (density from 13 to 20%). On average, 49% of students’ friendships were one-directional. The similarity ($S^t_{ij}$) from the student i to the student j at the specific time point t was calculated based on the friendship existence in all previous time points and the current one, that is,

$$\begin{aligned} S^t_{ij}=\frac{\sum _{k=1}^{t}S^k_{ij}}{t}. \end{aligned}$$

(8)

Fig. 5

Average $R^2$ for Delinquency dataset

The goal was to predict the delinquency level for each student. Training was performed on the observation points 2 and 3. Alcohol consumption and previous delinquency level were used as attribute values x. The models were tested on the observation point 4.

From the results presented at Fig. 5 we can see that the DirGCRF model outperforms all other competing models. The DirGCRF model has 8% larger accuracy than the standard GCRF model, and 4% larger accuracy than the Neural Network. Neural Network was the second best model. Multivariate Linear Regression was less accurate, but better than the Last and Average methods which produced negative $R^2$s. The GCRF model produces a lower $R^2$ than NN, which means that using converted symmetric friendship network was not helpful to improve the regression.

4.3.2 Teenagers dataset

The Teenagers (Michell and Amos 1997) dataset³ consists of three temporal observations of 50 teenagers (aged 13) in a school in the West of Scotland over a 3-year period (1995–1997). Just like in the Delinquency dataset the teenagers were asked to identify up to 12 best friends. The total number of edges in these observations was between 113 and 122 (density around 5%). On average 60% of teenagers’ friendships were one-directional. The same approach (Eq. 8) as in the Delinquency dataset was used to calculate similarity matrix. Besides friendship networks, the dataset contains information about teenager’s alcohol consumption (ranging from 1 to 5). The goal in this dataset was to predict alcohol consumption at the observation time point 3, based on two previous observations.

Figure 6 shows that the DirGCRF model has 17% larger accuracy than the standard GCRF model, and 4% larger accuracy than the Neural Network. Neural Network and Linear Regression have similar accuracy on this dataset, 0.35 and 0.34, respectively. The simple Last method has higher $R^2$ than both unstructured predictors and the same $R^2$ as DirGCRF, and the Average method also produced a high accuracy. This is due to the fact that in this application there are no additional features—only previous value of $\mathbf {y}$ was used to make predictions.

Fig. 6

Average $R^2$ for Teenagers dataset

4.3.3 Glasgow dataset

The Glasgow (Bush et al. 1997) dataset⁴ consists of three temporal observations of 160 students at a secondary school in Glasgow. Students were followed over a 2-year period starting in February 1995, when the students were aged 13, and ending in January 1997. We used data for 129 students who were present at all three measurement points. The friendship networks were formed by allowing the students to name up to six friends and to mark them from 0 to 2 as follows: 1—best friend, 2—just a friend, 0—no friend. The total number of edges in these matrices was around 362 (density 2%). On average 72% of students’ friendships were one-directional. In order to predict tobacco consumption, the following features were used as attribute values $\mathbf {x}$:

• Alcohol consumption (from 1 to 5).

• Cannabis consumption (from 1 to 4).

• Romantic relationship (indicates whether the student had a romantic relation at the specific time point).

• Amount of pocket money per month.

Graphs from the first two observation points were used for training, and the graph from third one was used for testing. From Fig. 7, we can see that DirGCRF model outperforms all other competing models, but almost all other baselines (except the simple Last and Average methods) have produced close $R^2$ values. There is a noticeable difference between models that are using asymmetric and symmetric structure, that is, DirGCRF has 5% higher accuracy than the standard GCRF.

Fig. 7

Average $R^2$ for Glasgow dataset

4.3.4 Geostep dataset

The Geostep (Scepanovic et al. 2015) dataset⁵ consists of data about 50 treasure hunt games. Each game can have maximum 10 clues and each clue belongs to one of 4 categories. The goal is to predict probability that the game can be used for touristic purposes. Features that were used as $\mathbf {x}$ values are: the number of clues in each category (business, social, travel, and irrelevant), game privacy scope, and game duration. We randomly chose 25 games for training and the rest of them were used for testing. A similarity matrix was created based on the games’ features. The similarity of game i to the game j ($S_{ij}$) is defined as the sum of the common number of clues in each category k in both games divided by total number of clues in the game i.

$$\begin{aligned} S_{ij}=\frac{\sum _{k=1}^{4} min(C^k_i,C^k_j)}{\sum _{k=1}^{4} C^k_i}, \end{aligned}$$

(9)

where $C^k_i$ is the number of clues in the category k for the game i.

From the results presented at Fig. 8, we can see that the use of this asymmetric structure significantly improved the result of Neural Network. On the other hand, the difference in accuracy between GCRF and NN is the highest on this dataset (accuracy of GCRF is 13% lower), which indicates that converting asymmetric similarity matrix to symmetric had negative impact on regression performance.

Fig. 8

Average $R^2$ for Geostep dataset

It can be noticed that, from Figs. 5, 6, 7 and 8, the accuracies of DirGCRF, GCRF and NN are consistent for all four real-world datasets. In each dataset DirGCRF has the highest accuracy, while GCRF has lower accuracy than Neural Network.

4.4 Convexity

The experimental results presented in the previous sections were obtained for a specific value of hyper-parameter $\theta$. The learning task was to choose the parameters $\alpha$ and $\beta$ to maximize the conditional log-likelihood. The additional experiments were conducted in order to empirically demonstrate model convexity for all used synthetic and real-life datasets. Results are presented at Figs. 9 and 10. In this experiment we incrementally increase $\theta$ from 0 to $\frac{\pi }{2}$. For each $\theta$ we calculate $\alpha$ and $\beta$ as $\alpha =sin(\theta )$ and $\beta =cos(\theta )$. Then we calculate log-likelihood with respect to these parameters and plot the values. These figures show that log-likelihood is a convex function of parameters $\alpha$ and $\beta$ and that its optimization leads to globally optimal solution. The only exception is the Binary Tree dataset in Fig. 9, where the kink on the left hand side of the curve does not show convexity for this network structure. However, the optimization procedure still finds the global maximum even when starting close to the local maximum. The fact that we can plot the entire likelihood function guarantees that we are finding the global maximum.

Fig. 9

Experimental demonstration of model convexity for synthetic datasets

Fig. 10

Experimental demonstration of model convexity for real-world datasets

5 Conclusions

In this paper, we introduced a problem of using structured regression for predicting output variables that are asymmetrically linked. A new model, called directed Gaussian conditional random fields (DirGCRF), is proposed. This model extends the GCRF model by considering asymmetric similarities among objects. To evaluate the proposed model, we tested it on both synthetic and real-world datasets. A significant accuracy improvement is achieved compared to standard GCRF: from 5 to 19% for real-world datasets and in average 30% for synthetic datasets. If the data has more emphasis on structure than on values that are provided by the unstructured predictor, then the DirGCRF model even doubles the accuracy of GCRF for some types of directed graphs. Also, the experimental results confirmed that the simple approach of converting an asymmetric similarity matrix to a symmetric one for GCRF has negative impact on regression performance. Since this model is implemented in Java, which takes time to handle large matrix computations, our plan for future work is to implement the model in a procedural or functional programming language in order to speed it up and make it more efficient for large datasets. We also plan to apply the DirGCRF model to other real-world applications and to demonstrate that our model can use multiple unstructured predictors (multiple $\alpha$ parameters) and multiple graphs (multiple $\beta$ parameters).