Abstract
The utility of a dense subgraph in gaining a better understanding of a graph has been formalised in numerous ways, each striking a different balance between approximating actual interestingness and computational efficiency. A difficulty in making this trade-off is that, while computational cost of an algorithm is relatively well-defined, a pattern’s interestingness is fundamentally subjective. This means that this latter aspect is often treated only informally or neglected, and instead some form of density is used as a proxy. We resolve this difficulty by formalising what makes a dense subgraph pattern interesting to a given user. Unsurprisingly, the resulting measure is dependent on the prior beliefs of the user about the graph. For concreteness, in this paper we consider two cases: one case where the user only has a belief about the overall density of the graph, and another case where the user has prior beliefs about the degrees of the vertices. Furthermore, we illustrate how the resulting interestingness measure is different from previous proposals. We also propose effective exact and approximate algorithms for mining the most interesting dense subgraph according to the proposed measure. Usefully, the proposed interestingness measure and approach lend themselves well to iterative dense subgraph discovery. Contrary to most existing approaches, our method naturally allows subsequently found patterns to be overlapping. The empirical evaluation highlights the properties of the new interestingness measure given different prior belief sets, and our approach’s ability to find interesting subgraphs that other methods are unable to find.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Mining dense subgraph patterns in a given graph is a problem of growing importance, owing to the increased availability and importance of social networks between people, computer networks such as the internet, relations between information sources such as the world wide web, similarity networks between consumer products, and so on. Graphs representing this type of data often contain information in the form of specific subsets of vertices that are more closely related than other randomly selected subsets of vertices would be.
For example: a dense subgraph pattern in a social network could represent a group of people with similar interests or involved in joint activities; a dense subgraph pattern on the world wide web could represent a set of documents about a common theme; and a dense subgraph pattern in a product co-purchasing network (in which products are connected by an edge if they are frequently bought together) could represent a coherent product group.
A multitude of methods have been proposed for the purpose of discovering dense subgraph patterns, most of which belong to one of three categories. The first category starts from the full graph, and attempts to partition it (typically in a recursive way) such that each block in the partition is in some sense densely connected while vertices coming from different blocks tend to be less frequently connected. The second category generalizes the notion of a clique, e.g. to sets of vertices between which only a small number of edges are absent. The third category attempts to fit a probabilistic model to the graph. This model is typically such that vertices belonging to the same ‘community’ (which forms a dense subgraph) are more likely to be connected.
Despite these differences, all approaches for dense subgraph mining are similar in implicitly or explicitly assuming a measure of interestingness for dense subgraph patterns, to be optimised by the dense subgraph mining algorithm. The interestingness measure used essentially affects two aspects of the dense subgraph mining process: the computational cost of finding the most interesting dense subgraphs, and the degree to which presenting this pattern helps the user to increase their understanding about the graph.
As such, the design of a dense subgraph mining method has been approached very much as an engineering problem, trading-off conflicting requirements. This approach has long seemed acceptable (and even inevitable) given that true interestingness of a dense subgraph pattern eludes objective formalisation anyway, as it is fundamentally subjective: interestingness can only be defined against the background of prior beliefs the user already holds about the graph. For example, it will be less of a surprise to a user to hear that a set of vertices believed to all have a high degree form a dense subgraph, than that an equally large set of supposedly low-degree vertices form a dense subgraph, and thus the latter is subjectively more interesting to that user.
Because of this, the most basic question: “How interesting is a given dense subgraph pattern to a given user?” has evaded rigorous scrutiny. Previous research does not shine much light on what this interestingness looks like, on whether any of the engineered interestingness measures approximate it well, and on whether it can be optimised efficiently. Yet, recent results on the formalisation of subjective interestingness and its applications to other exploratory data mining problems (De Bie 2011a, b) has made clear that this question is actually well-posed.
The main goal of this paper is to answer this important question. We do this by formalising subjective interestingness of dense subgraph patterns, defined in terms of a subset of vertices from the graph, against a background of two important classes of prior beliefs on the graph’s structure (Sect. 2). Figure 1 already provides a glimpse of this. That is, it depicts a toy example graph consisting of 16 vertices in which the most interesting subgraph patterns for two different prior beliefs are highlighted. If one only knows the average degree of the vertices in the network, then the orange, dashed subgraph is the most interesting pattern according to our framework. If, on the other hand, one knows the individual degrees of the vertices, the orange subgraph is no longer the most interesting one: since its vertices have high degrees, finding a dense subgraph consisting of these vertices is hardly surprising. The purple, dotted subgraph, however, is relatively dense given its individual degrees, and is therefore considered the most interesting subgraph.
After formalizing subjective interestingness, we make it clear how the resulting measures are different from previous proposals, holding the middle between measures based on absolute missing edge tolerance and measures based on relative missing edge tolerance (Sect. 4). Furthermore we propose two effective algorithms for finding the most interesting (set of) dense subgraph patterns (Sect. 3), one of which is a fast heuristic and the other exact and hence necessarily slower.Footnote 1 Our empirical results illustrate the effectiveness of the search strategies, how the results are (usefully) different from those of a state-of-the-art algorithm for mining dense subgraph patterns, how different prior beliefs matter in the determination of subjective interestingness, and how the proposed algorithms perform computationally (Sect. 5).
2 Subjective interestingness of dense subgraph patterns
2.1 Notation
A graph is denoted \(G=(V,E)\), where V is a set of n vertices (usually indexed using a symbol u or v) and \(E\subseteq V\times V\) is the set of edges. The adjacency matrix for the graph is denoted as \(\mathbf {A}\), with \(a_{u,v}\) equal to 1 if there is an edge connecting vertices u and v, and 0 otherwise.
For the sake of simplicity, we focus the exposition on undirected graphs without self-edges in this paper, for which it holds that \((u,v)\in E \Leftrightarrow (v,u)\in E\) and \((u,v)\in E\Rightarrow u\ne v\). However, most of our results immediately apply also to directed graphs or graphs that allow self-edges. We will briefly outline how in Sect. 2.3.1.
The setup in this paper is that the user knows (or has direct access to) the list of vertices V in the graph, and their interest is in improving their understanding of the edge set E. Thus, the data to be mined is the edge set E, and the data domain is \(V\times V\) (with the additional constraints for undirected graphs without self-loops).
2.2 Formalising dense subgraph patterns
The term ‘pattern’ has been overloaded numerous times in the wider data mining literature, so it is important to make it clear exactly what is meant by this term in the current paper. We adhere to the definition adopted in the general framework introduced by De Bie (2011a). There, a pattern is any piece of information about the data that limits its set of possible values to a subset of the data domain. In the present context, a pattern is any piece of information about the graph that limits the possible values of the edge set E to a subset of the data domain \(V\times V\). Note that this setup naturally accommodates iterative data mining: in each iteration the domain is further reduced by the newly presented pattern.
As the focus of the paper is on dense subgraph patterns, the kind of patterns we will use informs the user that the density of a specified vertex-induced subgraph is equal to or larger than a specified value. A pattern of this syntax can be uniquely specified by means of a pair \((W,k_W)\), where \(W\subseteq V\) is the set of vertices in the subgraph and \(k_W\) is a lower bound on the number of possible edges between these vertices that are actually present in the graph G. By \(n_W\) we will denote the number of possible edges between vertices from W, equal to \(\frac{1}{2}|W|(|W|-1)\) for undirected graphs without self-edges.
Continuing our example in Fig. 1, the orange, dashed pattern can be specified as \((\{1,2,3,4,5\},8)\), meaning that at least \(k_W=8\) edges exist between the vertices from \(W=\{1,2,3,4,5\}\). The number of possible edges, \(n_W\), equals 10, since \(|W| = 5\).
2.3 A subjective interestingness measure
Many authors have previously attempted to quantify the interestingness of dense subgraph patterns in objective ways (see Sect. 4). Each of these attempts is based on the intuition that a subgraph is more interesting if it covers more vertices, and if only few pairs of these vertices are not connected. However, they differ in how to quantify the number of missing edges (e.g. in a relative or in an absolute manner), and in how to trade-off these two aspects.
A general framework for formalising subjective interestingnessIn this paper we make no attempt at proposing an objective interestingness measure. Instead we use the framework proposed by De Bie (2011a, b), which lays out general principles for how to quantify the interestingness of data mining patterns in a subjective manner. This is done by formalising the interestingness of a pattern with respect to a so-called background distribution P for the data, which represents the belief state of the user about the data. More specifically, the background distribution assigns a probability to each possible value of the data according to how plausible the user deems it to be.
Given a background distribution, De Bie (2011a) argued that subjective interestingness of a pattern can be quantified as a ratio of two quantities:
-
The information content of the pattern, which is the negative log probability that the pattern is present in the data, computed using the background distribution.
-
The description length of the pattern, i.e. the length of the description needed to communicate the pattern to the user.
Roughly speaking, the reasoning behind this is the following. The uncertainty of the data miner about the data can be formalised by the code length for the data under a Shannon-optimal code with respect to that background distribution, which is the negative log probability of the data under the background distribution. Any pattern will affect the beliefs of the data miner, and hence the background distribution representing these beliefs. A pattern is more efficient for this particular user if it reduces this measure of uncertainty more strongly. Under reasonable assumptions, the effect of observing a pattern to the user’s belief state can be modelled by conditioning the background distribution P onto the pattern’s presence in the data. In that case, this reduction of the user’s uncertainty about the data can be quantified as the negative log probability of the event that the pattern is present under the background distribution. However, this uncertainty reduction should be considered relative to the effort needed to achieve it, i.e. relative to the complexity or description length of the pattern.
The centrality of the evolving background distribution in this framework ensures that it naturally captures the iterative nature of the exploratory data mining process. Indeed, upon observation of a pattern, the user’s beliefs will include the newfound knowledge of this pattern, resulting in a change in the background distribution. This update to the background distribution reflects the fact that the observation of a pattern may affect the subjective interestingness of other patterns (indeed, some patterns make others more or less plausible). Then the most interesting pattern with respect to the updated background distribution \(P'\) can be found, and the process can be iterated.
To use this framework, we need to understand how to formalise prior beliefs at the start of the mining process in an initial background distribution P, and how it evolves upon presentation with a pattern. It was argued the maximum entropy distribution subject to the prior beliefs as constraints is a good choice for the initial background distribution. For the evolution upon presentation with a pattern, it was argued that the background distribution should be conditioned on the presence of the pattern (De Bie 2011a).
Applying the framework to dense subgraph patterns While this abstract framework is generally applicable at least in principle, how it is deployed for specific prior beliefs, data, and pattern types, is often non-trivial. The first main contribution of this paper is to do this for the important case of dense subgraph patterns in a graph.
For dense subgraph patterns, the data consists of the edge set \(E\subseteq V\times V\), and the patterns are of the form specified in Sect. 2.2. Thus in the present section we will discuss the kinds of initial prior beliefs for such data that we will consider in this paper, and what the resulting background distribution is (Sect. 2.3.1); how the background distribution evolves upon presentation with a pattern (Sect. 2.3.2); how to compute the information content of the patterns we consider (Sect. 2.3.3); how to compute their description lengths (Sect. 2.3.4); and finally how the information content and description length are combined to yield the subjective interestingness measure proposed in this paper (Sect. 2.3.5).
2.3.1 The initial background distribution
Although the framework is general in principle with respect to which prior beliefs are incorporated, for concreteness we develop the details for two cases of prior beliefs.
-
(1)
Prior beliefs on individual vertex degrees In the more complex case, the user holds prior beliefs about the degree of each of the vertices in the graph. De Bie (2011b) showed that the maximum entropy distribution then becomes a product of independent Bernoulli distributions, one for each of the random variables \(a_{u,v}\), defined to be equal to 1 if \((u,v)\in E\) and 0 otherwise. More specifically, it is of the form:
$$\begin{aligned} P(E)= & {} \frac{1}{Z}\prod _{u<v} \exp ((\lambda _u+\lambda _v)\cdot a_{u,v}), \end{aligned}$$where Z is a normalisation constant (the ‘partition function’) equal to \(Z=\prod _{u<v}\left( 1+\exp ((\lambda _u+\lambda _v)\right) \), so that:
$$\begin{aligned} P(E)= & {} \prod _{u<v} \frac{\exp ((\lambda _u+\lambda _v)\cdot a_{u,v})}{1+\exp (\lambda _u+\lambda _v)}. \end{aligned}$$As a product of Bernoulli distributions, this distribution can conveniently be represented by a matrix \(\mathbf {P}\in [0,1]^{n\times n}\), where the rows and columns are indexed by the vertices, and where \(p_{u,v}= \frac{\exp (\lambda _u+\lambda _v)}{1+\exp (\lambda _u+\lambda _v)}\) denotes the probability that \(a_{u,v}=1\), i.e. that there is an edge between vertices u and v (note that for undirected graphs without self-loops \(\mathbf {P}\) is symmetric and has zeros on the diagonal).Footnote 2 The parameters \(\lambda _u\) and \(\lambda _v\) thus directly determine the probability \(p_{u,v}\) for the edge between vertices u and v: the larger \(\lambda _u\) and \(\lambda _v\), the larger this probability. Given the assumed degrees for the vertices as specified by the prior beliefs, inferring the value of these parameters \(\lambda _u\) is a convex optimisation problem, and the algorithm presented by De Bie (2011b) for doing that easily scales to millions of vertices.
-
(2)
Prior belief on the overall graph density In the more simple use case we consider here, the user only has a prior belief about the overall density of the graph (or equivalently, on the average vertex degree). It is easy to show that the maximum entropy distribution subject to this prior belief is also a product of Bernoulli distributions, but now with all entries \(p_{u,v}\) from \(\mathbf {P}\) equal to the assumed (relative) edge density. Thus, also in this use case the background distribution is a product distribution with a factor for each vertex pair, fully parameterised by a matrix \(\mathbf {P}\).
Other types of prior beliefs The above two types of prior beliefs will be used and discussed in detail throughout this paper. One can imagine plenty of alternatives though. Consider the situation where each vertex has certain properties (e.g. affiliations to companies, sports clubs, etc., of people in a social network). Then, the user could express an expectation regarding the fraction of vertex pairs that share any given property that are connected (e.g. users could express a belief that two people affiliated to the University of Bristol are connected in the social network with probability \(\hat{p}\)). Then, dense subgraphs would end up being more informative if they can be less easily explained by shared property values (e.g. communities of people with mostly different affiliations). Although this case is beyond the scope of the present paper, it would also lead to a background distribution that is a product of Bernoulli distributions, and hence to similarly tractable algorithms as the two prior belief types discussed above.
The number of prior belief types of possible interest is clearly unbounded, and the purpose of the paper is by no means to be comprehensive in this regard. Let us just note that although the computational cost of the algorithms will vary depending on the kinds of prior beliefs considered, the general approach outlined below is not specific for any kind of prior belief type.
2.3.2 Updating the background distribution throughout the mining process
Upon presentation of a pattern, the user’s belief state will evolve to become consistent with this newly acquired knowledge, which should be reflected in an update to the background distribution. More specifically, this updated background distribution \(P'\) should be such that the probability that the data does not contain the pattern is zero. To see what this means in the present context, let us introduce the function \(\phi _W\), which counts the number of edges within the vertex-induced subgraph induced by \(W\subseteq V\), i.e. \(\phi _W(E)=\sum _{u,v\in W, u<v} a_{u,v}\). Then, following the presentation of a pattern \((W,k_W)\) to the user, \(P'\) should be such that \(\phi _W(E)\ge k_W\) holds with probability one. Let us denote this set of consistent distributions as \(\mathcal {P}'\).
The question is though: which of those (typically many) distributions from \(\mathcal {P}'\) best represents the updated background distribution of the user? De Bie (2011a) presented arguments for choosing as updated background distribution the I-projection of the previous background distribution onto the set of distributions consistent with the presented pattern, i.e.:
Interestingly, the result of this optimisation problem is simply P conditioned onto the presence of the pattern (in De Bie 2011a this was shown in a more general setting). Unfortunately though, for the kind of data and pattern considered in the present paper, this conditioning leads to the introduction of a large number of dependencies, which would create significant computational difficulties. We thus need to look for an alternative, novel solution.
Fortunately, slightly relaxing the problem dramatically enhances tractability. Specifically, we relax the requirement that the pattern \((W,k_W)\) is present with probability one, to the requirement that this inequality holds in expectation only. Mathematically, this amounts to replacing the first constraint in Eq. (1) with:
Clearly, this is a relaxation: any Q satisfying the original constraint will satisfy the relaxed one. Furthermore, for W sufficiently large this relaxation seems to be tight. Although we have no formal proof for this, we have an argument based on the Asymptotic Equipartition Principle (Cover and Thomas 2012), which states that any sequence of random variables will in the limit become a so-called typical sequence. The principle suggests that if W is sufficiently large then any random subgraph over W drawn from the background distribution thus obtained, will be (close to) typical, meaning that it will have an actual number of edges close to the expected number.
The relaxed optimisation problem is thus:
This is a strictly convex optimisation problem, with a continuously differentiable objective and affine constraints in the problem variables Q(E).Footnote 3 This allows us to explicitly characterise the updated background distribution as follows:
Theorem 1
Let the background distribution P over \(V\times V\) be a product of independent Bernoulli distributions, defined by:
where \(a_{u,v}\) is an indicator variable equal to 1 iff \((u,v)\in E\). Then, the maximiser \(P'\) of optimisation problem (3) is again a product of Bernoulli distributions, defined by:
where
Here, \(\lambda _W\) is equal to 0 if \(\sum _E P(E)\phi _W(E)\ge k\), and \(\lambda _W\) is equal to the unique positive real number for which \(\sum _E P'(E)\phi _W(E)=k\) otherwise.
The proof is given in the “Appendix”.
Corollary 1
Using the same notation as in Theorem 1, and for \(u,v\in W\), it holds that \(\log \left( \frac{p'_{u,v}}{1-p'_{u,v}}\right) =\log \left( \frac{p_{u,v}}{1-p_{u,v}}\right) +\lambda _W\). I.e., the effect of updating the background distribution is that the log-odds of an edge between any pair of vertices \(u,v\in W\) is increased by \(\lambda _W\).
As the updated background distribution is again a product of independent Bernoulli distributions, the process of updating the background distribution can be iterated by repeatedly invoking the theorem. In each iteration, upon presentation of a pattern \((W,k_{W})\) a new variable \(\lambda _{W}\) would be introduced, which affects the probabilities of edges connecting vertices within W in such a way that their log-odds are increased by \(\lambda _W\). This is precisely how the background distribution is updated in the experiments below.
Remark 1
It would be inefficient to store the updated edge probabilities at each iteration of the mining process, as their number is quadratic in the number of vertices. Instead, it is much more efficient in practice to only store the \(\lambda _W\) variables, and to compute the probabilities from these as and when needed.
This can be done by exploiting Corollary 1, which implies that the log-odds of the probability of an edge between a pair of vertices \(u,v\in V\) is equal to the log-odds of this probability under the initial background distribution, plus the sum of the \(\lambda _W\) variables corresponding to all patterns \((W,k_{W})\) for which \(u,v\in W\).
The log-odds under the initial background distribution with prior beliefs on individual vertex degrees is equal to \(\lambda _u+\lambda _v\) for the vertex pair (u, v), and hence it can be computed in constant time by storing only |V| parameters. For the initial background based on a prior belief on overall density, the log-odds is a constant.
After showing the user a series of patterns \((W,k_{W})\), the odds for an edge between u and v will have become \(\lambda _u+\lambda _v+\sum _{W:u,v\in W}\lambda _{W}\) under the updated background distribution. This corresponds to an edge probability equal to \(\frac{\exp (\lambda _u+\lambda _v+\sum _{W:u,v\in W}\lambda _{W})}{1+\exp (\lambda _u+\lambda _v+\sum _{W:u,v\in W}\lambda _{W})}\).
Remark 2
Note that after updating, the constraints on the expected degrees of the vertices used in fitting the initial background distribution may no longer be satisfied. This should not be surprising and is in fact desirable, as the initial constraints merely reflect initial beliefs of the user. These beliefs can be incorrect or inaccurate, and will evolve after observing a pattern.
On the other hand, any constraint imposed by the observation of a pattern will remain satisfied throughout subsequent iterations in the mining process. This follows from the fact that \(\lambda _W\ge 0\), such that \(p'_{u,v}\ge p_{u,v}\): the individual edge presence probabilities can only increase after updating a background distribution at any stage in the mining process. Thus, the expected value of the functions \(\phi _W(E)\) can only increase, such that if \(\sum P'(E) \phi _W(E)\ge k\) following an iteration of the mining process, this inequality will continue to hold in later iterations.
2.3.3 The information content
The information content is the negative log probability of the pattern being present under the background distribution. Thus, to compute it we need to be able to compute the probability of a pattern under the background distribution. Here we will show how this can be done, exploiting the fact that from Sects. 2.3.1 and 2.3.2 we know that the initial as well as the updated background distributions considered in this paper are products of Bernoulli distributions. This means that the background distribution can always be represented by means of a matrix \(\mathbf {P}\) as detailed in Sect. 2.3.1.
Given a pattern \((W,k_W)\) and a background distribution defined by \(\mathbf {P}\), the probability of the presence of the pattern is the probability that the number of successes in \(n_W\) Bernoulli trials with possibly different success probabilities \(p_{u,v}\) is at least equal to \(k_W\). This can be computed reasonably (though not very) efficiently using the Binomial distribution as long as the background distribution is constant, i.e. \(p_{u,v}=p\) for all \((u,v)\in E\) (i.e. for all possible edges). It is harder if the background distribution is not constant though.
Fortunately, we can tightly upper bound this probability by means of the general Chernoff/Hoeffding bound (Chernoff 1952; Hoeffding 1963):
Theorem 2
Let \(X_1, X_2,\ldots , X_n\) be n independent random variables such that \(0\le X_k\le 1\) and \(\mathbf {E}\left[ X_k\right] =p_k\). Furthermore, let \(X=\frac{1}{n}\sum _{k=1:n}X_k\), \(p=\mathbf {E}\left[ X\right] =\frac{1}{n}\sum _{i=1:n} p_k\). Then, for \(\hat{p}>p\):
Here, \(\mathbf {KL}\left( \hat{p} \Vert p \right) \) is the Kullback-Leibler divergence between two Bernoulli distributions with success probabilities \(\hat{p}\) and p respectively, i.e. \(\mathbf {KL}\left( \hat{p} \Vert p \right) =\hat{p}\log \left( \frac{\hat{p}}{p}\right) +(1-\hat{p})\log \left( \frac{1-\hat{p}}{1-p}\right) \).
The general Chernoff/Hoeffding bound applies to our case where \(X_k\in \{0,1\}\) indicates the presence of an edge between some pair of vertices \((u,v)\in E\),Footnote 4 with probability of success equal to \(p_{u,v}\). Then, for any given vertex set \(W\subseteq V\), the value of p from the theorem is equal to: \(p_W=\frac{1}{n_W}\sum _{u,v\in W, u<v}p_{u,v}\), and \(\hat{p}\) from the theorem is equal to the ratio \(\frac{k_W}{n_W}\) of the number \(k_W\) of the \(n_W\) possible edges between pairs of vertices in W that are present. Thus, the theorem statement translates into:
so that
This bound is very tight, particularly for the relevant situation of large values of \(\hat{p}\).Footnote 5 Thus it seems warranted to take this bound as a proxy for the actual information content.
2.3.4 The description length
To present a pattern \((W,k_W)\) to a user its set of vertices W needs to be described. To do this, we assume that the cost of assimilating the fact that any vertex is part of W is \(\log {(1/q)}\) and \(\log (1/(1-q))\) for the fact that any vertex is not part of W. This means that the total description length is:
Thus, the description length is an affine function of the cardinality |W|, namely \(\text{ DescriptionLength }[(W,k_W)]=\alpha |W|+\beta \), with \(\alpha =\log \left( \frac{1-q}{q}\right) \), \(\beta =\log \left( \frac{1}{1-q}\right) \), and \(0 < q < 1\).Footnote 6
2.3.5 The subjective interestingness
In the general case, taking the ratio of the information content to the description length, the subjective interestingness is thus (up to a constant factor):
This is relatively easy to compute for a given pattern \((W,k_W)\). The most costly part is the computation of \(p_W\), which requires the computation of the average of \(n_W=O(|W|^2)\) numbers if \(p_{u,v}\) is not constant. However, in an algorithm exploring subgraphs by recursively expanding them by adding a vertex, computing \(p_W\) can be done efficiently based on its value for the subgraph of size \(|W|-1\) it is a direct expansion of, requiring only O(|W|) additions. Also the number of edges \(k_W\) can be computed recursively in a similar way.
2.3.6 A detailed example of subjective interestingness
The subjective interestingness that we just formalised, including the two cases of prior beliefs, was also used to obtain the example shown in Fig. 1. In particular, the orange, dashed subgraph is the pattern having the highest Interestingness when considering graph density as prior belief, and the purple, dotted subgraph is the pattern having the highest Interestingness when considering individual vertex degrees as prior belief. In both cases, \(q = 0.2\) was used; the effect of q is negligible for large networks, but a higher and more realistic value for q is required to obtain reasonable results on smaller graphs. Here, q can be loosely interpreted as the ‘expected probability’ for a random vertex to be part of a dense subgraph pattern.
When comparing the two most interesting patterns, it is immediately obvious that they are quite different. In fact, they are in different parts of the graph and their intersection is empty. When one only knows the average degree of all vertices, any high density subgraph is deemed interesting, as is common in most existing approaches to dense subgraph mining (although our formalisation of ‘density’ is different, see Sect. 4.3.1). With our approach, however, it is also possible to inject other prior knowledge and use this to make interestingness subjective. This is the key to the iterative mining scheme presented in Sect. 2.3.2, but also other types of prior beliefs can be considered. The case we consider in this paper is prior beliefs on the individual vertex degrees, which generally results in the discovery of smaller and sparser subgraphs that are nevertheless surprisingly dense considering the degrees of their individual vertices.
To study the effect of this prior belief in more detail, consider the matrix \(\mathbf {P}\) presented in Fig. 2. Each cell in the heatmap represents an edge probability, i.e. the probability \(p_{u,v}\) that vertices u and v are connected by an edge given the individual degrees of the vertices. Vertex 2, for example, has degree six and thus the highest degree of all vertices. Hence, its edge probabilities are higher than those of other vertices. The most likely edge is the one between vertices 1 and 2, with \(76.8\,\%\) probability. Given this probability, finding that vertices 1 and 2 are indeed connected is not very interesting, which is reflected by a low information content. Edges between vertices 5, 6, and 7 are not very probable though, and hence that subgraph pattern gets high information content and subjective interestingness. This results in a completely different pattern having the highest subjective interestingness compared to the case where only the graph density is known, which results in a matrix \(\mathbf {P}\) in which all edges are equally likely.
Edge probabilities given the individual vertex degrees as prior belief, for the graph given in Fig. 1. The vertex numbers correspond to the numbers given in the toy example graph. Probabilities on the diagonal are zero since no self-edges are considered; the use of undirected graphs results in symmetric matrices (Darker corresponds to high edge probability)
3 Algorithms
In this paper, our focus is on the interestingness measure and, more specifically, on formalising subjective interestingness. Because our interestingness measure is more complex than measures based on density only, the search for the most interesting dense subgraph pattern cannot be expected to be as efficient. The search is challenging indeed, but we nonetheless develop two practically scalable algorithms to do this. The second main contribution of this paper is the introduction of two algorithms for finding dense subgraph patterns in a graph. One uses a heuristic search strategy for maximum scalability, the other uses an exact search strategy for maximum accuracy.
3.1 Heuristic search
The first strategy we consider is local search by means of hill-climbing. The general approach here is to start from a small subgraph (the ‘seed’), and to recursively expand or shrink this subgraph in a greedy manner in order to improve its interestingness, until no further improvement is possible. The algorithm implementing this strategy is shown in Algorithm 1 (both for-loops iterate over the vertices in order of decreasing degree, to optimise practical efficiency and choose the vertex with highest degree in case of a tie).

The algorithm requires the recursive computation of the interestingness measure, and thus of \(k_{W'}\) and \(p_{W'}\) for \(W'=W\cup \{v\}\) or \(W'=W{\setminus }\{v\}\). Based on the values of \(k_W\) and \(p_W\) this can be done efficiently in O(|W|) time. Using these two quantities, computing \(\text{ Interestingness }(W',k_{W'})\) can then be done in constant time. For improved efficiency, we only consider expansions that keep the subgraph connected.
To limit the effect of the choice of the seed, we independently run the hill-climber for a number of seeds and finally pick the best result achieved. In an attempt to ensure promising seeds as a starting point, we consider the following seeding strategies:
- All :
-
Each of the separate vertices forms a seed, i.e. \(\{v \mid v \in V\}\).
- Uniform( k ) :
-
A selection of k of the vertices separately, selected uniformly at random from V but without duplicates.
- TopK( k ) :
-
The top-k vertices, separately, with respect to the interestingness of their corresponding neighbourhood-induced subgraphs (i.e. the vertex itself along with all its direct neighbours in the graph).
3.2 Exact search
On moderately sized graphs, exact search may be feasible. Besides being useful in its own right in such applications, comparing the results of the hill-climber with the results of an exact search algorithm on smaller data will give insight into the effectiveness of the hill-climber. Thus, we develop an exact best-first search strategy that is similar to the A* algorithm. This algorithm is investigated only for the constant background distribution, as that allows us to use discrete data structures that lead to a particularly efficient implementation.
Typically we are only interested in the most interesting pattern, possibly to be iterated after updating the background distribution if more than one pattern is desired. Hence, we could use an A*-type of algorithm if an optimistic estimate can be made, i.e. if an upper bound on the interestingness that any supergraph of a given subgraph pattern can achieve can be computed.
Given such an optimistic estimate, the A*-type algorithm maintains a priority queue of candidate subgraphs sorted in order of decreasing value of the optimistic estimate. Then, the first pattern from the priority queue is iteratively selected and for each vertex not yet part of it a new pattern is created by adding it to the pattern. The pattern is then removed and the expanded candidate patterns are inserted in the priority queue. This iterative process is repeated until the optimistic estimate of the first-ranked pattern is lower than the actual interestingness of the best pattern found so far.
While this can be done in general, for simplicity and speed, we develop it only for the case of a constant background distribution. This allows us to use discrete data structures and hence greater efficiency. In this case, \(p_W\) is independent of W and equal to the assumed edge density of the graph. Consequently, the interestingness for any expanded subgraph \(W'\supseteq W\) only depends on \(n_{W'}\) and \(k_{W'}\).
Given a certain size of \(W'\), the value for \(n_{W'}\) is fixed as \(n_{W'}=\frac{|W'|(|W'|-1)}{2}\) by definition. Thus we can compute an upper bound on the interestingness of \(W'\) by computing an upper bound on \(k_{W'}\), the number of edges in the vertex-induced subgraph induced by \(W'\). There are three different kinds of vertices in this subgraph:
-
1.
Edges connecting two vertices from W.
-
2.
Edges connecting a vertex from \(W'{\setminus }W\) with a vertex from W.
-
3.
Edges connecting two vertices from \(W'{\setminus }W\).
The number of vertices of the first kind is fixed and independent of \(W'{\setminus }W\). To compute a bound on the number of vertices of the second kind, we need for each vertex in \(V{\setminus }W\) the number of edges it has to vertices in W. This set of numbers can be computed very efficiently using fast set intersections on a sparse representation of E. Then the sum of the largest \(|W'{\setminus }W|\) such values is a bound on the number of vertices of the second kind.
To compute a bound on the number of vertices of the third kind, we need for each vertex in \(V{\setminus }W\) the degree within the subgraph induced by the vertices \(V{\setminus }W\). Again, this set of values can be computed very efficiently using fast set intersection operations. Then sum of the largest \(|W'{\setminus }W|\) such values, each thresholded at \(|W'{\setminus }W|\)-1 (since this is the maximum number of neighbours there can be within \(W'{\setminus }W\)), is a bound on the number of vertices of the third kind. Adding the (bounds on) the number of edges of each of these three kinds yields an upper bound on \(k_{W'}\), and thus on the interestingness of \(W'\) given its size. The overall upper bound can be found by computing the largest upper bound for all possible sizes of \(W'\). This can be efficiently done in a for-loop from |W| to |V|, iteratively computing an upper bound for each consecutive \(|W| < |W'| \le |V|\) and taking the maximum as global optimistic estimate. This loop can be broken as soon as there are no more edges of the second or third kind left that can be added.
Although this bound could be further tightened and developed also for the prior belief using individual degrees, this would come at the expense of additional computational cost. We therefore leave a thorough investigation of this topic for future work. As the empirical evaluation will demonstrate, the presented estimate is sufficiently tight to allow us to achieve our main goal: providing a reasonably fast baseline to compare the quality of the hill-climber’s results to, on a number of moderately sized graphs.
4 Discussion and related work
Our contributions are related to three different areas of research: the development of subjective interestingness measures in data mining; the development of instant and interactive methods for pattern mining; and the wider literature on dense subgraph mining. Here we discuss some insightful connections to each of these.
4.1 Subjective interestingness in data mining
The data mining literature, and the local pattern mining literature in particular, abounds with papers on the formalisation of interestingness for various kinds of patterns (see e.g. McGarry 2005; Geng and Hamilton 2006 for two surveys on the topic). Part of that work is focused on subjective interestingness measures, which are often conceived as measures that quantify the amount of ‘novelty’ or ‘surprise’ a pattern presents to the user. A recent survey on this topic (Kontonasios et al. 2012) distinguishes two main classes of approaches: the syntactic approaches, which often work by encoding the prior knowledge about the data in a set of rules, patterns, a taxonomy, or ontology; and the probabilistic approaches, which often represent the user’s knowledge about the data using a probability distribution of the data (specified explicitly or implicitly).
The generic approach from De Bie (2011a), on which the contributions in the present paper are built, belongs to the category of probabilistic approaches, and is most similar in spirit to the swap randomisation approach from Gionis et al. (2007), Hanhijarvi et al. (2009). The swap randomisation approach aims to capture the prior beliefs of the user in the form of a set of constraints, similar to De Bie (2011a). However, it does not attempt to represent the belief state of the user in the form of an explicitly represented background distribution. Instead, it is based on the ability to directly sample randomised versions of the data while maintaining the prior belief constraints satisfied, bypassing the need for the background distribution. These randomised data samples then allow one to compute an empirical p value for any given pattern, quantifying the amount of surprise it presents to the user, and hence its subjective interestingness.
There are a number of important advantages to the approach advocated in De Bie (2011a) though, related to the fact that having access to the explicit background distribution allows one to compute the interestingness analytically. This is crucially important, as the most interesting patterns will tend to have a very small p value, such that discerning between them using a swap randomisation approach would require an unrealistically large number of randomised data samples to be drawn. Second, it would be infeasible to mine the most interesting patterns directly using a swap randomisation approach, as it would require running the costly randomisation procedure at each step during the search process. With an analytically computable interestingness measure, however, this is feasible as demonstrated in the present paper.
Finally, we note that a comment often heard about subjective measures of interestingness is that they become objective measures as soon as the prior beliefs or background knowledge is fixed. This is of course the case: once the user is fixed, the subjectiveness is factored out and the interestingness is fully determined in principle. However, the particular aspect of an interestingness measure that makes it subjective is that this dependency on the user is made explicit by treating the user as a variable input to the interestingness function (see also Kontonasios et al. 2012), such that, at least in principle, it is possible to quantify interestingness for other users as well. It is to make this clear that in the present paper we considered two kinds of prior beliefs, rather than just one.
4.2 Instant and interactive pattern mining
A recent trend in the literature is the development of instant and interactive pattern mining techniques. van Leeuwen (2014) provides a recent overview, including open challenges for future research. Contributions in this area can be roughly classified into three categories.
The first category concerns pattern sampling algorithms, often also called output space sampling to emphasize the difference from data sampling; the latter simply reduces the size of the problem to reduce its complexity, whereas the former considers the complete problem but only returns a sample from the full solution set. Hasan and Zaki (2009) introduced a sampling framework based on the Metropolis–Hasting algorithm to sample from the output space of all frequent subgraphs, and showed that frequent patterns can be sampled, e.g., uniformly or proportional to support. Boley et al. (2011) presented a direct, hence more efficient sampling procedure for itemsets. Although these methods can be used to obtain small numbers of patterns, the patterns (1) can only be sampled according to some objective interestingness measure and (2) iterative mining, where each new result is interesting relative to all its predecessors, is currently not possible.
The second category concerns interactive mining algorithms that aim to infer some kind of subjective interestingness from user feedback. The first work in this direction, by Bhuiyan et al. (2012), proposed to use user feedback to adapt the sampling distribution of itemsets, and is therefore also closely related to the methods in the first category. More precisely, it performs Markov Chain Monte Carlo (MCMC) sampling of frequent patterns and the user is allowed to provide feedback by liking or disliking them. This feedback is used to update the sampling distribution, so that new patterns are mined from the updated distribution.
In similar spirit, Dzyuba and van Leeuwen (2013) proposed Interactive Diverse Subgroup Discovery (IDSD), an interactive algorithm that allows a user to provide feedback with respect to provisional results and steer the search away from regions that she finds uninteresting. Later, Boley et al. (2013) and Dzyuba et al. (2014) simultaneously (and independently) developed methods to learn pattern rankings using techniques from preference learning. Boley et al. also presented a working system for what they called ‘one-click-mining’, in which the preferences of the user for certain algorithms and patterns are learned. Nevertheless, only objective interestingness measures are used to mine patterns, which are then presented to the user. For each of these methods, prior beliefs and/or mined patterns can not be used to explicitly adapt interestingness, and iterative mining of a non-redundant set of interesting patterns is not possible.
The third and final category concerns working pattern mining systems / tools with a graphical user interface, that have been developed with a focus on instant and interactive use. A prime example is MIME (Goethals et al. 2011), for mining and browsing (frequent) itemsets according to a number of objective interestingness measures. These systems, however, first mine a (large) number of patterns and then give the user the opportunity to browse this collection; subjective interestingness and interative mining are not supported.
4.3 Dense subgraph mining
We now survey the most prominent and most directly related work on the topic of dense subgraph mining.
4.3.1 Structural measures
The number of possible ways in which interestingness or quality of a dense subgraph pattern can be formalised is enormous, owing to the number of ways in which density (or lack thereof) can be quantified. A non-exhaustive list includes the ratio of the number of edges to the number of possible edges in the subgraph (the relative edge density), which defines the notion of a quasi-clique (Abello et al. 2002; Uno 2010); the minimum number of vertices in the subgraph that each vertex in the subgraph is connected to, which defines the notion of a k-core (Seidman 1983); the maximum number of vertices in the subgraph that a vertex is not connected to, which defines the notion of a k-plex (Seidman and Foster 1978); and the average degree within the subgraph (Goldberg 1984) (misleadingly called the subgraph’s ‘density’). Most recently the edge surplus was proposed (Tsourakakis et al. 2013), which computes the number of edges in excess of the expected number of edges within the subgraph, assuming that each edge is present with the same probability. With \(\gamma >0\) a parameter, and the notation of the current paper:Footnote 7
The so-called Optimal Quasi-Clique (OQC) of a graph is then defined as the subgraph maximising the edge surplus.
Unfortunately, in most applications each of these measures exhibits a bias that makes it practically hard to use. For example, the relative edge density is easily maximised and made equal to 1 simply by considering very small subgraphs (e.g. containing 2 vertices connected by 1 edge). On the other hand, the average degree tends to be (trivially) large for large subgraphs, simply because there are so many vertices any vertex can possibly be connected to. Similarly, it is usually easy to find large k-cores, whereas it is trivially easy to find very small k-plexes. The edge surplus, in being an absolute difference between two quantities that grow with the size of the subgraph, tends to be larger for larger subgraphs simply by virtue of being larger.
Yet, an advantage of all these measures of interestingness is their transparency: it is easy to explain what they mean. However, although our proposed measure is relatively efficient to compute, at first sight its relation with these objective structural interestingness measures is less obvious.
Fortunately, we can make this relation more clear if we approximate the proposed measure using a linear upper bound in the region \(\hat{p} > p\) (note that \(\hat{p}\le p\) would never lead to an interesting pattern). The upper bound we will use, solely for the purpose of the discussion in this section and thus not for the experiments, is based on the following simple upper bound for the KL-divergence in the region \(\hat{p}>p\) (illustrated in Fig. 3):Footnote 8
where \(c(p)=\frac{\log {\left( 1/p\right) }}{1-p}\). Thus we can bound the information content as follows:
and we can bound the interestingness measure as follows:
The numerator in this approximating upper bound makes it clear that the proposed interestingness measure is similar to the edge surplus when \(\beta \) is large relative to \(\alpha \) (such that the denominator is approximately constant). A key difference though is that the expected number of edges in our measure is computed as \(p_Wn_W\), i.e. with respect to the background distribution (rather than being determined by a parameter \(\gamma \), the value of which is not related to prior beliefs or any other relevant information). Thus, this probability itself varies with the subgraph W considered. However, even ignoring this difference, the upper bound on the proposed interestingness measure differs from the edge surplus by a factor equal to an affine function of the number of vertices in the subgraph. This difference is desirable as further supported by the arguments below in Sect. 4.3.3.
The denominator normalises the edge surplus, and for \(\beta \) small relative to \(\alpha \) it makes this bound very similar to what could be called the average degree surplus, which for vanishing \(p_W\) would become equal to the average degree.
Thus, (the upper bound on) our proposed interestingness measure combines elements from a number of objective interestingness measures, in addition to providing a means of injecting prior beliefs. This connection to previously proposed measures, resolving the issues they individually suffer from, strongly corroborates the principles from De Bie (2011a) used to derive this interestingness measure.
4.3.2 Newman’s modularity measure
A problem shared by the structural measures listed above is that the subgraph patterns they reveal are often the result of common knowledge or statistically trivial information. Our proposed measure solves this issue by taking prior beliefs into account, and by assigning a high interestingness value only if the pattern is surprising against that background. To some extent, this idea also underlies the measure of modularity, which was proposed to evaluate the quality of a partition of a network into (non-overlapping) communities (Newman and Girvan 2004). Modularity is equal to the difference between the number of edges within the partitions and the expected number of edges based on the configuration model (random graph model with specific degree sequence).
However, our method is different to modularity as it quantifies interestingness of individual overlapping subgraphs and is not bound to a specific background distribution. Additionally, modularity is essentially an absolute measure (being equal to the difference between actual number of edges and expected number of edges), and as a result it has been found to prefer large subgraphs (sometimes even if these consist of two smaller subgraphs connected by just a single edge) (Fortunato and Barthelemy 2007). And finally, it is not designed to handle overlap between subgraph patterns as it is essentially evaluating the global partition of the data rather than the quality of a single subgroup individually.
4.3.3 Hypothesis-testing based measures
Our chosen pattern syntax is such that the probability of the pattern being present is directly equivalent to a p value. Here, the null hypothesis is represented by the background distribution P, and the test statistic is equal to the number \(k_W\) of edges connecting the vertices from the set W for the pattern considered. With this null hypothesis and test statistic, the p value would be equal to the probability to observe \(k_W\) or more edges connecting vertices from W in data sampled from P, which is precisely the probability of the pattern \((W,k_W)\). That means that the information content is logarithmically related to the weight of evidence (as quantified by the p value) the pattern provides against the background distribution. This is directly in line with approaches that advocate the use of (empirical) p values to rank patterns, such as the approaches based on swap randomisation (Gionis et al. 2007; Hanhijarvi et al. 2009). An important advantage of our approach is however that the p values are computed analytically, which means that they are more accurate, and more importantly, that we can use them dynamically during search, and this without expensive computations. (Note that it was already pointed out in De Bie (2011a) that p values are indeed a special case of the information content for particular types of patterns.)
Additionally, our approach trades off this p value (i.e. information content) with the description length of the pattern. This means that the most interesting pattern is not necessarily the most surprising one in the sense of the p value. There are good reasons for this in addition to the motivations in De Bie (2011a), related to the multiple hypothesis testing issue. Indeed, the more hypothesis tests are being considered, the higher the probability that one of them turns out to be significant by chance. Normalising with the description length is similar in spirit to a multiple testing correction, demanding a more significant p value for larger patterns to account for their higher complexity. As such the multiple testing effect is controlled, making it less likely that the most ‘interesting’ pattern is actually a fluke.Footnote 9
5 Experiments
In this section we will use the acronym SSG-c, for ‘Subjective SubGraph - constant’, to refer to our approach with a prior belief on the overall number of edges, and SSG-i, for ‘Subjective SubGraph - individual’, to refer to the background distribution incorporating prior beliefs on the degree of each individual vertex. In all experiments, q is set to \(q=0.01\). While not reported here, we observed that the results are very robust w.r.t. the choice of this parameter, especially for larger datasets.
The data sources and sizes of the datasets used for the empirical evaluation in this section are listed in Table 1.Footnote 10 Both variants of the algorithm, exact A* and heuristic hill-climber, have been implemented in C++Footnote 11.
5.1 Evaluation of the search methods
The main goals of this subsection are to evaluate (1) the hill-climber’s ability to find a pattern with (near-)maximal interestingness, and (2) scalability of the algorithms, with a focus on the exact A*-like algorithm.
Since the hill-climber depends on an initial seeding step, our first experiment investigates the effectiveness of the three seeding strategies. Table 2 shows the interestingness of the top-1 pattern and the time needed to compute it when using the hill-climber with any of the three seeding strategies, using \(k = 1\), 10, or 100 seeds for ‘Uniform’ and ‘TopK’ seeding. The numbers shown are averages over results obtained on all but the two largest datasets (IMDB-actors and DBLP), which are too large to run with ‘All’ seeding within a reasonable time.
From Table 2, we conclude that interestingness-based TopK seeding outperforms Uniform seeding. Furthermore, with 100 seeds it achieves the same result as by seeding with all vertices, while achieving a speed gain of about two orders of magnitude. Using only 10 seeds results in another order of magnitude speed gain, while the most interesting pattern found is almost always as good as the one found when using All seeding. In fact, for SSG-i it always finds a solution that is as good as when using all vertices as seeds.
Thus, to evaluate the effectiveness of the hill-climber, we use TopK seeding with \(k=10\) and 100 and compare it to the results obtained with the globally optimal A* algorithm. As an additional baseline, we also include results from naive exhaustive enumeration of all subgraphs (implemented by skipping the pruning step in the A* algorithm), for computational reasons restricted to subgraphs containing up to six vertices. As exhaustive search does not allow scaling further, we had to restrict this experiment to the six smallest graphs: Karate, Dolphins, Lesmis, Polbooks, Football, and Adjnoun. Table 3 shows average results, clearly demonstrating that the hill-climber succeeds in finding the near-best pattern (with 10 seeds) or the best pattern (with 100 seeds) at a dramatically reduced computational cost.
It is unclear from Table 3 how the exact algorithm scales: from the limited average runtime of only 8.2 s, it appears that it might be able to solve much larger problem instances. We investigate this by running the exact algorithm on random Erdős–Rényi graphs of varying size and density. The performance results are given in Table 4. From the results, it is evident that the number of candidate patterns increases as the network size increases. No matter the density of the network, at some point the number of candidates becomes so large that the memory limit of 2 Gb is exceeded. This is due to the fact that the priority queue containing future candidates becomes very long; memory rather than runtime is the bottleneck. We could postpone the breaking point by allowing more memory, but given the steep increase in the number of candidates this would allow only slightly larger networks to be used.
Although exact search with the A*-based algorithm is only feasible on moderately sized graphs, i.e. containing up to 100 s of vertices, the results in Table 3 show that pruning the search space is essential in making this possible. Compared to exhaustive enumeration of subgraphs containing up to six vertices, both the number of candidates and the computation time is reduced by two orders of magnitude. In other words, for moderately sized graphs the exact algorithm, including its pruning strategy, is an essential contribution as it enables the discovery of optimal patterns. We have to resort to heuristics to be able to discover patterns in larger networks though.
5.2 Evaluation of the interestingness measure
For the remaining experiments we will use the hill-climber with TopK seeding (\(k=10\)), as the previous subsection showed this search strategy to be very fast while closely approximating the optimal result. Moreover, it can also be used hassle-free on larger networks.
5.2.1 Effect of the prior beliefs
Here we investigate the effect of incorporating different kinds of prior beliefs by comparing SSG-c and SSG-i on all datasets considered (see Tables 5, 7). From Table 5 we observe that the average degree of the vertices in the most interesting subgraph according to SSG-c is almost always higher than when using SSG-i. This is to be expected, since for SSG-i high degrees may represent a partial explanation for high density and thus reduce the information content. But also intuitively this makes perfect sense: different prior beliefs about the data should lead to different results, and our subjective interestingness measure allows for this. Second, we observe that interestingness under SSG-c is typically higher than under SSG-i. This should be no surprise either, given the fact that the user knows less about the data and hence has more to learn about it. This explanation is corroborated by the fact that the difference in interestingness is larger if the difference in average degree is larger as well.
Focusing only on the columns for SSG-c and SSG-i in Table 7, we observe that different prior beliefs also lead to different structural properties of the identified subgraphs. SSG-c often finds larger subgraphs than SSG-i, but not always. On the smaller datasets SSG-i tends to find small cliques, but both their average degrees in Table 5 and inspection of these subgraphs shows that these do not contain any hub vertices with high degree; given the low degrees of their individual vertices, SSG-i considers these cliques to be informative and hence interesting.
5.2.2 Iterative pattern mining
As explained in Sect. 2.3.1, our approach is naturally suited for iterative application, as patterns presented in previous iterations can be incorporated into the background distribution for subsequent iterations. Table 6 shows some characteristics of the first 10 patterns found in this way, using SSG-i (i.e. initially incorporating prior beliefs on the individual vertex degrees). Besides total computation time, the table shows the proportion of the graph covered by the union of the 10 subgraphs (‘coverage’), and the average Jaccard index over all pairs of subgraphs. The average Jaccard shows that while overlap tends to be avoided, small overlaps do take place. This illustrates how incorporating the presented patterns into the background distribution helps to avoid redundancy in the resulting pattern set, while patterns can still overlap when this is informative. Coverage varies strongly depending on the dataset, suggesting that our measure adapts itself to the scale and the structure of the dataset. The smaller datasets could be completely ‘explained’ with tens of patterns, whereas more patterns would be required to cover the larger graphs.
The computation times presented in Tables 5 and 6 demonstrate that the hill-climber scales very well. For example, iterative mining of 10 patterns on the two graphs containing 100, 000+ vertices and up to millions of edges takes between 15 min and 1 h. This includes not only the search for the subgraphs, but also the initial computation and the iterative updating of the background distribution (which is generally very fast and therefore negligible in practice).
5.2.3 Comparison with alternative approaches
As is clear from Sect. 4, the approach that is most similar to ours, both in terms of interestingness measure and algorithmically, is the one searching for optimal quasi-cliques (OQC) by maximising the edge surplus (Tsourakakis et al. 2013). This approach is arguably also the current state-of-the-art in dense subgraph mining, and is thus the ideal comparison for our work. We therefore compare SSG-c and SSG-i with two algorithms presented in that paper: the Greedy (referred to as OQC-G) and the Local (OQC-L) search heuristic.
The results are summarised in Table 7. The leftmost columns contain SSG-i resp. SSG-c interestingness values as computed on the best patterns found by the SSG-i resp. SSG-c hill-climber and OQC-G. For OQC, we restrict our focus to the G variant because it is deterministic and hence always produces the same results. The purpose of this comparison is twofold: (1) to show that our interestingness formalisation is different from that of OQC, and (2) to show that our hill-climber finds better patterns according to our interestingness criteria. Both claims are clearly confirmed by the results, as we explain next.
OQC is conceptually closer to SSG-c than to SSG-i and on some datasets, such as Football, Email, and DBLP, it finds results that are equally good to those found by the SSG-c hill-climber. On average, however, our SSG-c hill-climber scores much better than OQC-G: 11.36 versus 7.53. With its more detailed prior belief, SSG-i aims at another range of patterns and succeeds in finding patterns that score much higher than OQC-G. On IMDB-ratings, for example, the pattern found by OQC-G gets a score of only 0.35, whereas our SSG-i hill-climber finds a subgraph with score 49.46. This demonstrates the power of our subjective interestingness measure, which can in principle be used in combination with a variety of prior beliefs, each of which results in different patterns.
Next, we compare the sizes of the best patterns found by the different algorithms. The size of the most interesting patterns according to SSG is sometimes smaller and sometimes larger when compared to OQC. SSG does tend to find subgraphs with higher edge densities though (with a few exceptions). The diameters for SSG are occasionally smaller but generally comparable. Most importantly, the triangle densities tend to be considerably higher for both SSG methods than for the OQC methods (again, with a few exceptions).
To sum up, in Tsourakakis et al. (2013) it was shown that OQC finds subgraphs that are denser than maximum density subgraphs (Goldberg 1984), but we here demonstrate that SSG often finds even denser subgraphs. And most importantly, SSG can use different prior belief sets, which leads to different results, as also indicated by the SSG interestingness results. Concretely, when SSG-i is used the resulting dense subgraphs generally do not contain any of the highest-degree vertices (hubs), because it is already known that they are located in dense regions of the graph (see also the average degrees in Table 5).
5.2.4 External evaluation
Here we investigate to which extent the patterns found in the IMDB-ratings resp. Artists datasets correspond to movie resp. music genres. Genre information was not used to generate the networks and this investigation can therefore be regarded as an external, independent evaluation. Of course, there is no guarantee that the most interesting patterns relate to movie or music genres as defined by humans. It is possible that movie tastes relate to movie properties other than genres as defined in the IMDB dataset, such as the actors playing, the director, or perhaps something less obvious. Similarly, there could be different reasons why music bands receive attention on Twitter than just the genre of their music. Thus, although the presence of an association between the patterns found and genres would be a validation of our approach, the absence of such an association could not be interpreted for the failure of the method.
Nevertheless, we do find that almost all of the top-10 patterns on both datasets are highly significantly related to one or several genres. For completeness we do not only present the external evaluation using the two variants of our method but also using OQC-G. As before, we restrict our focus to the OQC-G variant because it is deterministic.
Tables 8, 9 and 10 show which genres are significantly associated with each of the top-10 patterns of the IMDB-ratings dataset, for SSG-i, SSG-c, and OQC-G respectively. To determine significance, the p value is first computed using the hypergeometric test, after which it is multiplied with the number of genres (19) as a Bonferroni correction for multiple testing, and finally compared with a significance threshold of 1e\(-\)4. A very similar strategy is commonly used e.g. in bioinformatics, to determine which gene ontology terms are significantly related to a given set of genes.
Looking at the patterns in detail, SSG-i appears to find more niche genres whereas SSG-c and OQC-G tend to find sets of associated blockbusters seen (and liked) by many. For example, although SSG-c and OQC-G do not find the same top pattern, the three highest degree vertices in their respective top patterns are Pulp Fiction, The Matrix, and Fight Club. On the other hand the three highest degree vertices in the top pattern of SSG-i are the relatively unknown Orlando, Twelve O’Clock High, and Pieces of April. This is not surprising as SSG-c and OQC-G do not take into account the degree distribution.
The “–”s in Tables 8, 9 and 10 mean that there are no genres significantly associated with the respective patterns. However this does not mean that the movies in the pattern are not related but just that the pattern cannot be explained based on significant associations with genres. Upon closer inspection of these patterns, we noticed that pattern 7 in Table 9 contains films with a male main character, whereas pattern 2 in Table 8 contains old films mainly from the 60s, 70s and 80s. The full lists of movies in the top-10 patterns for SSG-i and SSG-c on this dataset can be found in the supplementary materialFootnote 12.
Tables 11, 12 and 13 show which genres are significantly associated with the top-10 patterns found in the Artists dataset, for SSG-i, SSG-c and OQC-G respectively. The p value is again computed using the hypergeometric test. As Bonferroni correction for multiple testing the result is multiplied with 181, which is the number of music genres which appear at least 3 times in this dataset. The significance threshold used now is 0.01 as the dataset is smaller.
By taking a closer look at the results on Artists we see that SSG-i tends to pick up patterns that correspond to rarer genres than SSG-c and OCQ-G, such as bhangra, world, afro pop and to a lesser extend trance. A pattern related to afro-pop is not contained at all in the top 10 patterns of SSG-c and OCQ-G. A pattern related to bhangra is also found by OQC-G though at a lower rank (10) than SSG-i (4). Also, a pattern related to trance is found by all methods though at rank 7 for SSG-c and OQC-G as compared to rank 2 for SSG-i. At first sight, the top pattern found by SSG-i may seem surprising, as rock is a very common genre. Turns out, however, that this subgraph is extremely dense (edge density 97 %), which is much denser than the second pattern (70 %). The complete list of artists for the top-10 patterns obtained with SSG-i and SSG-c can be found in the supplementary materialFootnote 13.
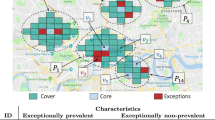
Finally, to illustrate the strengths of our approach, Fig. 4 visualises the top-10 patterns of SSG-i on the Artists datasetFootnote 14. The numbers of the patterns correspond to their ranks as shown in Table 11. Although patterns 7 and 8 have a lot of connections between them, our method was still able to distinguish afro-pop (8) as a distinct genre. Quite densely connected are also patterns 7 and 10, which also include an overlapping vertex (indicated in red). This makes sense as they are both significantly associated with hip hop.
5.3 Practical guidance
The experiments suggest the following three possible usage scenarios for our subjective subgraph mining framework.
The first scenario is the most obvious one, in which the user is actually able to express certain prior beliefs about the data. The particular cases considered in this paper are prior beliefs about the individual vertex degrees, or the overall edge density of the graph. This may be rather demanding in practice, but often still possible. For example the overall edge density is easy to specify and it is conceivable that the user genuinely has a prior belief about it. Note that this scenario allows for the prior beliefs to be incorrect, and if that is the case the most interesting patterns are likely to be patterns that provide evidence to rectify those incorrect prior beliefs.
In a second scenario, the user starts by a ‘shallow’ exploration of the data, prior to searching for the dense subgraph patterns. For example, they may compute the overall edge density (or estimate it by random sampling), or they may compute and scrutinise the individual vertex degrees. The result of this is that this information becomes part of their prior beliefs, after which the first scenario applies.
The third scenario is best explained by means of an example. In the Artists graph used in the experiments above, the user may not actually hold easily quantifiable beliefs about the degree of each Artist in the network. Yet, they may consider the degrees as irrelevant, i.e. they may want to see patterns that cannot easily be explained by individual degrees. The rationale could be that this information is easily verified by means of a simple lookup, such that for all practical purposes it can be consider prior information. In this scenario, it makes sense for the user to ask the system to find the most interesting patterns pretending that they are aware of the individual vertex degrees. In this case, the prior beliefs used should be based on the actual data (i.e. the actual vertex degrees), as in the second scenario.
6 Conclusions
Dense subgraph mining, as an exploratory data mining task, has long eluded the fact that the interestingness of a dense subgraph pattern is inevitably a subjective notion. While previous research has attempted to approach the problem by approximating interestingness in a number of ‘objective’ ways, in this paper we explicitly recognise its subjective nature and formalise interestingness by contrasting the dense subgraph patterns with a background distribution that formalises the user’s prior beliefs about the data. For concreteness, we focus on two important specific kinds of prior belief sets. Furthermore, we show how the resulting background distributions can be updated efficiently to account for the knowledge of patterns already found, thus allowing for an iterative data mining approach.
This subjective interestingness approach has considerable advantages, most notably the fact that it automatically adapts itself to the user. While we pay a price in terms of computation times as compared to important alternatives, we do present a performant exact, and a highly scalable and accurate heuristic algorithm for mining the most interesting patterns according to our measures.
For further work, we plan to explore increasing the number of prior belief types that can be dealt with along the lines of the discussion in Sect. 2.3.1. Another interesting line of further work is the generalisation of the dense subgraph pattern syntax to the multi-relational setting, which would result in a generalisation of the pattern syntax from Spyropoulou et al. (2014).
More practically, we anticipate that the proposed approach may lead to innovative applications in social media analysis, bioinformatics, recommendation systems, and many more. To highlight one possible application: in bioinformatics it has long been of interest to identify sets of co-expressed genes. This task is complicated by the fact that certain genes are expressed more often than others (e.g. housekeeping genes), such that any co-expression with these genes is less meaningful and potentially spurious. The strategy presented in the current paper could provide an innovative and natural way of dealing with that, when applied to a graph over the set of genes in which edges are an indication of co-expression. More generally, using our approach for such exploratory data mining problems where confounding factors (such as individual vertex degrees) are present, forms an exciting avenue for further work.
Notes
Note that we are interested in finding just the best pattern(s), rather than in enumerating them all as is common in the frequent pattern mining literature. The reason is precisely our focus on formalising subjective interestingness: if this is done adequately, by definition only the most interesting ones should be of interest to the user.
This model can be adapted to deal with graphs with self-edges, quite simply by changing \(u<v\) into \(u\le v\) below the product symbol. Additionally, it can be adapted to directed graphs. In that case, it is natural to assume prior beliefs on the in-degrees as well as the out-degrees of the vertices. This would result in a distribution of the form \(P(E)=\prod _{u,v}\frac{\exp ((\lambda _u+\mu _v)\cdot a_{u,v})}{1+\exp (\lambda _u+\mu _v)}\), where \(a_{u,v}=1\) indicates the presence of an arc from u to v in E, and the \(\lambda \) parameters affect the out-degree probabilities and the \(\mu \) parameters the in-degree probabilities. We refer to De Bie (2011b), for details.
Note that this optimisation problem will also always be feasible in our setting, as the value of k is found as \(\phi (E)\) on the actual data E, and hence a point distribution would always satisfy the constraint.
Note that the fact that \(0\le X_k\le 1\) in the general theorem suggests that it can be used also in a possible extension of our work for weighted graphs.
The bound only holds for \(\hat{p}>p\), but of course we are only interested in this situation (subgraphs that are denser than expected). The bound is tighter if the different values for \(p_{u,v}\) are more similar to each other, and thus in particular in the case where the user only holds a belief about the overall density, so that \(p_{u,v}=p\) for some constant p and \(p_W=p\).
Strictly speaking a small extra description of length \(\log (|W|)\) would be need to be added to account for encoding \(k_W\). However, for N or |W| sufficiently large this would become negligible, so we ignore it here for simplicity.
To be precise, Tsourakakis et al. (2013) actually define the edge density more generally, as a general parametric form of a subgraph interestingness measure, before proposing the specific form we reproduce here. Note however that our proposal is not a special case of that more general definition.
This bound could be tightened further without much loss of efficiency using a piece-wise linear upper bound.
Note that we do not explicitly limit the set of tests to those for patterns with a short description. Instead, we just use it to bias the choice of pattern towards simpler ones. This is similar in spirit to regularisation in machine learning, where any bias is good to effectively limit the hypothesis space in order to enhance generalisation.
Data sources are: Newman: http://www-personal.umich.edu/~mejn/netdata/; Arenas: http://deim.urv.cat/~aarenas/data/welcome.htm; Stanford: http://snap.stanford.edu/data/; HetRec: http://ir.ii.uam.es/hetrec2011/; OQC: kindly provided to us by the authors of Tsourakakis et al. (2013); IMDB-actors: co-actor graph directly extracted from http://www.imdb.com, available upon request; IMDB-ratings: combines movie data from http://grouplens.org/datasets/movielens/ with ratings from http://www.rottentomatoes.com/, two movies in the network are connected if at least two users gave both movies the maximal rating (5 out of 5), available upon request; Reverbnation Artists: constructed by using Twitter handles of music artists from http://www.reverbnation.com and making a network of artists where two artists are connected iff more than 10 people have tweeted about both of them.
Binaries and source code of SSG Miner are available for download at http://patternsthatmatter.org/software.php#ssgminer.
Available from http://patternsthatmatter.org/software.php#ssgminer.
Available from http://patternsthatmatter.org/software.php#ssgminer.
The respective results on the IMDB-ratings dataset could not be visualised due to the larger dataset and patterns.
References
Abello, J., Resende, M. G. C., & Sudarsky, S. (2002). Massive quasi-clique detection. In S. Rajsbaum (Ed.), LATIN 2002: Theoretical informatics. Lecture notes in computer science (Vol. 2286, pp. 598–612). Berlin, Heidelberg:Springer. doi:10.1007/3-540-45995-2_51.
Bhuiyan, M., Mukhopadhyay, S., & Hasan, M. A. (2012). Interactive pattern mining on hidden data: a sampling-based solution. In Proceedings of CIKM’12 (pp. 95–104).
Boley, M., Lucchese, C., Paurat, D., & Gärtner, T. (2011). Direct local pattern sampling by efficient two-step random procedures. In Proceedings of the 17th ACM SIGKDD international conference on knowledge discovery and data mining, August 21–24, 2011, pp. 582–590, San Diego, CA.
Boley, M., Mampaey, M., Kang, B., Tokmakov, P., & Wrobel, S. (2013). One click mining: Interactive local pattern discovery through implicit preference and performance learning. In Proceedings of IDEA’13, ACM, New York, NY, pp. 27–35. doi:10.1145/2501511.2501517.
Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge: Cambridge University Press.
Chernoff, H. (1952). A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Annals of Mathematical Statistics, 23, 493–507.
Cover, T. M., & Thomas, J. A. (2012). Elements of information theory. New York: Wiley.
De Bie, T. (2011a). An information theoretic framework for data mining. In Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining (KDD’11) (pp. 564–572).
De Bie, T. (2011b). Maximum entropy models and subjective interestingness: An application to tiles in binary databases. Data Mining and Knowledge Discovery, 23(3), 407–446.
Dzyuba, V., & van Leeuwen, M. (2013). Interactive discovery of interesting subgroup sets. In Advances in intelligent data analysis XII–12th international symposium, IDA 2013, October 17–19, 2013. Proceedings, pp. 150–161. London, UK.
Dzyuba, V., van Leeuwen, M., Nijssen, S., & Raedt, L. D. (2014). Interactive learning of pattern rankings. International Journal on Artificial Intelligence Tools, 23(6), 1460026. doi:10.1142/S0218213014600264.
Fortunato, S., & Barthelemy, M. (2007). Resolution limit in community detection. Proceedings of the National Academy of Sciences, 104(1), 36–41.
Geng, L., & Hamilton, H. J. (2006). Interestingness measures for data mining: A survey. ACM Computing Surveys, 38(3), 9.
Gionis, A., Mannila, H., Mielikäinen, T., & Tsaparas, P. (2007). Assessing data mining results via swap randomization. ACM Transactions on Knowledge Discovery from Data, 1(3), 14.
Goethals, B., Moens, S., & Vreeken, J. (2011). MIME: a framework for interactive visual pattern mining. In Proceedings of KDD’11 (pp. 757–760).
Goldberg, A. V. (1984). Finding a maximum density subgraph. Berkeley, CA: University of California.
Hanhijarvi, S., Ojala, M., Vuokko, N., Puolamäki, K., Tatti, N., & Mannila, H. (2009). Tell me something I don’t know: Randomization strategies for iterative data mining. In Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining (KDD’09) (pp. 379–388).
Hasan, M. A., & Zaki, M. J. (2009). Output space sampling for graph patterns. PVLDB, 2(1), 730–741.
Hoeffding, W. (1963). Probability inequalities for sums of bounded random variables. Journal of the American Statistical Association, 58(301), 13–30.
Kontonasios, K. N., Spyropoulou, E., & De Bie, T. (2012). Knowledge discovery interestingness measures based on unexpectedness. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2(5), 386–399.
McGarry, K. (2005). A survey of interestingness measures for knowledge discovery. Knowledge Engineering Review, 20(1), 39–61.
Newman, M. E., & Girvan, M. (2004). Finding and evaluating community structure in networks. Physical Review E, 69(2), 026,113.
Seidman, S. B. (1983). Network structure and minimum degree. Social Networks, 5(3), 269–287.
Seidman, S. B., & Foster, B. L. (1978). A graph-theoretic generalization of the clique concept. Journal of Mathematical sociology, 6(1), 139–154.
Spyropoulou, E., De Bie, T., & Boley, M. (2014). Mining interesting patterns in multi-relational data. Data Mining and Knowledge Discovery, 28(3), 808–849.
Tsourakakis, C. E., Bonchi, F., Gionis, A., Gullo, F., & Tsiarli, M. A. (2013). Denser than the densest subgraph: Extracting optimal quasi-cliques with quality guarantees. In Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining (KDD’13) (pp. 104–112).
Uno, T. (2010). An efficient algorithm for solving pseudo clique enumeration problem. Algorithmica, 56(1), 3–16.
van Leeuwen, M. (2014). Interactive data exploration using pattern mining. In Interactive knowledge discovery and data mining in biomedical informatics—State-of-the-art and future challenges, LNCS, (vol 8401. pp. 169–182). New York: Springer.
Acknowledgments
We gratefully acknowledge discussions with Jefrey Lijffijt which have helped us to improve the presentation of this manuscript. This work was funded by a Postdoctoral Fellowship of the Research Foundation Flanders (FWO), the European Research Council through the ERC Consolidator Grant FORSIED (Project Reference 615517), and by the EPSRC Project DS4DEMS (EP/M000060/1).
Author information
Authors and Affiliations
Corresponding author
Additional information
Editors: Saso Dzeroski, Dragi Kocev, and Pance Panov.
Appendix: Proof of Theorem 1
Appendix: Proof of Theorem 1
Proof
This follows directly from the Karush–Kuhn–Tucker (KKT) optimality conditions, which for a convex optimization problem with a continuously differentiable objective function and affine constraint functions are both sufficient and necessary (Boyd and Vandenberghe 2004):
The KKT stationarity condition allows us to show that the updated background distribution remains a product of independent Bernoulli distributions. Indeed, using the KKT multipliers \(\lambda _W\ge 0\) for the inequality constraint and \(\mu \in \mathbb {R}\) for the equality constraint, the stationarity condition is given by:
Thus, the following equalities must hold for the minimizer \(P'\):
Slightly reorganising this and with \(Z'=\exp (1-\mu )\) yields the form of the updated background distribution \(P'\):
for constants \(Z'_{u,v}\) with \(Z'=\prod _{u,v\in W, u<v} Z'_{u,v}\).
The other KKT conditions are:
-
Primal feasibility: \(\sum _E P'(E)\phi _W(E)\ge k\) and \(\sum _E P'(E)=1\).
-
Dual feasibility: \(\lambda _W\ge 0\).
-
Complementary slackness: \(\lambda _W\cdot \left( \sum _E P'(E)\phi _W(E)-k\right) = 0\).
The first primal feasibility condition, \(\sum _E P'(E)=1\), requires that the distribution \(P'\) is normalized, which can be achieved by ensuring that all independent factors are normalized, i.e.:
Thus, it follows that:
where
The other KKT conditions yield the value for \(\lambda _W\):
-
If \(\sum _E P(E)\phi _W(E)\ge k\), \(\lambda _W=0\) trivially satisfies all KKT conditions as in that case \(p'_{u,v}=p_{u,v}\) for all \(u,v\in V\) and thus \(P'=P\).
-
Otherwise, for \(\sum _E P(E)\phi _W(E)<k\), the value of \(\lambda _W\) must be such that \(\sum _E P'(E)\phi _W(E)=k\) in order to ensure primal feasibility as well as the complementary slackness condition. From the strict convexity of the problem, it follows that this value for \(\lambda _W\) is unique. To determine it, note that:
$$\begin{aligned} \sum _E P'(E)\phi _W(E)= & {} \sum _{u,v\in W,u<v} \frac{p_{u,v}\cdot \exp (\lambda _W)}{1-p_{u,v}+p_{u,v}\cdot \exp (\lambda _W)}, \end{aligned}$$which is continuous and strictly increasing in \(\lambda _W\). Thus, the unique value for \(\lambda _W\) ensuring that \(\sum _E P'(E)\phi _W(E)=k\) can be found using any one-dimensional root-finding method (such as the bisection method).
\(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
van Leeuwen, M., De Bie, T., Spyropoulou, E. et al. Subjective interestingness of subgraph patterns. Mach Learn 105, 41–75 (2016). https://doi.org/10.1007/s10994-015-5539-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-015-5539-3