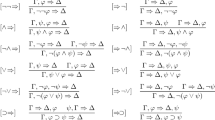Abstract
Belnap and Dunn’s well-known 4-valued logic FDE is an interesting and useful non-classical logic. FDE is defined by using conjunction, disjunction and negation as the sole propositional connectives. Then the question of expanding FDE with an implication connective is of course of great interest. In this sense, some implicative expansions of FDE have been proposed in the literature, among which Brady’s logic BN4 seems to be the preferred option of relevant logicians. The aim of this paper is to define a class of implicative expansions of FDE in whose elements Boolean negation is definable, whence strong logics such as the paraconsistent and paracomplete logic PŁ4 and BN4 itself are definable, in addition to classical propositional logic.
Article PDF
Similar content being viewed by others
References
Anderson, A. R., & Belnap, N. D. (1975). Entailment. The Logic of Relevance and Necessity Vol. I. Princeton: Princeton University Press.
Avron, A. (2020). The normal and self-extensional extension of Dunn–Belnap Logic. Logica Universalis, 14(3), 281–296. https://doi.org/10.1007/s11787-020-00254-1.
Avron, A. (2021). Proof systems for 3-valued logics based on Gödel’s implication. Logic Journal of the IGPL, jzab013. https://doi.org/10.1093/jigpal/jzab013.
Blanco, J. M. (2022). EF4, EF4-M and EF4-Ł: A companion to BN4 and two modal four-valued systems without strong Łukasiewicz-type modal paradoxes. Logic and Logical Philosophy, 31(1), 75–104. https://doi.org/10.12775/LLP.2021.010.
Belnap Jr, N. D. (1977a). In Epstein, G., Dunn, J. M., Belnap Jr, N. D., & Reidel D. (Eds.), A useful four-valued logic, (pp. 8–37). Dordrecht: Publishing Co.
Belnap Jr, N. D. (1977b). In Ryle, G., & Belnap Jr, N. D. (Eds.), How a computer should think, (pp. 30–55). Stocksfield: Oriel Press Ltd.
Brady, R. T. (1982). Completeness proofs for the systems RM3 and BN4. Logique et Analyse, 25(97), 9–32.
Brady, R. T. (Ed.) (2003). Relevant logics and their rivals, vol II. Aldershot: Ashgate.
Brady, R. T. (2006). Universal logic CSLI. Stanford, CA.
Carnielli, W., Marcos, J., & Amo, S. D. E. (2000). Formal inconsistency and evolutionary databases. Logic and Logical Philosophy, 8, 115–152. https://doi.org/10.12775/LLP.2000.008.
De, M., & Omori, H. (2015). Classical negation and expansions of Belnap–Dunn logic. Studia Logica, 103(4), 825–851. https://doi.org/10.1007/s11225-014-9595-7.
Dunn, J. M. (1966). The algebra of intensional logics. In PhD Thesis. University of Pittsburgh. UMI, Ann Arbor, MI. (Published as vol. 2 in the Logic PhDs series by College Publications, London, UK, 2019.
Dunn, J. M. (1976). Intuitive semantics for first-degree entailments and “coupled trees.” Philosophical Studies, 29, 149–168.
Dunn, J. M. (2000). Partiality and its dual. Studia Logica, 66(1), 5–40. https://doi.org/10.1023/A:1026740726955.
González, C. (2011). MaTest, v. 1.3.2a. https://sites.google.com/site/sefusmendez/matest. Last Accessed 29 Apr 2022.
Kamide, N., & Omori, H. (2017). An extended first-order Belnap-Dunn logic with classical negation. In A. Baltag, J. Seligman, & Yamada T. (Eds.) Logic, Rationality, and Interaction: Lecture Notes in Computer Science, vol. 10455 (pp. 79–93). Springer, Berlin, Heidelbereg. https://doi.org/10.1007/978-3-662-55665-8_6.
Karpenko, A. S. (1999). Jaśkowski’s criterion and three-valued paraconsistent logics. Logic and Logical Philosophy, 7, 81–86. https://doi.org/10.12775/LLP.1999.006.
López Velasco, S. M. (2020). Estudio sobre las variantes de la matriz tetravaluada de Brady que verifican la lógica básica de Routley y Meyer. PhD thesis Universidad de Salamanca, Salamanca, Spain.
López, S. M. (2022). Belnap-Dunn semantics for the variants of BN4 and E4 which contain Routley and Meyer’s logic B. Logic and Logical Philosophy, 31(1), 29–56. https://doi.org/10.12775/LLP.2021.004.
Łukasiewicz, J., & Tarski, A. (1930). Untersuchungen über den Aussagenkalkül. Comptes Rendus des Séances de la Société des Sciences et des Lettres de Varsovie, Classe, III(23), 30–50.
Méndez, J. M., & Robles, G. (2015). A strong and rich 4-valued modal logic without Łukasiewicz-type paradoxes. Logica Universalis, 9(4), 501—522. https://doi.org/10.1007/s11787-015-0130-z.
Méndez, J. M., & Robles, G. (2016a). The logic determined by Smiley’s matrix for Anderson and Belnap’s first-degree entailment logic. Journal of Applied Non-Classical Logics, 26(1), 47–68. https://doi.org/10.1080/11663081.2016.1153930.
Méndez, J. M., & Robles, G. (2016b). Strengthening Brady’s paraconsistent 4-valued logic BN4 with truth-functional modal operators. Journal of Logic Language and Information, 25(2), 163–189. https://doi.org/10.1007/s10849-016-9237-8.
Meyer, R. K., Giambrone, S., & Brady, R. T. (1984). Where gamma fails. Studia Logica, 43, 247–256. https://doi.org/10.1007/BF02429841.
Omori, H., & Wansing, H. (2017). 40 years of FDE: An introductory overview. Studia Logica, 10(6), 1021–1049. https://doi.org/10.1007/s11225-017-9748-6.
Omori, H. & Wansing H. (Eds.) (2019). New essays on Belnap-Dunn logic. Synthese Library (Stud ies in Epistemology, Logic, Methodology, and Philosophy of Science). (Vol. 418). Cham: Springer. https://doi.org/10.1007/978-3-030-31136-0.
Petrukhin, Y., & Shangin, V. (2020). Correspondence analysis and automated proof-searching for first degree entailment. European Journal of Mathematics, 6(4), 1452–1495. https://doi.org/10.1007/s40879-019-00344-5.
Robles, G., & Méndez, J. M. (2016). A companion to Brady’s 4-valued relevant logic BN4: The 4-valued logic of entailment E4. Logic Journal of the IGPL, 24 (5), 838–858. https://doi.org/10.1093/jigpal/jzw011.
Robles, G., & Méndez, J. M. (2019). Belnap-Dunn semantics for natural implicative expansions of Kleene’s strong three-valued matrix with two designated values. Journal of Applied Non-Classical Logics, 29(1), 37–63. https://doi.org/10.1080/11663081.2018.1534487.
Robles, G., & Méndez, J. M. (2020). The class of all natural implicative expansions of Kleene’s strong logic functionally equivalent to Łukasiewicz’s 3-valued logic Ł3. Journal of Logic Language and Information, 29(3), 349–374. https://doi.org/10.1007/s10849-019-09306-2.
Robles, G., & Méndez, J. M. (2022a). A remark on functional completeness of binary expansions of Kleene’s strong 3-valued logic. Logic Journal of the IGPL, 30(1), 21–33. https://doi.org/10.1093/jigpal/jzaa028.
Robles, G., & Méndez J. M. (2022b). A 2 set-up Routley-Meyer semantics for the 4-valued logic PŁ4. Journal of Applied Logics — IfCoLog Journal of Logics and their Applications, 8(10), 2435–2446.
Robles, G., & Méndez, J. M. (2022c). A note on functional relations in a certain class of implicative expansions of FDE related to Brady’s 4-valued logic BN4. Logic Journal of the IGPL, jzac045, 1–8. https://doi.org/10.1093/jigpal/jzac045.
Routley, R., Meyer, R. K., Plumwood, V., & Brady R. T. (1982). Relevant logics and their rivals, vol. 1. Atascadero, CA, Ridgeview Publishing Co.
Slaney, J. (2005). Relevant logic and paraconsistency. In L. Bertossi, A. Hunter, & T. Schaub (Eds.) Inconsistency Tolerance, Lecture Notes in Computer Science, vol. 3300 (pp. 270–293). Berlin: Springer, DOI https://doi.org/10.1007/978-3-540-30597-2_9, (to appear in print).
Acknowledgements
We sincerely thank two anonymous referees of the Journal of Philosophical Logic for their comments and suggestion on a previous draft of this paper. - This work is funded by the Spanish Ministry of Science and Innovation (MCIN/AEI/ 10.13039/501100011033) under Grant [PID2020-116502GB-I00].
Funding
The authors declare that this work is funded by the Spanish Ministry of Science and Innovation (MCIN/AEI/ 10.13039/501100011033) (Grant number [PID2020-116502GB-I00]).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare there are no competing interests.
Financial interests
The authors declare that they have no financial interests.
Non-financial interests
The authors declare that they have no financial interests. The authors declare that they have no non-financial interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Robles, G., Méndez, J.M. A Class of Implicative Expansions of Belnap-Dunn Logic in which Boolean Negation is Definable. J Philos Logic 52, 915–938 (2023). https://doi.org/10.1007/s10992-022-09692-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-022-09692-2