Abstract
Epistemic closure has been a central issue in epistemology over the last forty years. According to versions of the relevant alternatives and subjunctivist theories of knowledge, epistemic closure can fail: an agent who knows some propositions can fail to know a logical consequence of those propositions, even if the agent explicitly believes the consequence (having “competently deduced” it from the known propositions). In this sense, the claim that epistemic closure can fail must be distinguished from the fact that agents do not always believe, let alone know, the consequences of what they know—a fact that raises the “problem of logical omniscience” that has been central in epistemic logic. This paper, part I of II, is a study of epistemic closure from the perspective of epistemic logic. First, I introduce models for epistemic logic, based on Lewis’s models for counterfactuals, that correspond closely to the pictures of the relevant alternatives and subjunctivist theories of knowledge in epistemology. Second, I give an exact characterization of the closure properties of knowledge according to these theories, as formalized. Finally, I consider the relation between closure and higher-order knowledge. The philosophical repercussions of these results and results from part II, which prompt a reassessment of the issue of closure in epistemology, are discussed further in companion papers. As a contribution to modal logic, this paper demonstrates an alternative approach to proving modal completeness theorems, without the standard canonical model construction. By “modal decomposition” I obtain completeness and other results for two non-normal modal logics with respect to new semantics. One of these logics, dubbed the logic of ranked relevant alternatives, appears not to have been previously identified in the modal logic literature. More broadly, the paper presents epistemology as a rich area for logical study.
Similar content being viewed by others
1 Introduction
The debate over epistemic closure has been called “one of the most significant disputes in epistemology over the last forty years” [45, 256]. The starting point of the debate is typically some version of the claim that knowledge is closed under known implication (see Dretske [22]). At its simplest, it is the claim that if an agent knows φ and knows that φ implies ψ, then the agent knows ψ: (Kφ ∧ K (φ ⇾ ψ)) ⇾ Kψ, in the language of epistemic logic.
An obvious objection to the simple version of the claim is that an agent with bounded rationality may know φ and know that φ implies ψ, yet not “put two and two together” and draw a conclusion about ψ. Such an agent may not even believe ψ, let alone know it. The challenge of the much-discussed “problem of logical omniscience” (see, e.g., Stalnaker [69]; Halpern and Pucella [29]) is to develop a good theoretical model of the knowledge of such agents.
According to a different objection, made famous in epistemology by Dretske [19] and Nozick [58] (and applicable to more sophisticated closure claims), knowledge would not be closed under known implication even for “ideally astute logicians” [19, 1010] who always put two and two together and believe all consequences of what they believe. This objection (explained in Section 2), rather than the logical omniscience problem, will be our starting point.Footnote 1
The closure of knowledge under known implication, henceforth referred to as ‘K’ after the modal axiom given above, is one closure principle among infinitely many. Although Dretske [19] denied K, he accepted other closure principles, such as closure under conjunction elimination, K (φ ∧ ψ) → Kφ, and closure under disjunction introduction, Kφ → K (φ ∨ ψ) (1009). By contrast, Nozick [58] was prepared to give up closure under conjunction elimination (228), although not closure under disjunction introduction (230n64, 692).
Dretske and Nozick not only provided examples in which they claimed K fails, but also proposed theories of knowledge that they claimed would explain the failures, as discussed below. Given such a theory, one may ask: is the theory committed to the failure of other, weaker closure principles, such as those mentioned above? Is it committed to closure failures in situations other than those originally envisioned as counterexamples to K? The concern is that closure failures may spread, and they may spread to where no one wants them.
Pressing such a problem of containment has an advantage over other approaches to the debate over K. It appeals to considerations that both sides of the debate are likely to accept, rather than merely insisting on the plausibility of K (or of one of its more sophisticated versions). A clear illustration of this approach is Kripke’s [44] barrage of arguments to the effect that closure failures are ubiquitous given Nozick’s theory of knowledge. In a different way, Hawthorne [32, 41] presses the first part of the containment problem against Dretske and Nozick, as I critically discuss in Holliday [38, Section 6.1.2].Footnote 2
In this paper, I formally assess the problem of containment for a family of prominent “modal” theories of knowledge (see, e.g., Pritchard [61]; Black [9]). In particular, I introduce formal models of the following: the relevant alternatives (RA) theories of Lewis [52] and Heller [33, 34]; one way of developing the RA theory of Dretske [21] (based on Heller); the basic tracking theory of Nozick [58]; and the basic safety theory of Sosa [67]. A common feature of the theories of Heller, Nozick, and Sosa, which they share with those of Dretske [20], Goldman [26], and others, is some subjunctive or counterfactual-like condition(s) on knowledge, relating what an agent knows to what holds in selected counterfactual possibilities or epistemic alternatives.
Vogel [76] characterizes subjunctivism as “the doctrine that what is distinctive about knowledge is essentially modal in character, and thus is captured by certain subjunctive conditionals” (73), and some versions of the RA theory have a similar flavor.Footnote 3 I will call this family of theories subjunctivist flavored. Reflecting their commonality, my formal framework is based on the formal semantics for subjunctive conditionals in the style of Lewis [49] and Stalnaker [68]. As a result, the epistemic logics studied here behave very differently than traditional epistemic logics in the style of Hintikka [36]. (For a philosophically-oriented review of basic epistemic logic, see Holliday [39]).
This paper is part I of II. The main result of part I is an exact characterization in propositional epistemic logic of the closure properties of knowledge according to the RA, tracking, and safety theories, as formalized. Below I preview some of the epistemological and logical highlights of this and other results from part I. Part II introduces a unifying framework in which all of the theories of knowledge studied here fit as special cases; I argue that the closure problems with these theories are symptoms of inherent problems in their framework; and I propose to solve these problems with a new framework for fallibilist theories of knowledge. Elsewhere I discuss the philosophical repercussions of the results from parts I and II in depth [38, 40].
Epistemological Points
The extent to which subjunctivist-flavored theories of knowledge preserve closure has recently been a topic of active discussion (see, e.g., Alspector-Kelly [3]; Adams et al. [1]). I show (in Section 5) that in contrast to Lewis’s (non-subjunctive) theory, the other RA, tracking, and safety theories cited suffer from essentially the same widespread closure failures, far beyond the failure of K, which few if any proponents of these theories would welcome.Footnote 4 The theories’ structural features responsible for these closure failures also lead (in Section 8) to serious problems of higher-order knowledge, including the possibility of knowing Fitch-paradoxical propositions [23].
Analysis of these results reveals (in Section 9) that two parameters of a modal theory of knowledge affect whether it preserves closure. Each parameter has two values, for four possible parameter settings with respect to which each theory can be classified (Table 2). Of the theories mentioned, only Lewis’s, with its unique parameter setting, fully preserves closure (for a fixed context). (In Section 8 I clarify an issue, raised by Williamson [79, 80], about whether Lewis’s theory also validates strong principles of higher-order knowledge).
In the terminology of Dretske [19], the knowledge operator for Lewis’s theory is fully penetrating. For all of the other theories, the knowledge operator lacks the basic closure properties that Dretske wanted from a semi-penetrating operator. Contrary to common assumptions in the literature (perhaps due to neglect of the second theory parameter in Section 9), serious closure failures are not avoided by modified subjunctivist theories, such as DeRose’s [17] modified tracking theory or the modified safety theory with bases, treated formally in Holliday [38, Sections 2.10.1, 2.D]. For those seeking a balance of closure properties between full closure and not enough closure, it appears necessary to abandon essential elements of the standard theories. I show how to do so in part II.
While I take the results of this paper to be negative for subjunctivist-flavored theories qua theories of knowledge, we can also take them to be neutral results about other desirable epistemic properties, viz., the properties of having ruled out the relevant alternatives to a proposition, of having a belief that tracks the truth of a proposition, of having a safe belief in a proposition, etc., even if these are neither necessary nor sufficient for knowledge (see Sections 5 and 7).
Logical Points
This paper demonstrates the effectiveness of an alternative approach to proving modal completeness theorems, illustrated by van Benthem [8, Section 4.3] for the normal modal logic K, in a case that presents difficulties for a standard canonical model construction. The key element of the alternative approach is a “modal decomposition” result. By proving such results (Theorem 5.2), we will obtain completeness (Corollary 7.1) of two non-normal modal logics with respect to new semantics mixing elements of ordering semantics [50] and relational semantics [43]. One of these logics, dubbed the logic of ranked relevant alternatives, appears not to have been previously identified in the modal logic literature. Further results on decidability (Corollary 5.9), finite models (Corollary 5.24), and complexity (Corollary 5.25) follow from the proof of the modal decomposition results.
In addition to these technical points, the paper aims to show that for modal logicians, epistemology represents an area of sophisticated theorizing in which modal-logical tools can help to clarify and systematize parts of the philosophical landscape. Doing so also benefits modal logic by broadening its scope, bringing interesting new structures and systems under its purview.
In Section 2, I begin with our running example, motivating the issue of epistemic closure. I then introduce the formal framework for the study of closure in RA and subjunctivist theories in Sections 3 and 4. With this setup, I state and prove the main theorems in Sections 5 and 7, with an interlude on relations between RA and subjunctivist models in Section 6. Finally, I investigate higher-order knowledge in Section 8 and discuss the relation between theory parameters and closure failures in Section 9.
Throughout the paper, comments on the faithfulness of the formalization to the philosophical ideas are often in order. To avoid disrupting the flow of presentation, I place some of these important comments in footnotes. Readers who wish to focus on logical ideas should be able to step from definitions to lemmas to theorems, reading the exposition between steps as necessary.
2 The Question of Closure
Example 2.1 (Medical Diagnosis)
Two medical students, A and B, are subjected to a test. Their professor introduces them to the same patient, who presents various symptoms, and the students are to make a diagnosis of the patient’s condition. After some independent investigation, both students conclude that the patient has a common condition c. In fact, they are both correct. Yet only student A passes the test. For the professor wished to see if the students would check for another common condition c′ that causes the same visible symptoms as c. While A ran laboratory tests to rule out c′ before making the diagnosis of c, B made the diagnosis of c after only a physical exam.
In evaluating the students, the professor concludes that although both gave the correct diagnosis of c, student B did not know that the patient’s condition was c, since B did not rule out the alternative of c′. Had the patient’s condition been c′, student B would (or at least might) still have thought it was c, since the physical exam would not have revealed a difference. Student B was lucky. The condition that B associated with the patient’s visible symptoms happened to be what the patient had, but if the professor had chosen a patient with c′, student B might have made a misdiagnosis. By contrast, student A secured against this possibility of error by running the lab tests. For this reason, the professor judges that student A knew the patient’s condition, passing the test.
Of course, A did not secure against every possibility of error. Suppose there is an extremely rare diseaseFootnote 5 x such that people with x appear to have c on lab tests given for c and c′, even though people with x are immune to c, and only extensive further testing can detect x in its early stages. Should we say that A did not know that the patient had c after all, since A did not rule out x? According to a classic relevant alternatives style answer (see Goldman [26, 775]; Dretske [21, 365]), the requirement that one rule out all possibilities of error would make knowledge impossible, since there are always some possibilities of error—however remote and far-fetched—that are not eliminated by one’s evidence and experience. Yet if no one had any special reason to think that the patient may have had x instead of c, then it should not have been necessary to rule out such a remote possibility in order to know that the patient has the common condition (cf. Austin [5, 156ff]; Stroud [71, 51ff]).Footnote 6
If one accepts the foregoing reasoning, then one is close to denying closure under known implication (K). For suppose that student A knows that if her patient has c, then he does not have x (because x confers immunity to c), (i) K (c → ¬x).Footnote 7 Since A did not run any of the tests that could detect the presence or absence of x, arguably she does not know that the patient does not have x, (ii) ¬K ¬x. Given the professor’s judgment that A knows that the patient has condition c, (iii) Kc, together (i)–(iii) violate the following instance of K: (iv) (Kc ∧ K (c → ¬x)) → K ¬x. To retain K, one must say either that A does not know that the patient has condition c after all (having not excluded x), or else that A can know that a patient does not have a disease x without running any of the specialized tests for the disease (having learned instead that the patient has c, but from lab results consistent with x).Footnote 8 While the second option threatens to commit us to problematic “easy knowledge” [14], the first option threatens to commit us to radical skepticism about knowledge, given the inevitability of uneliminated possibilities of error noted above.
Dretske [19] and Nozick [58] propose to resolve the inconsistency of (i)–(iv), a version of the now standard “skeptical paradox” [13, 17], by denying the validity of K and its instance (iv) in particular. This denial has nothing to do with the “putting two and two together” problem noted in Section 1. The claim is that K would fail even for Dretske’s [19] “ideally astute logicians” (1010). I will cash out this phrase as follows: first, such an agent knows all (classically) valid logical principles (validity omniscience);Footnote 9 second, such an agent believes all the (classical) logical consequences of the set of propositions she believes (full doxastic closure).Footnote 10 Dretske’s explanation for why K fails even for such agents is in terms of the RA theory. (We turn to Nozick’s view in Section 4). For this theory, to know p is (to truly believe p and) to have ruled out the relevant alternatives to p. In coming to know c and → ¬x, the agent rules out certain relevant alternatives. In order to know ¬x, the agent must rule out certain relevant alternatives. But the relevant alternatives in the two cases are not the same. According to our earlier reasoning, x is not an alternative that must be ruled out in order for Kc to hold. But x is an alternative that must be ruled out in order for K ¬x to hold (cf. Remark 3.9 in Section 3). It is because the relevant alternatives may be different for what is in the antecedent and the consequent of K that instances like (iv) can fail.
In an influential objection to Dretske, Stine [70] claimed that to allow for the relevant alternatives to be different for the premises and conclusion of an argument about knowledge “would be to commit some logical sin akin to equivocation” (256). Yet as Heller [34] points out in Dretske’s defence, a similar charge of equivocation could be made (incorrectly) against accepted counterexamples to the principles of transitivity or antecedent strengthening for counterfactuals. If we take a counterfactual φ □→ ψ to be true iff the “closest” φ-worlds are ψ-worlds, then the inference from φ □→ ψ to (φ ∧ χ) □→ ψ is invalid because the closest (φ ∧ χ)-worlds may not be among the closest φ-worlds. Heller argues that there is no equivocation in such counterexamples since we use the same, fixed similarity ordering of worlds to evaluate the different conditionals. Similarly, in the example of closure failure, the most relevant ¬c-worlds may differ from the most relevant x-worlds—so one can rule out the former without ruling out the latter—even assuming a fixed relevance ordering of worlds. In this defense of Dretske, Heller brings the RA theory closer to subjunctivist theories that place counterfactual conditions on knowledge.
With this background, let us formulate the question of closure to be studied. We begin with the official definition of our (first) propositional epistemic language. The framework of Sections 3 and 4 could be extended for quantified epistemic logic, but there is already plenty to investigate in the propositional case.Footnote 11
Definition 2.2 (Epistemic Language)
Let At = {p, q, r, …} be a countably infinite set of atomic sentences. The epistemic language is defined inductively by
where p ∈ At. As usual, expressions containing ∨, → , and ↔ are abbreviations, and by convention ∧ and ∨ bind more strongly than → or ↔ in the absence of parentheses; we take ⊤ to be an arbitrary tautology (e.g., p ∨ ¬p), and ⊥ to be ¬⊤. The modal depth of a formula φ is defined recursively as follows: d (p) = 0, d(¬φ) = d(φ), d(φ ∧ ψ) = max (d(φ), d(ψ)), and d(Kφ) = d(φ) + 1. A formula φ is propositional iff d(φ) = 0 and flat iff d(φ) ≤ 1.
The flat fragment of the epistemic language has a special place in the study of closure, which need not involve higher-order knowledge. In the most basic case we are interested in whether for a valid propositional formula φ 1 ∧ ⋯ ∧ φ n → ψ, the associated “closure principle” Kφ 1 ∧ ⋯ ∧ Kφ n → Kψ is valid, according to some semantics for the K operator. More generally, we will consider closure principles of the form Kφ 1 ∧ ⋯ ∧ Kφ n → Kψ 1 ∨ ⋯ ∨ Kψ m , allowing each φ i and ψ j to be of arbitrary modal depth. As above, we ask whether such principles hold for ideally astute logicians. The question can be understood in several ways, depending on whether we have in mind what may be called pure, empirical, or deductive closure principles.
Remark 2.3 (Types of Closure)
For example, if we understand the principle K(φ ∧ ψ) → Kψ as a pure closure principle, then its validity means that an agent cannot know φ ∧ ψ without knowing ψ—regardless of whether the agent came to believe ψ by “competent deduction” from φ ∧ ψ.Footnote 12 (Perhaps she came to believe ψ from perception, φ from testimony, and φ ∧ ψ by competent deduction from φ and ψ.) More generally, if we understand Kφ 1 ∧ ⋯ ∧ Kφ n ⇾ Kψ as a pure closure principle, its validity means that an agent cannot know φ 1, …, φ n without knowing ψ. Understood as an empirical closure principle, its validity means that an agent who has done enough empirical investigation to know φ 1, …, φ n has done enough to know ψ. Finally, understood as a deductive closure principle, its validity means that if the agent came to believe ψ from φ 1, …, φ n by competent deduction, all the while knowing φ 1, …, φ n , then she knows ψ. As suggested by Williamson [78, 282f], it is highly plausible that K(φ ∧ ψ) → Kψ is a pure (and hence empirical and deductive) closure principle. By contrast, closure under known implication is typically understood as only an empirical or deductive closure principle.Footnote 13 Here we will not explicitly represent in our language or models the idea of deductive closure. I do so elsewhere [38, Section 2.D] in formalizing versions of the tracking and safety theories that take into account methods or bases of beliefs. It is first necessary to understand the structural reasons for why the basic RA, tracking, and safety conditions are not purely or empirically closed, in order to understand whether the refined theories solve all the problems of epistemic closure.Footnote 14
3 Relevant Alternatives
In this section, I introduce formalizations of two RA theories of knowledge. Before giving RA semantics for the epistemic language of Definition 2.2, let us observe several distinctions between different versions of the RA theory.
The first concerns the nature of the “alternatives” that one must rule out to know p. Are they possibilities (or ways the world could/might be) in which p is false?Footnote 15 Or are they propositions incompatible with p? Both views are common in the literature, sometimes within a single author. Although earlier I wrote in a way suggestive of the second view, in what follows I adopt the first view, familiar in the epistemic logic tradition since Hintikka, since it fits the theories I will formalize. For a comparison of the views, see Holliday [38, Section 4.A].
The second distinction concerns the structure of relevant alternatives. On one hand, Dretske [21] states the following definition in developing his RA theory: “call the set of possible alternatives that a person must be in an evidential position to exclude (when he knows P) the Relevancy Set (RS)” (371). On the other hand, Heller [34] considers (and rejects) an interpretation of the RA theory in which “there is a certain set of worlds selected as relevant, and S must be able to rule out the not-p worlds within that set” (197).
According to Dretske, for every proposition P, there is a relevancy set for that P. Let us translate this into Heller’s talk of worlds. Where \(\overline {P}\) is the set of all worlds in which P is false, let r (P) be the relevancy set for P, so \(\mathsf {r}(P)\subseteq \overline {P}\). To be more precise, since objective features of an agent’s situation in world w may affect what alternatives are relevant and therefore what it takes to know P in w (see Dretske [21, 377] and DeRose [18, 30f] on “subject factors”), let us write ‘r(P, w)’ for the relevancy set for P in world w, so r(P, w) may differ from r(P, v) for a distinct world v in which the agent’s situation is different. Finally, if we allow (unlike Dretske) that the conversational context 𝒞 of those attributing knowledge to the agent can also affect what alternatives are relevant in a given situation w and therefore what it takes to count as knowing P in w relative to 𝒞 (see [18, 30f] on “attributor factors”), then we should write ‘r 𝒞 (P, w)’ to make the relativization to context explicit.
The quote from Dretske suggests the following definition:
According to a RS ∀∃ theory, for every context 𝒞, for every world w, and for every (∀) proposition P, there is (∃) a set of relevant (in w) not-P worlds, \(\mathsf {r}_{_{\mathcal {C}}}(P,w)\subseteq \overline {P}\), such that in order to know P in w (relative to 𝒞) one must rule out the worlds in \(\mathsf {r}_{_{\mathcal {C}}}(P,w)\).
By contrast, the quote from Heller suggests the following definition:
According to a RS ∃∀ theory, for every context 𝒞 and for every world w, there is (∃) a set of relevant (in w) worlds, R 𝒞 (w), such that for every (∀) proposition P, in order to know P in w (relative to 𝒞) one must rule out the not-P worlds in that set, i.e., the worlds in \(\mathsf {R}_{_{\mathcal {C}}}(w)\cap \overline {P}\).
As a simple logical observation, every RS ∃∀ theory is a RS ∀∃ theory (take \(\mathsf {r}_{_{\mathcal {C}}}(P,w)=\mathsf {R}_{_{\mathcal {C}}}(w)\cap \overline {P}\)), but not necessarily vice versa. From now on, when I refer to RS ∀∃ theories, I have in mind theories that are not also RS ∃∀ theories. This distinction is at the heart of the disagreement about epistemic closure between Dretske and Lewis [52], as Lewis clearly adopts an RS ∃∀ theory.
In a contextualist RS ∃∀ theory, such as Lewis’s, the set of relevant worlds may change as context changes. Still, for any given context 𝒞, there is a set R 𝒞 (w) of relevant (at w) worlds, which does not depend on the particular proposition in question. The RS ∀∃ vs. RS ∃∀ distinction is about how theories view the relevant alternatives with respect to a fixed context. Here we study which closure principles hold for different theories with respect to a fixed context. Elsewhere I extend the framework to context change [37, 38].
A third distinction between versions of the RA theory concerns different notions of ruling out or eliminating alternatives (possibilities or propositions). On one hand, Lewis [52] proposes that “a possibility …[v] …is uneliminated iff the subject’s perceptual experience and memory in …[v] …exactly match his perceptual experience and memory in actuality” (553). On the other hand, Heller [34] proposes that “S’s ability to rule out not-p be understood thus: S does not believe p in any of the relevant not-p worlds” (98). First, we model the RA theory with a Lewis-style notion of elimination. By ‘Lewis-style’, I do not mean a notion that involves experience or memory; I mean any notion of elimination that allows us to decide whether a possibility v is eliminated by an agent in w independently of any proposition P under consideration, as Lewis’s notion does. In Section 4, we turn to Heller’s notion, which is closely related to Nozick’s [58] tracking theory. We compare the two notions in Section 9.
Below we define our first class of models, following Heller’s RA picture of “worlds surrounding the actual world ordered according to how realistic they are, so that those worlds that are more realistic are closer to the actual world than the less realistic ones” [33, 25] with “those that are too far away from the actual world being irrelevant” [34, 199]. These models represent the epistemic state of an agent from a third-person perspective. We should not assume that anything in the model is something that the agent has in mind. Contextualists should think of the model ℳ as associated with a fixed context of knowledge attribution, so a change in context corresponds to a change in models from ℳ to ℳ′ (an idea formalized in Holliday [37, 38]). Just as the model is not something that the agent has in mind, it is not something that particular speakers attributing knowledge to the agent have in mind either. For possibilities may be relevant and hence should be included in our model, even if the attributors are not considering them (see DeRose [18, 33]).
Finally, for simplicity (and in line with Lewis [52]) we will not represent in our RA models an agent’s beliefs separately from her knowledge. Adding the doxastic machinery of Section 4 (which guarantees doxastic closure) would be easy, but if the only point were to add believing φ as a necessary condition for knowing φ, this would not change any of our results about RA knowledge.Footnote 16
Definition 3.1 (RA Model)
A relevant alternatives model is a tuple ℳ of the form 〈W, ⇾, ≤, V〉 where:
-
1.
W is a nonempty set;
-
2.
⇾ is a reflexive binary relation on W ;
-
3.
≤ assigns to each w ∈ W a binary relation ≤ w on some W w ⊆ W;
-
(a)
≤ w is reflexive and transitive;
-
(b)
w ∈ W w , and for all v ∈ W w , w ≤ w v;
-
(a)
-
4.
V assigns to each p ∈ At a set V (p) ⊆ W.
For w ∈ W, the pair ℳ, w is a pointed model.
I refer to elements of W as “worlds” or “possibilities” interchangeably.Footnote 17 As usual, think of V (p) as the set of worlds where the atomic sentence p holds.
Take w ⇾ v to mean that v is an uneliminated possibility for the agent in w.Footnote 18 For generality, I assume only that ⇾ is reflexive, reflecting the fact that an agent can never eliminate her actual world as a possibility. According to Lewis’s [52] notion of elimination, ⇾ is an equivalence relation. However, whether we assume transitivity and symmetry in addition to reflexivity does not affect our main results (see Remark 5.20). This choice only matters if we make further assumptions about the ≤ w relations, discussed in Section 8.
Take u ≤ w v to mean that u is at least as relevant (at w) as v is.Footnote 19 A relation satisfying Definition 3.1.3a is a preorder. The family of preorders in an RA model is like one of Lewis’s (weakly centered) comparative similarity systems [49, Section 2.3] or standard γ-models [48], but without his assumption that each ≤ w is total on its field W w (see Def. 3.3.3). Condition 3b, that w is at least as relevant at w as any other world is, corresponds to Lewis’s [52] Rule of Actuality, that “actuality is always a relevant alternative” (554).
By allowing ≤ w and ≤ v to be different for distinct worlds w and v, we allow the world-relativity of comparative relevance (based on differences in “subject factors”) discussed above. A fixed context may help to determine not only which possibilities are relevant, given the way things actually are, but also which possibilities would be relevant were things different. Importantly, we also allow ≤ w and ≤ v to be different when v is an uneliminated possibility for the agent in w, so w ⇾ v. In other words, we do not assume that in w the agent can eliminate any v for which ≤ v ≠ ≤ w . As Lewis [52] put it, “the subject himself may not be able to tell what is properly ignored” (554). We will return to these points in Section 8 in our discussion of higher-order knowledge.
Notation 3.2 (Derived Relations, Min)
Where w, v, u ∈ W and S ⊆ W,
-
u ≺ w v iff u ≤ w v and not v ≤ w u; and u ≃ w v iff u ≤ w v and v ≤ w u;
-
\(\text {Min}_{\preceq _{w}}\) (S) = {v ∈ S ∩ W w ∣ there is no u ∈ S such that u ≺ w v}.
Hence u ≺ w v means that possibility u is more relevant (at w) than possibility v is, while u ≃ w v means that they are equally relevant. \(\text {Min}_{\preceq _{w}}(S)\) is the set of most relevant (at w) possibilities out of those in S that are ordered by ≤ w , in the sense that there are no other possibilities that are more relevant (at w).
Definition 3.3 (Types of Orderings)
Consider an RA model ℳ = 〈W, ⇾, ≤, V〉 with w ∈ W.
-
1.
≤ w is well-founded iff for every nonempty S ⊆ W w , \(\text {Min}_{\preceq _{w}}(S)\not =\emptyset \);
-
2.
≤ w is linear iff for all u, v ∈ W w , either u ≺ w , v, v ≺ w u, or u = v;
-
3.
≤ w is total iff for all u, v ∈ W w , u ≤ w v or v ≤ w u;
-
4.
≤ w has a universal field iff W w = W;
-
5.
≤ w is centered (weakly centered) iff \(\text {Min}_{\preceq _{w}}(W)=\{w\}\) (\(w\in \text {Min}_{\preceq _{w}}(W)\)).
If a property holds of ≤ v for all v ∈ W, then we say that ℳ has the property.
Well-foundedness is a (language-independent) version of the “Limit Assumption” discussed by Lewis [49, Section 1.4]. Together well-foundedness and linearity amount to “Stalnaker’s Assumption” (ibid., Section 3.4). Totality says that any worlds in the field of ≤ w are comparable in relevance. So a total preorder ≤ w is a relevance ranking of worlds in W w . Universality (ibid., Section 5.1) says that all worlds are assessed for relevance at w. Finally, (with Def. 3.1.3b) centering (ibid., Section 1.3) says that w is the most relevant world at w, while weak centering (ibid., Section 1.7) (implied by Def. 3.1.3b) says that w is among the most relevant.
I assume well-foundedness (always satisfied in finite models) in what follows, since it allows us to state more perspicuous truth definitions. However, this assumption does not affect our results (see Remark 5.13). By contrast, totality does make a difference in valid closure principles for one of our theories (see Fact 5.7), while the addition of universality does not (see Prop. 5.23). I comment on linearity and centering vs. weak centering after Definition 3.6.
We now interpret the epistemic language of Definition 2.2 in RA models, considering three semantics for the K operator. I call these C-semantics, for Cartesian, D-semantics, for Dretske, and L-semantics, for Lewis. C-semantics is not intended to capture Descartes’ view of knowledge. Rather, it is supposed to reflect a high standard for the truth of knowledge claims—knowledge requires ruling out all possibilities of error, however remote—in the spirit of Descartes’ worries about error in the First Meditation; formally, C-semantics is just the standard semantics for epistemic logic in the tradition of Hintikka [36], but I reserve ‘H-semantics’ for later. D-semantics is one way (but not the only way) of understanding Dretske’s [21] RS ∀∃ theory, using Heller’s [33, 34] picture of relevance orderings over possibilities.Footnote 20 Finally, L-semantics follows Lewis’s [52] RS ∃∀ theory (for a fixed context).
Definition 3.4 (Truth in an RA Model)
Given a well-founded RA model ℳ = 〈W, ⇾, ≤, V〉 with w ∈ W and a formula φ in the epistemic language, define ℳ, w ⊨ x φ (φ is true at w in ℳ according to X-semantics) as follows:
For the K operator, the C-semantics clause is that of standard modal logic:

which states that φ is known at w iff φ is true in all possibilities uneliminated at w. I will write this clause in another, equivalent way below, for comparison with the D- and L-semantics clauses. First, we need two pieces of notation.
Notation 3.5 (Extension and Complement)
Where ℳ = 〈W, ⇾, ≤, V〉,
-
\(\left[\left[ \varphi \right]\right] _{x}^{\mathcal {M}}=\left\{ v\in W\mid \mathcal {M},v\vDash _{x}\varphi \right \} \) is the set of worlds where φ is true in ℳ according to X-semantics; if ℳ and x are clear from context, I write ‘⟦φ⟧’.
-
For S ⊆ W, S̅ = {v ∈ W ∣ v ∉ S} is the complement of S in W. When W may not be clear from context, I write ‘W ∖ S’ instead of ‘S̅’.
Definition 3.6 (Truth in an RA Model cont.)
For C-, D-, and L-semantics, the clauses for the K operator are:Footnote 21

According to C-semantics, in order for an agent to know φ in world w, all of the ¬φ-possibilities must be eliminated by the agent in w. According to D-semantics, for any φ there is a set \(\text {Min}_{\preceq _{w} }\left(\overline {\left[\left[ \varphi \right]\right] }_{d}\right)\) of most relevant (atw) ¬φ-possibilities that the agent must eliminate in order to know φ. Finally, according to L-semantics, there is a set of relevant possibilities, \(\text {Min}_{\preceq _{w}}\left(W\right)\), such that for any φ, in order to know φ the agent must eliminate the ¬φ-possibilities within that set. Recall the RS ∀∃ vs. RS ∃∀ distinction above.
If φ is true at all pointed models according to X-semantics, then φ is X-valid, written ‘⊨ xφ ’. Since the semantics do not differ with respect to propositional formulas φ, I sometimes omit the subscript in ‘⊨ x ’ and simply write ‘ℳ, w ⊨ φ’. These conventions also apply to the semantics in Definition 4.3.
Since for L-semantics we think of \(\text {Min}_{\preceq _{w}}(W)\) as the set of simply relevant worlds, ignoring the rest of ≤ w , we allow \(\text {Min}_{\preceq _{w}}(W)\) to contain multiple worlds. Hence with L-semantics we assume neither centering nor linearity, which implies centering by Definition 3.1.3b. For D-semantics, whether we assume centering/linearity does not affect our results (as shown in Section 5.2.2).
It is easy to check that according to C/D/L-semantics, whatever is known is true. For D- and L-semantics, Fact 3.7 reflects Lewis’s [52, 554] observation that the veridicality of knowledge follows from his Rule of Actuality, given that an agent can never eliminate her actual world as a possibility. Formally, veridicality follows from the fact that w is minimal in ≤ w and w ⇾ w.
Fact 3.7 (Veridicality)
Kφ → φ is C/D/L-valid.
Consider the model in Fig. 1, drawn for student A in Example 2.1. An arrow from w to v indicates that w ⇾ v, i.e., v is uneliminated by the agent in w. (For all v ∈ W, v ⇾ v, but we omit all reflexive loops). The ordering of the worlds by their relevance at w 1, which we take to be the actual world, is indicated between worlds.Footnote 22 In w 1, the patient has the common condition c, represented by the atomic sentence c true at w 1 (see footnote 7). Possibility w 2, in which the patient has the other common condition c′ instead of c, is just as relevant as w 1. Since the model is for student A, who ran the lab tests to rule out c′, A has eliminated w 2 in w 1. A more remote possibility than w 2 is w 3, in which the patient has the rare disease x. Since A has not run any tests to rule out x, A has not eliminated w 3 in w 1. Finally, the most remote possibility of all is w 4, in which the patient has both c and x. We assume that A has learned from textbooks that x confers immunity to c, so A has eliminated w 4 in w 1.
Now consider C-semantics. In discussing Example 2.1, we held that student A knows that the patient’s condition is c, despite the fact that A did not rule out the remote possibility of the patient’s having x. C-semantics issues the opposite verdict. According to C-semantics, Kc is true at w 1 iff all ¬c-worlds, regardless of their relevance, are ruled out by the agent in w 1. However, w 3 is not ruled out by A in w 1, so Kc is false at w 1. Nonetheless, A has some knowledge in w 1. For example, one can check that K(¬x → c) is true at w 1.
Remark 3.8 (Skepticism)
A skeptic might argue, however, that we have failed to include in our model a particular possibility, far-fetched but uneliminated, in which the patient has neither x nor c, the inclusion of which would make even K(¬x → c) false at w 1 according to C-semantics. In this way, C-semantics plays into the hands of skeptics. By contrast, L- and D-semantics help to avoid skepticism by not requiring the elimination of every far-fetched possibility.
Consider the model in Fig. 1 from the perspective of L-semantics. According to L-semantics, student A does know that the patient has condition c. Kc is true at w 1, because c is true in all of the most relevant and uneliminated (at w 1) worlds, namely w 1 itself. Moreover, although A has not ruled out the possibility w 3 in which the patient has disease x, according to L-semantics she nonetheless knows that the patient does not have x. K¬x is true at w 1, because ¬x is true in all of the most relevant (at w 1) worlds: w 1 and w 2. Indeed, note that K¬x would be true at w 1 no matter how we defined the ⇾ relation is.
Remark 3.9 (Vacuous Knowledge)
What this example shows is that according to L-semantics, in some cases an agent can know some φ with no requirement of ruling out possibilities, i.e., with no requirement on ⇾, simply because none of the accessible ¬φ-possibilities are relevant at w, i.e., because they are not in \(\text {Min}_{\preceq _{w}}(W)\). This is the position of Stine [70, 257] and Rysiew [64, 265], who hold that one can know that skeptical hypotheses do not obtain, without any evidence, simply because the skeptical possibilities are not relevant in the context (also see Lewis [52, 561f]). In general, on the kind of RS ∃∀ view represented by L-semantics, an agent can know a contingent empirical truth φ with no requirement of empirically eliminating any possibilities. Heller [34, 207] rejects such “vacuous knowledge,” and elsewhere I discuss this problem of vacuous knowledge at length ([40]; also see Cohen [13, 99]; Vogel [74, 158f]; and Remark 4.6 below). By contrast, on the kind of RS ∀∃ view represented by D-semantics, as long as there is an accessible ¬φ-possibility, there will be some most relevant (at w) ¬φ-possibility that the agent must rule out in order to know φ in w. Hence D-semantics avoids vacuous knowledge.
D-semantics avoids the skepticism of C-semantics and the vacuous knowledge of L-semantics, but at a cost for closure. Consider the model in Fig. 1 from the perspective of D-semantics. First observe that D-semantics issues our original verdict that student A knows that the patient’s condition is c. Kc is true at w 1 since the most relevant (at w 1) ¬c-world, w 2, is ruled out by A in w 1. K(c ⇾ ¬x) is also true at w 1, since the most relevant (at w 1) ¬(c ⇾ ¬x)-world, w 4, is ruled out by A in w 1. Not only that, but K(c ↔ ¬x) is true at w 1, since the most relevant (at w 1) ¬(c ↔ ¬x)-world, w 2, is ruled out by A in w 1. However, the most relevant (at w 1) x-world, w 3, is not ruled out by A in w 1, so K ¬x is false at w 1. Hence A does not know that the patient does not have disease x. We have just established the second part of the following fact, which matches Dretske’s [19] view. The first part, which follows directly from the truth definition, matches Lewis’s [52, 563n21] view.
Fact 3.10 (Known Implication)
The principles
are C/L-valid, but not D-valid.Footnote 23
In Dretske’s [19, 1007] terminology, Fact 3.10 shows that the knowledge operator in D-semantics is not fully penetrating, since it does not penetrate to all of the logical consequence of what is known. Yet Dretske claims that the knowledge operator is semi-penetrating, since it does penetrate to some logical consequences: “it seems to me fairly obvious that if someone knows that P and Q, he thereby knows that Q” and “If he knows that P is the case, he knows that P or Q is the case” (1009). This is supposed to be the “trivial side” of Dretske’s thesis (ibid.). However, if we understand the RA theory according to D-semantics, then even these monotonicity principles fail (as they famously do for Nozick’s theory, discussed in Section 4, for the same structural reasons).
Fact 3.11 (Distribution and Addition)
The principles
are C/L-valid, but not D-valid.
Proof
The proof of C/L-validity is routine. For D-semantics, the pointed model ℳ, w 1 in Fig. 1 falsifies K(c ∧ ¬x)→ K ¬x and Kc → K(c ∨ ¬x). These principle are of the form Kα → Kβ. In both cases, the most relevant (at w 1) ¬α-world in ℳ is w 2, which is eliminated by the agent in w 1, so Kα is true at w 1. However, in both cases, the most relevant (at w 1) ¬β-world in ℳ is w 3, which is uneliminated by the agent in w 1, so Kβ is false at w 1. □
Fact 3.11 is only the tip of the iceberg, the full extent of which is revealed in Section 5. But it already points to a dilemma. On the one hand, if we understand the RA theory according to D-semantics, then the knowledge operator lacks even the basic closure properties that Dretske wanted from a semi-penetrating operator, contrary to the “trivial side” of his thesis; here we have an example of what I called the problem of containment in Section 1. On the other hand, if we understand the RA theory according to L-semantics, then the knowledge operator is a fully-penetrating operator, contrary to the non-trivial side of Dretske’s thesis; and we have the problem of vacuous knowledge. It is difficult to escape this dilemma while retaining something like Heller’s [33, 34] world-ordering picture with which we started before Definition 3.1. However, Dretske’s [21] discussion of relevancy sets leaves open whether the RA theory should be developed along the lines of this world-ordering picture. In part II, I will propose a different way of developing the theory so that the knowledge operator is semi-penetrating in Dretske’s sense, avoiding the dilemma above.
4 Counterfactuals and Beliefs
In this section, I introduce the formalizations of Heller’s [33, 34] RA theory, Nozick’s [58] tracking theory, and Sosa’s [67] safety theory. Let us begin by defining another class of models, closely related to RA models.
Definition 4.1 (CB Model)
A counterfactual belief model is a tuple ℳ of the form 〈W, D, ≤, V〉 where W , ≤, and V are defined in the same way as W , ≤ , and V in Definition 3.1, and D is a serial binary relation on W .
Notation 3.2 and Definition 3.3 apply to CB models as for RA models, but with ≤ w in place of ≤ w , < w in place of ≺ w , and ≡ w in place of ≃ w .
Think of D as a doxastic accessibility relation, so that w D v indicates that everything the agent believes in w is true in v [51, Section 1.4]. For convenience, we extend the epistemic language of Definition 2.2 to an epistemic-doxastic language with a belief operator B for the D relation. We do so in order to state perspicuous truth definitions for the K operator, which could be equivalently stated in a more direct (though cumbersome) way in terms of the D relation. Our main result will be given for the pure epistemic language.
Think of ≤ w either as a relevance relation as before (for Heller) or as a relation of comparative similarity with respect to world w, used for assessing counterfactuals as in Lewis [49].Footnote 24 With the latter interpretation, we can capture the following well-known counterfactual conditions on an agent’s belief that φ: if φ were false, the agent would not believe φ (sensitivity); if φ were true, the agent would believe φ (adherence); the agent would believe φ only if φ were true (safety). Nozick [58] argued that sensitivity and adherence—the conjunction of which is tracking—are necessary and sufficient for one’s belief to constitute knowledge,Footnote 25 while Sosa [67] argued that safety is necessary. (In Holliday [38, Section 2.D], I consider the revised tracking and safety theories that take into account methods and bases of belief). Following Nozick and Sosa, we can interpret sensitivity as the counterfactual ¬φ □→ ¬Bφ, adherence as φ □→ Bφ, and safety as Bφ □→ φ, with the caveat in Observation 4.5 below. I will understand the truth of counterfactuals following Lewis [49, 20], such that φ □→ ψ is true at a world w iff the closest φ-worlds to w according to ≤ w are ψ-worlds, subject to the same caveat.Footnote 26 The formalization is also compatible with the view that the conditions above should be understood in terms of “close enough” rather than closest worlds.Footnote 27
We are now prepared to define three more semantics for the K operator: H-semantics for Heller, N-semantics for Nozick, and S-semantics for Sosa.
Remark 4.2 (Necessary Conditions)
In defining these semantics, I assume that each theory proposes necessary and sufficient conditions for knowledge. This is true of Nozick’s [58] theory, as it was of Lewis’s [52], but Sosa [67] and Heller [34] propose only necessary conditions. Hence one may choose to read Kφ as “the agent safely believes φ/has ruled out the relevant alternatives to φ” for S/H-semantics. Our results for S/H-semantics can then be viewed as results about the logic of safe belief/the logic of relevant alternatives. However, for reasons similar to those given by Brueckner [10] and Murphy [57], if the subjunctivist or RA conditions are treated as necessary for knowledge, then closure failures for these conditions threaten closure for knowledge itself.Footnote 28 It is up to defenders of these theories to explain why knowledge is closed in ways that their conditions on knowledge are not.
Definition 4.3 (Truth in a CB Model)
Given a well-founded CB model ℳ = 〈W, D, ≤, V〉 with w ∈ W and φ in the epistemic-doxastic language, define ℳ, w ⊨ x φ as follows (with propositional cases as in Def. 3.4):
-
\(\begin {array}{lll} \mathcal {M},w\vDash _{x} B\varphi &\,\mathrm { iff } &\forall v\in W:\mathrm {if }~wD v~\mathrm { then }~ \mathcal {M},v\vDash _{x}\varphi ; \end {array}\)
-
\(\begin {array}{lll} \mathcal {M},w\vDash _{h} K\varphi &\mathrm { iff }& \mathcal {M},w\vDash _{h} B\varphi ~\mathrm { and }\\ &&\mathrm {(sensitivity) } ~\forall v\in \text {Min}_{\leqslant _{w}}\left(\overline {\left[\left[ \varphi \right]\right] }_{h}\right):\mathcal {M},v\nvDash _{h} B\varphi ; \end {array}\)
-
\(\begin {array}{lll} \mathcal {M},w\vDash _{n} K\varphi &\mathrm { iff }&\mathcal {M},w\vDash _{n} B\varphi ~\mathrm { and}\\ &&\mathrm {(sensitivity) } ~\forall v\in ~\text {Min}_{\leqslant _{w}}\left(\overline {\left[\left[ \varphi \right]\right] }_{n}\right):\mathcal {M},v\nvDash _{n} B\varphi ,\\ && \mathrm {(adherence) } ~\forall v\in ~\text {Min}_{\leqslant _{w}}\left(\left[\left[ \varphi \right]\right] _{n}\right):\mathcal {M},v\vDash _{n} B\varphi ; \end {array}\)
-
\(\begin {array}{lll} \mathcal {M},w\vDash _{s} K\varphi &\mathrm { iff }& \mathcal {M},w\vDash _{s} B\varphi ~\mathrm { and} \\ &&\mathrm {(safety) } ~\forall v\in ~\text {Min}_{\leqslant _{w}}\left(\left[\left[ B\varphi \right]\right] _{s}\right):\mathcal {M},v\vDash _{s} \varphi . \end {array}\)
Note that the truth clause for Bφ guarantees doxastic closure (recall Section 2 and see Fact 5.11).Footnote 29
It is easy to check that the belief and subjunctive conditions of H/N/S-semantics together ensure Fact 4.4 (cf. Heller [35, 126]; Kripke [44, 164]).
Fact 4.4 (Veridicality)
Kφ → φ is H/N/S-valid .
Observation 4.5 (Adherence and Safety)
The adherence condition in the N-semantics clause may be equivalently replaced by
the safety condition in the S-semantics clause may be equivalently replaced by
This observation has two important consequences. The first is that in centered models (Def. 3.3.5), adherence (φ □→ Bφ) and safety (Bφ □→ φ) add nothing to belief and true belief, respectively, given standard Lewisian semantics for counterfactuals. DeRose [17, 27n27] takes adherence to be redundant apparently for this reason. But since we only assume weak centering, adherence as above makes a difference—obviously for truth in a model, but also for validity (see Fact 8.8). Nozick [58, 680n8] suggests another way of understanding adherence so that it is non-trivial, but here I will settle on its simple interpretation with weak centering in standard semantics. Whether or not weak centering is right for counterfactuals, adherence and safety can be—and safety typically is—understood directly in terms of what holds in a set of close worlds including the actual world, our \(\text {Min}_{\leqslant _{w}}(W)\) (see note 26), rather than as φ □→ Bφ and Bφ □→ φ.Footnote 30 (Adherence is often ignored). For sensitivity alone, centering vs. weak centering makes no difference for valid principles.
The second consequence is that safety is a ∃∀ condition as in Section 3, where \(\text {Min}_{\leqslant _{w}}(W)\) serves as the set R 𝒞 (w) that is independent of the particular proposition in question (cf. Alspector-Kelly [3, 129n6]). By contrast, sensitivity is obviously a ∀∃ condition, analogous to the D-semantics clause. Viewed this way, in the “subjunctivist-flavored” family of D/H/N/S-semantics, S-semantics is the odd member of the family, since by only looking at the fixed set \(\text {Min}_{\leqslant _{w}}(W)\) in the safety clause, it never uses the rest of the world-ordering.Footnote 31
Figure 2 displays a CB model for Example 2.1. The dotted arrows represent the doxastic relation D. That the only arrow from w 1 goes to itself indicates that in w 1, student A believes that the actual world is w 1, where the patient has c and not x. (We do not require that D be functional, but in Fig. 2 it is.) Hence ℳ, w 1 ⊨ B(c ∧ ¬x). That the only arrow from w 3 goes to w 1 indicates that in w 3, A believes that w 1 is the actual world; since w 3 is the closest (to w 1) x-world, we take this to mean that if the patient’s condition were x, A would still believe it was c and not x (because A did not run any of the tests necessary to detect x).Footnote 32 Hence ℳ, w 1 ⊭ h,n K¬x, because the sensitivity condition is violated. However, one can check that ℳ, w 1 ⊭ h,n K c.
If we were to draw the model for student B, we would replace the arrow from w 2 to w 2 by one from w 2 to w 1, reflecting that if the patient’s condition were c′, B would still believe it was c (because B made the diagnosis of c after only a physical exam, and c and c′ have the same visible symptoms). Hence ℳ′,w 1 ⊭ h, n Kc, where ℳ′ is the model with w 1 Dw 1 instead of w 2 Dw 2.
When we consider S-semantics, we get a different verdict on whether A knows that the patient does not have disease x. Observe that ℳ, w 1 ⊨ s K ¬x, because student A believes ¬x in w 1 and at the closest worlds to w 1, namely w 1 and w 2, ¬x is true. Therefore, A safely believes ¬w in w 1. Similarly ℳ, w 1 ⊨ s Kc, because A safely believes c in w 1. Yet if we add the arrow from w 2 to w 1 for B, one can check that B does not safely believe c at w 1, so ℳ′, w 1 ⊭ s Kc.
Remark 4.6 (Vacuous Knowledge Again)
The fact that ℳ′, w 1 ⊨ s K¬x reflects the idea that the safety theory leads to a neo-Moorean response to skepticism [67], according to which agents can know that skeptical hypotheses do not obtain. In general, a point parallel to that of Remark 3.9 holds for the RS ∃∀ safety theory: if the ¬φ-worlds are not among the close worlds, then one’s belief in φ is automatically safe, no matter how poorly one’s beliefs match the facts in possible worlds (cf. Alspector-Kelly’s [3] distinction between near-safe and far-safe beliefs). This is the version of the problem of vacuous knowledge for the safety theory (see Holliday [40]). By contrast, on the kind of RS ∀∃ theory represented by H/N-semantics, if ¬φ is possible, then knowledge requires that one not falsely believe φ in the closest ¬φ-worlds.
Like D-semantics, H/N-semantics avoid the skepticism of C-semantics and the vacuous knowledge of L/S-semantics, but at a cost for closure. All of the closure principles shown in Facts 3.10 and 3.11 to be falsifiable in RA models under D-semantics are also falsifiable in CB models under H/N-semantics, as one can check at w 1 in Fig. 2. After embracing the “nonclosure” of knowledge under known implication, Nozick [58, 231ff] tried to distinguish successful from unsuccessful cases of knowledge transmission by whether extra subjunctive conditions hold;Footnote 33 but doing so does not eliminate the unsuccessful cases, which go far beyond nonclosure under known implication, as shown in Section 5.
Nozick was well aware that K (φ ∧ ψ) → Kφ ∧ Kψ fails on his theory, and his explanation (beginning “S’s belief that p&q …” on 228) is similar to a proof in our framework. He resisted the idea that Kφ → K (φ ∨ ψ) fails, but he is clearly committed to it.Footnote 34 Vogel’s [76, 76] explanation of why it fails for Nozick is also similar to a proof in our framework, as are Kripke’s [44] many demonstrations of closure failure for Nozick’s theory. Partly in response to these problems, Roush [62, 63] proposes a recursive tracking view of knowledge, in a probabilistic framework, with an additional recursion clause to support closure (see note 26). For discussion of the relation between probabilistic and subjunctivist versions of tracking, see Holliday [38, Section 2.E].
All of the closure principles noted fail for S-semantics as well. For example, it is easy to construct a model in which B (φ ∧ ψ) and hence Bφ are true at a world w, all worlds close to w satisfy B (φ ∧ ψ) → φ ∧ ψ, and yet some worlds close to w do not satisfy Bφ ⇾ Bφ, resulting in a failure of B (φ ∧ ψ) → Kφ at w. Murphy’s [56, 57, Section 4.3] intuitive examples of closure failure for safety have exactly this structure.Footnote 35 We return to this problem for safety in Section 9.
Now it is time to go beyond case-by-case assessment of closure principles. In the following sections, we will turn to results of a more general nature.
5 The Closure Theorem and Its Consequences
In this section, I state the main result of the paper, Theorem 5.2, which characterizes the closure properties of knowledge for the theories we have formalized. Despite the differences between the RA, tracking, and safety theories of knowledge as formalized by D/H/N/S-semantics, Theorem 5.2 provides a unifying perspective: the valid epistemic closure principles are essentially the same for these different theories, except for a twist with the theory of total RA models. For comparison, I also include C/L-semantics, which fully support closure.
Formally, Theorem 5.2 is the same type of result as the “modal decomposition” results of van Benthem [8, Section 4.3, 10.4] for the weakest normal modal logic K and the weakest monotonic modal logic M (see Chellas [12, Section 8.2]). From Theorem 5.2 we obtain decidability (Corollary 5.9) and completeness (Corollary 7.1) results as corollaries. From the proof of the theorem, we obtain results on finite models (Corollary 5.24) and complexity (Corollary 5.25).
The following notation will be convenient throughout this section.
Notation 5.1 (Closure Notation)
Given (possibly empty) sequences of formulas φ 1,…, φ n and ψ 1,…, ψ m in the epistemic language and a propositional conjunction φ 0, we use the notation
Call such a χ n, m a closure principle.Footnote 36
Hence a closure principle states that if the agent knows each of φ 1 through φ n (and the world satisfies a non-epistemic φ 0), then the agent knows at least one of ψ 1 through ψ m . Our question is: which closure principles are valid?
Theorem 5.2 is the answer. Its statement refers to a “T-unpacked” closure principle, a notion not yet introduced. For the first reading of the theorem, think only of flat formulas χ n, m without nesting of the K operator (Def. 2.2), which are T-unpacked if φ 1 ∧ ⋯ ∧ φ n is a conjunct of φ 0. Or we can ignore T-unpacking for flat χ n, m and replace condition (a) of the theorem by
-
(a)′
φ 0 ∧ ⋯ ∧ φ n → ⊥ is valid.
Example 5.8 will show the need for T-unpacking, defined in general in Section 5.2.1.
Theorem 5.2 (Closure Theorem)
Let
be a T-unpacked closure principle.
-
1.
χ n, m is C/L-valid over relevant alternatives models iff
-
(a) φ 0 → ⊥ is valid or
-
(b) for some ψ ∈ {ψ 1,…, ψ m }, φ 1 ∧⋯ ∧φ n → ψ is valid;
-
-
2.
χ n, m is D-valid over total relevant alternatives models iff (a) or
-
(c) for some Φ ⊆ {φ 1,…, φ n, m } and nonempty Ψ ⊆ {ψ 1, …, ψ m }, Footnote 37 \(\underset {\varphi \in \Phi }{\displaystyle \bigwedge }\varphi \leftrightarrow \underset {\psi \in \Psi }{\displaystyle \bigwedge }\psi ~is~valid;\)
-
-
3.
χ n, m is D-valid over all relevant alternatives models iff (a) or
-
(d) for some Φ ⊆ {φ 1,…, φ n } and ψ ∈ {ψ 1,…, ψ m },\(\underset {\varphi \in \Phi }{\displaystyle \bigwedge }\varphi \leftrightarrow \psi ~is~valid.\)
-
-
4.
χ n, m is H/N/S-valid over counterfactual belief models if (a) or (d); Footnote 38 and a flat χ n, m is H/N/S-valid over such models only if (a) or (d).
The remarkable fact established by Theorem 5.2 that D/H/N/S-semantics validate essentially the same closure principles, except for the twist of totality in (c), further supports talk of their representing a “family” of subjunctivist-flavored theories of knowledge. Although results in Section 8.2 (Facts 8.8.4, 8.8.5, and 8.10.1) show that the ‘only if’ direction of part 4 does not hold for some principles involving higher-order knowledge, the agreement between D/H/N/S-semantics on the validity of flat closure principles is striking.
Remark 5.3 (Independence from Assumptions)
Recalling the types of orderings in Definition 3.3, it is noteworthy that parts 1 and 4 of Theorem 5.2 are independent of whether we assume totality (or universality), while parts 2 and 3 are independent of whether we assume centering, linearity (see Section 5.2.2), or universality (see Prop. 5.23). For parts 1–4, we can drop our running assumption of well-foundedness, provided we modify the truth definitions accordingly (see Remark 5.13). Finally, part 1 for L-semantics (but not C-semantics) and parts 2–3 for D-semantics are independent of additional properties of ⇾ such as transitivity and symmetry (see Remark 5.20 and Example 8.1).
To apply the theorem, observe that Kp ∧ K (p → q) → Kq is not D/H/N/S-valid, because p ∧ (p → q) → ⊥ is not valid, so (a)′ fails, and none of
are valid, so there are no Φ and Ψ/ψ as described. Hence (c)/(d) fails.
On the other hand, we now see that Kp ∧ Kq → K(p ∧ q) is D/H/N/S-valid, because p ∧ q ↔ p ∧ q is valid, so we can take Φ = {p, q} and Ψ = {p ∧ q} or ψ = p ∧ q. Besides Kφ → φ (Facts 3.7 and 4.4), this is the first valid principle we have identified for D/H/N/S-semantics, to which we will return in Section 7.
Fact 5.4 (C Axiom)
The principle Kφ ∧ Kψ → K(φ ∧ ψ), known as the C axiom, is D/H/N/S-valid.
To get a feel for Theorem 5.2, it helps to test a variety of closure principles.
Exercise 5.5 (Testing Closure)
Using Theorem 5.2, verify that neither K(p ∧ q) → K(p ∨ q) nor Kp ∧ Kq → K(p ∨ q) are D/H/N/S-valid; verify that K(p ∧ q) → Kp ∨ Kq is only D-valid over total RA models; verify that K(p ∨ q) ∧ K(p → q) → Kq and Kp ∧ K(p → q) →K (p ∧ q) are D/H/N/S-valid.
As if the closure failures of Fact 3.11 were not bad enough, the first three of Exercise 5.5 are also highly counterintuitive. Recall from Section 2 that the Dretske-Nozick case against full closure under known implication, K, had two parts: examples in which K purportedly fails, such as Example 2.1, and theories of knowledge that purportedly explain the failures. For the other principles, we can see why they fail according to the subjunctivist-flavored theories; but without some intuitive examples in which, e.g., arguably an ideally astute logician knows two propositions but not their disjunction, the failure of such weak closure principles according to a theory of knowledge seems to be strong evidence against the theory—even for those sympathetic to the denial of K.
While the closure failures permitted by subjunctivist-flavored theories go too far, in another way they do not go far enough for some purposes. Reflection on the last two principles of Exercise 5.5 suggests they are about as dangerous as K in arguments for radical skepticism about knowledge. The fact that one’s theory validates these principles seems to undermine the force of one’s denying K in response to skepticism, as Nozick [58] uses his subjunctivism to do.
Notwithstanding these negative points against subjunctivist-flavored theories of knowledge, simply replace the K symbol in our language by a neutral □ and Theorem 5.2 can be viewed as a neutral result about the logic of relevant alternatives, of sensitive/truth-tracking belief, and of safe belief (see Section 7).
Parts 3 and 4 of Theorem 5.2 reflect that D-semantics over RA models and H/N/S-semantics over CB models have the following separation property.
Proposition 5.6 (Separation)
For D-semantics (resp. H/N/S-semantics), a closure principle χ n, m (resp. a flat χ n, m ) as in Notation 5.1 with m ≥ 1 is valid iff there is some j ≤ m such that φ 0 ∧Kφ 1 ∧ ⋯ ∧ Kφ n → Kψ j is valid.
The reason for this separation property comes out clearly in the proofs in Sections 5.3 and 5.4. In essence, if the principles with single disjunct consequents are all invalid, then we can glue their falsifying models together to obtain a falsifying model for χ n, m . However, this is not the case for D-semantics over total RA models. The following fact demonstrates the nonequivalence of D-semantics over total RA models and D-semantics over all RA models (as well as H/N/S-semantics over total/all CB models) with an interesting new axiom.
Fact 5.7 (X Axiom)
The principle K(φ ∧ ψ) → Kφ ∨ Kψ, hereafter called the “X axiom” (see Section 7), is D-valid over total RA models, but not D-valid over all RA models or H/N/S-valid over (total) CB models.
Proof
I leave D-validity over total RA models to the reader. Figure 3 displays a non-total RA model that falsifies K(p ∧ q) → Kp ∨ Kq in D-semantics. Since \(\text {Min}_{\preceq _{w}}\left(\overline {\left[\left[ p\wedge q\right]\right] }\right)=\{v,x\}\),  , and
, and  , ℳ , w ⊨
d
K (p ∧ q). Since u and x are incomparable according to ≤
w
, as are y and v, we have \(u\in ~ \text {Min}_{\preceq _{w}}\left(\overline {\left[\left[ p\right]\right] }\right)\) and \(y\in ~ \text {Min}_{\preceq _{w}}\left(\overline {\left[\left[ q\right]\right] }\right)\), which with w ⇾ u and w ⇾ y implies ℳ, w ⊭
d
Kp ∨ Kq. The counterexample for H/N/S-semantics is in Fig. 10, discussed in Section 9. □
, ℳ , w ⊨
d
K (p ∧ q). Since u and x are incomparable according to ≤
w
, as are y and v, we have \(u\in ~ \text {Min}_{\preceq _{w}}\left(\overline {\left[\left[ p\right]\right] }\right)\) and \(y\in ~ \text {Min}_{\preceq _{w}}\left(\overline {\left[\left[ q\right]\right] }\right)\), which with w ⇾ u and w ⇾ y implies ℳ, w ⊭
d
Kp ∨ Kq. The counterexample for H/N/S-semantics is in Fig. 10, discussed in Section 9. □
In Section 7, we will see the role that the X axiom plays in a complete deductive system for D-semantics over total RA models, as well as the role that the C axiom plays in complete deductive systems for D/H/N/S-semantics.
Given the separation property, the proof of the ‘only if’ direction of Theorem 5.2.3 for flat closure principles can be explained roughly as follows.
Proof sketch
Let us try to falsify a flat \(\varphi _{0}\wedge K\varphi _{1}\wedge \dots \wedge K\varphi _{n}\rightarrow K\psi _{j}\). Construct a pointed model ℳ, w with a valuation such that the propositional part φ 0 is true at w.Footnote 39 To make Kψ j false while keeping all Kφ i true at w, we want to add an uneliminated ¬ψ i -world v such that (A) there is no ¬ψ j -world more relevant than v and (B) for any ¬φ i true at v, there is a more relevant ¬φ i -world that is eliminated at w. This is possible if there is a propositional valuation such that ¬ψ j is true at v and for all ¬φ i true at v, \(\psi _{j}\wedge \neg \varphi _{i}\) is satisfiable; for then we can add a satisfying world for each conjunction and make them eliminated and more relevant than v, which gives (A) and (B). If there is no such valuation, then every valuation that satisfies ¬ψ i also satisfies some ¬φ i for which \(\psi _{j}\rightarrow \varphi _{i}\) is valid. Then where Φ is the set of all such \(\varphi _{i}, \neg \psi _{j}\rightarrow \underset {\varphi \in \Phi }{\bigvee }\neg \varphi \) and \(\psi _{j}\rightarrow \underset {\varphi \in \Phi }{\bigwedge }\varphi \) are valid, which means \(\underset {\varphi \in \Phi }{\bigwedge }\varphi \leftrightarrow \psi _{j}\) is valid. □
In Sections 5.2 and 5.3 we give a more precise and general form of the above argument. We conclude this subsection with an example of why Theorem 5.2 requires the notion of T-unpacking, which is defined in general in Definition 5.15.
Example 5.8 (T-unpacking)
As noted before Theorem 5.2, if we consider only flat formulas, then we can ignore T-unpacking, provided we replace condition (a) of Theorem 5.2 by the condition: (a)\('\) \(\varphi _{0}\wedge \dots \wedge \varphi _{n}\rightarrow \bot \) is valid. Let us see why T-unpacking is necessary for non-flat formulas. For example, the formula
is D/H/N/S-valid. Yet none of the following are valid: \(Kp\wedge Kq\rightarrow \bot \), \(Kp\wedge Kq \leftrightarrow p\wedge q\), \(Kp\leftrightarrow p\wedge q\), \(Kq\leftrightarrow p\wedge q\), and \(\top \leftrightarrow p\wedge q\). Hence (5.1) does not satisfy (a)′,(c), or (d) in Theorem 5.2. However, if we T-unpack (5.1) by repeatedly applying the T axiom, \(K\varphi \rightarrow \varphi \), to the antecedent, we obtain
which satisfies (b), (c), and (d) with \(\Phi = \{p,q\}\) and \(\Psi =\{p\wedge q\}\) or \(\psi = p\wedge q\). Hence (5.2) is valid according to Theorem 5.2. Given the validity of the T axiom over RA/CB models (Facts 3.7 and 4.4), (5.1) and (5.2) are equivalent, so (5.1) is valid as well. This example shows the essential idea of T-unpacking, defined formally in Section 5.2.1 and demonstrated again in Example 5.17.
As shown by Proposition 5.16 below, any epistemic formula can be effectively transformed into an equivalent conjunction, each conjunct of which is a T-unpacked formula χ n, m as in Notation 5.1. Using Theorem 5.2, the validity of each conjunct can be reduced to the validity of finitely many formulas of lesser modal depth (Def. 2.2). By repeating this process, we eventually obtain a finite set of propositional formulas, whose validity we can decide by truth tables. Thus, Theorem 5.2 yields the following decidability results.
Corollary 5.9 (Decidability)
The problem of checking whether an arbitrary formula is C/L/D-valid or whether a flat formula is H/N/S-valid over (total or all) RA/CB models is decidable.
In addition, Theorem 5.2 will yield axiomatization results in Corollary 7.1. As Corollary 7.1 will show, the ‘if’ direction of each ‘iff’ statement in Theorem 5.2 is a soundness result, while the ‘only if’ direction is a completeness result. We prove soundness in Section 5.1 and completeness in Sections 5.2–5.4.
5.1 Soundness
In the ‘if’ direction, part 1 of Theorem 5.2 is a simple application of the C/L-truth definitions, which we skip. For parts 2–4, we use the following lemma.
Lemma 5.10 (Min Inclusion)
-
1.
If condition (c) of Theorem 5.2 holds, then for any well-founded and total pointed RA/CB model ℳ, w,Footnote 40 there is some ψ ∈ Ψ such that \(\text {Min}_{\leq _{w}}\left(\overline {\left[\left[ \psi \right]\right] }\right)\subseteq \underset {\varphi \in \Phi }{\displaystyle \bigcup }~\text {Min}_{\leq _{w}}\left(\overline {\left[\left[ \varphi \right]\right] }\right).\)
-
2.
If condition (d) of Theorem 5.2 holds, then for any well-founded pointed RA/CB model ℳ, w,\(\text {Min}_{\leq _{w}}\left(\overline {\left[\left[ \psi \right]\right] }\right)\subseteq \underset {\varphi \in \Phi }{\displaystyle \bigcup }~\text {Min}_{\leq _{w}}\left(\overline {\left[\left[ \varphi \right]\right] }\right).\)
Proof
For part 1, assume for reductio that (c) holds and there is some well-founded and total ℳ, w such that for all ψ ∈ Ψ there is some \(u_{\psi }\) with
and
Given (c), (5.3) implies \(u_{\psi }\in \overline {\left[\left[ \varphi _{\psi }\right]\right] }\) for some \(\varphi _{\psi }\in \Phi \). Since ≤ w is well-founded, there is some
Given (c), (5.5) implies \(v\in \overline {\left[\left[ \psi \right]\right] }\) for some ψ ∈ Ψ. Hence \(u_{\psi }\leq _{w} v\) by (5.3) and the totality of ≤ w . Together \(u_{\psi }\leq _{w} v\), \(u_{\psi }\in \overline {\left[\left[ \varphi _{\psi }\right]\right] }\), (5.5), and the transitivity of ≤ w imply
which contradicts (5.4) by basic set theory.
For part 2, assume for reductio that (d) holds and there is some well-founded ℳ, w and \(u_{\psi }\) such that (5.3) and 5.4 hold for ψ. Given (d), (5.3) implies \(u_{\psi }\in \overline {\left[\left[ \varphi _{\psi }\right]\right] }\) for some \(\varphi _{\psi }\in \Phi \). Hence by the well-foundedness of ≤ w and (5.4) there is some \(v\in \overline {\left[\left[ \varphi _{\psi }\right]\right] }\) such that \(v<_{w} u_{\psi } \). Given (d), \(v\in \overline {\left[\left[ \varphi _{\psi }\right]\right] }\) implies \(v\in \overline {\left[\left[ \psi \right]\right] }\), which with \(v<_{w} u_{\psi } \) contradicts (5.3). □
For the H/N/S-semantics cases, we will also use a basic fact of normal modal logic (see Theorem 3.3(2) of Chellas [12]), namely that the truth clause for B in Definition 4.3 guarantees Fact 5.11 below. Note that we do not require full doxastic closure, but only as much doxastic closure as needed to support the limited forms of epistemic closure that are valid for H/N/S-semantics.
Fact 5.11 (Partial Doxastic Closure)
For x ∈ {h, n, s}, if \(\vDash _{x} \underset {\varphi \in \Phi }{\bigwedge }\varphi \leftrightarrow \psi \), then \(\vDash _{x} \underset {\varphi \in \Phi }{\bigwedge } B\varphi \leftrightarrow B\psi \).
For convenience, we will use the following notation throughout this section.
Notation 5.12 (Relational Image)
Given ℳ = 〈W, ⇾, ≤, W〉, the image of {w} under the relation ⇾ by ⇾ (w) = {v ∈ W ∣ w ⇾ v}.
Hence ⇾(w) is the set of uneliminated possibilities for the agent in w.
We are now ready to prove the ‘if’ directions of Theorem 5.2.2–4.
Claim
If (a) or (c) holds, then χ n, m is D-valid over total RA models; if (a) or (d) holds, then it is D-valid over RA models and H/N/S-valid over CB models.
Proof
If (a) holds, then it is immediate that χ n, m is D/H/N/S-valid, since its antecedent is always false. For (c) and (d), we consider each of the D/H/N/S-semantics in turn, assuming for an arbitrary pointed RA/CB model ℳ, w that
To show ℳ, w ⊨ x χ n,m , it suffices to show ℳ, w ⊨ x Kψ j for some j ≤ m.
If (5.7) holds for x := d, then by the truth definition (Def. 3.6),

If ℳ is a total (resp. any) RA model, then by (c) and Lemma 5.10.1 (resp. by (d) and Lemma 5.10.2), (5.8) implies that there is some ψ ∈ Ψ (resp. that the ψ in (d) is) such that  whence \(\mathcal {M},w \vDash _{d} K\psi \).
whence \(\mathcal {M},w \vDash _{d} K\psi \).
For the cases of H/N/S-semantics, it follows from (d) and Fact 5.11 that
If (5.7) holds for x := h, then by the truth definition (Def. 4.3),
By (5.9), the first conjunct of (5.10) implies \(\mathcal {M},w \vDash _{h} B\psi \). By (d), Lemma 5.10.2, and (5.9), the second conjunct implies the sensitivity condition that \(\text {Min}_{\leqslant _{w}}\left(\overline {\left[\left[ \psi \right]\right] }\right)\subseteq \overline {\left[\left[ B\psi \right]\right] }\). Hence \(\mathcal {M},w \vDash _{h} K\psi \).
If (5.7) holds for x := n, then by the truth definition (Def. 4.3), (5.10) holds with n in place of h. So by the same argument as before, sensitivity holds for ψ at w, which with \(\mathcal {M},w\vDash _{n} B\psi \) and \(w\in ~\text {Min}_{\leqslant _{w}}(W)\) (Def. 3.1.3b) implies \(\mathcal {M},w\vDash _{n}\psi \). It follows that \(\text {Min}_{\leqslant _{w}}(\left[\left[ \psi \right]\right] )\subseteq ~ \text {Min}_{\leqslant _{w}}(W)\), which with (d) implies
Since the adherence condition must hold for each \(\varphi \in \Phi \) at w,
which with (5.11) and (5.9) implies \(\text {Min}_{\leqslant _{w}}(\left[\left[ \psi \right]\right] )\subseteq \left[\left[ B\psi \right]\right] \). Thus, adherence and sensitivity hold for ψ at w, so \(\mathcal {M},w \vDash _{n} K\psi \) given \(\mathcal {M},w \vDash _{n} B\psi \).
If (5.7) holds for x := n, then by the truth definition (Def. 4.3),
By (5.9), the first conjunct of (5.13) implies \(\mathcal {M},w \vDash _{s} B\psi \). Given \(w\in ~ \text {Min}_{\leqslant _{w}}(W)\) (Def. 3.1.3b), it follows that \(\text {Min}_{\leqslant _{w}}(\left[\left[ B\psi \right]\right] ) \subseteq ~\text {Min}_{\leqslant _{w}}(W)\) and therefore
by (5.9). Finally, from (d) we have
which with (5.14) and the second conjunct of (5.13) implies the safety condition that \( \text {Min}_{\leqslant _{w}}(\left[\left[ B\psi \right]\right] ) \subseteq \left[\left[ \psi \right]\right] \), so \(\mathcal {M},w \vDash _{s} K\psi \) given \(\mathcal {M},w \vDash _{s} B\psi \). □
Remark 5.13 (Dropping Well-Foundedness)
We can drop the assumption of well-foundedness used in the above proofs, provided we modify the truth definitions accordingly. For example (cf. Lewis [49, Section 2.3]), we may define

which is equivalent to the clause in Definition 3.6 over (total) well-founded models.Footnote 41 I will give the proof for Theorem 5.2.2 that (c) implies the validity of χ n, m over total RA models according to (5.16). Assume that (5.7) holds for x := d′. If \(\left[\left[ \varphi \right]\right] =W_{w}\) for all \(\varphi \in \Phi \), then by (c), \(\left[\left[ \psi \right]\right] =W_{w}\) and hence \(\mathcal {M},w\vDash _{d'} K\psi \) for all ψ ∈ Ψ. Otherwise, for every \(\varphi \in \Phi \) for which the second case of (5.16) holds, let \(v_{\varphi }\) be a witness to the existential quantifier. Since \(\{v_{\varphi }\mid \varphi \in \Phi \}\) is finite and nonempty, \(\text {Min}_{\preceq _{w}}(\{v_{\varphi }\mid \varphi \in \Phi \})\) is nonempty. Consider some \(v\in \text {Min}_{\preceq _{w}}(\{v_{\varphi }\mid \varphi \in \Phi \})\). Given that ≤ w is a total preorder,

Since \(v\in \overline {\left[\left[ \varphi \right]\right] }\) for some \(\varphi \in \Phi \), by (c) it follows that \(v\in \overline {\left[\left[ \psi \right]\right] }\) for some ψ ∈ Ψ. Now observe that for all \(u\in \overline {\left[\left[ \psi \right]\right] }\), \(u\preceq _{w} v\) implies  . For if \(u\in \overline {\left[\left[ \psi \right]\right] }\), then by (c), \(u\in \overline {\left[\left[ \varphi \right]\right] }\) for some \(\varphi \in \Phi \), in which case \(u\preceq _{w} v\) implies
. For if \(u\in \overline {\left[\left[ \psi \right]\right] }\), then by (c), \(u\in \overline {\left[\left[ \varphi \right]\right] }\) for some \(\varphi \in \Phi \), in which case \(u\preceq _{w} v\) implies  by (5.17). Hence v is a witness to the existential in (5.16) for \(K\psi \), whence \(\mathcal {M},w\vDash _{d'} K\psi \).We leave the other cases without well-foundedness to the reader.Footnote 42
by (5.17). Hence v is a witness to the existential in (5.16) for \(K\psi \), whence \(\mathcal {M},w\vDash _{d'} K\psi \).We leave the other cases without well-foundedness to the reader.Footnote 42
5.2 Completeness for Total RA Models
We turn now to the ‘only if’ directions of Theorem 5.2. The proof for part 1 of the theorem, which we omit, is a much simpler application of the general approach used for the other parts. In this section, we treat the ‘only if’ direction of part 2. This is the most involved part of the proof and takes us most of the way toward the ‘only if’ direction of part 3, treated in Section 5.3. It may help at times to recall the proof sketch given after Fact 5.7 above.
In Section 5.2.1, I define what it is for the χ n, m in Theorem 5.2 to be T-unpacked. In Section 5.2.2, I show that if a T-unpacked χ n, m does not satisfy (a) or (c) of Theorem 5.2, then it is falsified by a finite total RA model according to D-semantics. In fact, it is falsified by a finite linear RA model with the universal field property (Def. 3.3.4). Finally, in Section 5.2.3 we give upper bounds on the size of and complexity of finding falsifying models in Corollaries 5.24 and 5.25.
5.2.1 T-unpacking Formulas
Toward defining what it is for χ n, m (Notation 5.1) to be T-unpacked, let us first define a normal form for the \(\varphi _{1},\dots ,\varphi _{n}\) in χ n, m . For our purposes, we need only define the normal form for the top (propositional) level of each φ i .
Definition 5.14 (DNF)
A formula in the epistemic language is in (propositional) disjunctive normal form (DNF) iff it is of the form
where α is propositional (a conjunction of literals, but it will not matter here), and \(\beta \) and \(\gamma \) are any formulas.
Roughly speaking, we T-unpack a conditional χ n, m by using the T axiom, \(K\varphi _{i}\rightarrow \varphi _{i}\), to replace \(K\varphi _{i}\) in the antecedent with the equivalent \(\varphi _{i}\wedge K\varphi _{i}\) and then use propositional logic to put \(\varphi _{i}\) in its appropriate place; e.g., if \(\varphi _{i}\) is \(\neg K\gamma \), then we move \(K\gamma \) to the consequent to become one of the \(K\psi \)’s. After the following general definition and result, we work out a concrete example.
Definition 5.15 (T-unpacked)
For any (possibly empty) sequence of formulas \(\psi _{1},\dots ,\psi _{m}\), a formula of the form \(\chi _{0,m}\) is T-unpacked; and for \(\varphi _{n+1}\) in DNF, a formula of the form \(\chi _{n+1,m}\) is T-unpacked iff χ n, m is T-unpacked and there is a disjunct δ of \(\varphi _{n+1}\) such that:
-
1.
the α conjunct in δ is a conjunct of \(\varphi _{0}\);
-
2.
for all Kβ conjuncts in δ, there is some \(i\leq n\) such that \(\varphi _{i} = \beta \);
-
3.
for all \(\neg K\gamma \) conjuncts in δ, there is some \(j\leq m\) such that \(\psi _{j} = \gamma \).
The following proposition will be used to prove several later results.
Proposition 5.16 (T-unpacking)
Every formula in the epistemic language is equivalent over RA models in C/D/L-semantics (and over CB models in H/N/S-semantics) to a conjunction of T-unpacked formulas of the form χ n, m .
Proof
By propositional logic, every formula θ is equivalent to a conjunction of formulas of the conditional (disjunctive) form χ n, m . Also by propositional logic, every \(\varphi _{i}\) in the antecedent of χ n, m can be converted into an equivalent \(\varphi _{i}^{\vee }\) in DNF; and since \(\varphi _{i}\) and \(\varphi _{i}^{\vee }\) are equivalent, so are \(K\varphi _{i}\) and \(K\varphi _{i}^{\vee }\) by the semantics. To obtain an equivalent of θ in which each χ n, m is T-unpacked, we repeatedly use the following equivalences, easily derived using propositional logic and the valid T axiom, Kψ ⇾ ψ. Where ζ and η are any formulas,
where each \(\delta _{k}\) is of the form \(\alpha ^{k}\wedge \bigwedge K\beta ^{k} \wedge \bigwedge \neg K\gamma ^{k}\). Compare conditions 1–3 of Definition 5.15 to the relation of \(\delta _{k}\) to the k-th conjunct in the last line. □
Example 5.17 (T-unpacking cont.)
Let us T-unpack the following formula:
No matter what we substitute for ψ, the form of the final result will be the same, since T-unpacking does nothing to formulas already in the consequent.
As in the proof of Proposition 5.16, we derive a string of equivalences, obtaining formulas in boldface by applications of the T axiom and otherwise using only propositional logic:
then since φ is a disjunction, we split into two conjuncts:
then we move the negated \(K\gamma _{1}^{1}\) in δ 1 to the first consequent and rewrite as
then we apply the T axiom to the Kβ formulas:
then we move the negated Kq in \(\beta _{2}^{1}\) and Kr in \(\beta _{1}^{2}\) to the consequents:
since \(\beta _{1}^{1}\) is another disjunction, we split the first conjunct into two:
finally, we apply the T axiom to Kp and rewrite as:
.
Observe that the three conjuncts are T-unpacked according to Definition 5.15.
5.2.2 Countermodel Construction
Our approach to proving the ‘only if’ direction of Theorem 5.2.2 is to assume that (a) and (c) fail, from which we infer the existence of models that can be “glued together” to construct a countermodel for χ n, m . For a clear illustration of this approach applied to basic modal models with arbitrary accessibility relations, see van Benthem [8, Section 4.3]. There are two important differences in what we must do here. First, since we are dealing with reflexive models in which \(K\varphi \rightarrow \varphi \) is valid, we must use T-unpacking. Second, since we are dealing with a hybrid of relational and ordering semantics, we cannot simply glue all of the relevant models together at once, as in the basic modal case; instead, we must put them in the right order, which we do inductively.
The construction has two main parts. First, we inductively build up a kind of “pre-model” that falsifies χ n, m . Second, assuming that χ n, m is T-unpacked, we can then convert the pre-model into an RA model that falsifies χ n, m .
Definition 5.18 (Pre-model)
A pointed pre-model is a pair ℳ, v, with ℳ = 〈W, ⇾, ≤, V〉 and v ∈ W, where W , ⇾, ≤ w for w ∈ W ∖ {v}, and V are as in Definition 3.1; ≤ v satisfies Definition 3.1.3a, but for all w ∈ W, v ∉ W w .
Hence a pointed pre-model is not a pointed RA model, since Definition 3.1.3b requires that v ∈ W v for an RA model. However, truth at a pointed pre-model is defined in the same way as truth at a pointed RA model in Definition 3.6.
The following lemma shows how we will build up our model in the inductive construction of Lemma 5.21. It is important to note that Lemmas 5.19 and 5.21 hold for any χ n, m as in Notation 5.1, whether or not it is T-unpacked.
Lemma 5.19 (Pre-model Extension)
Assume there is a linear pointed pre-model ℳ, w such that ℳ, w ⊭ d χ n,m .
-
1.
If ψ 1 ∧ ⋯ ∧ → φ n+1 is not D-valid over linear RA models, then there is a linear pointed pre-model ℳ ♯, w such that ℳ ♯, ⊭ d χ n+1,m .
-
2.
If ψ 1 ∧ ⋯ ∧ → ψ m+1 is not D-valid over linear RA models, then there is a linear pointed pre-model ℳ ♭, w such that ℳ ♭, ⊭ d χ n,m+1.
Proof
For part 1, let 𝒩 = 〈N, →𝒩, ≤𝒩, V 𝒩〉 with v ∈ N be a linear RA model such that 𝒩, v ⊭ d ψ 1 ∧⋯ ∧ ψ m → φ n+1. By assumption, there is a linear pre-model ℳ = 〈N, ⇾ℳ, ≤ℳ, V ℳ〉 with point w ∈ M such that ℳ, w ⊭ d χ n,m . Define ℳ ♯ = 〈W ♯, ⇾♯, ≤♯, V ♯〉 as follows (see Fig. 4):

Observe that ℳ ♯, w is a linear pointed pre-model.
It is easy to verify that for all formulas ξ and x ∈ M ∖ {w},
Given \(\mathcal {M},w\nvDash _{d} \chi _{n,m}\) and the truth definition (Def. 3.6),

It follows by the construction of \(\mathcal {M}^{\sharp }\) and (5.18) that

which is equivalent to \(\mathcal {M}^{\sharp },w\vDash _{d} K\varphi _{1}\wedge \dots \wedge K\varphi _{n+1}\) by the truth definition. The construction of \(\mathcal {M}^{\sharp }\) and (5.18) also guarantee that for all \(k\leq m\),

Given \(\mathcal {M},w\nvDash _{d} \chi _{n,m}\), for all \(k\leq m\) the left side of (5.21) is nonempty, so the right side is nonempty. Hence by the truth definition, \(\mathcal {M}^{\sharp },w\nvDash _{d} K\psi _{1}\vee \dots \vee K\varphi _{m}\). Finally, since \(\varphi _{0}\) is propositional, \(\mathcal {M},w\vDash \varphi _{0}\) implies \(\mathcal {M}^{\sharp },w\vDash \varphi _{0}\) by definition of \(V^{\sharp }\). It follows from the preceding facts that \(\mathcal {M}^{\sharp },w\nvDash _{d} \chi _{n+1,m}\).
For part 2, let 𝒪 = 〈O, ⇾𝒪, ≤𝒪, V 𝒪〉 with \(u\in O\) be a linear RA model such that \(\mathcal {O},u\nvDash _{d} \varphi _{1}\wedge \dots \wedge \varphi _{n} \rightarrow \psi _{m+1}\). Given ℳ, w as in part 1, define ℳ ♭ = 〈W ♭, ⇾♭, ≤♭, V ♭〉 from ℳ and 𝒪 in the same way as we defined \(\mathcal {M}^{\sharp }\) from ℳ and 𝒩 for part 1, except that ⇾♭ = ⇾ℳ ∪ ⇾ 𝒪 ∪ {w, u} (see Fig. 5). Observe that ℳ ♭,w is a linear pointed pre-model.
It is easy to verify that for all formulas ξ and \(x\in M\setminus \{w\}\),
As in the proof of part 1, (5.19) holds for ℳ. It follows by the construction of ℳ
♭
ℳ
♭ and (5.22) that (5.19) also holds for ℳ
♭ and ⇾♭ in place of ℳ and⇾ℳ, so ℳ
♭, w ⊨
d
K
d1 ∧ ⋯ ∧ K
φn
by the truth definition. Also as in the proof of part 1,  is nonempty for all K ≤ m. It follows by the construction of ℳ
♭ and (5.22) that
is nonempty for all K ≤ m. It follows by the construction of ℳ
♭ and (5.22) that  is nonempty for all k ≤ m + 1, so ℳ
♭, w ⊭ ψ
1 ∨ ⋯ ∨ Kψ
m+1 by the truth definition. Finally, since φ
0 is propositional, ℳ, w ⊨ φ
0 implies ℳ
♭, w ⊨ φ
0 by definition of V
♭. It follows from the preceding facts that ℳ
♭, u ⊭
d
χ
n,m+1. □
is nonempty for all k ≤ m + 1, so ℳ
♭, w ⊭ ψ
1 ∨ ⋯ ∨ Kψ
m+1 by the truth definition. Finally, since φ
0 is propositional, ℳ, w ⊨ φ
0 implies ℳ
♭, w ⊨ φ
0 by definition of V
♭. It follows from the preceding facts that ℳ
♭, u ⊭
d
χ
n,m+1. □
Remark 5.20 (Properties of ⇾)
Lemma 5.19 also holds for the class of RA models/pre-models in which ⇾ is an equivalence relation, so that Theorem 5.2.2–3 will as well. For part 1, if ℳ and 𝒩 are in this class, so is ℳ ♯, since the union of two disjoint equivalence relations is an equivalence relation. For part 2, suppose ℳ and 𝒪 are in the class. Since we have added an arrow from w to u, ℳ ♭ may not be in the class. In this case, let ⇾+ be the minimal extension of ⇾♭ that is an equivalence relation. One can check that by construction of ℳ ♭, for all w ∈ W ♭,
(⇾+(w)∖ ⇾♭ (w)) ∩ W w = ∅.
It follows that ℳ ♭ and ℳ + = 〈W ♭, ⇾+, ≤♭, V ♭ satisfy the same formulas according to D-semantics.
Using Lemma 5.19, we can now carry out our inductive construction.
Lemma 5.21 (Pre-model Construction)
If neither (a) nor (c) of Theorem 5.2 holds for χ n, m , then there is a linear pointed pre-model ℳ, w such that \(\mathcal {M},w\nvDash _{d} \chi _{n,m}\).
Proof
The proof is by induction on m with a subsidiary induction on n.
Base Case for m Assume that neither (a) nor (c) holds for \(\chi _{n,0}\).Footnote 43 Let ℳ = 〈W, ⇾, ≤, V〉 be such that W = {w}, ⇾ = {〈w, w〉}, ≤ W = ∅, and V is any valuation such that \(\mathcal {M},w\vDash \varphi _{0}\), which exists since (a) does not hold for \(\chi _{n,0}\). Then ℳ, w is a linear pointed pre-model such that \(\mathcal {M},w\nvDash _{d} \chi _{n,0}\).
Inductive Step for m Assume for induction on m that for any \(\beta _{1},\dots ,\beta _{m}\) and any n, if neither (a) nor (c) holds for \(\chi :=\varphi _{0} \wedge K\varphi _{1}\wedge \dots \wedge K\varphi _{n}\rightarrow K\beta _{1}\vee \dots \vee K\beta _{m}\), then there is a linear pointed pre-model ℳ, w with \(\mathcal {M},w\nvDash _{d} \chi \). Assume that for some \(\psi _{1},\dots ,\psi _{m+1}\), neither (a) nor (c) holds for \(\chi _{n,m+1}\). We prove by induction on n that there a linear \(\mathcal {M}',w\) with \(\mathcal {M}',w\nvDash _{d} \chi _{n,m+1}\).
Base Case for n Assume neither (a) nor (c) holds for \(\chi _{0,m+1}\). Since (c) does not hold, for all \(j\leq m+1\), \(\nvDash _{d} \top \leftrightarrow \psi _{j}\) and hence \(\nvDash _{d} \top \rightarrow \psi _{j}\). Starting with ℳ, w defined as in the base case for m such that \(\mathcal {M},w\nvDash \chi _{0,0}\), apply Lemma 5.19.2 \(m+1\) times to obtain an \(\mathcal {M}',w\) with \(\mathcal {M}',w\nvDash \chi _{0,m+1}\).
Inductive Step for n Assume for induction on n that for any \(\alpha _{0},\dots ,\alpha _{n}\), if neither (a) nor (c) holds for \(\chi :=\alpha _{0} \wedge K\alpha _{1}\wedge \dots \wedge K\alpha _{n}\rightarrow K\psi _{1}\vee \dots \vee K\psi _{m+1}\), then there is a linear pointed pre-model ℳ, w with \(\mathcal {M},w\nvDash _{d} \chi \). Assume that for some \(\varphi _{0},\dots ,\varphi _{n+1}\), neither (a) nor (c) holds for \(\chi _{n+1,m+1}\).
Case 1 \(\vDash _{d} \varphi _{1}\wedge \dots \wedge \varphi _{n+1}\rightarrow \psi _{1}\wedge \dots \wedge \psi _{m+1}\). Then since (c) does not hold for \(\chi _{n+1,m+1}\), \(\nvDash _{d} \psi _{1}\wedge \dots \wedge \psi _{m+1} \rightarrow \varphi _{1}\wedge \dots \wedge \varphi _{n+1}\), in which case \(\nvDash _{d} \psi _{1}\wedge \dots \wedge \psi _{m+1} \rightarrow \varphi _{i}\) for some \(i \leq n+1\). Without loss of generality, assume
Since neither (a) nor (c) holds for \(\chi _{n+1,m+1}\), neither holds for \(\chi _{n,m+1}\). Hence by the inductive hypothesis for n there is a linear pointed pre-model ℳ, w such that \(\mathcal {M},w\nvDash _{d} \chi _{n,m+1}\), which with (5.23) and Lemma 5.19.1 implies that there is a linear pointed pre-model \(\mathcal {M}^{\sharp },w\) such that \(\mathcal {M}^{\sharp },w\nvDash _{d} \chi _{n+1,m+1}\).
Case 2 \(\nvDash _{d} \varphi _{1}\wedge \dots \wedge \varphi _{n+1}\rightarrow \psi _{1}\wedge \dots \wedge \psi _{m+1}\). Then for some \(j \leq m+1\), \(\nvDash \varphi _{1}\wedge \dots \wedge \varphi _{n+1}\rightarrow \psi _{j}\). Without loss of generality, assume
Since neither (a) nor (c) holds for \(\chi _{n+1,m+1}\), neither holds for \(\chi _{n+1,m}\). Hence by the inductive hypothesis for m there is a linear pointed pre-model ℳ, w such that ℳ, w ⊭ d χ n+1,m , which with (5.24) and Lemma 5.19.2 implies that there is a linear pointed pre-model ℳ ♭, w such that ℳ ♭, w ⊭ d χ n+1,m+1. □
Finally, if χ n, m is T-unpacked (Def. 5.15), then we can convert the falsifying pre-model obtained from Lemma 5.21 into a falsifying RA model.
Lemma 5.22 (Pre-model to Model Conversion)
Given a linear pointed pre-model ℳ, w and a T-unpacked χ n, m such that \(\mathcal {M},w\nvDash _{d}\chi _{n,m}\), there is a linear pointed RA model \(\mathcal {M}^{c},w\) such that \(\mathcal {M}^{c},w\nvDash _{d}\chi _{n,m}\).
Proof
Where ℳ =〈W, ⇾, ≤, V〉, define ℳ c = 〈W, ⇾, ≤c, V〉 such that for all v ∈ W∖{w}, \(\preceq _{v}^{c}\,=\,\preceq _{v}\), and \(\preceq _{w}^{c}\,=\,\preceq _{w}\cup \,\{\langle w,v \rangle \mid v\in \{w\}\cup W_{w} \}\), where \(W_{w}\) is the field of ≤ w . Since w is strictly minimal in \(\preceq _{w}^{c}\), \(\mathcal {M}^{c}\) is a linear RA model. (Note, however, that w is still not in the field of \(\preceq _{v}^{c}\) for any \(v\in W\setminus \{w\}\).) By construction of \(\mathcal {M}^{c}\), together \(\mathcal {M},w\nvDash _{d} K\psi _{1}\vee \dots \vee K\psi _{m}\) and w ⇾ w imply
We prove by induction that for all \(k\leq n\),
The base case of \(k=0\) is immediate since \(\varphi _{0}\) is propositional, \(\mathcal {M},w\vDash \varphi _{0}\), and ℳ and \(\mathcal {M}^{c}\) have the same valuations. Assuming (5.26) holds for \(k<n\), we must show \(\mathcal {M}^{c},w\vDash _{d} K\varphi _{k+1}\). Since χ
n, m
is T-unpacked, together Definition 5.15, (5.25), and (5.26) imply \(\mathcal {M}^{c},w\vDash _{d} \varphi _{k+1}\). Since \(\mathcal {M},w\vDash _{d} K\varphi _{k+1}\), we have by the truth definition (Def. 3.6). It follows, given the construction of ℳ
c and the fact that ℳ
c, w ⊨
d
φ
k=1 that
by the truth definition (Def. 3.6). It follows, given the construction of ℳ
c and the fact that ℳ
c, w ⊨
d
φ
k=1 that , which gives \(\mathcal {M}^{c},w\vDash _{d} K\varphi _{k+1}\), as desired. □
, which gives \(\mathcal {M}^{c},w\vDash _{d} K\varphi _{k+1}\), as desired. □
The proof of the ‘only if’ direction of Theorem 5.2.2 is complete. By Lemmas 5.21 and 5.22, if a T-unpacked χ n, m does not satisfy (a) or (c) of Theorem 5.2, then it is falsified by a linear—and hence total—RA model according to D-semantics. Indeed, as the next proposition and Corollary 5.24 together show, it is falsified by an RA model with the universal field property (Def. 3.3.4).
Proposition 5.23 (Universalization)
Where ℳ = 〈W, ⇾, ≤, V〉 is a finite RA model, there is a finite RA model ℳ u = 〈W u, ⇾u, ≤u, V u〉 with the universal field property, such that \(W\subseteq W^{u}\) and for all w ∈ W and all φ,
If ℳ is total, \(\mathcal {M}^{u}\) is also total. If ℳ is linear, \(\mathcal {M}^{u}\) is also linear.
Proof
Given ℳ = 〈W, ⇾, ≤, V, suppose that for some w, v ∈ W, v ∉ W w , so v ≠ w. Define ℳ′ = 〈W′, ⇾′, ≤′ V′〉 such that W′ = W; ⇾′ = ⇾ ∖{〈w, v〉}; \(\preceq _{w}' \,=\, \preceq _{w} \cup \,\{\langle x,v\rangle \mid x\in W_{w}\cup \{v\} \}\); \(\preceq _{y}' \,=\,\preceq _{y}\) for \(y\in W\setminus \{w\}\); and \(V' =V\). In other words, v becomes the least relevant world at w and eliminated at w in \(\mathcal {M}'\). Given \(v\not \in W_{w}\), one can show by induction on φ that for all \(x\in W\), \(\mathcal {M},x\vDash _{d} \varphi \) iff \(\mathcal {M}',x\vDash _{d} \varphi \). Applying the transformation \(\mathcal {M}\mapsto \mathcal {M}'\) successively no more than \(|W|^{2}\) times with other pairs of worlds like w and v yields a model \(\mathcal {M}^{u}\) with the universal field property. If ℳ is total/linear, so is \(\mathcal {M}^{u}\).
If we require that ⇾ be an equivalence relation, then the transformation above will not work in general, since we may lose transitivity or symmetry by setting  . To solve this problem, we first make an isomorphic copy of ℳ, labeled ℳ
⋆ = 〈W
⋆, ⇾⋆, ≤⋆, V
⋆〉. For every w ∈ W, let w
⋆ be its isomorphic copy in W
⋆. Define 𝒩 = 〈W
𝒩, ⇾𝒩, ≤𝒩, V
𝒩 as follows: W
𝒩 = W ∪ W
⋆; ⇾𝒩 = ⇾ ∪ ⇾⋆; V
𝒩 (p) = V(p) ∪ V
⋆ (p); for all w ∈ W, \(\preceq _{w}^{\mathcal {N}}\,=\,\preceq _{w}\cup \,\{\langle v,u\rangle \mid v\in W^{\mathcal {N}}~\mathrm { and }~u\in W^{\star }\}\); for all \(w^{\star }\in W^{\star }\), \(\preceq _{w^{\star }}^{\mathcal {N}}\,=\,\preceq _{w^{\star }}\cup \, \{\langle v,u\rangle \mid v\in W^{\mathcal {N}}~\mathrm { and }~u\in W\}\). In other words, 𝒩 is the result of first taking the disjoint union of ℳ and ℳ
⋆ (so there are no v ∈ W and u ∈ W
⋆ such that v ⇾𝒩
u or u ⇾𝒩
v) and then making all worlds in \(W^{\star }\) the least relevant worlds from the perspective of all worlds in W , and vice versa.Footnote 44 Given this construction, it is easy to prove by induction that for all w ∈ W and formulas φ, \(\mathcal {M},w\vDash _{d}\varphi \) iff \(\mathcal {N},w\vDash _{d}\varphi \) iff \(\mathcal {N},w^{\star }\vDash _{d}\varphi \). Moreover, ⇾𝒩 is an equivalence relation if ⇾ is.
. To solve this problem, we first make an isomorphic copy of ℳ, labeled ℳ
⋆ = 〈W
⋆, ⇾⋆, ≤⋆, V
⋆〉. For every w ∈ W, let w
⋆ be its isomorphic copy in W
⋆. Define 𝒩 = 〈W
𝒩, ⇾𝒩, ≤𝒩, V
𝒩 as follows: W
𝒩 = W ∪ W
⋆; ⇾𝒩 = ⇾ ∪ ⇾⋆; V
𝒩 (p) = V(p) ∪ V
⋆ (p); for all w ∈ W, \(\preceq _{w}^{\mathcal {N}}\,=\,\preceq _{w}\cup \,\{\langle v,u\rangle \mid v\in W^{\mathcal {N}}~\mathrm { and }~u\in W^{\star }\}\); for all \(w^{\star }\in W^{\star }\), \(\preceq _{w^{\star }}^{\mathcal {N}}\,=\,\preceq _{w^{\star }}\cup \, \{\langle v,u\rangle \mid v\in W^{\mathcal {N}}~\mathrm { and }~u\in W\}\). In other words, 𝒩 is the result of first taking the disjoint union of ℳ and ℳ
⋆ (so there are no v ∈ W and u ∈ W
⋆ such that v ⇾𝒩
u or u ⇾𝒩
v) and then making all worlds in \(W^{\star }\) the least relevant worlds from the perspective of all worlds in W , and vice versa.Footnote 44 Given this construction, it is easy to prove by induction that for all w ∈ W and formulas φ, \(\mathcal {M},w\vDash _{d}\varphi \) iff \(\mathcal {N},w\vDash _{d}\varphi \) iff \(\mathcal {N},w^{\star }\vDash _{d}\varphi \). Moreover, ⇾𝒩 is an equivalence relation if ⇾ is.
Next we turn 𝒩 into a model with universal fields, without changing ⇾𝒩. Suppose that for w, v ∈ W, v is not in the field of \(\preceq _{w}^{\mathcal {N}}\), which is the case iff v
⋆ is not in the field of \(\preceq _{w^{\star }}^{\mathcal {N}}\). (Remember that for all w ∈ W and \(u\in W^{\star }\), u is in the field of \(\preceq _{w}^{\mathcal {N}}\) and vice versa). Let 𝒩′ = 〈W′, ⇾′, ≤′, V′〉 be such that: \(W'=W^{\mathcal {N}}\); ⇾′ = ⇾𝒩; \(V'=V^{\mathcal {N}}\); for all \(u\in W'\setminus \{w,w^{\star }\}\), \(\preceq _{u}'\,=\,\preceq _{u}^{\mathcal {N}}\); \(\preceq _{w}'=\,\preceq _{w}^{\mathcal {N}}\cup \,\{\langle x, v\rangle \mid x\in W_{w}^{\mathcal {N}}\cup \{v\}\}\); and \(\preceq _{w^{\star }}'=\,\preceq _{w^{\star }}^{\mathcal {N}}\cup \,\{\langle x, v^{\star }\rangle \mid x\in W_{w^{\star }}^{\mathcal {N}}\cup \{v^{\star }\}\}\). It follows that for all \(x\in W_{w}^{\mathcal {N}}\), \(x\preceq _{w}' v^{\star }\prec _{w}' v\); and for all \(x\in W_{w^{\star }}^{\mathcal {N}}\), \(x\preceq _{w^{\star }}' v\prec _{w^{\star }}' v^{\star }\). Since  and
and  , one can prove by induction that for all φ and \(u\in W\), \(\mathcal {N},u\vDash _{d}\varphi \) iff \(\mathcal {N}',u\vDash _{d}\varphi \) iff \(\mathcal {N}',u^{\star }\vDash _{d}\varphi \). The key is that although we put v in the field of \(\preceq '_{w}\), this cannot make any \(K\psi \) formula that is true at \(\mathcal {N},w\) false at \(\mathcal {N}',w\), for if \(\mathcal {N}',v\nvDash _{d}\psi \), then by the inductive hypothesis \(\mathcal {N}',v^{\star }\nvDash _{d}\psi \), and \(v^{\star }\) is more relevant than v and eliminated at w; similarly, although we put \(v^{\star }\) in the field of \(\preceq '_{w^{\star }}\), this cannot make any \(K\psi \) formula that is true at \(\mathcal {N},w^{\star }\) false at \(\mathcal {N}',w^{\star }\). Applying the transformation \(\mathcal {N}\mapsto \mathcal {N}'\) successively no more than \(|W^{\mathcal{N}}|^2\) times with other worlds like w and v yields a universalized \(\mathcal {M}^{u}\). □
, one can prove by induction that for all φ and \(u\in W\), \(\mathcal {N},u\vDash _{d}\varphi \) iff \(\mathcal {N}',u\vDash _{d}\varphi \) iff \(\mathcal {N}',u^{\star }\vDash _{d}\varphi \). The key is that although we put v in the field of \(\preceq '_{w}\), this cannot make any \(K\psi \) formula that is true at \(\mathcal {N},w\) false at \(\mathcal {N}',w\), for if \(\mathcal {N}',v\nvDash _{d}\psi \), then by the inductive hypothesis \(\mathcal {N}',v^{\star }\nvDash _{d}\psi \), and \(v^{\star }\) is more relevant than v and eliminated at w; similarly, although we put \(v^{\star }\) in the field of \(\preceq '_{w^{\star }}\), this cannot make any \(K\psi \) formula that is true at \(\mathcal {N},w^{\star }\) false at \(\mathcal {N}',w^{\star }\). Applying the transformation \(\mathcal {N}\mapsto \mathcal {N}'\) successively no more than \(|W^{\mathcal{N}}|^2\) times with other worlds like w and v yields a universalized \(\mathcal {M}^{u}\). □
5.2.3 Finite Models and Complexity
From the proofs of Section 5.2.2, we obtain results on finite models and the complexity of satisfiability for D-semantics over total (linear, universal) RA models.
Corollary 5.24 (Effective Finite Model Property)
For any formula φ of the epistemic language, if φ is satisfiable in a total RA model according to D-semantics, then φ is satisfiable in a total RA model ℳ with \(|\mathcal {M}| \leq |\varphi |^{d(\varphi )}\).
Proof
By strong induction on \(d(\varphi )\). Since φ is satisfiable iff \(\neg \varphi \) is falsifiable, consider the latter. By Proposition 5.16, \(\neg \varphi \) is equivalent to a conjunction of T-unpacked formulas of the form χ n, m , which is falsifiable iff one of its conjuncts χ n, m is falsifiable. By Lemmas 5.19–5.22, if χ n, m is falsifiable, then it is falsifiable in a model ℳ that combines at most k other models (and one root world), where k is the number of top-level K operators in χ n, m , which is bounded by \(|\varphi |\). Each of the these models is selected as a model of a formula of lesser modal depth than χ n, m , so by the inductive hypothesis we can assume that each is of size at most \(|\varphi |^{d(\varphi )-1}\). Hence \(|\mathcal {M}|\leq |\varphi |\times |\varphi |^{d(\varphi )-1}= |\varphi |^{d(\varphi )}\). □
Corollary 5.25 (Complexity of Satisfiability)
-
1.
The problem of deciding whether an epistemic formula is satisfiable in the class of total RA models according to D-semantics is in PSPACE;
-
2.
For any k, the problem of deciding whether an epistemic formula φ with \(d(\varphi )\leq k\) is satisfiable in the class of total RA models according to D-semantics is NP-complete.
Proof
(Sketch) For part 1, given PSPACE = NPSPACE (see Papadimitriou [59, Section 7.3]), it suffices to give a non-deterministic algorithm using polynomial space. By the previous results (including Prop. 5.16), if φ is satisfiable, then it is satisfiable in a model that can be inductively constructed as in the proofs of Lemmas 5.19, 5.21, and 5.22. We want an algorithm to non-deterministically guess such a model. However, since the size of the model may be exponential in |φ|, we cannot necessarily store the entire model in memory using only polynomial space. Instead, we non-deterministically guess the submodels that are combined in the inductive construction, taking advantage of the following fact from the proof of Lemma 5.19. Once we have computed the truth values at 𝒩, v (or 𝒪, u) of all subformulas of φ (up to some modal depth, depending on the stage of the construction), we can label v with the true subformulas and then erase the rest of 𝒩 from memory (and similarly for 𝒪, u). The other worlds in 𝒩 will not be in the field of ⪯ x for any world x at which we need to compute truth values at any later stage of the construction, so it is not necessary to access those worlds in order to compute later truth values. Given this space-saving method, we only need to use polynomial space at any given stage of the algorithm. I leave the details of the algorithm to the reader.Footnote 45
For part 2, NP-hardness is immediate, since for k = 0 we have all formulas of propositional logic. For membership in NP, if φ is satisfiable and d(φ) ≤ k, then by Corollary 5.24, φ satisfiable in a model ℳ with |ℳ| ≤ |φ|k. We can non-deterministically guess such a model, and it is easy to check that evaluating φ in ℳ is in polynomial time given that ℳ is polynomial-sized. □
As explained in Remark 7.2, Corollary 5.25.1 accords with results of Vardi [72]. Corollary 5.25.2 accords with results of Halpern [28] on the effect of bounding modal depth on the complexity of satisfiability for modal logics.
5.3 Completeness for All RA Models
Next we prove the ‘only if’ direction of Theorem 5.2.3. In the process we prove the separation property for D-semantics over all RA models noted in Proposition 5.6. Interestingly, dropping totality makes things simpler.
Claim
If neither (a) nor (d) holds for a T-unpacked χ n, m , then there is a pointed RA model ℳ, w such that \(\mathcal {M},w\nvDash _{d}\chi _{n,m}\).
Proof
If \(m\leq 1\), (d) is the same as (c), covered in Section 5.2.2. So suppose \(m >1\). By Lemma 5.22 and the \(m=1\) case of the inductive proof of Lemma 5.21, if neither (a) nor (d) holds for χ n, m , then for all \(1\leq j\leq m\), there is a linear RA model ℳ j = 〈w j , ⇾ j , ≤ j , V j 〉 with point \(w_{j}\in W_{j}\) such that
Recall that \(\mathcal {M}_{j}\) is constructed in such a way that for all \(v\in W_{j}^-=W_{j} \setminus \{w_{j}\}\), \(w_{j}\) is not in the field of \(\preceq ^{j}_{v}\). Without loss of generality, assume that for all \(j,k\leq m\), \(W_{j}\cap W_{k}=\emptyset \). Construct ℳ = 〈W, ⇾, ≤,V〉 as follows, by first taking the disjoint union of all of the \(\mathcal {M}_{j}\), then “merging” all of the \(w_{j}\) into a single new world w (with the same valuation as some \(w_{k}\)), so that the linear models \(\mathcal {M}_{j}\) are linked to w like spokes to the hub of a wheel (recall Fig. 3):

It is easy to verify that for all formulas \(\xi \), \(j\leq m\), and \(v\in W_{j}^-\),
It follows from the construction of ℳ and ((5.28)) that for all \(j\leq m\),

, given \(\mathcal {M}_{j},w_{j}\nvDash _{d} K\psi _{j}\) by assumption, the left side of (5.29) is nonempty, so the right side is nonempty. Hence by the truth definition,
By our initial assumption, for all \(j\leq m\),

We prove by induction that for \(1\leq i \leq n\),

Base Case
Given ℳ 1, w 1 ⊨ φ 0 and the fact that w has the same valuation under V as w 1 under V 1, we have ℳ 1, w ⊨ φ 0. Together with (5.30), this implies ℳ 1, w ⊭ d χ 0,m . Since χ 1,m is T-unpacked, it follows by Definition 5.15 that ℳ, w ⊨ d φ 1, in which case \(w\not \in ~ \text {Min}_{\preceq _{w}}\left(\overline {\left[\left[ \varphi _{1}\right]\right] }^{\mathcal {M}}\right)\). By construction of ℳ, together (5.31), (5.28), and \(w\not \in ~ \text {Min}_{\preceq _{w}}\left(\overline {\left[\left[ \varphi _{1}\right]\right] }^{\mathcal {M}}\right)\) imply (5.32) for \(i=1\).
Inductive Step
Assume (5.32) for all k ≤ i (i < n), so ℳ, w ⊨ d Kφ 1 ∧ ⋯ ∧ Kφ 1, which with (5.30) gives ℳ, w ⊭ d χ i,m . Then since χ i+1,m is T-unpacked, ℳ, w ⊨ d φ i+1, so by reasoning as in the base case, (5.32) holds for i + 1.
Since (5.32) holds for 1 ≤ i ≤ n, by the truth definition we have ℳ, w ⊨ d K φ 1 ∧ ⋯ ∧ K φ n , which with ℳ, w ⊨φ 0 and (5.30) implies \(\mathcal {M},w\nvDash _{d} \chi _{n,m}\). □
A remark analogous to Remark 5.20 applies to the above construction: if each ⇾ j is an equivalence relation and we extend ⇾ to the minimal equivalence relation ⇾+ ⊇ ⇾, then the resulting model will still falsify χ n, m . Hence Theorem 5.2.3 holds for the class of RA models with equivalence relations (and with the universal field property by Prop. 5.23). Finally, arguments similar to those of Corollaries 5.24–5.25 show the finite model property and PSPACE satisfiability without the assumption of totality (see Remark 7.2).
5.4 Completeness for CB Models
Finally, for the ‘only if’ direction of Theorem 5.2.4, there are two ways to try to falsify some χ n, m . For H/N-semantics, we can first construct an RA countermodel for χ n, m under D-semantics, as in Section 5.2, and then transform it into a CB countermodel for χ n, m under H/N-semantics, as shown in Section 6 below. Alternatively, we can first construct a CB countermodel under S/H-semantics and then transform it into a CB countermodel under H/N-semantics as in Section 6. Here we will take the latter route. By Proposition 6.2 below, for the ‘only if’ direction of Theorem 5.2.4 it suffices to prove the following.
Claim
If neither (a) nor (d) holds for a flat, T-unpacked χ n, m , then there is a pointed CB model ℳ, w such that ℳ, w ⊭ h,s χ n,m .
We begin with some notation used in the proof and in later sections.
Notation 5.26 (Relational Image) Given a CB model ℳ = 〈W, D, ≤, V〉, the image of {w} under the relation D is D(w) = {v ∈ W | wDv}.
Hence D(w) is the set of doxastically accessible worlds for the agent in w.
Let us now prove the claim.
Proof
For any positive integer z, let \(P_{z}=\{1,\dots ,z\}\). For all \(k\in P_{m}\), let \(S_{k}=\{i\in P_{n}\mid \;\vDash \psi _{k}\rightarrow \varphi _{i} \}\), and \(T=\{t\in P_{m}\mid S_{t} = P_{n}\}\). Since (d) does not hold for χ n, m , it follows that
Construct ℳ = 〈W, D, ≤ ,V〉 as follows (see Fig. 6):
$$W=\{w\}\cup\{x_{t}\mid t\in T\} \cup \{v_{k},u^{k}_{j}\mid k\in P_{m} \setminus T~\mathrm{and}~j\in P_{n} \setminus S_{k}\}; $$D is the union of \(\{\langle w,w\rangle \}\), \(\{\langle w,x_{t}\rangle , \langle x_{t},x_{t}\rangle \mid t\in T\}\), and
$$\left\{\langle v_{k},u^{k}_{j} \rangle, \langle u^{k}_{j},u^{k}_{j}\rangle \mid k\in P_{m} \setminus T~\mathrm{and}~j\in P_{n}\setminus S_{k}\right\}; $$\(\leqslant _{w} \,=\{\langle w,w\rangle \}\cup \{\langle w,v_{k}\rangle , \langle v_{k}, w\rangle , \langle v_{k}, v_{k}\rangle \mid k\in P_{m} \}\);Footnote 46
For y ∈ W ∖ {w}, ≤ y is any relation as in Definition 3.1.3;
V is any valuation function on W such that ℳ, w ⊨ φ0 and
for all t ∈ T, \(\mathcal {M},x_{t}\vDash \underset {i \in P_{n}}{\bigwedge }\varphi _{i}\wedge \neg \psi _{t}\);
for all \(k \in P_{m}\setminus T\), \(\mathcal {M},v_{k}\vDash \underset {i \in S_{k}}{\bigwedge }\varphi _{i}\wedge \neg \psi _{k}\);
for all \(k\in P_{m}\setminus T\) and \(j\in P_{n}\setminus S_{k}\), \(\mathcal {M},u_{j}^{k}\vDash \neg \varphi _{j}\wedge \psi _{k}\).
Such a valuation V exists by the assumption that (a) does not hold for χ n, m , together with (5.33) and the definitions of T and \(S_{k}\).
Since χ n, m is flat and T-unpacked, \(\mathcal {M},w\vDash \varphi _{0}\) implies \(\mathcal {M},w\vDash \varphi _{1}\wedge \dots \wedge \varphi _{n}\). Then since \(D(w)=\{w\}\cup \{x_{t}\mid t\in T\}\) and \(\mathcal {M},x_{t}\vDash \varphi _{1}\wedge \dots \wedge \varphi _{n}\) for all \(t\in T\),
For all \(k \in P_{m}\setminus T\), we have
given \(v_{k} Du^{k}_{j}\) and \(\mathcal {M},u^{k}_{j}\nvDash \varphi _{j}\), and
by definition of V. It follows from (5.35) and (5.36) that for all \(k \in P_{m}\setminus T\),
By construction of ℳ, (5.34) and 5.37 together imply that for all \(y\in W_{w}\),
Together (5.34) and (5.38) imply \(\mathcal {M},w\vDash _{h,s} K\varphi _{i}\) for all \(i\in P_{n}\) by the truth definitions (Def. 4.3). Now let us check that \(\mathcal {M},w\nvDash _{h,s} K\psi _{i}\) for all \(i\in P_{m}\). On the one hand, for all \(t\in T\), given \(wDx_{t}\) and \(\mathcal {M},x_{t}\nvDash \psi _{t}\), we have \(\mathcal {M},w\nvDash B\psi _{t}\) and hence \(\mathcal {M},w\nvDash _{h,s} K\psi _{t}\). On the other hand, for all \(k\in P_{m}\setminus T\), given \(D(v_{k})=\{u^{j}_{k}\mid j \in P_{n}\setminus S_{k}\}\) and \(\mathcal {M},u_{j}^{k}\vDash \psi _{k}\), we have \(\mathcal {M},v_{k}\vDash B\psi _{k}\); but then since \(\mathcal {M},v_{k}\nvDash \psi _{k}\) and \(v_{k}\in ~\text {Min}_{\leqslant _{w}}(W)\), it follows that \(\mathcal {M},w\nvDash _{h,s} K\psi _{k}\). Together with \(\mathcal {M},w\vDash \varphi _{0} \), the previous facts imply \(\mathcal {M},w\nvDash _{h,s} \chi _{n,m}\). □
We leave the extension of the ‘only if’ direction of Theorem 5.2.4 to the full epistemic language for other work (see Problem 8.12). Facts 8.8.4, 8.8.5, and 8.10.1 show that for the full language, this direction must be modified. Yet for our purposes here, the above proof already helps to reveal the sources of closure failure in H/S-semantics and in N-semantics by Proposition 6.2 below.
5.5 The Sources of Closure Failure
The results of Sections 5.2–5.4 allow us to clearly identify the sources of closure failure in D/H/N/S-semantics. In D-semantics, the source of closure failure is the orderings—if we collapse the orderings, then D- is equivalent to L-semantics (see Observation 8.3) and closure failures disappear. By Proposition 6.1 below, the orderings are also a source of closure failure in H/N-semantics. However, the proof in Section 5.4 shows that there is another source of closure failure in H/N/S-semantics: the interpretation of ruling out in terms belief , as in the quote from Heller in Section 3. This is the sole source of closure failure in S-semantics, the odd member of the D/H/N/S-family that does not use the orderings beyond \(\text {Min}_{\leqslant _{w}}(W)\) (recall Observation 4.5). Given this source of closure failure, even if we collapse the orderings, in which case H- is equivalent to S-semantics (see Prop. 6.3), closure failure persists. We will return to this point in Section 9.
6 Relating RA and CB Models
The discussion in Sections 5.4 and 5.5 appealed to claims about the relations between D/H/N/S-semantics. In this short section, we prove these claims. Readers eager to see how the results of Section 5 lead to complete deductive systems for the RA and subjunctivist theories should skip ahead to Section 7 and return here later.
One way to see how the RA and subjunctivist theories are related is by transforming models viewed from the perspective of one theory into models that are equivalent, with respect to what can be expressed in our language, when viewed from the perspective of another theory. This also shows that any closure principle that fails for the first theory also fails for the second.
We first see how to transform any RA model viewed from the perspective of D-semantics into a CB model that is equivalent, with respect to the flat fragment of the epistemic language, when viewed from the perspective of H-semantics. The transformation is intuitive: if, in the RA model, a possibility v is eliminated by the agent in w, then we construct the CB model such that if the agent were in situation v instead of w, the agent would notice, i.e., would correctly believe that the true situation is v rather than w;Footnote 47 but if, in the RA model, v is uneliminated by the agent in w, then we construct the CB model such that if the agent were in situation v instead of w, the agent would not notice, i.e., would incorrectly believe that the true situation is w rather than v. (The CB model in Fig. 2 is obtained from the RA model in Fig. 1 in this way). Then the agent has eliminated the relevant alternatives to a flat φ at w in the RA model iff the agent sensitively believes φ at w in the CB model.
Proposition 6.1 (D-to-H Transform)
For any RA model ℳ = 〈W, ⇾, ≤, W〉 with w ∈ W, there is a CB model \(\mathcal {N}=\left \langle W,D,\leqslant ,V\right \rangle \) such that for all flat epistemic formulas φ,
Proof
Construct 𝒩 from ℳ as follows. Let W and V in 𝒩 be the same as in ℳ; let \(\leqslant \) in 𝒩 be the same as ≤ in ℳ; construct D in 𝒩 from ⇾ in ℳ as follows, where w is the fixed world in the lemma (recall Notation 5.26):

To prove the ‘iff’ by induction on φ, the base case is immediate and the boolean cases routine. Suppose φ is of the form \(K\psi \). Since φ is flat, ψ is propositional. Given that V is the same in 𝒩 as in ℳ, for all \(v\in W\), \(\mathcal {M},v\vDash _{d}\psi \) iff \(\mathcal {N},v\vDash _{h}\psi \). Hence if \(\mathcal {M},w\nvDash _{d}\psi \), then \(\mathcal {M},w\nvDash _{d} K\psi \) and \(\mathcal {N},w\nvDash _{h} K\psi \) by Facts 3.7 and 4.4. Suppose \(\mathcal {M},w\vDash _{d}\psi \). Since w ⇾ w, we have \(D(w)=\{w\}\) by construction of 𝒩, so \(\mathcal {N},w\vDash _{h} B\psi \) given \(\mathcal {N},w\vDash _{h}\psi \). It only remains to show that \(\mathcal {M},w\vDash _{d} K\psi \) iff the sensitivity condition (Def. 4.3) for \(K\psi \) is satisfied at \(\mathcal {N},w\). This is easily seen to be a consequence of the following, given by the construction of 𝒩:

The left-to-right direction of the biconditional in (6.3) follows from the fact that if w ⇾ u, then \(D(u)=\{w\}\), and \(\mathcal {N},w\vDash _{h}\psi \). For the right-to-left direction, if  , then \(D(u)=\{u\}\), in which case \(\mathcal {N},u\nvDash _{h} B\psi \) given \(\mathcal {N},u\nvDash _{h} \psi \). □
, then \(D(u)=\{u\}\), in which case \(\mathcal {N},u\nvDash _{h} B\psi \) given \(\mathcal {N},u\nvDash _{h} \psi \). □
The transformation above does not always preserve all non-flat epistemic formulas, and by Fact 8.8.4, no transformation does so. However, since the flat fragment of the language suffices to express all principles of closure with respect to propositional logic, Proposition 6.1 has the notable corollary that all such closure principles that fail in D-semantics also fail in H-semantics.
Next we transform CB models viewed from the perspective of H-semantics into CB models that are equivalent, with respect to the epistemic-doxastic language, when viewed from the perspective of N-semantics. (Fact 8.8 in Section 8 shows that there is no such general transformation in the N-to-H direction.) To do so, we make the models centered, which (as noted in Observation 4.5) trivializes the adherence condition that separates N- from H-semantics.
Proposition 6.2 (H-to-N Transform)
For any CB model \(\mathcal {N}=\left \langle W,D,\leqslant ,V\right \rangle \), there is a CB model \(\mathcal {N'}=\left \langle W,D,\leqslant ',V\right \rangle \) such that for all w ∈ W and all epistemic-doxastic formulas φ,
Proof
Construct \(\mathcal {N}'\) from 𝒩 as follows. Let W , D, and V in \(\mathcal {N}'\) be the same as in 𝒩. For all w ∈ W, construct \(\leqslant _{w}'\) from ≤ w by making w strictly minimal in \(\leqslant '_{w}\), but changing nothing else:
To prove the proposition by induction on φ, the base case is immediate and the boolean and belief cases routine. Suppose φ is \(K\psi \) and \(\left[\left[ \psi \right]\right] _{h}^{\mathcal {N}}=\left[\left[ \psi \right]\right] _{n}^{\mathcal {N}'}\). If \(\mathcal {N},w\nvDash _{h}\psi \), then \(\mathcal {N},w\nvDash _{h} K\psi \) and \(\mathcal {N}',w\nvDash _{n} K\psi \) by Fact 4.4. If \(\mathcal {N},w\vDash _{h}\psi \) and hence \(\mathcal {N}',w\vDash _{n}\psi \), then by construction of \(\leqslant _{w}'\) and the inductive hypothesis,
Since D is the same in 𝒩 as in \(\mathcal {N}'\), (6.5) implies that the belief and sensitivity conditions for \(K\psi \) are satisfied at \(\mathcal {N},w\) iff they are satisfied at \(\mathcal {N}',w\). If the belief condition is satisfied, then \(\text {Min}_{\leqslant '_{w}}(\left[\left[ B\psi \right]\right] _{n}^{\mathcal {N}'})=\{w\}\) by construction of \(\leqslant _{w}'\), so the adherence condition (Def. 4.3) is automatically satisfied at \(\mathcal {N}',w\). Hence the belief and sensitivity conditions for \(K\psi \) are satisfied at \(\mathcal {N},w\) iff the belief, sensitivity, and adherence conditions are satisfied for \(K\psi \) at \(\mathcal {N}',w\).Footnote 48 □
Our last transformation takes us from models viewed from the perspective of S-semantics to equivalent models viewed from the perspective of H-semantics—and hence N-semantics by Proposition 6.2. (Fact 8.10 in Section 8 shows that there can be no such general transformation in the H-to-S direction.) The idea of the transformation is that safety is the ∃∀ condition (as in Section 3) obtained by restricting the scope of sensitivity to a fixed set of worlds, \(\text {Min}_{\leqslant _{w}}(W)\).
Proposition 6.3 (S-to-H Transform)
For any CB model \(\mathcal {N}=\left \langle W,D,\leqslant ,V\right \rangle \), there is a CB model \(\mathcal {N'}=\left \langle W,D,\leqslant ',V\right \rangle \) such that for all w ∈ W and all epistemic-doxastic formulas φ,
Proof
Construct \(\mathcal {N}'\) from 𝒩 as follows. Let W , D, and V in \(\mathcal {N}'\) be the same as in 𝒩. For all w ∈ W, construct \(\leqslant _{w}'\) from ≤ w by taking \(\text {Min}_{\leqslant _{w}}(W)\) to be the field of \(\leqslant _{w}'\) and setting \(u\leqslant _{w} ' v\) for all u and v in the field. It is straightforward to check that 𝒩 and \(\mathcal {N'}\) are equivalent with respect to the safety condition and that in \(\mathcal {N}'\) the safety and sensitivity conditions become equivalent.Footnote 49 □
Although I have introduced the propositions above for the purpose of relating the (in)valid closure principles of one theory to those of another, by transforming countermodels of one kind into countermodels of another, the interest of this style of analysis is not just in transferring principles for reasoning about knowledge between theories; the interest is also in highlighting the structural relations between different pictures of what knowledge is. In part II, we will continue our model-theoretic analysis to illuminate these pictures.
7 Deductive Systems
From Theorem 5.2 we obtain complete deductive systems for reasoning about knowledge according to the RA, tracking, and safety theories. Table 1 lists all of the needed schemas and rules, using the nomenclature of Chellas [12] (except for X, RAT, and RA, which are new). E is the weakest of the classical modal systems with PL, MP, and RE. ES 1…ES n is the extension of E with every instance of schemas S 1…S n . EMCN is familiar as the weakest normal modal system K, equivalently characterized in terms of PL, MP, the K schema, and the necessitation rule for K (even more simply, by PL, MP, and RK).
Corollary 7.1 (Soundness and Completeness)
-
1.
The system KT (equivalently, ET plus the RK rule) is sound and complete for C/L-semantics over RA models.
-
2.
(The Logic of Ranked Relevant Alternatives) The system ECNTX (equivalently, ET plus the RAT rule) is sound and complete for D-semantics over total RA models.
-
3.
The system ECNT (equivalently, ET plus the RA rule) is sound and complete for D-semantics over RA models.
-
4.
ECNT is sound (with respect to the full epistemic language) and complete (with respect to the flat fragment) for H/N/S-semantics over CB models.Footnote 50
The proof of Corollary 7.1 is similar to the alternative completeness proof discussed by van Benthem [8, Section 4.3] for the system K.Footnote 51
Proof
We only give the proof for part 2, since the proofs for the others are similar. Soundness follows from Theorem 5.2.2. For completeness, we first prove by strong induction on the modal depth \(d(\varphi )\) of φ (Def. 2.2) that if φ is D-valid over total RA models, then φ is provable in the system combining ET and the RAT rule. If \(d(\varphi )=0\), then the claim is immediate, since our deductive system includes propositional logic. Suppose \(d(\varphi )=n+1\). By the proof of Proposition 5.16, using PL, MP, T, and RE (which is a derived rule given RAT, PL, and MP), we can prove that φ is equivalent to a conjunction \(\varphi '\), each of whose conjuncts is a T-unpacked formula (Def. 5.15) of the form
The conjunction \(\varphi '\) is valid iff each conjunct of the form of (7.1) is valid. By Theorem 5.2.2, (7.1) is valid iff either condition (a) or condition (c) of Theorem 5.2.2 holds. Case 1: (a) holds, so \(\varphi _{0}\rightarrow \bot \) is valid. By the inductive hypothesis, we can derive \(\varphi _{0}\rightarrow \bot \), from which we derive (7.1) using PL and MP. Case 2: (c) holds, so for some \(\Phi \subseteq \{\varphi _{1},\dots ,\varphi _{n}\}\) and nonempty \(\Psi \subseteq \{\psi _{1},\dots ,\psi _{m}\}\),
is valid. Since (7.2) is of modal depth less than \(n+1\), by the inductive hypothesis it is provable. From (7.2), we can derive
using the RAT rule, from which we can derive (7.1) using PL and MP. Having derived each conjunct of \(\varphi '\) in one of these ways, we can use PL and MP to derive the conjunction itself, which by assumption is provably equivalent to φ.
Next we show by induction on the length of proofs that any proof in the system combining ET and RAT can be transformed into an ECNTX proof of the same theorem. Suppose that in the first proof, \(\varphi _{1}\wedge \dots \wedge \varphi _{n}\leftrightarrow \psi _{1}\wedge \dots \wedge \psi _{m}\) has been derived, to which the RAT rule is applied. In the second proof, if \(n> 0\), we first derive \(K\varphi _{1}\wedge \dots \wedge K\varphi _{n} \rightarrow K(\varphi _{1}\wedge \dots \wedge \varphi _{n})\) using C repeatedly (with PL and MP); next, we derive \(K(\varphi _{1}\wedge \dots \wedge \varphi _{n})\leftrightarrow K(\psi _{1}\wedge \dots \wedge \psi _{m})\) by applying the RE rule to \(\varphi _{1}\wedge \dots \wedge \varphi _{n}\leftrightarrow \psi _{1}\wedge \dots \wedge \psi _{m}\); we then derive \(K(\psi _{1}\wedge \dots \wedge \psi _{m})\rightarrow K\psi _{1}\vee \dots \vee K\psi _{m}\) using X repeatedly (with PL and MP); finally, we derive \(K\varphi _{1}\wedge \dots \wedge K\varphi _{n} \rightarrow K\psi _{1}\vee \dots \vee K\psi _{m}\) using PL, MP, and earlier steps. If \(n=0\),Footnote 52 we first derive \(K\top \) using N, then derive \(K\top \leftrightarrow K(\psi _{1}\wedge \dots \wedge \psi _{m})\) by applying the RE rule to \(\top \leftrightarrow \psi _{1}\wedge \dots \wedge \psi _{m}\), then derive the conclusion of the RAT application using X, PL, and MP. □
For reasons suggested in Section 5.2, I do not consider the systems of Corollary 7.1.2–.4 to be plausible as epistemic logics, and therefore I do not consider the basic theories they are based on to be satisfactory theories of knowledge. Nonetheless, we may wish to reason directly about whether one has ruled out the relevant alternatives, whether one’s beliefs are sensitive to the truth, etc., and Corollary 7.1 gives principles for these notions. Simply replace the K symbol by a neutral □ and the newly identified logic ECNTX, which I dub the logic of ranked relevant alternatives, is of significant independent interest.
With these qualifications in mind, I will make another negative point concerning knowledge. It is easy to derive the K axiom, the star of the epistemic closure debate with its leading role in skeptical arguments, from M, C, RE, and propositional logic. Hence in order to avoid K one must give up one of the latter principles. (For RE, recall that we are considering ideally astute logicians as in Section 2). What is so strange about subjunctivist-flavored theories is that they validate C but not M, which seems to get things backwards. Hawthorne [32, Sections 1.6, 4.6] discusses some of the problems and puzzles, related to the Lottery and Preface Paradoxes (Kyburg [46]; Makinson [54]), to which C leads (also see Goldman [25]). M seems rather harmless by comparison (cf. Williamson [78, Section 12.2]). Interestingly, C also leads to computational difficulties.
Remark 7.2 (NP vs. PSPACE)
Vardi [72] proved a PSPACE upper bound for the complexity of the system ECNT,Footnote 53 in agreement with our conclusion in Section 5.3. (Together Corollaries 5.25 and 7.1.2 give a PSPACE upper bound for ECNTX.) Vardi also conjectured a PSPACE lower bound for ECNT. By contrast, he showed that for any subset of \(\{\mathrm {T}, \mathrm {N}, \mathrm {M}\}\) added to E, complexity drops to NP-complete. Hence Vardi conjectured that the C axiom is the culprit behind the jump in complexity of epistemic logics from NP to PSPACE.Footnote 54 It appears that not only is C more problematic than M epistemologically, but also it makes reasoning about knowledge more computationally costly.Footnote 55
8 Higher-Order Knowledge
In this section, we briefly explore how the theories formalized in Sections 3 and 4 differ with respect to knowledge about one’s own knowledge and beliefs. The result is a hierarchical picture (Corollary 8.12) and an open problem for future research. First, we discuss a subtlety concerning higher-order RA knowledge. Second, we relate properties of higher-order subjunctivist knowledge to closure failures.
8.1 Higher-Order Knowledge and Relevant Alternatives
Theorem 5.2 and Corollary 7.1 show that no non-trivial principles of higher order knowledge, such as the controversial 4 axiom Kφ → Kφ and 5 axiom ¬Kφ → K¬Kφ, are valid over RA models according to either L- or D-semantics. This is so even if we assume that the relation ⇾ in our RA models is an equivalence relation (see Remark 5.20), following Lewis [52].
Example 8.1 (Failure of 4 Axiom)
For the model ℳ in Fig. 7, in which ⇾ is an equivalence relation, observe that ℳ, w
1 ⊭
l,d
Kp → KKp. Since \(\text {Min}_{\preceq _{w_{1}}}(W)\cap \overline {\left[\left[ p\right]\right] }=\{w_{2}\}\) and  , we have ℳ, w
1 ⊨
l,d
Kp. By contrast, since \(w_{4}\in ~\text {Min}_{\preceq _{w_{3}}}(W)\cap \overline {\left[\left[ p\right]\right] }\) and w
3 ⇾ w
4, we have ℳ, w
3 ⊭
l,d
Kp. It follows that \(w_{3}\in ~\text {Min}_{\preceq _{w_{1}}}(W)\cap \overline {\left[\left[ Kp\right]\right] }\), in which case ℳ, w
1 ⊭
l,d
KKp given w
1 ⇾ w
3.
, we have ℳ, w
1 ⊨
l,d
Kp. By contrast, since \(w_{4}\in ~\text {Min}_{\preceq _{w_{3}}}(W)\cap \overline {\left[\left[ p\right]\right] }\) and w
3 ⇾ w
4, we have ℳ, w
3 ⊭
l,d
Kp. It follows that \(w_{3}\in ~\text {Min}_{\preceq _{w_{1}}}(W)\cap \overline {\left[\left[ Kp\right]\right] }\), in which case ℳ, w
1 ⊭
l,d
KKp given w
1 ⇾ w
3.
According to Williamson [79, 80], “It is not always appreciated that…since Lewis’s accessibility relation is an equivalence relation, his account validates not only logical omniscience but the very strong epistemic logic S5” [80, 23n16]. However, Example 8.1 shows that this is not the case if we allow that comparative relevance, like comparative similarity, is possibility-relative, as seems reasonable for a Lewisian theory.Footnote 56 Other RA theorists are explicit that relevance depends on similarity of worlds (see, e.g., Heller [33, 35]), in which case the former should be world-relative since the latter is. For Williamson’s point to hold, we would have to block the likes of Example 8.1 with an additional constraint on our models, such as the following.
Definition 8.2 (Absoluteness)
For an RA model ℳ = 〈W, ⇾, ≤, V〉, ≤ is locally (resp. globally) absolute iff for all w ∈ W and v ∈ W w (resp. for all \(w,v\in W\)), \(\preceq _{w}\, = \,\preceq _{v}\) [49, Section 6.1].
It is noteworthy that absoluteness leads to a collapse of comparative relevance.
Observation 8.3 (Absoluteness and Collapse)
Given condition 3b of Definition 3.1, if ≤ is locally absolute, then for all w ∈ W and v ∈ W w ,
If ≤ is globally absolute, then for all w ∈ W, \(\text {Min}_{\preceq _{w}}(W)=W\).
Lewis [49, 99] rejected absoluteness for comparative similarity because it leads to such a collapse. We note that with the collapse of comparative relevance, the distinction between L- and D-semantics also collapses.
Observation 8.4 (Absoluteness and Collapse cont.)
Over locally absolute RA models, L- and D-semantics are equivalent.
The proof of Proposition 8.5, which clarifies the issue raised by Williamson, is essentially the same as that of completeness over standard partition models.
Proposition 8.5 (Completeness of S5)
S5 is sound and complete with respect to L/D-semantics over locally absolute RA models in which ⇾ is an equivalence relation.
In general, for locally absolute RA models, the correspondence between properties of ⇾ and modal axioms is exactly as in basic modal logic.
8.2 Higher-Order Knowledge and Subjunctivism
The study of higher-order knowledge becomes more interesting with the subjunctivist theories, especially in connection with our primary concern of closure. According to Nozick [58], the failures of epistemic closure implied by his tracking theory are something that “we must adjust to” (228). This would be easier if problems ended with the closure failures themselves. However, as we will see, the structural features of the subjunctivist theories that lead to these closure failures also lead to problems of higher-order knowledge.
We begin with a definition necessary for stating Fact 8.7 below.
Definition 8.6 (Outer Necessity)
Let us temporarily extend our language with an outer necessity operator □ [49, Section 1.5] with the truth clause:
We call the language with K, B, and □ the epistemic-doxastic-alethic language. Define the possibility operator by \(\Diamond \varphi :=\neg \Box \neg \varphi \), and let \(\hat {K}\varphi :=\neg K\neg \varphi \).
Fact 8.7 below shows that if sensitivity (Def. 4.3) is necessary for knowledge, and if there is any counterfactually accessible world in which an agent believes φ but φ is false, then the agent cannot know that her belief that φ is not false—even if she knows that φ is true.Footnote 57 The proof appears in many places [17, 44, 66, 67, 73, 75].
Fact 8.7 (Possibility and Sensitivity)
\(\Diamond (B\varphi \wedge \neg \varphi )\rightarrow \hat {K}(B\varphi \wedge \neg \varphi )\) is H/N-valid, but not S-valid.
Since \(Kp\wedge \lozenge (Bp\wedge \neg p)\) is satisfiable, \(Kp\rightarrow K \neg (Bp \wedge \neg p)\) is not H/N-valid by Fact 8.7, so \(Kp\rightarrow K (\neg Bp \vee p)\) is not H/N-valid. Hence Fact 8.7 is related to the failure of closure under disjunctive addition. Clearly \(\Diamond \psi \rightarrow \hat {K}\psi \) is not H/N-valid for all ψ. Related to Fact 8.7, Fact 8.8 (used for Corollary 8.12) shows that limited forms of closure, including closure under disjunctive addition, hold when higher-order knowledge of \(B\varphi \rightarrow \varphi \) or \(\hat {K}\varphi \rightarrow \varphi \) is involved.
Fact 8.8 (Higher-Order Closure)
-
1.
\(K(B\varphi \rightarrow \varphi )\rightarrow K((B\varphi \rightarrow \varphi )\vee \psi )\) is H/S-valid, but not N-valid;
-
2.
\(B\varphi \wedge K(B\varphi \rightarrow \varphi )\rightarrow K\varphi \) is H/S-valid, but not N-valid;
-
3.
\(B\varphi \wedge K(\hat {K}\varphi \rightarrow \varphi )\rightarrow K\varphi \) is H/S-valid, but not N-valid;
-
4.
\(K(\varphi \wedge \psi )\wedge K( \hat {K}\varphi \rightarrow \varphi )\rightarrow K\varphi \) is H/S-valid, but not D/N-valid;
-
5.
\(K\varphi \wedge K\psi \wedge K(\hat {K} (\varphi \vee \psi )\rightarrow (\varphi \vee \psi ))\rightarrow K(\varphi \vee \psi )\) is H/N/S-valid, but not D-valid (over total RA models).
While some consider Fact 8.7 to be a serious problem for sensitivity theories, Fact 8.9 seems even worse for subjunctivist-flavored theories in general: according to the ones we have studied, it is possible for an agent to know the classic example of an unknowable sentence, \(p\wedge \neg Kp\) [23]. Williamson [78, 279] observes that \(p\wedge \neg Kp\) is knowable according to the sensitivity theory. We observe that it is also knowable according to the safety theory.Footnote 58
Fact 8.9 (Moore-Fitch Sentences)
K(p ∧ ¬Kp) is satisfiable in RA models under D-semantics and in CB models under H/N/S-semantics.
Proof
It is immediate from Theorem 5.2 that \(\neg K(p\wedge \neg Kp)\) is not D-valid.Footnote 59
We give a simple satisfying CB model ℳ for H/N/S-semantics in Fig. 8. Assume that \(\leqslant _{w_{3}}\) is any appropriate preorder such that ℳ, w 3 ⊨ h,n,s Kp. It will not matter whether \(w_{1}\equiv _{w_{1}} w_{2} \equiv _{w_{1}} w_{3}\) or \(w_{1}\equiv _{w_{1}} w_{2} <_{w_{1}} w_{3}\).
Given \(w_{2}\in ~\text {Min}_{\leqslant _{w_{1}}}(W)\) and \(\mathcal {M},w_{2}\vDash \neg p\wedge Bp\), the safety condition for Kp fails at w 1, so \(\mathcal {M},w_{1}\vDash _{s} p\wedge \neg Kp\). Then since \(D(w_{1})=\{w_{1}\}\) (recall Notation 5.26), \(\mathcal {M},w_{1}\vDash _{s} B(p\wedge \neg Kp)\), so the belief condition for K(p ∧ ¬Kp) holds at w 1. For \(i\geq 2\), given \(\mathcal {M},w_{i}\vDash BKp\), we have \(\mathcal {M},w_{i}\nvDash B(p\wedge \neg Kp)\). It follows that for all \(v\in ~\text {Min}_{\leqslant _{w_{1}}}(W)\), \(\mathcal {M},v\vDash _{s} B(p\wedge \neg Kp)\rightarrow p\wedge \neg Kp\). Hence the safety condition for K(p ∧ ¬Kp) holds at w 1, so \(\mathcal {M},w_{1}\vDash _{s} K(p\wedge \neg Kp)\). One can check that \(\mathcal {M},w_{1}\vDash _{h,n} K(p\wedge \neg Kp)\) as well. For H/N-semantics, the model 𝒩 in Fig. 9, which has the same basic structure as Williamson’s [78, 279] example, also satisfies K(p ∧ ¬Kp) at w 1. Assume \(\leqslant _{w_{2}}\) is any appropriate preorder such that \(\mathcal {N},w_{2}\vDash _{h,n} Kp\).Footnote 60 (Whether \(w_{1}\equiv _{w_{1}}w_{2}\) or \(w_{1}<_{w_{1}}w_{2}\) does not matter). □
It is not difficult to tell a story with the structure of Fig. 8, illustrating that the safety theory allows K(p ∧ ¬Kp), just as Williamson tells a story with the structure of Fig. 9, illustrating that the tracking theory allows it K ( p ∧ ¬ K p ).
Fact 8.9 is related to the fact that closure under conjunction elimination is not valid. Otherwise K(p ∧ ¬Kp) would be unsatisfiable; for by veridicality, \(K(p\wedge \neg Kp)\rightarrow \neg Kp\) is valid, and given closure under conjunction elimination, \(K(p\wedge \neg Kp)\rightarrow Kp\) would also be valid. However, Fact 8.10 shows that K does partially distribute over conjunctions of special forms in S-semantics.
Fact 8.10 (Higher-Order Closure cont.)
-
1.
\(K(\varphi \wedge \neg K\varphi )\rightarrow K\neg K\varphi \) is S-valid, but not D/H/N-valid.
-
2.
\(K ((\varphi \vee \psi )\wedge (B\varphi \rightarrow \varphi ))\rightarrow K(B\varphi \rightarrow \varphi )\) is S-valid, but not H/N-valid.
What Facts 8.9 and 8.7 show is that in order to fully calculate the costs of closure failures, one must take into account their ramifications in the realm of higher-order knowledge. Combining Facts 8.7, 8.8, and 8.10 with results from earlier sections, we arrive at a picture of the relations between the sets of valid principles according to D-, H-, N-, and S-semantics, respectively, given by Corollary 8.12 below.Footnote 61 First we need the following definition.
Definition 8.11 (Theories and Model Classes)
For a class S of models, let \(\text {Th}^{x}_{\mathcal {L}}(\mathsf {S})\) be the set of formulas in the language ℒ that are valid over S according to X-semantics. Let RAT be the class of all total RA models, RA the class of all RA models, and CB the class of all CB models.
Corollary 8.12 (Hierarchies)
-
1.
For the flat fragment ℒ f of the epistemic language,\( Th^{n}_{\mathcal {L}_{f}}(\mathsf {CB}) = Th^{h}_{\mathcal {L}_{f}}(\mathsf {CB}) = Th^{s}_{\mathcal {L}_{f}}(\mathsf {CB}) = Th^{d}_{\mathcal {L}_{f}} (\mathsf {RA})\subsetneq Th^{d}_{\mathcal {L}_{f}}(\mathsf {RAT}). \)
-
2.
For the epistemic language ℒ e , \(Th^{d}_{\mathcal{L}_{e}} (\mathsf{RA}) \subsetneq Th^{n}_{\mathcal{L}_{e}}(\mathsf{CB}) \subsetneq Th^{h}_{\mathcal{L}_{e}}(\mathsf{CB}) \subsetneq Th^{s}_{\mathcal{L}_{e}}(\mathsf{CB}); \\[6pt] Th^{d}_{\mathcal{L}_{e}}(\mathsf{RA}) \subsetneq Th^{d}_{\mathcal{L}_{e}}(\mathsf{RAT})\not\subseteq Th^{s}_{\mathcal{L}_{e}}(\mathsf{CB});\;Th^{n}_{\mathcal{L}_{e}}(\mathsf{CB}) \not\subseteq Th^{d}_{\mathcal{L}_{e}}(\mathsf{RAT}). \)
-
3.
For the epistemic-doxastic language ℒ d ,
$$Th^{n}_{\mathcal{L}_{d}}(\mathsf{CB}) \subsetneq Th^{h}_{\mathcal{L}_{d}}(\mathsf{CB}) \subsetneq Th^{s}_{\mathcal{L}_{d}}(\mathsf{CB}) .$$ -
4.
For the epistemic-doxastic-alethic language ℒ a , \(Th^{n}_{\mathcal{L}_{a}} (\mathsf{CB}) \subsetneq Th^{h}_{\mathcal{L}_{a}} (\mathsf{CB});\; Th^{n}_{\mathcal{L}_{a}} (\mathsf{CB}) \not\subseteq Th^{s}_{\mathcal{L}_{a}} (\mathsf{CB}) \not\subseteq Th^{h}_{\mathcal{L}_{a}} (\mathsf{CB}).\)
Proof
Part 1 follows from Corollary 7.1 and Fact 5.7. Part 2 follows from Corollary 7.1, Propositions 6.2–6.3, and Facts 8.8.5, 8.8.4, 8.10.1, and 5.7. Part 3 follows from Propositions 6.2–6.3 and Facts 8.8 and 8.10. Part 4 follows from Proposition 6.2 (which clearly extends to ℒ a ) and Facts 8.8, 8.7, and 8.10. □
In this section we have focused on the implications of D/H/N/S-semantics for higher-order knowledge, especially in connection with epistemic closure. However, if we take the point of view suggested earlier (Sections 1, 5 and 7), according to which our results can be interpreted as results about desirable epistemic properties other than knowledge, then exploring higher-order phenomena in D/H/N/S-semantics is part of understanding these other properties. Along these lines, we conclude this section with an open problem for future research.
Problem 8.13 (Axiomatization)
Axiomatize the theory of counterfactual belief models according to H-, N-, or S-semantics for the full epistemic, epistemic-doxastic, or epistemic-doxastic-alethic language.Footnote 62
9 Theory Parameters and Closure
In this section, we return to the issue raised in Section 5.5 about the sources of closure failure. Analysis of Theorem 5.2 shows that two parameters of a modal theory of knowledge affect whether closure holds. In Section 3, we identified one: the ∀∃ vs. ∃∀ choice of the relevancy set. Both L- and S-semantics have an ∃∀ setting of this parameter (recall Observation 4.5). However, closure holds in L-semantics but fails in S-semantics. The reason for this is the second theory parameter: the notion of ruling out. With the Lewis-style notion of ruling out in L/D-semantics, a world v is either ruled out at w or not. By contrast, with the notions of ruling out implicit in S/H/N-semantics, we cannot say independently of a proposition in question whether v is ruled out at w.
For example, in the CB model in Fig. 10, v is among the closest worlds to the actual world w. We may say that v is ruled out as an alternative for p ∧ q, in the sense that while p ∧ q is false at v, the agent does not believe p ∧ q at v (but rather \(p\wedge \neg q\)). However, v is not ruled out as an alternative for p, for p is false at v and yet the agent believes p at v. This explains the consequence of Theorem 5.2 that \(K(p\wedge q)\rightarrow Kp\) is not valid in S-semantics, because one may safely believe p ∧ q at a world w even though one does not safely believe p at w. Note that the example also applies to sensitivity theories, for which we can again only say whether v is ruled out as an alternative for a given φ.
The distinction between the two notions of ruling out (RO) is again that of ∀∃ vs. ∃∀, as in the case of RS ∀∃ vs. RS ∃∀ in Section 3. Let us state the distinction in terms of possibilities that are not ruled out, possibilities that are uneliminated:
According to an RO ∀∃ theory, for every context 𝒞, world w, and (∀) proposition P, there is (∃) a set of worlds \(\mathsf {u}_{_{\mathcal {C}}}(P,w)\subseteq \overline {P}\) uneliminated at w as alternatives for P, such that if any world in \(\mathsf {u}_{_{\mathcal {C}}}(P,w)\) is relevant (i.e., in \(\mathsf {r}_{_{\mathcal {C}}}(P,w)\)), then the agent does not know P in w (relative to 𝒞).
According to an RO ∃∀ theory, for every context 𝒞 and world w, there is (∃) a set of worlds \(\mathsf {U}_{_{\mathcal {C}}}(w)\) uneliminated at w, such that for every (∀) proposition P, if any world in \(\mathsf {U}_{_{\mathcal {C}}}(w)\cap \overline {P}\) is relevant (i.e., in \(\mathsf {r}_{_{\mathcal {C}}}(P,w)\)), then the agent does not know P in w (relative to 𝒞).
Every RO ∃∀ theory is a RO ∀∃ theory (with \(\mathsf {u}_{_{\mathcal {C}}}(P,w)=\mathsf {U}_{_{\mathcal {C}}}(w)\cap \overline {P}\)), but when I refer to RO ∀∃ theories I have in mind those that are not RO ∃∀. As noted, L/D-semantics formalize RO ∃∀ theories, with ⇾(w) (Notation 5.12) in the role of U(w), while S/H/N-semantics formalize RO ∀∃ theories, given the role of belief in their notions of ruling out, noted above (see [38, Section 3.3.2]).
Consider the parallel between RO ∀∃ and RS ∀∃ parameter settings: given a ∀∃ setting of the RO (resp. RS) parameter, a (¬φ ∧ ¬ψ)-world that is ruled out as an alternative for φ (resp. that must be ruled out in order to know φ) may not be ruled out as an alternative for ψ (resp. may not be such that it must be ruled out in order to know ψ), because whether the world is ruled out or not (resp. relevant or not) depends on the proposition in question, as indicated by the ∀ propositions ∃ set of uneliminated (resp. relevant) worlds quantifier order. As the example of Fig. 10 shows, the RO ∀∃ setting for safety explains why closure fails in S-semantics, despite its RS ∃∀ setting.
Table 2 summarizes the relation between the two theory parameters and closure failures. Not all theories with RS ∀∃ or RO ∀∃ settings must have the same closure failures as described by Theorem 5.2. Elsewhere I show that as a result of their particular RO ∀∃ character, variants of subjunctivism, such as DeRose [17] modified tracking theory and the safety theory with bases, do not avoid serious closure failures [38, Sections 2.10.1, 2.D]. However, in part II we will see how a kind of generalized RS ∀∃ theory can avoid the worst of the subjunctivist-flavored theories, while still stopping short of full closure. This theory will solve the Dretskean closure dilemma raised at the end of Section 3.
10 Conclusion of Part I
In this paper, we have investigated an area where epistemology and epistemic logic naturally meet: the debate over epistemic closure, involving two of the most influential views in contemporary epistemology—relevant alternatives and subjunctivism. Our model-theoretic approach helped to illuminate the structural features of RA and subjunctivist theories that lead to closure failure, as well as the precise extent of their closure failures in Theorem 5.2.
When understood as theories of knowledge, the basic subjunctivist-flavored theories formalized by D/H/N/S-semantics have a bad balance of closure properties. Not only do they invalidate very plausible closure principles (recall Section 5), illustrating the problem of containment (recall Section 1), but also they validate some questionable ones (recall Section 7). The theories formalized by C- and L-semantics also have their problems. On the one hand, the idea that knowledge requires ruling out all possibilities of error, reflected in C-semantics, makes knowing too hard, giving us the problem of skepticism (recall Sections 2 and 3). On the other hand, the idea that knowledge of contingent empirical truths can be acquired with no requirement of eliminating possibilities, reflected in L-semantics (and S-semantics), seems to make knowing too easy, giving us the problem of vacuous knowledge (recall Sections 3 and 4). An attraction of D/H/N-semantics is that they avoid these problems. But they do so at a high cost when it comes to closure.
In Part II, I will propose a new picture of knowledge that avoids the problems of skepticism and vacuous knowledge, without the high-cost closure failures of the subjunctivist-flavored theories. As we shall see, the model-theoretic epistemic-logical approach followed here can help us not only to better understand epistemological problems, but also to discover possible solutions.
The results of this paper motivate some methodological reflections on our approach. In epistemology, a key method of theory assessment involves considering the verdicts issued by different theories about which knowledge claims are true in a particular scenario. This is akin to considering the verdicts issued by different semantics about which epistemic formulas are true in a particular model. All of the semantics we studied can issue different verdicts for the same model. Moreover, theorists who favor different theories/semantics may represent a scenario with different models in the first place. Despite these differences, there are systematic relations between the RA, tracking, and safety perspectives represented by our semantics. In several cases, we have seen that any model viewed from one perspective can be transformed into a model that has an equivalent epistemic description from a different perspective (Propositions 6.1–6.3). As we have also seen, when we rise to the level of truth in all models, of validity, differences may wash away, revealing unity on a higher level. Theorem 5.2 provided such a view, showing that four different epistemological pictures validate essentially the same epistemic closure principles. Against this background of similarity, subtle differences within the RA/subjunctivist family appear more clearly. The picture offered by total relevant alternatives models lead to a logic of ranked relevant alternatives, interestingly different from the others (Corollary 7.1). In the realm of higher-order knowledge, there emerged hierarchies in the strength of different theories (Corollary 8.12).
For some philosophers, a source of hesitation about epistemic logic is the degree of idealization. In basic systems of epistemic logic, agents know all the logical consequences of what they know, raising the “problem of logical omniscience” noted in Section 1. However, in our setting, logical omniscience is a feature, not a bug. Although in our formalizations of the RA and subjunctivist theories, agents do not know all the logical consequences of what they know, due to failures of epistemic closure, they are still logically omniscient in another sense. For as “ideally astute logicians” (recall Section 2), they know all logically valid principles, and they believe all the logical consequences of what they believe. These assumptions allow us to distinguish failures of epistemic closure that are due to fact that finite agents do not always “put two and two together” from failures of epistemic closure that are due to the special conditions on knowledge posited by the RA and subjunctivist theories.Footnote 63 This shows the positive role that idealization can play in epistemology, as it does in science.
Notes
Lawlor [47, 44] makes the methodological point about the advantage of raising the containment problem. It is noteworthy that Hawthorne takes a kind of proof-theoretic approach; he argues that a certain set of closure principles, not including K, suffices to derive the consequences that those who deny K wish to avoid, in which case they must give up a principle in the set. By contrast, our approach will be model-theoretic; we will study models of particular theories to identify those structural features that lead to closure failures.
While closure failures for these subjunctivist-flavored theories go too far in some directions, in other directions they do not go far enough for the purposes of Dretske and Nozick: all of these theories validate closure principles (see Section 5) that appear about as dangerous as K in arguments for radical skepticism about knowledge. This fact undermines the force of responding to skepticism by rejecting K on subjunctivist grounds, as Nozick does.
Perhaps it has never been documented, but it is a possibility of medical theory.
Local skeptics about medical knowledge may substitute one of the standard cases with a similar structure involving, e.g., disguised mules, trick lighting, etc. (see Dretske [19]).
For convenience, I use ‘c’, ‘c′’, and ‘x’ not only as names of medical conditions, but also as symbols for atomic sentences with the obvious intended meanings—that the patient has condition c, c′, and x, respectively. Also for convenience, I will not bother to add quotes when mentioning symbolic expressions.
This statement of the dilemma ignores the option of contextualism, investigated in Holliday [37, 38]. Stine [70], Lewis [52], and Cohen [13] propose contextualist versions of the RA theory, while DeRose [17] proposes a contextualist version of Nozick’s tracking theory. See DeRose [18] for a state of the art treatment of contextualism.
Note the distinction with a stronger property of consequence omniscience (standardly “logical omniscience”), that one knows all the logical consequences of what one knows.
We may add that such an agent has come to believe these logical consequences by “competent deduction,” rather than (only) by some other means, but we will not explicitly represent methods or bases of beliefs here (see Remark 2.3). By “all the logical consequences” I mean all of those involving concepts that the agent grasps. Otherwise one might believe p and yet fail to believe p ∨ q because one does not grasp q (see Williamson [78, 283]). Assume that the agent grasps all of the atomic p, q, r, … of Definition 2.2.
It is not difficult to extend the framework of Sections 3 and 4 to study closure principles of the form shown below where the φ’s and ψ’s may contain first-order quantifiers, provided that no free variables are allowed within the scope of any K operator. The closure behavior of K with respect to ∀ and ∃ can be anticipated from the closure behavior of K with respect to ∧ and ∨ shown in Theorem 5.2. Of course, interesting complications arise whenever we allow quantification into the scope of a K operator (see Holliday and Perry [41]).
Harman and Sherman [31] criticize Williamson’s [78] talk of “deduction” as extending knowledge for its “presupposition that deduction is a kind of inference, something one does” (495). Our talk of an agent coming to believe ψ by “competent deduction” from φ 1, …, φ n can be taken as elliptical for the following (cf. Harman [31, 496]): the agent constructs a valid deduction from believed premises φ 1, …, φ n to conclusion ψ, recognizes that the construction is a valid deduction, and comes to believe ψ on that basis.
Deductive closure principles belong to a more general category of “active” closure principles, which are conditional on the agent performing some action, of which deduction is one example. As Johan van Benthem (personal communication) suggests, the active analogue of K has the form Kφ ∧ K (φ ⇾ ψ) ⇾ [a]Kψ, where [a] stands for after action a.
There are problematic failures of pure and deductive closure for the tracking theory with methods, for the structural reasons identified here. The safety theory with bases may support deductive closure (although see Alspector-Kelly [3]), but it also has problems with pure closure for the structural reasons identified here. See Holliday [38, Section 2.D].
In order to deal with self-locating knowledge, one may take the alternatives to be “centered” worlds or possible individuals (see Lewis [51, Section 1.4] and references therein). Another question is whether we should think of what is ruled out by knowledge as including ways the world could not be (metaphysically “impossible worlds” or even logically impossible worlds), in addition to ways the world could be. See King [42] on this question and Chalmers [11] on ways the world might be vs. ways the world might have been.
If one were to also adopt a variant of Lewis’s [52] Rule of Belief according to which any world v doxastically accessible for the agent in w must be relevant and uneliminated for the agent in w (i.e., using notation introduced below, wDv implies \(v\in \text {Min}_{\preceq _{w}}(W)\) and w ⇾ v), then belief would already follow from the knowledge condition of Definition 3.4.
Lewis [52] is neutral on whether the possibilities referred to in his definition of knowledge must be “maximally specific” (552), as worlds are often thought to be. It should be clear that our examples do not depend on taking possibilities to be maximally specific either.
Those who have used standard Kripke models for epistemic modeling should note an important difference in how we use W and ⇾. We include in W not only possibilities that the agent has not eliminated, but also possibilities that the agent has eliminated, including possibilities v such that
 for all w distinct from v. While in standard Kripke semantics for the (single-agent) epistemic language, such a possibility v can always be deleted from W without changing the truth value of any formula at w (given the invariance of truth under ⇾-generated submodels), this will not be the case for one of our semantics below (D-semantics). So if we want to indicate that an agent in w has eliminated a possibility v, we do not leave it out of W; instead, we include it in W and set
for all w distinct from v. While in standard Kripke semantics for the (single-agent) epistemic language, such a possibility v can always be deleted from W without changing the truth value of any formula at w (given the invariance of truth under ⇾-generated submodels), this will not be the case for one of our semantics below (D-semantics). So if we want to indicate that an agent in w has eliminated a possibility v, we do not leave it out of W; instead, we include it in W and set  .
.One might expect u ≤ w v to mean that v is at least as relevant (at w) as u is, by analogy with x ≤ y in arithmetic, but Lewis’s [49, Section 2.3] convention is now standard.
In part II, I argue that there is a better way of understanding Dretske’s [21] RS ∀∃ theory, without the familiar world-ordering picture. Hence I take the ‘D’ for D-semantics as loosely as the ‘C’ for C-semantics. Nonetheless, it is a helpful mnemonic for remembering that D-semantics formalizes an RA theory that allows closure failure, as Dretske’s does, while L-semantics formalizes an RA theory that does not, like Lewis’s.
Instead of thinking in terms of three different satisfaction relations, ⊨ c , ⊨ d , and ⊨ l , some readers may prefer to think in terms of one satisfaction relation, ⊨, and three different operators, K c , K d , and K l . I choose to subscript the turnstile instead of the operator in order to avoid proliferating subscripts in formulas. One should not read anything more into this practical choice of notation. (However, note that epistemologists typically take themselves to be proposing different accounts of the conditions under which an agent has knowledge, rather than proposing different epistemic notions of knowledge1, knowledge2, etc.)
We ignore the relevance orderings for the other worlds. We also ignore which possibilities are ruled out at worlds other than w 1, since we are not concerned here with student A’s higher-order knowledge at w 1. If we were, then we might include other worlds in the model.
It is easy to see that for D-semantics (and H/N/S-semantics in Section 4), knowledge fails to be closed not only under known material implication, but even under known strict implication: \(K\varphi \wedge K\Box (\varphi \rightarrow \psi )\rightarrow K\psi \), with the □ in Definition 8.5 (or even the universal modality).
Heller [33] argues that the orderings for relevance and similarity are the same, only the boundary of the relevant worlds that one must rule out in order to know may extend beyond that of the most similar worlds. See the remarks in note 26 below.
Nozick used the term ‘variation’ for what I call ‘sensitivity’ and used ‘sensitivity’ to cover both variation and adherence; but the narrower use of ‘sensitivity’ is now standard.
Nozick [58, 680n8] tentatively proposes alternative truth conditions for counterfactuals. However, he also indicates that his theory may be understood in terms of Lewis’s semantics for counterfactuals (but see Observation 4.5). This has become the standard practice in the literature. For example, see Vogel [73], Comesaña [15], and Alspector-Kelly [3].
In Definition 4.3, I state the sensitivity, adherence, and safety conditions using the \(\text {Min}_{\leqslant _{w}}\) operator, which when applied to a set S of worlds gives the set of “closest” worlds to w out of those in S. This appears to conflict with the views of Heller [33, 34], who argues for a “close enough worlds” analysis rather than a “closest worlds” analysis for sensitivity, and of Pritchard [60, 72], who argues for considering nearby rather than only nearest worlds for safety and sensitivity. However, the conflict is merely apparent. For if one judges that the closest worlds in a set S, according to ≤ w , do not include all of the worlds in S that are close enough, then we can relax ≤ w to a coarser preorder \(\leqslant '_{w}\), so that the closest worlds in S according to \(\leqslant '_{w}\) are exactly those worlds in S previously judged to be closest or close enough. To be precise, given a set CloseEnough(w) ⊆ W w such that \(\text {Min}_{\leqslant _{w}}(W)\subseteq CloseEnough(w)\) y ∈ CloseEnough(w) and \(x\leqslant _{w} y\), then \(x\in CloseEnough(w)\), define \(\leqslant _{w}'\) as follows: \(v\leqslant _{w}'u\) iff either \(v\leqslant _{w}u\) or [\(u\leqslant _{w}v\) and \(v\in CloseEnough(w)\)]. Then \(\text {Min}_{\leqslant '_{w}}(S)=\text {Min}_{\leqslant _{w}}(S)\cup (CloseEnough(w)\cap S)\), so the close enough S-worlds are included, as desired. For the coarser preorder \(\leqslant '_{w}\), \(\text {Min}_{\leqslant '_{w}}(W)=CloseEnough(w)\) would be the set of worlds close enough/nearby to w. Here we assume, following Heller [34, 201f], that whether a world counts as close enough/nearby may be context dependent, but for a fixed context, whether a world is close enough/nearby is not relative to the φ for which we are assessing Kφ (cf. Cross [16] on counterfactual conditionals and antecedent-relative comparative world similarity); as discussed in Section 2, the fact that (for a given world) there is a single, fixed ordering on the set of worlds is what Heller [34] uses to reply to Stine’s [70] equivocation charge against Dretske. Finally, note that while the coarser preorder \(\leqslant _{w}'\) may not be the appropriate relation for assessing counterfactuals, according to the Heller/Pritchard view, it would be appropriate for assessing knowledge.
Suppose that C is a necessary but insufficient condition for knowledge, and let Cφ mean that the agent satisfies C with respect to φ. Hence Kφ → Cφ should be valid. Further suppose that (A) \(C\varphi _{1}\wedge \dots \wedge C\varphi _{n}\rightarrow C\psi \) is not valid. As Vogel [73], Warfield [77], and others point out, it does not follow that (B) \(K\varphi _{1}\wedge \dots \wedge K\varphi _{n}\rightarrow K\psi \) is not valid. For in the counterexample to (A), \(K\varphi _{1}\wedge \dots \wedge K\varphi _{n}\) may not hold, since C is not sufficient for K.
Let C′ be another insufficient condition such that C and C′ are jointly sufficient for K, so \(C\varphi \wedge C'\varphi \rightarrow K\varphi \) is valid. If (B) is valid, then \(C'\varphi _{1}\wedge \dots \wedge C'\varphi _{n}\) does not hold in the counterexample to (A). Moreover, it must be that while (A) is not valid, \(C\varphi _{1}\wedge \dots \wedge C\varphi _{n}\wedge C'\varphi _{1}\wedge \dots \wedge C'\varphi _{n}\rightarrow C\psi \) is valid. For if there is a counterexample to the latter, then there is a counterexample to (B), since C and C′ are jointly sufficient and C is necessary for K.
The problem is that proposed conditions for K are typically independent in such a way that assuming one also satisfies C′ with respect to \(\varphi _{1},\dots ,\varphi _{n}\) will not guarantee that one satisfies a distinct, non-redundant condition C with respect to ψ, if satisfying C with respect to \(\varphi _{1},\dots ,\varphi _{n}\) is not already sufficient. For example, if ruling out the relevant alternatives to \(\varphi _{1},\dots ,\varphi _{n}\) is not sufficient for ruling out the relevant alternatives to ψ, then what other condition is such that also satisfying it with respect to \(\varphi _{1},\dots ,\varphi _{n}\) will guarantee that one has ruled out the relevant alternatives to ψ? The same question arises for subjunctivist conditions. It is up to subjunctivists to say what they expect to block closure failures for knowledge, given closure failures for their necessary subjunctivist conditions on knowledge.
One way to do so is to build in the satisfaction of closure itself as another necessary condition. For example, Luper-Foy [53, 45n38] gives the “trivial example” of contracking φ, which is the condition (C′) of satisfying the sensitivity condition (C) for all logical consequences of φ. However, this idea for building in closure misses the fact that multi-premise closure principles fail for contracking. For example, one can contrack p and contract q, while being insensitive with respect to (p ∧ (q) ∨ (r and therefore failing to contrack p ∧ q.
Contracking must be distinguished from another idea for combining tracking with closure. Roush [62, 63, Ch. 2, Section 1] proposes a disjunctive account according to which (to a first approximation) an agent knows ψ iff either the agent “Nozick-knows” ψ, i.e., satisfies Nozick’s belief, sensitivity, and adherence conditions for ψ, or there are some \(\varphi _{1},\dots ,\varphi _{n}\) such that the agent knows \(\varphi _{1},\dots ,\varphi _{n}\) and knows that \(\varphi _{1}\wedge \dots \wedge \varphi _{n}\) implies ψ (cf. Luper-Foy [53, 46] on “distracking”). Importantly, according to this recursive tracking view of knowledge, the tracking conditions (for which closure fails) are not necessary conditions for knowledge.
It is not essential here that we model belief with a doxastic accessibility relation. When we show that a given closure principle is H/N/S-valid, we use the fact that the truth clause for Bφ in Definition 4.3 guarantees some doxastic closure (see Fact 5.11); but when we show that a closure principle is not H/N/S-valid, we do not use any facts about doxastic closure, as one can verify by inspection of the proofs. For the purpose of demonstrating closure failures, we could simply associate with each w ∈ W a set Σ w of formulas such that ℳ, w ⊨ Bφ iff φ ∈ Σ w . However, if we were to assume no doxastic closure properties for Σ w , then there would be no valid epistemic closure principles (except Kφ → Kφ), assuming knowledge requires belief. As a modeling choice, this may be more realistic, but it throws away information about the reasons for closure failures. For we would no longer be able to tell whether an epistemic closure principle such as Kφ → K(φ v ψ) is not valid for the (interesting) reason that the special conditions for knowledge posited by a theory are not preserved in the required way, or whether the principle is not valid for the (uninteresting) reason that there is some agent who knows φ but happened not to form a belief in φ ∨ ψ.
Alternatively, the sphere of worlds for adherence could be independent of the relation ≤ w for sensitivity, i.e., distinct from \(\text {Min}_{\leqslant _{w}}(W)\) (see Holliday [38, Remark 3.2]), so ≤ w could be centered without trivializing adherence. But this would allow cases in which an agent knows φ even though she believes φ in a ¬φ-world that is “close enough” to w to be in its adherence sphere (provided there is a closer ¬φ-world according to ≤ w in which she does not believe φ). Nozick [58, 680n8] suggests interpreting adherence counterfactuals φ □→ Bφ with true antecedents in such a way that the sphere over which φ → Bφ must hold may differ for different φ. By contrast, Observation 4.5 shows that we are interpreting adherence as a kind of ∃∀ condition, in a sense that generalizes that of Section 3 to cover a requirement that one meet an epistemic success condition in all P-worlds in R 𝒞 (w) (see Holliday [38, Section 3.3.2]). A ∀∃ interpretation of adherence that, e.g., allows the adherence sphere for φ ∨ ψ to go beyond that of φ, would create another source of closure failure (see Sections 5.5 and 9).
Note that safety and tracking theorists may draw different models, with different ≤ w relations and \(\text {Min}_{\leqslant _{w}}(W)\) sets, to represent the epistemic situation of the same agent.
What about w 4? In Section 3, we assumed that A learned from textbooks that x confers immunity to c, so she had eliminated w 4 at w 1. In Fig. 2, that the only arrow from w 4 goes to w 4 indicates that if (contrary to biological law) x did not confer immunity to c and the patient had both c and x, then A would believe that the patient had both c and x, perhaps because the textbooks and tests would be different in such a world. However, all we need to assume for the purposes of our example is that if the patient had both c and x, then it would be compatible with what A believes that the patient had both c and x, as indicated by the reflexive loop. We can have other outgoing arrows from w 4 as well.
Roughly, Nozick [58, 231ff] proposes than an agent knows ψ via inference from φ iff (1) \(K\varphi \), (2) she infers the true conclusion ψ from premise φ, (3) \(\neg \psi {\kern 2pt}\Box {\kern -0.6pt} \rightarrow \neg B\varphi \), and (4) \(\psi {\kern 2pt}\Box {\kern -0.6pt} \rightarrow B\varphi \). Whether this proposal is consistent with the rest of Nozick’s theory depends on whether (1)–(4) ensure that the agent tracks ψ, which is still necessary for her to know ψ (234); and that depends on what kind of modal connection between Bφ and Bψ is supposed to follow from (2), because (1), (3), and (4) together do not ensure that she tracks ψ.
While Nozick [58] admits that such a closure failure “surely carries things too far” (230n64, 692), he also says that an agent can know p and yet fail to know \(\neg (\neg p \wedge ~\text {SK})\) (228). But the latter is logically equivalent to \(p \vee \neg ~\text {SK}\), and Nozick accepts closure under (known) logical equivalence (229). Nozick suggests (236) that closure under deducing a disjunction from a disjunct should hold, provided methods of belief formation are taken into account. However, Holliday [38, Section 2.D] shows that taking methods into account does not help here.
Following standard convention, we take an empty disjunction to be ⊥, so a closure principle χ n,0 with no Kψ formulas is of the form \(\varphi _{0}\wedge K\varphi _{1}\wedge \dots \wedge K\varphi _{n}\rightarrow \bot \).
Following standard convention, if Φ = ∅, we take \(\underset {\varphi \in \Phi }{\bigwedge }\varphi \) to be ⊤.
When I refer to (d) from part 4, I mean the condition that \(\underset {\varphi \in \Phi }{\bigwedge }\varphi \leftrightarrow \psi \) is H/N/S-valid.
In the following argument, ‘relevant’ means relevant at w (i.e., according to ≤ w ) and ‘uneliminated’/‘eliminated’ means uneliminated/eliminated at w (i.e., w ⇾ v or
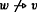 ).
).When dealing with both RA and CB models, I use ≤ w to stand for ≤ w or ≤ w .
For H-semantics without well-foundedness (but with totality), define a new \(\vDash _{h'}\) relation as in (5.16) but with \(\mathcal {M},u\nvDash _{h'}B\varphi \) in place of
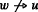 and with the belief condition for knowledge. Then the proof of the ‘if’ direction of Theorem 5.2.4 for \(\vDash _{h'}\) is similar to the proof above for \(\vDash _{d'}\), but replacing (c) by (d) and replacing
and with the belief condition for knowledge. Then the proof of the ‘if’ direction of Theorem 5.2.4 for \(\vDash _{h'}\) is similar to the proof above for \(\vDash _{d'}\), but replacing (c) by (d) and replacing  in (5.17) by \(\mathcal {M},u\nvDash _{h'}B\psi \), which follows from \(\mathcal {M},u\nvDash _{h'}B\varphi \) for any \(\varphi \in \Phi \) by (d) and Fact 5.11. Without totality, we use the truth clause for K from the previous footnote but with \(\mathcal {M},u\nvDash B\varphi \) in place of
in (5.17) by \(\mathcal {M},u\nvDash _{h'}B\psi \), which follows from \(\mathcal {M},u\nvDash _{h'}B\varphi \) for any \(\varphi \in \Phi \) by (d) and Fact 5.11. Without totality, we use the truth clause for K from the previous footnote but with \(\mathcal {M},u\nvDash B\varphi \) in place of  and with the belief condition (see Holliday [38, Section 2.6.1]). Finally, since Definition 3.1.3b implies that \(\text {Min}_{\leqslant _{w}}(W)\not =\emptyset \) even if ≤
w
is not well-founded, it follows from Observation 4.5 that the adherence and safety conditions of N/S-semantics do not require well-foundedness.
and with the belief condition (see Holliday [38, Section 2.6.1]). Finally, since Definition 3.1.3b implies that \(\text {Min}_{\leqslant _{w}}(W)\not =\emptyset \) even if ≤
w
is not well-founded, it follows from Observation 4.5 that the adherence and safety conditions of N/S-semantics do not require well-foundedness.Recall that \(\chi _{n,0}\) is of the form \(\varphi _{0}\wedge K\varphi _{1}\wedge \dots \wedge K\varphi _{n}\rightarrow \bot \).
If we want to stay within the class of linear models, then we must change the definition of \(\preceq _{w}^{\mathcal {N}}\) so that it extends the linear order ≤ w with an arbitrary linear order on \(W^{\star }\) that makes all worlds in \(W^{\star }\) less relevant than all worlds in W, and similarly for \(\preceq _{w^{\star }}^{\mathcal {N}}\).
Cf. Theorem 4.2 of Friedman and Halpern [24] for a proof that the complexity of satisfiability for formulas of conditional logic in similar preorder structures is in PSPACE.
The \(x_{t}\) and \(u_{j}^{k}\) worlds are not in the field of ≤ w . For a universal field (and total relation), the proof works with minor additions if we take the union of ≤ w as defined above with
$$\{\langle w,x_{t}\rangle,\langle w, u^{k}_{j}\rangle ,\langle v_{k},x_{t}\rangle, \langle v_{k},u^{k}_{j} \rangle, \langle x_{t},x_{t}\rangle, \langle x_{t},u^{k}_{j}\rangle,\langle u^{k}_{j},u^{k}_{j}\rangle \mid t\in T, k\in P_{m}\setminus T, j\in P_{n}\setminus S_{k}\}.$$In fact, we only need something weaker, namely, that it would be compatible with what the agent believes that the true situation is v, i.e., v D v. In the
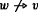 case of the definition of D in the proof of Proposition 6.1, we only need that \(v\in D(v)\) for the proof to work.
case of the definition of D in the proof of Proposition 6.1, we only need that \(v\in D(v)\) for the proof to work.It is easy to see that even if we forbid centered models, Proposition 6.2 will still hold. For we can allow any number of worlds in \(\text {Min}_{\leqslant _{w}'}(W)\), provided they do not witness a violation of the adherence condition at w for any φ for which we want \(\mathcal {N},w\vDash _{n} K\varphi \).
It is easy to see that even if we require \(W_{w}\setminus ~\text {Min}_{\leqslant _{w}'}(W)\not =\emptyset \), Proposition 6.2 will still hold. For we can allow any number of worlds in \(W_{w}\setminus ~\text {Min}_{\leqslant _{w}'}(W)\), provided they do not witness a violation of the sensitivity condition at w for any φ for which we want \(\mathcal {N},w\vDash _{h} K\varphi \).
Corollary 7.1.4 gives an answer, for the flat fragment, to the question posed by van Benthem [8, 153] of what is the epistemic logic of Nozick’s notion of knowledge.
The usual canonical model approach used for K and other normal modal logics seems more difficult to apply to RA and CB models, since we must use maximally consistent sets of formulas in the epistemic language only (cf. note 61) to guide the construction of both the orderings ≤ w (resp. ≤ w ) and relation ⇾ (resp. D), which must be appropriately related to one another for the truth lemma to hold. In this situation, our alternative approach performs well.
If \(n=0\), we can take the left side of the premise/conclusion of RAT to be \(\top \), or we can simply take the premise to be \(\psi _{1}\wedge \dots \wedge \psi _{m}\) and the conclusion to be \(K\psi _{1}\vee \dots \vee K\psi _{m}\).
Here I mean either the problem of checking provability/validity or that of checking consistency/satisfiability, given that PSPACE is closed under complementation. When I refer to NP-completeness, I have in mind the consistency/satisfiability problem.
In fact, Allen [2] shows that adding any degree of conjunctive closure, however weak, to the classical modal logic EMN results in a jump from NP- to PSPACE-completeness. Adding the full strength of C is sufficient, but not necessary. As far as I know, lower bounds for the complexity of systems with C but without M have not yet been established.
Whether such complexity facts have any philosophical significance seems to be an open question. As a cautionary example, one would not want to argue that it counts in favor of the plausibility of the 5 axiom, \(\neg K\varphi \rightarrow K\neg K\varphi \), that while the complexity of K is PSPACE-complete, for any extension of K5, complexity drops to NP-complete [30]. That being said, if we are forced to give up C for epistemological reasons, then its computational costliness in reasoning about knowledge may make us miss it less.
It follows from Lewis’s [52, 556f] Rule of Resemblance that if some ¬p-possibility w 2 “saliently resembles” w 1, which is relevant at w 1 by the Rule of Actuality, then w 2 is relevant at w 1, so you must rule out w 2 in order to know p in w 1. Lewis is explicit (555) that by ‘actuality’ he means the actuality of the subject of knowledge attribution. Hence if we consider your counterpart in some w 3, and some ¬p-possibility w 4 saliently resembles w 3, then your counterpart must rule out w 4 in order to know p in w 3. However, if salient resemblance is possibility-relative, as comparative similarity is for Lewis, then w 4 may not saliently resemble w 1, in which case you may not need to rule out w 4 in order to know p in w 1. (By Lewis’s Rule of Attention (559), our attending to w 4 in this way may shift the context 𝒞 to a context 𝒞′ in which w 4 is relevant, but the foregoing points still apply to 𝒞.) This is all that is required for Example 8.1 to be consistent with Lewis’s theory.
One difference between Fact 8.7 and Fact 8.9 is that the former applies to any theory for which sensitivity is a necessary condition for knowledge, whereas the latter could in principle be blocked by theories that propose other necessary conditions for knowledge in addition to sensitivity or safety. What Fact 8.9 shows is that sensitivity and safety theorists have some explaining to do about what they expect to block such a counterintuitive result.
Rewrite \(\neg K(p\wedge \neg Kp)\) as \(K(p\wedge \neg Kp)\rightarrow \bot \). T-unpacking gives \(p\wedge \neg Kp\wedge K(p\wedge \neg Kp)\rightarrow \bot \) and then \(p \wedge K(p\wedge \neg Kp)\rightarrow Kp\), which fails (a), (c), and (d) of Theorem 5.2.
One can of course add more worlds to \(W_{w_{2}}\) than are shown in Fig. 9.
If we require more properties of the D relation, then more principles will be valid in H/N/S-semantics—obviously for the B operator, but also for the interaction between K and B. For example, if require that D be dense, so BBφ → Bφ is valid, then BBφ → KBφ is H/S-valid. If we also require that D be transitive, so Bφ → BBφ is valid, then Bφ → KBφ is H/N/S-valid. As Kripke [44, 183] in effect observes, if Bφ ↔ BBφ is valid, then (for propositional φ) \(\mathcal {M},w\vDash _{h} K\varphi \) implies \(\mathcal {M},w\vDash _{n} K(\varphi \wedge B\varphi )\), so whenever \(\mathcal {M},w\vDash _{h} K\varphi \) but \(\mathcal {M},w\nvDash _{n} K\varphi \) (because adherence is not satisfied), \(K(\varphi \wedge B\varphi )\rightarrow K\varphi \) fails according to N-semantics, an extreme closure failure.
If we extend the language of Definition 2.2 so that we can describe different parts of our CB models independently, e.g., by adding the belief operator B for the doxastic relation D or a counterfactual conditional □→ for the similarity relations ≤ w , then the problem of axiomatization becomes easier. For S-semantics, which does not use the structure of any ≤ w relation beyond \(\text {Min}_{\leqslant _{w}}(W)\), just adding B to the language makes the axiomatization problem easy. As one can prove by a standard canonical model construction, for completeness it suffices to combine the logic KD for B with the axiom Kφ → Bφ and the rule
$$\mathrm{SA.} ~\frac{(B\varphi_{1}\rightarrow\varphi_{1})\wedge\dots\wedge (B\varphi_{n}\rightarrow\varphi_{n}) \rightarrow(B\psi\rightarrow \psi)}{K\varphi_{1}\wedge\dots\wedge K\varphi_{n}\rightarrow (B\psi\rightarrow K\psi)} \,_{(n\geq 0)}. $$For H/N-semantics, adding not only B but also a counterfactual □→ (with the Lewisian semantics outlined in Section 4) makes the axiomatization problem easy. For example, for N-semantics we can combine KD for B with a complete system for counterfactuals (no interaction axioms between B and □→ are needed), plus Kφ → Bφ and Kφ ↔ Bφ ∧ (¬φ □→ ¬Bφ) ∧ (Bφ □→ φ). The problem with obtaining easy axiomatizations by extending the language in this way is that the resulting systems give us little additional insight. The interesting properties of knowledge are hidden in the axioms that combine several operators, each with different properties. Although in a complete system for the extended language we can of course derive all principles that could appear in any sound system for a restricted language, this fact does not tell us what those principle are or which set of them is complete with respect to the restricted language. Corollary 7.1 and Facts 8.7, 8.8, and 8.10 suggest that more illuminating principles may appear as axioms if we axiomatize the S-theory of CB models in the epistemic language or the H/N-theory of CB models in the epistemic-doxastic(-alethic) language.
Recall note 28. Williamson [81, 256] makes a similar point, namely that it can be useful to assume logical omniscience in order to discern the specific epistemic effects of limited powers of perceptual discrimination, as opposed to limited logical powers.
References
Adams, F., Barker, J. A., Figurelli, J. (2012). Towards closure on closure. Synthese, 188(2), 179–196.
Allen, M. (2005). Complexity results for logics of local reasoning and inconsistent belief. In R. van der Meyden (Ed.), Proceedings of the tenth conference on theoretical aspects of rationality and knowledge (TARK X) (pp. 92–108). National University of Singapore.
Alspector-Kelly, M. (2011). Why safety doesn’t save closure. Synthese, 183(2), 127–142.
Audi, R. (1988). Belief, justification, and knowledge. Belmont: Wadsworth Publishing.
Austin, J. (1946). Other minds. Proceedings of the Aristotelian Society, 20, 148–187.
Becker, K. (2006). Is counterfactual reliabilism compatible with higher-level knowledge? Dialectica, 60(1), 79–84.
Becker, K. (2007). Epistemology modalized. New York: Routledge.
van Benthem, J. (2010). Modal logic for open minds. Stanford: CSLI Publications.
Black, T. (2010). Modal and anti-luck epistemology. In S. Bernecker & D. Pritchard (Eds.), The routledge companion to epistemology (pp. 187–198). New York: Routledge.
Brueckner, A. (2004). Strategies for refuting closure for knowledge. Analysis, 64(4), 333–335.
Chalmers, D. J. (2011). The nature of epistemic space. In A. Egan & B. Weatherson (Eds.), Modality, epistemic (pp. 60–107). New York: Oxford University Press.
Chellas, B. F. (1980). Modal logic: an introduction. New York: Cambridge University Press.
Cohen, S. (1988). How to be a fallibilist. Philosophical Perspectives, 2, 91–123.
Cohen, S. (2002). Basic knowledge and the problem of easy knowledge. Philosophy and Phenomenological Research, 65(2), 309–329.
Comesaña, J. (2007). Knowledge and subjunctive conditionals. Philosophy Compass, 2(6), 781–791.
Cross, C. B. (2008). Antecedent-relative comparative world similarity. Journal of Philosophical Logic, 37(2), 101–120.
DeRose, K. (1995). Solving the skeptical problem. The Philosophical Review, 104(1), 1–52.
DeRose, K. (2009). The case for contextualism: knowledge, skepticism and context. New York: Oxford University Press.
Dretske, F. (1970). Epistemic operators. The Journal of Philosophy, 67(24), 1007–1023.
Dretske, F. (1971). Conclusive reasons. Australasian Journal of Philosophy, 49(1), 1–22.
Dretske, F. (1981). The pragmatic dimension of knowledge. Philosophical Studies, 40(3), 363–378.
Dretske, F. (2005). The case against closure. In M. Steup & E. Sosa (Eds.), Contemporary debates in epistemology (pp. 13–26). Malden: Blackwell Publishing.
Fitch, F. B. (1963). A logical analysis of some value concepts. The Journal of Symbolic Logic, 28(2), 135–142.
Friedman, N., & Halpern, J. Y. (1994). On the complexity of conditional logics. In J. Doyle, E. Sandwell, P. Torasso (Eds.), Proceedings of the fourth international conference on principles of knowledge representation and reasoning (KR’94) (pp. 202–213). San Francisco: Morgan Kaufman.
Goldman, A. H. (1975). A note on the conjunctivity of knowledge. Analysis, 36(1), 5–9.
Goldman, A. I. (1976). Discrimination and perceptual knowledge. The Journal of Philosophy, 73(20), 771–791.
Goldman, A. I. (1986). Epistemology and cognition. Cambridge: Harvard University Press.
Halpern, J. Y. (1995). The effect of bounding the number of primitive propositions and the depth of nesting on the complexity of modal logic. Artificial Intelligence, 75(2), 361–372.
Halpern, J. Y., & Pucella, R. (2011). Dealing with logical omniscience: expressiveness and pragmatics. Artificial Intelligence, 175(1), 220–235.
Halpern, J. Y., & Rêgo, L. C. (2007). Characterizing the NP-PSPACE gap in the satisfiability problem for modal logic. Journal of Logic and Computation, 17(4), 795–806.
Harman, G., & Sherman, B. (2004). Knowledge, assumptions, lotteries. Philosophical Issues, 14(1), 492–500.
Hawthorne, J. (2004). Knowledge and lotteries. New York: Oxford University Press.
Heller, M. (1989). Relevant alternatives. Philosophical Studies, 55(1), 23–40.
Heller, M. (1999a). Relevant alternatives and closure. Australasian Journal of Philosophy, 77(2), 196–208.
Heller, M. (1999b). The proper role for contextualism in an anti-luck epistemology. Noûs, 33(s13), 115–129.
Hintikka, J. (1962). Knowledge and belief: an introduction to the logic of the two notions. Ithaca:Cornell University Press.
Holliday, W.H. (2012a). Epistemic logic, relevant alternatives, and the dynamics of context. In D. Lassiter & M. Slavkovik (Eds.), New directions in logic, language and computation, lecture notes in computer science (Vol. 7415, pp. 109–129).
Holliday, W.H. (2012b). Knowing what follows: epistemic closure and epistemic logic. PhD thesis, Stanford University, revised version, ILLC dissertation series DS-2012-09.
Holliday, W.H. (2013a). Epistemic logic and epistemology. In S.O. Hansson & V.F. Hendricks (Eds.), Handbook of formal philosophy. Dordrecht: Springer, forthcoming.
Holliday, W.H. (2013b). Fallibilism and multiple paths to knowledge. In T.S. Gendler & J. Hawthorne, W.H. Holliday (Eds.), Oxford studies in epistemology (Vol. 5). New York: Oxford University Press, forthcoming.
Holliday, W.H., & Perry, J. (2013c). Roles, rigidity, and quantification in epistemic logic. In A. Baltag & S. Smets (Eds.), Johan F. A. K. van Benthem on logical and informational dynamics. Dordrecht: Springer, forthcoming .
King, J. C. (2007). What in the world are ways things might have been? Philosophical Studies, 133(3), 443–453.
Kripke, S. (1963). Semantical considerations on modal logic. Acta Philosophica Fennica, 16, 83–94.
Kripke, S. (2011). Nozick on knowledge. In Philosophical troubles: collected papers (Vol. 1, pp. 162–224). New York: Oxford University Press.
Kvanvig, J. L. (2006). Closure principles. Philosophy Compass, 1(3), 256–267.
Kyburg, H.E. Jr. (1961). Probability and the logic of rational belief . Middletown: Wesleyan University Press.
Lawlor, K. (2005). Living without closure. Grazer Philosophische Studien, 69, 25–49.
Lewis, D. (1971). Completeness and decidability of three logics of counterfactual conditionals. Theoria, 37(1), 74–85.
Lewis, D. (1973). Counterfactuals. Oxford: Basil Blackwell.
Lewis, D. (1981). Ordering semantics and premise semantics for counterfactuals. Journal of Philosophical Logic, 10(2), 217–234.
Lewis, D. (1986). On the plurality of worlds. Oxford: Basil Blackwell.
Lewis, D. (1996). Elusive knowledge. Australasian Journal of Philosophy, 74(4), 549–567.
Luper-Foy, S. (1984). The epistemic predicament: knowledge, Nozickian tracking, and scepticism. Australasian Journal of Philosophy, 62(1), 26–49.
Makinson, D. (1965). The paradox of the preface. Analysis, 25(6), 205–207.
McGinn, C. (1984). The concept of knowledge. Midwest Studies in Philosophy, 9(1), 529–554.
Murphy, P. (2005). Closure failures for safety. Philosophia, 33, 331–334.
Murphy, P. (2006). A strategy for assessing closure. Erkenntnis, 65(3), 365–383.
Nozick, R. (1981). Philosophical explanations. Cambridge: Harvard University Press.
Papadimitriou, C. H. (1994). Computational complexity. Reading: Addison-Wesley.
Pritchard, D. (2005). Epistemic luck. New York: Oxford University Press.
Pritchard, D. (2008). Sensitivity, safety, and antiluck epistemology. In J. Greco (Ed.), The Oxford handbook of skepticism (pp. 437–455). New York: Oxford University.
Roush, S. (2005). Tracking truth: knowledge, evidence and science. New York: Oxford University Press.
Roush, S. (2012). Sensitivity and closure. In K. Becker & T. Black (Eds.), The sensitivity principle in epistemology (pp. 242–268). New York: Cambridge University Press.
Rysiew, P. (2006). Motivating the relevant alternatives approach. Canadian Journal of Philosophy, 36(2), 259–279.
Sherman, B., & Harman, G. (2011). Knowledge and assumptions. Philosophical Studies, 156(1), 131–140.
Sosa, E. (1996). Postscript to proper functionalism and virtue epistemology. In J. Kvanvig (Ed.), Warrant in contemporary epistemology (pp. 271–281). Totowa: Rowman and Littlefield.
Sosa, E. (1999). How to defeat opposition to Moore. Noûs, 33(13), 141–153.
Stalnaker, R. (1968). A theory of conditionals. In N. Rescher (Ed.), Studies in logical theory (Vol. 2, pp. 98–112). Oxford: Basil Blackwell.
Stalnaker, R. (1991). The problem of logical omniscience, I. Synthese, 89(3), 425–440.
Stine, G. (1976). Skepticism, relevant alternatives, and deductive closure. Philosophical Studies, 29(4), 249–261.
Stroud, B. (1984). The significance of philosophical scepticism. New York: Oxford University Press.
Vardi, M. Y. (1989). On the complexity of epistemic reasoning. In Proceedings of the 4th IEEE symposium on logic in computer science (pp. 43–252).
Vogel, J. (1987). Tracking, closure, and inductive knowledge. In S. Luper-Foy (Ed.), The possibility of knowledge: nozick and his critics (pp. 197–215). Totowa: Rowman and Littlefield.
Vogel, J. (1999). The new relevant alternatives theory. Noûs, 33(s13), 155–180.
Vogel, J. (2000). Reliabilism leveled. The Journal of Philosophy, 97(11), 602–623.
Vogel, J. (2007). Subjunctivitis. Philosophical Studies, 134(1), 73–88.
Warfield, T. A. (2004). When epistemic closure does and does not fail: a lesson from the history of epistemology. Analysis, 64(1), 35–41.
Williamson, T. (2000). Knowledge and its limits. New York: Oxford University Press.
Williamson, T. (2001). Comments on Michael Williams’ contextualism, externalism, and epistemic standards. Philosophical Studies, 103(1), 25–33.
Williamson, T. (2009). Probability and danger. The Amherst Lecture in Philosophy, 4, 1–35. http://www.amherstlecture.org/williamson2009/.
Williamson, T. (2010). Interview. In V. Hendricks & O. Roy (Eds.), Epistemic logic: 5 questions (pp. 249–261). New York: Automatic.
Acknowledgments
I wish to thank everyone who provided helpful feedback on earlier versions of this paper, especially Johan van Benthem and Krista Lawlor, as well as Davide Grossi, Peter Hawke, Tomohiro Hoshi, Thomas Icard, Alistair Isaac, Neil Van Leeuwen, Helen Longino, Eric Pacuit, Sherrilyn Roush, and an anonymous referee for JPL.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Holliday, W.H. Epistemic Closure and Epistemic Logic I: Relevant Alternatives and Subjunctivism. J Philos Logic 44, 1–62 (2015). https://doi.org/10.1007/s10992-013-9306-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-013-9306-2


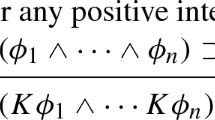












 for all w distinct from v. While in standard Kripke semantics for the (single-agent) epistemic language, such a possibility v can always be deleted from W without changing the truth value of any formula at w (given the invariance of truth under ⇾-generated submodels), this will not be the case for one of our semantics below (D-semantics). So if we want to indicate that an agent in w has eliminated a possibility v, we do not leave it out of W; instead, we include it in W and set
for all w distinct from v. While in standard Kripke semantics for the (single-agent) epistemic language, such a possibility v can always be deleted from W without changing the truth value of any formula at w (given the invariance of truth under ⇾-generated submodels), this will not be the case for one of our semantics below (D-semantics). So if we want to indicate that an agent in w has eliminated a possibility v, we do not leave it out of W; instead, we include it in W and set  .
.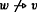 ).
).
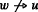 and with the belief condition for knowledge. Then the proof of the ‘if’ direction of Theorem 5.2.4 for
and with the belief condition for knowledge. Then the proof of the ‘if’ direction of Theorem 5.2.4 for  in (
in ( and with the belief condition (see Holliday [
and with the belief condition (see Holliday [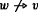 case of the definition of D in the proof of Proposition 6.1, we only need that
case of the definition of D in the proof of Proposition 6.1, we only need that