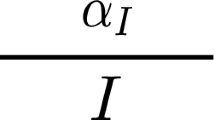Abstract
In this short note, we prove the following result: If a completely multiplicative function f : ℕ → [−1, 1] is small on average in the sense that ∑n ≤ xf(n) ≪ x1 − δ for some δ > 0, and if the Dirichlet series of f, say F(s), is such that F(1) = 0, then for any ϵ > 0, ∑p ≤ x(1 + f(p)) log p ≪ x1 − δ + ϵ. Moreover, a necessary condition for the existence of such f is that the Riemann zeta function ζ(s) has no zeros in the half-plane Re(s) > 1 − δ.
Similar content being viewed by others
References
M. Aymone and V. Sidoravicius, Partial sums of biased random multiplicative functions, J. Number Theory, 172:343–382, 2017, https://doi.org/10.1016/j.jnt.2016.08.020.
A. Granville and K. Soundararajan, Pretentious multiplicative functions and an inequality for the zeta-function, in Anatomy of Integers, CRM Proc. Lect. Notes, Vol. 46, AMS, Providence, RI, 2008, pp. 191–197.
D. Koukoulopoulos, On multiplicative functions which are small on average, Geom. Funct. Anal., 23(5):1569–1630, 2013, https://doi.org/10.1007/s00039-013-0235-6.
H.L. Montgomery and R.C. Vaughan, Multiplicative Number Theory. I: Classical Theory, Camb. Stud. Adv. Math., Vol. 97, Cambridge Univ. Press, Cambridge, 2007.
A.N. Shiryaev, Probability, 2nd ed., Grad. Texts Math., Vol. 95, Springer, New York, 1996, https://doi.org/10.1007/978-1-4757-2539-1. Translated from the first (1980) Russian edition by R.P. Boas.
G. Tenenbaum, Introduction to Analytic and Probabilistic Number Theory, Camb. Stud. Adv. Math., Vol. 46, Cambridge Univ. Press, Cambridge, 1995. Translated from the second (1995) French edition by C.B. Thomas.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Aymone, M. On multiplicative functions that are small on average and zero-free regions for the Riemann zeta function. Lith Math J 62, 146–149 (2022). https://doi.org/10.1007/s10986-022-09555-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10986-022-09555-y