Two-sample tests for survival data from observational studies

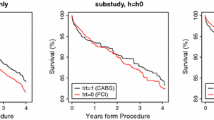
Abstract

When observational data are used to compare treatment-specific survivals, regular two-sample tests, such as the log-rank test, need to be adjusted for the imbalance between treatments with respect to baseline covariate distributions. Besides, the standard assumption that survival time and censoring time are conditionally independent given the treatment, required for the regular two-sample tests, may not be realistic in observational studies. Moreover, treatment-specific hazards are often non-proportional, resulting in small power for the log-rank test. In this paper, we propose a set of adjusted weighted log-rank tests and their supremum versions by inverse probability of treatment and censoring weighting to compare treatment-specific survivals based on data from observational studies. These tests are proven to be asymptotically correct. Simulation studies show that with realistic sample sizes and censoring rates, the proposed tests have the desired Type I error probabilities and are more powerful than the adjusted log-rank test when the treatment-specific hazards differ in non-proportional ways. A real data example illustrates the practical utility of the new methods.

Appendices

Appendix A

1.1 A.1. Notations and regularity conditions

We introduce the following notations that will be used in the regularity conditions below and the proof of Theorem 2:

$$\begin{aligned} V_Z({\varvec{\alpha }})= & {} E\left[ \frac{\exp ({\varvec{\alpha }}^T\tilde{{\mathbf {X}}}^Z)\tilde{{\mathbf {X}}}^{Z\otimes 2}}{\{1+\exp ({\varvec{\alpha }}^T\tilde{{\mathbf {X}}}^Z)\}}\right] ,\\ R_{Cj}^{(d)}(t;{\varvec{\theta }}_j)= & {} n^{-1}\sum _{i=1}^nY_{ij}(t){\mathbf {X}}_i^{C\otimes d}\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_i^C\right) ,\\ r_{Cj}^{(d)}(t;{\varvec{\theta }}_j)= & {} E\left\{ Y_{ij}(t){\mathbf {X}}_i^{C\otimes d}\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_i^C\right) \right\} ,\\ \bar{{\mathbf {X}}}_j^C(t;{\varvec{\theta }}_j)= & {} \frac{R_{Cj}^{(1)}(t;{\varvec{\theta }}_j)}{R_{Cj}^{(0)}(t;{\varvec{\theta }}_j)},\\ \bar{{\mathbf {x}}}_j^C(t;{\varvec{\theta }}_j)= & {} \frac{r_{Cj}^{(1)}(t;{\varvec{\theta }}_j)}{r_{Cj}^{(0)}(t;{\varvec{\theta }}_j)},\\ \varOmega _{j}^C({\varvec{\theta }}_j)= & {} \int _0^\infty \left\{ \frac{r_{Cj}^{(2)}(t;{\varvec{\theta }}_j)}{r_{Cj}^{(0)}(t;{\varvec{\theta }}_j)}-\bar{{\mathbf {x}}}_j^C(t;{\varvec{\theta }}_j)^{\otimes 2}\right\} E\{Y_{ij}(t)\lambda _{ij}^C(t)\}dt , \end{aligned}$$

and $S_{0j}^C(t)$ denotes the conditional survival function of C given $Z=j$ and ${\mathbf {X}}^C={\mathbf {0}}$ for $j=0,1$ and $d=0,1,2$, where for a column vector ${\mathbf {b}}$, ${\mathbf {b}}^{\otimes 2}={\mathbf {b}}{\mathbf {b}}^T$, ${\mathbf {b}}^{\otimes 1}={\mathbf {b}}$, and ${\mathbf {b}}^{\otimes 0}=1$. The rest notations appearing in Theorems 1 and 2 will be introduced as we prove Theorem 2.

We assume the following regularity conditions for $i=1,\ldots ,n$ and $j=0,1$:

• (a) Model (2) for treatment assignment is correctly specified.

• (b) Model (4) for censoring is correctly specified.

• (c) ${\mathbf {X}}_i^Z$ is bounded almost surely.

• (d) $V_Z({\varvec{\alpha }})$ is positive definite at the true value of ${\varvec{\alpha }}$.

• (e) ${\mathbf {X}}_i^C$ is bounded almost surely.

• (f) $\varOmega _j^C({\varvec{\theta }}_j)$ is positive definite at the true value of ${\varvec{\theta }}_j$.

• (g) $S_{(j)}(t)$ is absolutely continuous in t.

• (h) $S_{0j}^C(t)$ is absolutely continuous in t.

• (i) As $n\rightarrow \infty$, $W(s)\xrightarrow {p}w(s)$ uniformly on $\mathcal {I}$, where w(s) is a nonnegative, left-continuous function with right-hand limits on $\mathcal {I}$ such that $w(s)<\infty$ and its right-continuous adaptation $w^+$ has bounded variation on each closed subinterval of $\mathcal {I}$.

Conditions (a), (c) and (d) ensure the consistency and asymptotic normality of $\hat{{\varvec{\alpha }}}$. Conditions (b), (e) and (f) ensure the uniform consistency of $\hat{\varLambda }_{ij}^C(\cdot )$ over $[0,t_{\sup }]$ and the weak convergence of $\sqrt{n}\{\hat{\varLambda }_{ij}^C(\cdot )-\varLambda _{ij}^C(\cdot )\}$ to a zero-mean Gaussian process on $D[0,t_{\sup }]$. Conditions (g) and (h) ensure that $\exp \{-\hat{\varLambda }_{(j)}(\cdot )\}$ and $\exp \{-\hat{\varLambda }_{ij}^C(\cdot )\}$ are consistent estimators for $S_{(j)}(\cdot )$ and $S_{ij}^C(\cdot )$ respectively given the consistency of $\hat{\varLambda }_{(j)}(\cdot )$ and $\hat{\varLambda }_{ij}^C(\cdot )$. Condition (i) is needed for weak convergence of $W_a(t;\hat{{\varvec{\alpha }}},\hat{{\varvec{\varLambda }}}^C)$ to a zero-mean Gaussian process on $D[0,t_{\sup }]$ under $H_0$.

1.2 A.2. Proof of Theorem 2

We first decompose $W_a(t;\hat{{\varvec{\alpha }}},\hat{{\varvec{\varLambda }}}^C)$ as follows.

$$\begin{aligned} W_a(t;\hat{{\varvec{\alpha }}},\hat{{\varvec{\varLambda }}}^C)= & {} W_a(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)+\left\{ W_a(t;\hat{{\varvec{\alpha }}},\hat{{\varvec{\varLambda }}}^C)-W_a(t;{\varvec{\alpha }},\hat{{\varvec{\varLambda }}}^C)\right\} \nonumber \\&+\left\{ W_a(t;{\varvec{\alpha }},\hat{{\varvec{\varLambda }}}^C)-W_a(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\right\} . \end{aligned}$$

(16)

By algebra, $W_a(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)$ can be written as

$$\begin{aligned}&W_a(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\nonumber \\&\quad =\sum _{i=1}^n\int _0^t\frac{K^*(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{\sum _{k=1}^n\left[ p_{k1}({\varvec{\alpha }})\exp \left\{ -\varLambda _{k1}^C(s-)\right\} \right] ^{-1}Y_{k1}(s)}dM_{i1}^*(s)\nonumber \\&\qquad -\sum _{i=1}^n\int _0^t\frac{K^*(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{\sum _{k=1}^n\left[ p_{k0}({\varvec{\alpha }})\exp \left\{ -\varLambda _{k0}^C(s-)\right\} \right] ^{-1}Y_{k0}(s)}dM_{i0}^*(s)\nonumber \\&\qquad +\int _0^tK^*(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\{\lambda _{(1)}(s)-\lambda _{(0)}(s)\}ds \end{aligned}$$

(17)

Define $D_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\equiv E\left[ [p_{ij}({\varvec{\alpha }})\exp \{-\varLambda _{ij}^C(s-)\}]^{-1}Y_{ij}(s)\right]$ $(j=0,1)$ and $D(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\equiv \sum _{j=0}^1 D_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)$. Applying the Law of Large Number, then using conditions (a), (b), (h) and (i), when $n\rightarrow \infty$, we can re-express $W_a(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)$ as

$$\begin{aligned} W_a(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} n^{-1/2}\sum _{i=1}^n\left\{ A_{i1}(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)-A_{i0}(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\right\} \nonumber \\&+\int _0^tK^*(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\{\lambda _{(1)}(s)-\lambda _{(0)}(s)\}ds+o_p(1) \end{aligned}$$

(18)

with $E\{A_{ij}(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\}=0$ $j=(0,1)$.

To obtain the asymptotic expressions of the second and third summands in (16), we first derive the asymptotic expressions of $\sqrt{n}(\hat{{\varvec{\alpha }}}-{\varvec{\alpha }})$ and $\sqrt{n}\{\hat{\varLambda }_{ij}^C(t)-\varLambda _{ij}^C(t)\}$.

Under conditions (a), (c) and (d), we have from standard maximum likelihood theory $\hat{{\varvec{\alpha }}}\xrightarrow {p}{\varvec{\alpha }}$ and

$$\begin{aligned} \sqrt{n}(\hat{{\varvec{\alpha }}}-{\varvec{\alpha }})=V_Z^{-1}({\varvec{\alpha }})n^{-1/2}\sum _{i=1}^n{\varvec{\psi }}_i^Z({\varvec{\alpha }})+o_p(1), \end{aligned}$$

(19)

where ${\varvec{\psi }}_i^Z({\varvec{\alpha }})=\tilde{{\mathbf {X}}}_i^Z\{Z_i- expit ({\varvec{\alpha }}^T\tilde{{\mathbf {X}}}_i^Z)\}$.

Under conditions (b), (e) and (f), standard partial likelihood theory Fleming and Harrington (1991) leads to $\hat{{\varvec{\theta }}}_j\xrightarrow {p}{\varvec{\theta }}_j$,

$$\begin{aligned} \sqrt{n}(\hat{{\varvec{\theta }}}_j-{\varvec{\theta }}_j)=\left\{ \varOmega _j^C({\varvec{\theta }}_j)\right\} ^{-1}n^{-1/2}\sum _{i=1}^nU_{ij}^C({\varvec{\theta }}_j)+o_p(1), \end{aligned}$$

(20)

where $U_{ij}^C({\varvec{\theta }}_j)=\int _0^\infty \{{\mathbf {X}}_i^C-\bar{{\mathbf {x}}}_j^C(t;{\varvec{\theta }}_j)\}dM_{ij}^C(t)$, and

$$\begin{aligned} \sup _{t\in [0,t_{\sup }]}\left| \hat{\varLambda }_{0j}^C(t)-\varLambda _{0j}^C(t)\right| \xrightarrow {p}0 \end{aligned}$$

(21)

for $j=0,1$. We express $\sqrt{n}\{\hat{\varLambda }_{ij}^C(t)-\varLambda _{ij}^C(t)\}$ as

$$\begin{aligned} \sqrt{n}\left\{ \hat{\varLambda }_{ij}^C(t)-\varLambda _{ij}^C(t)\right\}= & {} \sqrt{n}\left\{ \hat{\varLambda }_{0j}^C(t)\exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_i^C\right) -\varLambda _{0j}^C(t)\exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_i^C\right) \right\} \nonumber \\&+\sqrt{n}\left\{ \varLambda _{0j}^C(t)\exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_i^C\right) -\varLambda _{0j}^C(t)\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_i^C\right) \right\} .\nonumber \\ \end{aligned}$$

(22)

Using a Taylor expansion,

$$\begin{aligned}&\sqrt{n}\left\{ \varLambda _{0j}^C(t)\exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_i^C\right) -\varLambda _{0j}^C(t)\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_i^C\right) \right\} \nonumber \\&\quad =\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_i^C\right) \varLambda _{0j}^C(t){\mathbf {X}}_i^{CT}\sqrt{n}(\hat{{\varvec{\theta }}}_j-{\varvec{\theta }}_j)+o_p(1). \end{aligned}$$

(23)

By algebra, a Taylor expansion around ${\varvec{\theta }}_j$, the Law of Large Number, the consistency of $\hat{{\varvec{\theta }}}_j$, and (21),

$$\begin{aligned}&\sqrt{n}\left\{ \hat{\varLambda }_{0j}^C(t)\exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_i^C\right) -\varLambda _{0j}^C(t)\exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_i^C\right) \right\} \nonumber \\&\quad =\sqrt{n}\left\{ \int _0^t\frac{\sum _{l=1}^ndN_{lj}^C(s)}{\sum _{k=1}^nY_{kj}(s)\exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_k^C\right) }-\int _0^t\frac{\sum _{l=1}^ndN_{lj}^C(s)}{\sum _{k=1}^nY_{kj}(s)\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_k^C\right) }\right. \nonumber \\&\qquad \left. +\sum _{l=1}^n\int _0^t\frac{dM_{lj}^C(s)}{\sum _{k=1}^nY_{kj}(s)\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_k^C\right) }\right\} \exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_i^C\right) \nonumber \\&\quad =\sqrt{n}\left[ -\left\{ \int _0^t\bar{{\mathbf {X}}}_j^C(s;{\varvec{\theta }}_j)\frac{\sum _{l=1}^ndN_{lj}^C(s)}{\sum _{k=1}^nY_{kj}(s)\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_k^C\right) }\right\} ^T(\hat{{\varvec{\theta }}}_j-{\varvec{\theta }}_j)\right. \nonumber \\&\qquad \left. +\sum _{l=1}^n\int _0^t\frac{dM_{lj}^C(s)}{\sum _{k=1}^nY_{kj}(s)\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_k^C\right) }\right] \exp \left( \hat{{\varvec{\theta }}}_j^T{\mathbf {X}}_i^C\right) +o_p(1)\nonumber \\&\quad =-\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_i^C\right) \left\{ \int _0^t\bar{{\mathbf {x}}}_j(s;{\varvec{\theta }}_j)d\varLambda _{0j}^C(s)\right\} ^T\sqrt{n}(\hat{{\varvec{\theta }}}_j-{\varvec{\theta }}_j)\nonumber \\&\qquad +n^{-1/2}\sum _{l=1}^n\int _0^t\frac{dM_{lj}^C(s)}{r_{Cj}^{(0)}(s;{\varvec{\theta }}_j)}\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_i^C\right) +o_p(1). \end{aligned}$$

(24)

Combining (20) (22), (23) and (24), we get

$$\begin{aligned} \sqrt{n}\left\{ \hat{\varLambda }_{ij}^C(t)-\varLambda _{ij}^C(t)\right\}= & {} K_{ij}^T(t;{\varvec{\theta }}_j)\left\{ \varOmega _j^C({\varvec{\theta }}_j)\right\} ^{-1}n^{-1/2}\sum _{k=1}^nU_{kj}^C({\varvec{\theta }}_j)\nonumber \\&+\exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_i^C\right) n^{-1/2}\sum _{k=1}^n\int _0^t\frac{dM_{kj}^C(s)}{r_{Cj}^{(0)}(s;{\varvec{\theta }}_j)}+o_p(1),\qquad \end{aligned}$$

(25)

where $K_{ij}(t;{\varvec{\theta }}_j)=\int _0^t\{{\mathbf {X}}_i^C-\bar{{\mathbf {x}}}_j^C(s;{\varvec{\theta }}_j)\}d\varLambda _{ij}^C(s)$.

Now consider $W_a(t;\hat{{\varvec{\alpha }}},\hat{{\varvec{\varLambda }}}^C)-W_a(t;{\varvec{\alpha }},\hat{{\varvec{\varLambda }}}^C)$ in (16). Using Taylor expansion around ${\varvec{\alpha }}$, root-n consistency of $\hat{\varLambda }_{ij}^C(\cdot )$, the Law of Large Number and condition (i), then substituting (19), after a lot of algebra, we obtain

$$\begin{aligned}&W_a(t;\hat{{\varvec{\alpha }}},\hat{{\varvec{\varLambda }}}^C)-W_a(t;{\varvec{\alpha }},\hat{{\varvec{\varLambda }}}^C)=\{B_1(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\nonumber \\&\quad -B_0(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\}^TV_Z^{-1}({\varvec{\alpha }})n^{-1/2}\sum _{i=1}^n{\varvec{\psi }}_i^Z({\varvec{\alpha }})+o_p(1), \end{aligned}$$

(26)

where

$$\begin{aligned} B_j(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} \int _0^t w(s) \frac{(-1)^{1-j}\sum _{k=0}^1D_{1-k}(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)G_k(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{D^2(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)} dQ_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\\&+\int _0^tw(s)\frac{(-1)^jD_{1-j}(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{D(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}d\xi _j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C),\\ G_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} E\left[ \tilde{{\mathbf {X}}}_k^ZY_{kj}(s)\exp \left\{ \varLambda _{kj}^C(s-)\right\} \left\{ p_{kj}^{-1}({\varvec{\alpha }})-1\right\} \right] ,\\ dQ_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} E\left[ \frac{\exp \left\{ \varLambda _{ij}^C(s-)\right\} dN_{ij}(s)}{p_{ij}({\varvec{\alpha }})}\right] \end{aligned}$$

and

$$\begin{aligned} d\xi _j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)=E\left[ \tilde{{\mathbf {X}}}_i^Z\exp \left\{ \varLambda _{ij}^C(s-)\right\} \left\{ p_{ij}^{-1}({\varvec{\alpha }})-1\right\} dN_{ij}(s)\right] \end{aligned}$$

for $j=0,1$.

Next consider $W_a(t;{\varvec{\alpha }},\hat{{\varvec{\varLambda }}}^C)-W_a(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)$ in (16). Using Taylor expansions around $\varLambda _{ij}^C(\cdot )$ $(i=1,\ldots ,n,j=0,1)$, the Law of Large Number and condition (i), then substituting (25), after a lot of algebra, we obtain

$$\begin{aligned}&W_a(t;{\varvec{\alpha }},\hat{{\varvec{\varLambda }}}^C)-W_a(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\nonumber \\&\quad =F_0^T(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\left\{ \varOmega _0^C({\varvec{\theta }}_0)\right\} ^{-1}n^{-1/2}\sum _{i=1}^nU_{i0}^C({\varvec{\theta }}_0)\nonumber \\&\qquad -F_1^T(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\left\{ \varOmega _1^C({\varvec{\theta }}_1)\right\} ^{-1}n^{-1/2}\sum _{i=1}^nU_{i1}^C({\varvec{\theta }}_1)\nonumber \\&\qquad +n^{-1/2}\sum _{i=1}^n\int _0^{t}L_0(s,t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\frac{dM_{i0}^C(s)}{r_{C0}^{(0)}(s;{\varvec{\theta }}_0)}\nonumber \\&\qquad -n^{-1/2}\sum _{i=1}^n\int _0^{t}L_1(s,t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\frac{dM_{i1}^C(s)}{r_{C1}^{(0)}(s;{\varvec{\theta }}_1)}+o_p(1), \end{aligned}$$

(27)

where

$$\begin{aligned} F_j(t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} \int _0^t w(s)\left[ \frac{H_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)D_{1-j}(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{D^2(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}dQ_{1-j}(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\right. \\&+\frac{H_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)D_{1-j}(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{D^2(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}dQ_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\\&\left. -\frac{D_{1-j}(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{D(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}dJ_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C) \right] ,\\ H_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} E\left[ K_{kj}(s-;{\varvec{\theta }}_j)\frac{\exp \left\{ \varLambda _{kj}^C(s-)\right\} Y_{kj}(s)}{p_{kj}({\varvec{\alpha }})}\right] ,\\ dJ_j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} E\left[ K_{kj}(s-;{\varvec{\theta }}_j)\frac{\exp \left\{ \varLambda _{kj}^C(s-)\right\} dN_{kj}(s)}{p_{kj}({\varvec{\alpha }})}\right] ,\\ L_j(s,t;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} \int _s^t w(u)\left[ \frac{\gamma _j(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)D_{1-j}(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{D^2(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}dQ_{1-j}(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\right. \\&+\frac{\gamma _j(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)D_{1-j}(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{D^2(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}dQ_j(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)\\&\left. -\frac{D_{1-j}(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}{D(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C)}d\zeta _j(u;{\varvec{\alpha }},{\varvec{\varLambda }}^C) \right] ,\\ \gamma _j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)= & {} E\left[ \exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_k^C\right) \frac{\exp \left\{ \varLambda _{kj}^C(s-)\right\} Y_{kj}(s)}{p_{kj}({\varvec{\alpha }})}\right] \end{aligned}$$

and

$$\begin{aligned} d\zeta _j(s;{\varvec{\alpha }},{\varvec{\varLambda }}^C)=E\left[ \exp \left( {\varvec{\theta }}_j^T{\mathbf {X}}_k^C\right) \frac{\exp \left\{ \varLambda _{kj}^C(s-)\right\} dN_{kj}(s)}{p_{kj}({\varvec{\alpha }})}\right] \end{aligned}$$

for $j=0,1$.

Finally, substituting (18), (26) and (27) into (16) completes the proof of Theorem 2.

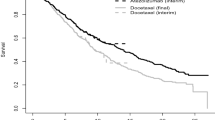
Appendix B: Assessment of the Cox models for censoring time of the SRTR data

See Fig. 3.

Fig. 3

Cox–Snell residual plots for the Cox models for censoring time of KA recipients (solid line) and of SPK recipients (dashed line)