Abstract
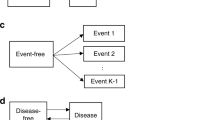
Many diseases, especially cancer, are not static, but rather can be summarized by a series of events or stages (e.g. diagnosis, remission, recurrence, metastasis, death). Most available methods to analyze multi-stage data ignore intermediate events and focus on the terminal event or consider (time to) multiple events as independent. Competing-risk or semi-competing-risk models are often deficient in describing the complex relationship between disease progression events which are driven by a shared progression stochastic process. A multi-stage model can only examine two stages at a time and thus fails to capture the effect of one stage on the time spent between other stages. Moreover, most models do not account for latent stages. We propose a semi-parametric joint model of diagnosis, latent metastasis, and cancer death and use nonparametric maximum likelihood to estimate covariate effects on the risks of intermediate events and death and the dependence between them. We illustrate the model with Monte Carlo simulations and analysis of real data on prostate cancer from the SEER database.






Similar content being viewed by others
References
American Cancer Society (2016) Cancer facts and figures 2016. American Cancer Society, Atlanta
Andersen PK, Hansen LS, Keiding N (1991) Non-and semi-parametric estimation of transition probabilities from censored observation of a non-homogeneous Markov process. Scand Stat 18(2):153–167
Andersen PK, Keiding N (2002) Multi-state models for event history analysis. Stat Methods Med Res 11(2):91–115
Biki B, Mascha E, Moriarty DC, Fitzpatrick JM, Sessler DI, Buggy DJ (2008) Anesthetic technique for radical prostatectomy surgery affects cancer recurrence: a retrospective analysis. J Am Soc Anesthesiol 109(2):180–187
Chen YH (2009) Weighted Breslow-type and maximum likelihood estimation in semiparametric transformation models. Biometrika 96(3):591–600
Chen YH (2012) Maximum likelihood analysis of semicompeting risks data with semiparametric regression models. Lifetime Data Anal 18(1):36–57
Clayton DG (1978) A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 65(1):141–151
Fine JP, Gray RJ (1999) A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc 94(446):496–509
Fine JP, Jiang H, Chappell R (2001) On semi-competing risks data. Biometrika 88(4):907–919
Govindarajulu US, Lin H, Lunetta KL, D’Agostino R (2011) Frailty models: applications to biomedical and genetic studies. Stat Med 30(22):2754–2764
Hougaard P, Hougaard P (2000) Analysis of multivariate survival data, vol 564. Springer, New York
Hu C, Tsodikov A (2014a) Joint modeling approach for semicompeting risks data with missing nonterminal event status. Lifetime Data Anal 20(4):563–583
Hu C, Tsodikov A (2014b) Semiparametric regression analysis for time-to-event marked endpoints in cancer studies. Biostatistics 15(3):513–525
Kalbfleisch JD, Prentice RL (2011) The statistical analysis of failure time data, vol 360. Wiley, Hoboken
Liu L, Wolfe RA, Huang X (2004) Shared frailty models for recurrent events and a terminal event. Biometrics 60(3):747–756
Mehlen P, Puisieux A (2006) Metastasis: a question of life or death. Nat Rev 6:449–458
Meira-Machado L, de Uña-Álvarez J, Cadarso-Suárez C (2006) Nonparametric estimation of transition probabilities in a non-markov illness-death model. Lifetime Data Anal 12(3):325–344
Neeman E, Ben-Eliyahu S (2013) Surgery and stress promote cancer metastasis: new outlooks on perioperative mediating mechanisms and immune involvement. Brain Behav Immun 30:S32–S40
Nelsen RB (1999) An introduction to copulas. Springer, Berlin
Nielsen GG, Gill RD, Andersen PK, Sørensen TIA (1992) A counting process approach to maximum likelihood estimation in frailty models. Scand J Stat 19(1):25–43
Oakes D (1989) Bivariate survival models induced by frailties. J Am Stat Assoc 84(406):487–493
O’Reilly MS, Holmgren L, Shing Y, Chen C, Rosenthal RA, Moses M, Lane WS, Cao Y, Sage EH, Folkman J (1994) Angiostatin: a novel angiogenesis inhibitor that mediates the suppression of metastases by a lewis lung carcinoma. Cell 79(2):315–328
Peng L, Fine JP (2007) Regression modeling of semicompeting risks data. Biometrics 63(1):96–108
Smolle J, Soyer HP, Smolle-Jüttner F, Rieger E, Kerl H (1997) Does surgical removal of primary melanoma trigger growth of occult metastases? An analytical epidemiological approach. Dermatol Surg 23(11):1043–1046
Tsodikov A (2003) Semiparametric models: a generalized self-consistency approach. J R Stat Soc Ser B Stat Methodol 65(3):759–774
Xu J, Kalbfleisch JD, Tai B (2010) Statistical analysis of illness-death processes and semicompeting risks data. Biometrics 66(3):716–725
Zeng D, Lin D (2006) Efficient estimation of semiparametric transformation models for counting processes. Biometrika 93(3):627–640
Acknowledgements
This research was supported by National Cancer Institute’s grants U01CA199338 (CISNET) and P50CA186786 (SPORE).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Tran, Q., Kidwell, K.M. & Tsodikov, A. A joint model of cancer incidence, metastasis, and mortality. Lifetime Data Anal 24, 385–406 (2018). https://doi.org/10.1007/s10985-017-9407-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10985-017-9407-2