Abstract
Context
Resource selection functions are powerful tools for predicting habitat selection of animals. Recently, machine-learning methods such as random forest have gained popularity for predicting habitat selection due to their flexibility and strong predictive performance.
Objectives
We tested two methods for predicting continental-scale, second-order habitat selection of a wide-ranging large carnivore, the mountain lion (Puma concolor), to support continent-wide conservation management, including estimating abundance, and to predict habitat suitability for recolonizing or reintroduced animals.
Methods
We compared a generalized linear model (GLM) and a random forest model using GPS location data from 476 individuals across 20 study sites in the western USA and Canada and remotely-sensed landscape data. We internally validated models and examined their ability to correctly classify used and available points by calculating area under the receiver operating characteristics (AUC). We performed leave-one-out (LOO) out-of-sample tests of predictive strength on both models.
Results
Both models suggested that mountain lions select for steeper slopes, areas closer to water, and with higher normalized difference vegetation index (NDVI), and against variables associated with human impact. The random forest model (AUC = 0.94) demonstrated that mountain lion habitat can be accurately predicted at continental scales, outperforming the traditional GLM model (AUC = 0.68). Our LOO validation provided similar results (x̄ = 0.93 for the random forest and x̄ = 0.65 for the GLM).
Conclusions
We found that the added flexibility of the random forest model provided deeper insights into how individual covariates impacted habitat selection across diverse ecosystems. Our LOO analyses suggested that our model can predict mountain lion habitat selection in unoccupied areas or where local data are unavailable. Our model thus provides a tool to support discussions and analyses relevant to continent-wide mountain lion conservation and management including estimating metapopulation abundance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In ecological modeling, we choose between the distinct goals of inference or prediction (James et al. 2013; Bzdok and Ioannidis 2019). The goal of inference is to differentiate between alternative a priori hypotheses, which requires low variance to determine coefficients that are non-zero. In contrast, prediction seeks to minimize mean squared errors to best forecast new observations (James et al. 2013; Tredennick et al. 2021). When modeling animal habitat relationships, for example, the difference can be expressed as “what” or “why” versus “where”. Inference seeks to understand “what” constitutes habitat (i.e., what features of the landscape do animals select) or “why” an animal uses a particular habitat. In contrast, prediction seeks to understand “where” habitat occurs (i.e., where on the landscape do animals prefer to live). The question of where is fundamental to numerous ecological and conservation management activities. For example, predicting species distribution might be the basis for estimating abundance (Jędrzejewski et al. 2018), predicting future use by recolonizing or reintroduced species (Winkel et al. 2023), or guiding strategic investment for species conservation management or interventions (Li et al. 2017). Generally, models with high flexibility exhibit lower interpretability but are more suited to prediction (Bzdok and Ioannidis 2019). When the goal is prediction, Westphal and Brannath (2020) recommend comparing multiple models and then choosing the one with the highest predictive strength, rather than the most parsimonious, as is characteristic when the goal is inference.
Resource selection functions (RSF) are a common approach to predicting the probability of an animal’s use of different landscape traits, such as elevation, terrain ruggedness, or variations in vegetation (Manly et al. 2002). Typically, RSFs are performed using generalized linear models (GLM) but more recently, ecologists are increasingly turning to machine-learning algorithms, namely, a popular technique known as random forest (Breiman 2001; Shoemaker et al. 2018; Bohnett et al. 2020). Random forest models are not bound by linearity, are well suited to include a large numbers of covariates, and can detect complex relationships and interactions. In addition, the bootstrapped structure of random forest models decreases the problematic issue of correlated data commonly associated with wildlife movement data (Breiman 2001; Fleming et al. 2015). Random forest models should apply well to the habitat selection behavior of wild animals (Shoemaker et al 2018); however, their performance appears to suffer with unbalanced presence-absence datasets in which absences outnumber detections (Chiaverini et al. 2023).
Mountain lions (Puma concolor) are a generalist carnivore that occupy diverse habitats ranging from mountains, to jungles, to deserts. Historically, they ranged from central Canada to the southern tip of South America, but following range contraction due to intense persecution, they remain absent in what was historic range in the eastern USA and Canada (Yovovich et al. 2023) as well as portions of Latin America (Nielsen et al. 2015). Mountain lions are predominantly managed as a game species in the USA and Canada at the state or provincial level, hindering our ability to estimate their abundance or any fitness metric that might support conservation strategies or management decisions at larger scales (Elbroch et al. 2022). Nevertheless, mountain lions have seen recovery into new and historic range in the USA and Canada over the last 50 years (Papouchis 2004), resulting in significant interest in mapping their potential use of historic range as well as novel habitats like desert and boreal ecosystems where they were previously absent or at very low density but are now colonizing due to changes in human attitudes (Benson et al. 2023) habitat and prey distributions (e.g., bighorn sheep (Ovis canadensis), Berger and Wehausen 1991; woodland caribou (Rangifer tarandus caribou), White et al. 2020). As an obligate carnivore, the foremost resource that mountain lions depend on is ungulate prey (Logan and Sweanor 2001; Lendrum et al. 2014), but there may also be abiotic landscape traits that affect mountain lion fitness, such as rugged terrain important for rest and thermoregulation (Kusler et al. 2017), or specific habitat where preferred ungulate prey is hunted (Cristescu et al. 2019). As such, analysis of mountain lion resource selection should include abiotic landscape traits alongside metrics that may indicate prey distribution and abundance such as primary productivity (Walters 2001).
As a wide-ranging species, mountain lions occupy large areas where no data has been collected making habitat modeling in those areas difficult. Our aim was to compare two methodologies for projecting mountain lion habitat in areas where no data exists. We created a classical GLM alongside a random forest model and tested both for predictive strength using out-of-sample validation. Our first goal was to test which method created the best predictive map of second order habitat selection by mountain lions across North America. This map could be used as a basis for estimating local and continental-scale abundance (Jędrzejewski et al. 2018) or to inform conservation strategies, such as corridor mapping (Winkel et al. 2023), determining the likeliness of successful recolonization (Yovovich et al. 2023), or predicting interactions with rare prey species such as woodland caribou as they expand northward due to climate change and new distributions of the mountain lion’s primary prey, deer (Odocoileus spp.; White et al. 2020). By sampling multiple study areas across diverse ecoregions, we aimed to identify the most robust effects that different landscape traits have on mountain lion resource selection. Our second goal was to determine whether mountain lion habitat selection is consistent across ecoregions at the continental scale. We employed out-of-sample validation to test whether our model could be used to accurately identify habitat in un-sampled regions where intensive studies have not occurred, due to costs or other feasibility, or in areas of historic but currently unoccupied mountain lion range (i.e., the eastern USA; Winkel et al. 2023, Yovovich et al. 2023).
Study area
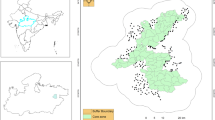
We compiled mountain lion global positioning system (GPS) location data from multiple state and federal agencies, universities, and non-governmental organizations (NGOs) across the USA and Canada. These data span the desert southwest, coastal chaparral, montane, and alpine zones of the Rocky Mountains, and the temperate rain forests of the Pacific Northwest. Our study area is thus best represented as current North American mountain lion range excluding Mexico (Fig. 1; Hornocker and Negri 2010; Nielsen et al. 2015). Elevations in the study area ranged from sea level to over 4,200 m, annual precipitation ranged from 13 cm in southern California to > 500 cm in the Pacific Northwest, and land-use varied from highly urban areas to remote wilderness. As such, they cover much of the variability likely to be encountered by mountain lions across North America.
Methods
Overview
Both GLM and random forest compare actual animal locations to available or pseudo absence locations at relevant spatial scales to predict habitat use based on the variables contained in the model. At small scales, an RSF may show how an animal uses areas within its home range, but a small analytical scale may not be appropriate in predicting a species’ first or second order selection (i.e., selection by all animals across its full range, or selection of an entire population of animals; Johnson 1980) (Boyce 2006, DeCesare et al. 2014).
Both GLM and random forest methods can be used to map the predicted probability of use based upon disproportionate selection for habitat characteristics. GLMs employ the maximum likelihood method of logistic regression to compare use to availability, whereas random forest classification tallies votes from bootstrapped decision trees. First, a number of trees are created from bootstrapped data (commonly 500 trees), then an observation is predicted by each tree. The number of trees predicting “used” points is divided by the number of trees predicting “available” points to achieve a probability (e.g., 50 votes for “use” of a particular point and 450 votes for non-use, or “available” point, would produce an 11% probability of use; Shoemaker et al. 2018) (Table 1).
Data
From 2002 onwards, researchers have deployed GPS collars on mountain lions which provide accurate locations and typically cover the diel period with multiple fixes per animal per day. For our analyses, we compiled 1.3 million location points from 476 collared animals from 20 different study sites across the USA and Canada (Table 2), and restricted the data to GPS collar locations from independent, resident adults using the CTMM package in R (Calabrese et al. 2016; R core team 2021). Most data did not include position dilution of precision or other measures of precision and we therefore did not remove points based on these metrics. We did, however, remove some locations we judged as clearly erroneous (i.e., with single point data errors > 100 miles from the previous point in < 4 h).
Advances in technology have led to decreasing fix intervals in GPS data which increases autocorrelation and can bias parameter estimates (Alston et al. 2023). However, large sample sizes and external validation counteract the problem of autocorrelation, especially in cases where the goal is prediction rather than inference (Northrup et al. 2013). Therefore, we did not filter the data for the purpose of counteracting autocorrelation but instead relied on the large sample size and a rigorous method of external validation. In addition, the bootstrapping step of the random forest acts as a thinning mechanism to decorrelate autocorrelated data (Breiman 2001).
Spatial covariates
Our goal was to create a predictive resource selection model as opposed to a more traditional test of competing hypotheses in a multi-model context. A complete list of all variables considered is shown in Table 1. Following ecological theory (Power 1992), we categorized covariates into two broad categories, which we called “bottom-up” or “top-down” effects.
Mountain lions depend on their prey which are tied to primary productivity (Walters 2001) so a main bottom-up driver will be primary productivity as represented by the normalized difference vegetation index (NDVI; Pettorelli et al. 2005). NDVI is calculated from the ratio of red to near-infrared (NIR) reflectance (NDVI = (NIR-RED)/(NIR + RED) (Myneni et al. 1995) and measures “greenness” of vegetation which is tied to digestible energy for herbivores (Garroutte et al. 2016). As an ambush predator that utilizes cover for hunting, structural habitat traits are important to a mountain lion’s ability to catch prey (Cristescu et al. 2019, Coon et al. 2020). We used several layers from MODIS (DiMiceli et al. 2015) including forest, shrub cover, and non-vegetated areas. These layer values represent the proportion of the pixel at 250 m resolution covered by that vegetation type. We acquired these data from satellite imagery using the Google Earth Engine platform (Gorelick et al. 2017). We also included other bottom-up covariates representing abiotic landscape traits that might impact hunting success and other fitness, such as aspect (converted from degrees to a continuous measure using a cosine transformation), slope (degrees) and elevation.
Mountain lions are also impacted by top-down effects such as human values, impact and alterations of the landscape (Dickson et al. 2005, Wilmers et al. 2013, Wolfe et al. 2015, Benson et al. 2019, 2023) although some human-altered landscapes may be to their benefit (Coon et al. 2019). Therefore, we included covariates measuring potential human impact (Table 1).
We used human density and several human impact layers produced by the Wildlife Conservation Society (2022) including roads, land-use, and infrastructure. These layers are a weighted calculation of impact based on multiple factors and utilize an exponential decay function to decrease the value of the impact at distance to the feature. For instance, the roads impact layer included weighted values scaled from the lowest impact which includes footpaths and cycle-ways to higher impact values for motorized roads and major highways (Wildlife Conservation Society 2022).
We standardized all variables using a Z transformation. To reduce the total number of candidate variables and to produce a single candidate set, we first screened variables for significance (p < 0.05) in univariate models (Hosmer Jr et al. 2013). We then screened covariates for collinearity, removing correlated variables |> 0.8| from the candidate set based on lower relative univariate r2 value. We chose a high correlation threshold because overfitting is less of an issue in cases of prediction, especially when sample size is sufficient (Hawkins 2004; Steyerberg 2019). The result of this screening process was a set of candidate variables that we then used to model resource selection using the two methods (see below).
Resource selection modeling
To model second order selection, habitat traits within an animal’s home range are compared to the surrounding landscape (Johnson 1980). In our model, used points were GPS locations for each mountain lion while available points were randomly generated pseudo absences. We used the adehabitatHR package in R for the following tasks (Calenge 2006; R core team 2021): 1) We set the spatial extent of available points specific to each study site by creating 99% adaptive kernel polygons using the combined GPS locations from all independent mountain lions that were marked with GPS collars in each research project. Because research projects define study sites differently and often in non-biologically relevant ways, it was important to create standardized available habitat for each site. 2) We matched used and available points from each study site at a 1:1 ratio. We used the raster package in R to extract landscape (i.e., covariate) values from the used and available points (Hijmans 2022; R core team 2021).
Generalized linear mixed model
To account for individual and geographical variation, we included individual animals and study sites as random effects (Gillies et al. 2006). The model took the form for location i, animal j, and study area k:
where β1, β2, and β3 are covariate fixed effects and \({\zeta }_{jk}\) accounts for random variation at the intercept for individual animals and study areas. We used the lme4 package in R to fit this model (Bates et al. 2015; R core team 2021).
Random forest model
We used the randomForest package in R (Liaw and Wiener 2002; R core team 2021) to build a random forest model using the same pool of habitat variables and used and available points as for the GLM above. Although random forest is well suited for large numbers of highly correlated variables (Breiman 2001), we chose to use the same pool of variables for greater comparability to the GLM. Following guidance in Probst et al. (2019), we tuned the model to 1000 trees and 6 variables at each split using the tuneRF function from the randomForest package.
Model validation and method comparison
We validated both models using internal and external methods. We internally validated the models and examined their ability to correctly classify used and available points by calculating area under the receiver operating characteristic (AUC) curve in R (Spackman 1989; R core team 2021). An AUC score of > 0.7 is generally considered acceptable and a score of > 0.8 is considered excellent (Hosmer Jr et al. 2013). We tested the variable inflation factor (VIF) to ensure no two variables were excessively correlated (i.e., VIF < 5). Ecological data often contain dependence structures (i.e., correlations within individual animals or study sites), therefore non-random, blocked, cross-validation approaches should be used to validate the models more rigorously (Roberts et al. 2017). To accomplish this, we performed a leave-one-out (LOO) external validation by excluding each study site from the model and projecting the model to that same site to measure its predictive ability. We first reclassified the RSF into 10 equal area bins based on probability of use, and then summed the number of used points in each of 10 bins. We then conducted a Spearman’s rank correlation test to see if used points fell in the higher probability bins (Fielding and Bell 1997; Boyce et al. 2002). We examined the output of the two models by comparing the variable importance for the random forest model and scaled and centered effect size for the GLM. Finally, we used the raster package in R to project the top model to all of the historic mountain lion range to create a probability map of mountain lion habitat (30 m cells; Hijmans 2022; R core team 2021).
Results
Candidate covariates
After initial screening, our final candidate set of covariates included: distance to water, NDVI, slope, forest cover, shrub cover, non-vegetation, elevation, aspect, roads impact, land-use, infrastructure, and human density. Gross Primary Productivity was removed due to excessive correlation to NDVI.
Generalized linear model
In the final multivariate GLM, NDVI, slope, and shrub cover had positive effects on mountain lion resource selection while forest cover, elevation, road impact, infrastructure, non-vegetation, land-use, and population density had negative effects (Table 3). Distance to water also showed a negative effect, indicating a higher probability of use closer to water sources.
Random forest model
The random forest variable plots show similar effects to the GLM with habitat covariates exhibiting positive responses, and human-influence covariates generally exhibiting negative responses (Fig. 5). Interpreting the variable plots from the random forest model is more complex as compared to the GLM beta estimates, due to the inherent non-linearity of random forest. For example, mountain lions generally showed higher probability of use for areas at low elevations, but probability declines at very low elevations (i.e.at 0 elevation or sea level). Mountain lions exhibited a lower probability of use for areas lacking footpaths or trails, higher probability of use for low-impact roads (i.e. footpaths and dirt roads), and then again a lower probability of use for high-impact roads (i.e. paved roads and highways), aligning well for what is known about their behavior (e.g. Dickson et al. 2005). Most variables exhibited a “humped” shape (e.g. NDVI, slope, forest, non-vegetated area, and shrub cover), indicating that mountain lions varied their probability of use across the range of values for these variables, rather than exhibited a single consistent relationship and probability of use.
Comparative analysis of GLM and random forest models
The random forest outperformed the GLM, with AUC values of 0.68 for the GLM and 0.94 for the random forest (Fig. 2). The mean Spearman’s rho score from our LOO validation was 0.65 for the GLM and 0.93 for the random forest (Fig. 3). Within the GLM framework, we found support for all hypothesized effects except elevation and forest (Table 3). We predicted elevation and forest cover would show positive effects on mountain lion selection however both showed negative effects on probability of use. Random forest partial dependency variable plots show similar responses of our selected variables (Fig. 5). Probability of use declines overall with increased elevation in both models. Probability of use increases slightly with forest cover but declines near the maximum values of percent forest per pixel. This is corroborated by the negative effect for forest cover in the GLM.
Comparison of leave-one-out external validation of GLM and random forest mountain lion resource selection models from 20 separate sites (see also Fig. 1) between 2002 to 2020
Variable importance and effect sizes
The random forest and GLM show similar ranking of variable importance and effect size (Fig. 4). Both show elevation and NDVI as the most important variables. A notable separation between the models occurs with the variables, land-use impact and human population density. These variables exhibit the third and fourth largest effect sizes in the GLM but are ranked much lower (i.e. tenth and eleventh) by the random forest (Fig. 5).
Model projection
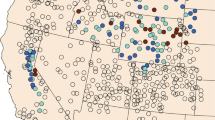
We projected the random forest model to create a map depicting probable mountain lion use or occurrence (Fig. 6). Higher probability areas appear closely tied to rugged, wilderness areas and away from flat farmland and urban areas. The eastern U.S. is characterized by an abundance of high-probability habitat.
Discussion
In predicting continental-scale second-order resource selection of a cryptic carnivore, random forest models (AUC = 0.94) outperformed GLM models (AUC = 0.68), highlighting the strength of random forest methods in predicting non-linear, complex interactions characteristic of animal habitat use and selection. Mountain lion resource selection was positively associated with bottom-up factors such as NDVI and shrub cover, and negative associations with all top-down, anthropogenic factors, including human population density, land-use and infrastructure. Our LOO analyses highlighted the strength of our model in predicting mountain lion habitat selection across ecoregions and in novel areas into which they are expanding, as well as their potential use of historic range currently unoccupied. Our model provides a powerful tool to aid conservation practitioners in transcending the current limitation of state- or provincial-scale assessments of the species, and one that supports discussions and analyses of continent-wide, cross-jurisdictional conservation and management of mountain lions (Elbroch et al. 2022).
Discrepancies between GLM and random forest models
We found general agreement between the random forest and GLM models, with regards to the relative importance of the various covariates tested (Fig. 4). The added flexibility of random forest models, however, provided deeper insights when interpreting the influence of covariates on habitat selection. For example, where the GLM only revealed a small negative effect associated with roads, the random forest showed a stronger and more complex relationship; mountain lions increased their selection for low-impact roads such as footpaths but decreased selection for high-impact roads, such as paved motorways and highways (Fig. 5). The random forest also showed slightly increased selection for forest cover with decreased selection for the maximum values of forest cover. This is likely due to mountain lions favoring mixed vegetation and partially open canopies where prey and hunting opportunities are higher.
Nevertheless, when comparing the effect sizes of the GLM with the variable importance ranking of the random forest, land-use impact and human population density ranked very differently (Fig. 4). These variables showed large effect sizes in the GLM but low importance in the random forest, due to differences in model structure. The GLM is bound by linearity and requires interaction effects between predictors to be specified, whereas random forest allows for non-linear relationships and inherently accounts for interactions among features in the construction of decision trees. A variable that appears less important in a GLM might be identified as more important in random forest due to its contribution to reducing prediction error when used in conjunction with other variables.
Addressing model overfitting and external validation
As with other complex models, there is risk of random forest overfitting predictive models. This can be examined with rigorous external validation as performed here with the “leave-one-out” method. As stated previously, ecological data often contain dependence structures so “blocked” external validation is needed; in this case, leaving out each study site, some of which represented entire ecoregions. For example, the model performed well at predicting mountain lion habitat use in the desert southwest, even when data from the desert southwest was omitted from model building. This suggests that the model did not overfit and is transferable to regions where no data are available. In addition, an advantage of a large-scale analysis such as this is that the problem of overfitting is mitigated by using data spanning a range of environmental conditions. An RSF built from one study site may overfit to unique aspects of that region whereas an RSF built from multiple sites will better capture the true habitat selection behavior of the species and can more confidently be extrapolated to other areas once externally validated.
Implications for conservation and management
Our model predicted an abundance of high-quality mountain lion habitat in their historic range in the eastern USA and Canada. In fact, our predictive map would suggest that portions of the eastern USA are superior habitat in comparison to the west. This is likely due to NDVI being the strongest driver of mountain lion habitat selection in our model and that the eastern USA contains very high relative NDVI values. Nevertheless, even considering the current human footprint in the more densely populated eastern USA, our model supports other analyses based on expert opinion (e.g., Winkel et al. 2023, Yovovich et al. 2023) which predict significant mountain lion habitat beyond their current range today.
Limitations and future directions
Our analysis lays the groundwork for population prediction, utilizing a habitat-based approach to estimate mountain lion densities (e.g. Boyce and McDonald 1999). By establishing a correlation between habitat and densities, this model can be used to create defensible assessments of current mountain lion populations and holds the potential to project future densities in regions where mountain lions may recolonize. Moreover, this understanding of habitat can be utilized in formulating effective management plans tailored to specific jurisdictions (e.g. harvest setting when determined by habitat-based abundance estimates; Beausoleil et al. 2013). Leveraging the habitat map, hunted areas can be strategically categorized into low, medium, and high habitat quality zones, facilitating the development of targeted management strategies for conservation.
Our model does not assess the impacts of landscape connectivity on potential habitat selection. Large highways are an impediment for mountain lion movement (Ernest et al. 2014; Yovovich et al. 2023), and the eastern U.S., with its dense highway system may prove to be an obstacle for mountain lions trying to reach potential habitat. Although our projected model does not measure connectivity explicitly, it can be used as a base layer for connectivity modeling (Chetkiewicz and Boyce 2009). Zeller et al (2018) showed that RSF models outperform other layers when converted to resistance layers from relative probability of use.
Conclusion
Our study represents an advancement in the field of habitat selection modeling, particularly in the context of large carnivore conservation. By comparing the performance of GLM and random forest models in predicting habitat selection of mountain lions at a continental scale, we demonstrated the superiority of machine learning techniques in capturing the complexity of habitat selection behavior. The higher predictive accuracy of the random forest model underscores its potential utility in predicting habitat for mountain lions in unoccupied areas or regions lacking local data. These findings contribute to our understanding of mountain lion ecology and have broader implications for wildlife management and conservation efforts on continental scales. Our model can serve as a valuable tool for informing conservation strategies, estimating metapopulation abundance, and facilitating habitat restoration efforts for mountain lions and other wide-ranging carnivores. Additionally, our study highlights the importance of collaborative data sharing and integrating advanced machine-learning techniques into ecological research.
Data availability
The datasets generated during analysis may be made available upon reasonable request.
References
Alston JM, Fleming CH, Kays R, Streicher JP, Downs CT, Ramesh T, Calabrese JM (2023) Mitigating pseudoreplication and bias in resource selection functions with autocorrelation-informed weighting. Methods Ecol Evol 14:643–654
Bates D, Maechler M, Bolker B, Walker S (2015) Fitting linear mixed-effects models using lme4. J Stat Softw 67(1):1–48. https://doi.org/10.18637/jss.v067.i01
Beausoleil RA, Koehler GM, Maletzke BT, Kertson BN, Wielgus RB (2013) Research to regulation: cougar social behavior as a guide for management. Wildl Soc Bull 37:680–688
Benson JF, Mahoney PJ, Vickers TW, Sikich JA, Beier P, Riley SP, Ernest HB, Boyce WM (2019) Extinction vortex dynamics of top predators isolated by urbanization. Ecol Appl 29:e01868
Benson JF, Dougherty KD, Beier P, Boyce WM, Cristescu B, Gammons DJ, Garcelon DK, Higley JM, Martins QE, Nisi AC, Riley SP (2023) The ecology of human-caused mortality for a protected large carnivore. Proc Natl Acad Sci 120:e2220030120
Berger J, Wehausen J (1991) Consequences of a mammalian predator-prey disequilibrium in the Great Basin Desert. Conserv Biol 5:243–248
Bohnett E, Hulse D, Ahmad B, Hoctor T (2020) Multi-level, multi-scale modeling and predictive mapping for jaguars in the Brazilian Pantanal. Open J Ecol 10:243
Boyce MS (2006) Scale for resource selection functions. Divers Distrib 12:269–276
Boyce MS, McDonald LL (1999) Relating populations to habitats using resource selection functions. Trends Ecol Evol 14:268–272
Boyce MS, Vernier PR, Nielsen SE, Schmiegelow FK (2002) Evaluating resource selection functions. Ecol Model 157:281–300
Breiman L (2001) Random forests. Mach Learn 45:5–32
Bzdok D, Ioannidis JP (2019) Exploration, inference, and prediction in neuroscience and biomedicine. Trends Neurosci 42:251–262
Calabrese JM, Fleming CH, Gurarie E (2016) ctmm: An R package for analyzing animal relocation data as a continuous-time stochastic process. Methods Ecol Evol 7:1124–1132
Calenge C (2006) The package adehabitat for the R software: a tool for the analysis of space and habitat use by animals. Ecol Model 197:516–519
Chetkiewicz CLB, Boyce MS (2009) Use of resource selection functions to identify conservation corridors. J Appl Ecol 1036–1047
Chiaverini L, Macdonald DW, Hearn AJ, Kaszta Ż, Ash E, Bothwell HM, Can ÖE, Channa P, Clements GR, Haidir IA, Kyaw PP (2023) Not seeing the forest for the trees: Generalised linear model out-performs random forest in species distribution modelling for Southeast Asian felids. Eco Inform 75:102026
Coon CA, Mahoney PJ, Edelblutte E, McDonald Z, Stoner DC (2020) Predictors of puma occupancy indicate prey vulnerability is more important than prey availability in a highly fragmented landscape. Wildlife Biol 2020:1–12
Coon CA, Nichols BC, McDonald Z, Stoner DC (2019) Effects of land-use change and prey abundance on the body condition of an obligate carnivore at the wildland-urban interface. Landsc Urban Plan 192:103648
Cristescu B, Bose S, Elbroch LM, Allen ML, Wittmer HU (2019) Habitat selection when killing primary prey versus alternative prey species supports prey specialisation in an apex predator. J Zool 309(4):259–268
DeCesare NJ, Hebblewhite M, Bradley M, Hervieux D, Neufeld L, Musiani M (2014) Linking habitat selection and predation risk to spatial variation in survival. J Anim Ecol 83:343–352
Dellinger JA, Cristescu B, Ewanyk J, Gammons DJ, Garcelon D, Johnston P, Martins Q, Thompson C, Vickers TW, Wilmers CC, Wittmer HU (2020) Using mountain lion habitat selection in management. J Wildl Manag 84:359–371
Dickson BG, Jenness JS, Beier P (2005) Influence of vegetation, topography, and roads on cougar movement in southern California. J Wildl Manag 69:264–276
DiMiceli C, Carroll M, Sohlberg R, Kim D, Kelly M, Townshend J (2015) MOD44B MODIS/terra vegetation continuous fields yearly L3 global 250m SIN Grid V006. NASA EOSDIS land processes DAAC. https://doi.org/10.5067/MODIS/MOD44B.006. Accessed 2022-07-07
Elbroch LM, Petracca LS, O’Malley C, Robinson H (2022) Analyses of national mountain lion harvest indices yield ambiguous interpretations. Ecol Sol Evid 3:12150
Ernest HB, Vickers TW, Morrison SA, Buchalski MR, Boyce WM (2014) Fractured genetic connectivity threatens a southern California puma (Puma concolor) population. PLoS One 9:107985
Fielding AH, Bell JF (1997) A review of methods for the assessment of prediction errors in conservation presence/absence models. Environ Conserv 24:38–49
Fleming CH, Fagan WF, Mueller T, Olson KA, Leimgruber P, Calabrese JM (2015) Rigorous home range estimation with movement data: a new autocorrelated kernel density estimator. Ecology 96:1182
Garroutte EL, Hansen AJ, Lawrence RL (2016) Using NDVI and EVI to map spatiotemporal variation in the biomass and quality of forage for migratory elk in the Greater Yellowstone Ecosystem. Remote Sensing 8:404
Gillies CS, Hebblewhite M, Nielsen SE, Krawchuk MA, Aldridge CL, Frair JL, Saher DJ, Stevens CE, Jerde CL (2006) Application of random effects to the study of resource selection by animals. J Anim Ecol 75:887–898
Gorelick N, Hancher M, Dixon M, Ilyushchenko S, Thau D, Moore R (2017) Google earth engine: planetary-scale geospatial analysis for everyone. Remote Sens Environ 202:18–27
Hawkins DM (2004) The problem of overfitting. J Chem Inf Comput Sci 44:1–12
Hijmans RJ (2022) raster: geographic data analysis and modeling. R package version 3.5–21. https://CRAN.R-project.org/package=raster. Accessed 1 June 2020
Hornocker MG, Negri S (2010) Cougar: ecology and conservation. The University of Chicago Press, Chicago
Hosmer DW Jr, Lemeshow S, Sturdivant RX (2013) Applied logistic regression, vol 398. Wiley
James G, Witten D, Hastie T, Tibshirani R (2013) An introduction to statistical learning. Springer, New York
Jędrzejewski W, Robinson HS, Abarca M, Zeller KA, Velasquez G, Paemelaere EA, Goldberg JF, Payan E, Hoogesteijn R, Boede EO, Schmidt K (2018) Estimating large carnivore populations at global scale based on spatial predictions of density and distribution–application to the jaguar (Panthera onca). PLoS One 13:3
Johnson DH (1980) The comparison of usage and availability measurements for evaluating resource preference. Ecology 61:65–71
Kusler A, Elbroch LM, Quigley H, Grigione M (2017) Bed site selection by a subordinate predator: An example with the cougar (Puma concolor) in the Greater Yellowstone Ecosystem. PeerJ 5:e4010
Lendrum PE, Elbroch LM, Quigley H, Thompson DJ, Jimenez M, Craighead D (2014) Home range characteristics of a subordinate predator: selection for refugia or hunt opportunity? J Zool 294:58–66
Li J, Alvarez B, Siwabessy J, Tran M, Huang Z, Przeslawski R, Radke L, Howard F, Nichol S (2017) Application of random forest, generalised linear model and their hybrid methods with geostatistical techniques to count data: Predicting sponge species richness. Environ Model Softw 97:112–129
Liaw A, Wiener M (2002) Classification and regression by randomforest. R News 2:18–22
Logan KA, Sweanor LL (2001) Desert puma: evolutionary ecology and conservation of an enduring carnivore. Island Press, Washington D, C., USA
Manly BF, McDonald LL, Thomas DL, McDonald TL, Erickson WP (2002) Introduction to resource selection studies. Resource selection by animals: statistical design and analysis for field studies. pp 1–15
Myneni RB, Hall FG, Sellers PJ, Marshak AL (1995) The interpretation of spectral vegetation indexes. IEEE Trans Geosci Remote Sens 33:481–486
Nielsen C, Thompson D, Kelly M, Lopez-Gonzalez CA (2015) Puma concolor. The IUCN red list of threatened species. https://doi.org/10.2305/IUCN.UK.20154.RLTS.T18868A50663436.en. Accessed 20 Feb 2021
Northrup JM, Hooten MB, Anderson CR Jr, Wittemyer G (2013) Practical guidance on characterizing availability in resource selection functions under a use–availability design. Ecology 94:1456–1463
Papouchis CM (2004) Conserving mountain lions in a changing landscape. People and predators: from conflict to coexistence, pp 219–239
Pettorelli N, Vik JO, Mysterud A, Gaillard JM, Tucker CJ, Stenseth NC (2005) Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol Evol 20:503–510
Power ME (1992) Top-down and bottom-up forces in food webs: do plants have primacy. Ecology 73:733–746
Probst P, Wright MN, Boulesteix AL (2019) Hyperparameters and tuning strategies for random forest. Wiley interdisciplinary reviews: data mining and knowledge discovery, 9:1301
R Core Team (2021) R: a language and environment for statistical computing. R foundation for statistical computing, Vienna, Austria. https://R-project.org/. Accessed 1 August 2021
Roberts DR, Bahn V, Ciuti S, Boyce MS, Elith J, Guillera-Arroita G, Hauenstein S, Lahoz-Monfort JJ, Schröder B, Thuiller W, Warton DI (2017) Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 40:913–929
Robinson HS, Ruth T, Gude JA, Choate D, DeSimone R, Hebblewhite M, Kunkel K, Matchett MR, Mitchell MS, Murphy K, Williams J (2015) Linking resource selection and mortality modeling for population estimation of mountain lions in Montana. Ecol Model 312:11–25
Shoemaker KT, Heffelfinger LJ, Jackson NJ, Blum ME, Wasley T, Stewart KM (2018) A machine-learning approach for extending classical wildlife resource selection analyses. Ecol Evol 8:3556–3569
Sikes RS, Gannon WL, Use Committee of the American Society of Mammalogists (2011) Guidelines of the American society of mammalogists for the use of wild mammals in research. J Mammal 92:235–253
Spackman KA (1989) Signal detection theory: valuable tools for evaluating inductive learning. Proceedings of the sixth international workshop on machine learning, Morgan Kaufmann, pp 160–163
Steyerberg, E.W. 2019. Overfitting and optimism in prediction models. In clinical prediction models, vol 95. Springer, Cham 112
Tredennick AT, Hooker G, Ellner SP, Adler PB (2021) A practical guide to selecting models for exploration, inference, and prediction in ecology. Ecology 102:e03336
Walters S (2001) Landscape pattern and productivity effects on source-sink dynamics of deer populations. Ecol Model 143:17–32
Westphal M, Brannath W (2020) Evaluation of multiple prediction models: A novel view on model selection and performance assessment. Stat Methods Med Res 29:1728–1745
Wildlife Conservation Society (2022) Species conservation landscapes. Available at: Github.com/SpeciesConservationLandscapes. Accessed 1 June 2020
Wilmers CC, Wang Y, Nickel B, Houghtaling P, Shakeri Y, Allen ML, Kermish-Wells J, Yovovich V, Williams T (2013) Scale dependent behavioral responses to human development by a large predator, the puma. PLoS One 8:e60590
Winkel BM, Nielsen CK, Hillard EM, Sutherland RW, LaRue MA (2023) Potential cougar habitats and dispersal corridors in Eastern North America. Landsc Ecol 38:59–75
White SC, Shores CR, DeGroot L (2020) Cougar (Puma concolor) predation on northern mountain caribou (Rangifer tarandus caribou) in central British Columbia. Can Field-Nat 134:265–269
Wolfe ML, Koons DN, Stoner DC, Terletzky P, Gese EM, Choate DM, Aubry LM (2015) Is anthropogenic cougar mortality compensated by changes in natural mortality in Utah? Insight from long-term studies. Biol Cons 182:187–196
Yovovich V, Robinson N, Robinson H, Manfredo MJ, Perry S, Bruskotter JT, Vucetich JA, Solórzano LA, Roe LA, Lesure A, Robertson J (2023) Determining puma habitat suitability in the Eastern USA. Biodivers Conserv 32:921–941
Zeller KA, Jennings MK, Vickers TW, Ernest HB, Cushman SA, Boyce WM (2018) Are all types of connectivity models created equal? Validating common connectivity approaches with dispersal data. Divers Distrib 24:868–879
Zeller KA, Vickers TW, Ernest HB, Boyce WM (2017) Multi-level, multi-scale resource selection functions and resistance surfaces for conservation planning: pumas as a case study. PLoS One 12:e0179570
Acknowledgements
Summerlee Foundation, Kaplan Graduate Award, the Carroll Petrie Foundation, and the Regina Bauer Frankenberg Foundation. HUW thanks the California Department of Fish and Wildlife (CDFW) and the California Deer Association for funding the Mendocino and Siskiyou projects. RB would like to thank Washington Department of Fish and Wildlife, and Lindsay Welfelt who helped compile WA-based GPS data for this analysis. Thank you to Montana Fish, Wildlife & Parks for providing GPS collar data. Thank you to the countless field techs and researchers whose sweat and hard work collaring mountain lions makes research like this possible. This research was supported in part by the USDA Forest Service, Rocky Mountain Research Station, Aldo Leopold Wilderness Research Institute. The findings and conclusions in this publication are those of the authors and should not be construed to represent any official USDA or US Government determination or policy. Thank you to WWF Northern Great Plains Office for funding for our project and logistical assistance and support from Rocky Boys and Ft Belknap Indian reservations. WV thanks CA State Parks, CDFW, The Nature Conservancy, San Diego County Association of Governments, San Diego Foundation, Anza Borrego Foundation, the McBeth Foundation and the Orange County Natural Communities Coalition for funding of the southern California project.
Funding
This work was supported by the Summerlee Foundation, Kaplan Graduate Award, Carroll Petrie Foundation, Washington Department of Fish and Wildlife, WWF Northern Great Plains Office, California Department of Fish and Wildlife Federal Aid and Wildlife Restoration Grant(s) F17AF00236 and F19AF00291, California Deer Association, California State Parks, The Nature Conservancy, San Diego County Association of Governments, San Diego Foundation, Anza Borrego Foundation, the McBeth Foundation, the Regina Bauer Frankenberg Foundation, USDA Forest Service, Montana Fish, Wildlife & Parks, and Orange County Natural Communities Coalition.
Author information
Authors and Affiliations
Contributions
CO, HR, ME, KZ and PB contributed to the study conception and design. Data collection was performed by CO, ME, MB, RB, BK, KK, KK, BM, QM, MM, CW, HW, and WV. Data processing and analysis was performed by CO. Majority of writing and editing was performed by CO, ME, KZ, HR and HW. All authors read and edited multiple versions of the manuscript.
Corresponding author
Ethics declarations
Ethical approval
Our research adhered to the guidelines outlined by the American Society of Mammologists (Sikes et al. 2011).
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
O’Malley, W.C., Elbroch, L.M., Zeller, K.A. et al. Machine learning allows for large-scale habitat prediction of a wide-ranging carnivore across diverse ecoregions. Landsc Ecol 39, 106 (2024). https://doi.org/10.1007/s10980-024-01903-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10980-024-01903-2