The effect of the flow and solid matrix parameters on the Nusselt number for free convection over horizontal cylinder by considering the boundary layer and local thermal non-equilibrium model

Abstract

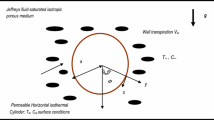
In this study, the local thermal non-equilibrium model (LTNE) and the parabolic boundary layer governing differential equations were used to investigating the effect of the flow and solid matrix parameters on the Nusselt number for free convection over a horizontal cylinder embedded in a saturated infinite packed bed. The Forchheimer–Brinkman-extended Darcy and the local thermal non-equilibrium scheme were solved by the Keller box numerical method. Using the variables of the boundary layer, the physical environment is transferred to a rectangular computational domain; then with the new variables, one order of the derivatives of the equations is reduced and the three-diagonal matrix of the coefficients is calculated. The impacts of the porosity, thermal conductivity ratio, Rayleigh number, the ratio of cylinder diameter to spherical particle diameter and Biot number parameters on the local and average Nusselt number have been studied. The obtained results showed that, the increasing Rayleigh number and porosity increase the mean Nusselt number of two phases. In such a way that increasing the porosity from 0.2 to 0.85 can increase the Nusselt of fluid by 8 times. Also, increasing the ratio of cylinder diameter to spherical particle diameter from 20 to 100 causes the mean fluid Nusselt to decrease by 64%. In addition, increasing the ratio of solid to fluid conductivity and Biot number reduces the average Nusselt of the fluid. Except for the Rayleigh number, the changes of other fluid and solid parameters did not have a significant effect on the amount of solid Nusselt.

Appendix

Some mathematical operations used in deriving equations

$$ \begin{aligned} & u = \frac{\partial \left( \psi \right)}{{\partial y}},\quad \psi = \nu \xi \sqrt[4]{{\text{Gr}}} f,\quad \xi = \frac{x}{a} ,\quad \eta = \frac{y}{a}\sqrt[4]{{\text{Gr}}} \\ & \frac{\partial \psi }{{\partial y}} = \frac{\partial \psi }{{\partial \eta }} \cdot \frac{\partial \eta }{{\partial y}} + \frac{\partial \psi }{{\partial \xi }} \cdot \frac{\partial \xi }{{\partial y}} = \frac{\partial f}{{\partial \eta }}\nu \xi \sqrt[4]{{\text{Gr}}} . \cdot \frac{{\sqrt[4]{{\text{Gr}}}}}{a} \\ & \frac{\partial \left( \psi \right)}{{\partial y}} = \frac{1}{a} \nu \xi \sqrt {{\text{Gr}}} \frac{\partial f}{{\partial \eta }} \\ & u = \nu \xi \sqrt {{\text{Gr}}} \frac{\partial f}{{\partial \eta }} \\ \end{aligned} $$

(13)

$$ \begin{aligned} & u = \frac{1}{a} \nu \xi \sqrt {{\text{Gr}}} f^{\prime} \\ & v = - \frac{\partial \left( \psi \right)}{{\partial x}} \\ & \frac{\partial \psi }{{\partial x}} = \frac{\partial \psi }{{\partial \xi }} \cdot \frac{\partial \xi }{{\partial x}} + \frac{\partial \psi }{{\partial \eta }} \cdot \frac{\partial \eta }{{\partial x}} = \frac{\partial \psi }{{\partial \xi }} \cdot \frac{1}{a} \\ & \frac{\partial \psi }{{\partial \xi }} = \left( {\frac{\partial f}{{\partial \xi }}\nu \xi \sqrt[4]{{\text{Gr}}} + f\nu \sqrt[4]{{\text{Gr}}}} \right)\frac{1}{a} \\ & \Rightarrow \frac{\partial \psi }{{\partial x}} = \frac{1}{a}\left( {\nu \xi \sqrt[4]{{\text{Gr}}}\frac{\partial f}{{\partial \xi }} + \nu \sqrt[4]{{\text{Gr}}}f} \right) \\ & v = - \frac{1}{a}\nu \sqrt[4]{{\text{Gr}}}\left( {\xi \frac{\partial f}{{\partial \xi }} + f} \right) \\ \end{aligned} $$

(14)

$$ \begin{aligned} & \frac{\partial u}{{\partial x}} = \frac{\partial u}{{\partial f}} \cdot \frac{\partial f}{{\partial x}} \\ & \frac{\partial u}{{\partial f}} = \frac{\partial }{\partial f}\left( {\frac{\partial f}{{\partial \eta }} \cdot \frac{1}{a}\sqrt {{\text{Gr}}} v\xi } \right) = \frac{1}{a}\sqrt {{\text{Gr}}} v\xi \frac{\partial }{\partial \eta } \\ & \frac{\partial f}{{\partial x}} = \frac{\partial f}{{\partial \xi }} \cdot \frac{\partial \xi }{{\partial x}} = \frac{\partial f}{{\partial \xi }} \cdot \frac{1}{a} \\ & \frac{\partial u}{{\partial x}} = \frac{1}{a}\sqrt {{\text{Gr}}} v\xi \frac{\partial }{\partial \eta }\frac{\partial f}{{\partial \xi }} \cdot \frac{1}{a} \\ & \frac{\partial u}{{\partial x}} = \frac{1}{{a^{2} }}\sqrt {{\text{Gr}}} v\xi \frac{{\partial f^{\prime}}}{\partial \xi } \\ \end{aligned} $$

(15)

$$ \begin{aligned} & \frac{\partial u}{{\partial y}} = \frac{\partial u}{{\partial f}} \cdot \frac{\partial f}{{\partial y}} \\ & \frac{\partial u}{{\partial f}} = \frac{1}{a}\sqrt {{\text{Gr}}} v\xi \frac{\partial f}{{\partial \eta }} \\ & \frac{\partial f}{{\partial y}} = \frac{\partial f}{{\partial \eta }} \cdot \frac{\partial \eta }{{\partial y}} = f^{\prime}\frac{{\sqrt[4]{{\text{Gr}}}}}{a} \\ & \frac{\partial u}{{\partial y}} = \frac{1}{a}\sqrt {{\text{Gr}}} v\xi \frac{{\partial f^{\prime}}}{\partial \eta }\frac{{\sqrt[4]{{\text{Gr}}}}}{a} \\ & \frac{\partial u}{{\partial y}} = \frac{1}{{a^{2} }}\sqrt {{\text{Gr}}} \sqrt[4]{{\text{Gr}}} v\xi f^{\prime\prime} \\ & \frac{{\partial^{2} u}}{{\partial y^{2} }} = \frac{\partial }{\partial y}\left( {\frac{\partial u}{{\partial y}}} \right) = \frac{\partial }{\partial y}\left( {\frac{1}{{a^{2} }}\sqrt {{\text{Gr}}} \sqrt[4]{{\text{Gr}}} v\xi f^{\prime\prime}} \right) \\ & \frac{{\partial^{2} u}}{{\partial y^{2} }} = \frac{{\text{Gr}}}{{a^{3} }}v\xi f^{\prime\prime\prime} \\ \end{aligned} $$

(16)

$$ \begin{aligned} & \theta \left( {\xi ,\eta } \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }} \Rightarrow T = \theta \left( {T_{w} - T_{\infty } } \right) + T_{\infty } \\ & \frac{\partial T}{{\partial x}} = \frac{\partial T}{{\partial \theta }} \cdot \frac{\partial \theta }{{\partial x}} = \frac{\partial \theta }{{\partial x}}\left( {T_{w} - T_{\infty } } \right) \\ & \frac{\partial \theta }{{\partial x}} = \frac{\partial \theta }{{\partial \xi }} \cdot \frac{\partial \xi }{{\partial x}} = \frac{\partial \theta }{{\partial \xi }} \cdot \frac{1}{a} \\ & \frac{\partial T}{{\partial x}} = \frac{{\left( {T_{w} - T_{\infty } } \right)}}{a}\frac{\partial \theta }{{\partial \xi }} \\ \end{aligned} $$

(17)

$$ \begin{aligned} & \frac{\partial T}{{\partial y}} = \frac{\partial T}{{\partial \theta }} \cdot \frac{\partial \theta }{{\partial y}} = \left( {T_{w} - T_{\infty } } \right)\frac{\partial \theta }{{\partial y}} \\ & \frac{\partial \theta }{{\partial y}} = \frac{\partial \theta }{{\partial \eta }} \cdot \frac{\partial \eta }{{\partial y}} = \frac{{\sqrt[4]{{\text{Gr}}}}}{a} \cdot \frac{\partial \theta }{{\partial \eta }} \\ & \frac{\partial T}{{\partial y}} = \frac{{\left( {T_{w} - T_{\infty } } \right)\sqrt[4]{{\text{Gr}}}}}{a} \frac{\partial \theta }{{\partial \eta }} \\ & \frac{{\partial^{2} T}}{{\partial y^{2} }} = \frac{\partial }{\partial y}\left( {\frac{\partial T}{{\partial y}}} \right) = \frac{\partial }{\partial y}\left( {\frac{{\left( {T_{w} - T_{\infty } } \right)\sqrt[4]{{\text{Gr}}}}}{a} \frac{\partial \theta }{{\partial \eta }}} \right) \\ & \frac{{\partial^{2} T}}{{\partial y^{2} }} = \frac{{\left( {T_{w} - T_{\infty } } \right)\sqrt {{\text{Gr}}} }}{{a^{2} }} \frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} \\ \end{aligned} $$

(18)