Skip to main content
SpringerLink
Log in

Entropy analysis of Powell–Eyring hybrid nanofluid including effect of linear thermal radiation and viscous dissipation

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

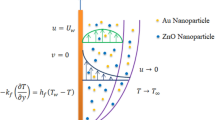
Abstract

Hybrid nanofluids are introduced as heat transfer fluids with greater surface stability, diffusion and dispersion capabilities compared to traditional nanofluids. In this work, flow, convective heat transport and volumetric entropy generation in Powell–Eyring hybrid nanofluid are investigated. Hybrid nanofluid occupies the space over the uniform horizontal porous stretching surface with velocity slip at the interface. Effect of viscous dissipation and linear thermal radiation are also included in the simplified model. Mathematical equations for conservation of mass, momentum, energy and entropy are simplified under assumptions of boundary layer flow of Powell–Eyring hybrid nanofluid. Similarity solutions are obtained by transformation of governing partial differential equations to ordinary differential equations, using similarity variables. Keller box finite difference scheme is then adopted to find the approximate solutions of reduced ordinary differential equations. Numerical computations are performed for alumina–copper water (\({\mathrm{Al}}_2{\mathrm{O}}_3\)–\({\mathrm{Cu/H}}_{2}{\mathrm{O}}\)) hybrid nanofluid and conventional copper water (\({\mathrm{Cu}}\)–\({\mathrm{H}}_{2}{\mathrm{O}}\)) nanofluid. Graphs are produced for velocity, temperature and entropy profiles to study the effect of governing parameters. Skin friction factor and the local Nusselt number are also calculated at the boundary. The notable findings indicate that the hybrid Powell–Eyring nanofluid is better thermal conductor when compared with the conventional nanofluid. The rate of heat transfer at the boundary is greatest for smallest value of the shape factor parameter. The increase in Reynolds number and Brinkman number increases the overall entropy of the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

References

  1. Andersson HI, Aarseth JB, Dandapat BS. Heat transfer in MHD viscoelastic fluid flow over a stretching sheet with variable thermal conductivity, non-uniform heat source and radiation. Int J Heat Mass Transf. 2000;43:69–74.

    Google Scholar 

  2. Cortell R. A note on flow and heat transfer of a viscoelastic fluid over a stretching sheet. Int J Non-Linear Mech. 2006;41:78–85.

    Google Scholar 

  3. Rasheed A, Anwar MS. Simulations of variable concentration aspects in a fractional nonlinear viscoelastic fluid flow. Commun Nonlinear Sci Numer Simul. 2018;65:216–30.

    Google Scholar 

  4. Rehman TU, Ali HM, Janjua MM, Sajjad U, Yan WM. A critical review on heat transfer augmentation of phase change materials embedded with porous materials/foams. Int J Heat Mass Transf. 2018;135:649–73.

    Google Scholar 

  5. Ghadikolaei SS, Hosseinzadeh KH, Yassari M, Sadeghi H, Ganji DD. Analytical and numerical solution of non-Newtonian second-grade fluid flow on a stretching sheet. Therm Sci Eng Prog. 2018;5:309–16.

    Google Scholar 

  6. Rahmati AR, Akbari OA, Marzban A, Karimi R, Pourfattah F. Simultaneous investigations the effects of non-Newtonian nanofluid flow in different volume fractions of solid nanoparticles with slip and no-slip boundary conditions. Therm Sci Eng Prog. 2018;5:263–77.

    Google Scholar 

  7. Rehman TU, Ali HM, Saieed A, Pao W, Ali M. Copper foam/PCMs based heat sinks: an experimental study for electronic cooling systems. Int J Heat Mass Transf. 2018;127:383–91.

    Google Scholar 

  8. Rasheed A, Anwar MS. Interplay of chemical reacting species in a fractional viscoelastic fluid flow. J Mol Liq. 2019;273:576–88.

    CAS  Google Scholar 

  9. Sajawal M, Rehman TU, Ali HM, Sajjad U, Raza A, Bhatti MS. Experimental thermal performance analysis of finned tube-phase change material based double pass solar air heater. Case Stud Therm Eng. 2019;15:100543–12.

    Google Scholar 

  10. Rehman TU, Ali HM. Thermal performance analysis of metallic foam-based heat sinks embedded with RT-54HC paraffin: an experimental investigation for electronic cooling. J Therm Anal Calorim. 2020;140:979–90.

    CAS  Google Scholar 

  11. Rehman TU, Ali HM. Experimental study on the thermal behavior of RT-35HC paraffin within copper and iron–nickel open cell foams: energy storage for thermal management of electronics. Int J Heat Mass Transf. 2020;146:118852.

    CAS  Google Scholar 

  12. Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. In: ASME International Mechanical Engineering Congress and Exposition, vol 66; 1995. p. 99–105.

  13. Qing J, Bhatti MM, Abbas MA, Rashidi MM, Ali MS. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy. 2016;18:123.

    Google Scholar 

  14. Aziz T, Aziz A, Khalique CM. Exact solutions for stokes flow of a non-Newtonian nanofluid model: a lie similarity approach. Z Naturforschung A. 2016;71:621.

    CAS  Google Scholar 

  15. Tausif MD, Das D, Kundu PK. Presence of different shapes of ZrO2 nanoparticles in the melting heat transfer of a Casson flow. Eur Phys J Plus. 2017;132:425.

    Google Scholar 

  16. Bhatti MM, Abbas T, Rashidi MM, Ali MS, Yang Z. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy. 2017;18:224.

    Google Scholar 

  17. Koriko OK, Animasaun IL, Reddy MG, Sandeep N. Scrutinization of thermal stratification, nonlinear thermal radiation and quartic autocatalytic chemical reaction effects on the flow of three-dimensional Eyring–Powell alumina–water nanofluid. Multidiscip Model Mater Struct. 2018;14:261–83.

    CAS  Google Scholar 

  18. Aziz A, Jamshed W. Unsteady MHD slip flow of non-Newtonian Power-law nanofluid over a moving surface with temperature dependent thermal conductivity. Discrete Contin Dyn Syst Ser S. 2018;11:617–30.

    Google Scholar 

  19. Qayyum S, Hayat T, Alsaedi A. Thermal radiation and heat generation/absorption aspects in third grade magneto-nanofluid over a slendering stretching sheet with Newtonian conditions. Phys B Phys Condens Matter. 2018;537:139–49.

    CAS  Google Scholar 

  20. Justh N, Berke B, Laszlo K. Thermal analysis of the improved Hummers synthesis of graphene oxide. J Therm Anal Calorim. 2018;131:2267.

    CAS  Google Scholar 

  21. Selimefendigil F, Chamkha AJ. Magnetohydrodynamics mixed convection in a power law nanofluid-filled triangular cavity with an opening using Tiwari and Das’ nanofluid model. J Therm Anal Calorim. 2019;135:419.

    CAS  Google Scholar 

  22. Aziz A, Shams M. Entropy generation in MHD Maxwell nanofluid flow with variable thermal conductivity, thermal radiation, slip conditions and heat source. AIP Adv. 2020;10:015038.

    CAS  Google Scholar 

  23. Akram N, Sadri R, Kazi SN. A comprehensive review on nanofluid operated solar flat plate collectors. J Therm Anal Calorim. 2020;139:1309.

    CAS  Google Scholar 

  24. Suresh S, Venkitaraj K, Selvakumar P, Chandrasekar M. Experimental investigation of mixed convection with synthesis of Al2O3–water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surf. 2011;08:41–8.

    Google Scholar 

  25. Devi SSU, Devi SPA. Numerical investigation on three dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heatings. Can J Phys. 2016;94:490–6.

    CAS  Google Scholar 

  26. Devi SPA, Devi SSU. Numerical investigation of hydromagnetic hybrid Cu–Al2O3 water nanofluid flow over a permeable stretching sheet with suction. J Nonlinear Sci Appl. 2016;17:249–57.

    CAS  Google Scholar 

  27. Afrand M, Toghraie D, Ruhani B. Effects of temperature and nanoparticles concentration on rheological behavior of Fe3O4–Ag/EG hybrid nanofluid: an experimental study. Exp Therm Fluid Sci. 2016;77:38–44.

    CAS  Google Scholar 

  28. Hayat T, Nadeem S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 2017;7:2317–24.

    Google Scholar 

  29. Ghadikolaei SS, Yassari M, Hosseinzadeh KH, Ganji DD. Investigation on thermophysical properties of TiO2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017;322:428–38.

    CAS  Google Scholar 

  30. Hussain S, Ahmed SE, Akbar T. Investigation on thermophysical properties of TiO2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Int J Heat Mass Transf. 2017;114:1054–66.

    CAS  Google Scholar 

  31. Mehrali M, Sadeghinezhad E, Akhiani AR, Latibari ST, Metselaar HSC, Kherbeet AS, Mehrali M. Heat transfer and entropy generation analysis of hybrid graphene/Fe3O4 ferro-nanofluid flow under the influence of a magnetic field. Powder Technol. 2017;308:149–57.

    CAS  Google Scholar 

  32. Acharya N, Bag R, Kundu PK. Influence of Hall current on radiative nanofluid flow over a spinning disk: a hybrid approach. Phys E Low Dimens Syst Nanostruct. 2019;111:103–12.

    CAS  Google Scholar 

  33. Anuar NS, Bachok N, Arifin NM, Rosali H, Pop I. Stagnation point flow and heat transfer over an exponentially stretching/shrinking sheet in hybrid nanofluid with slip velocity effect: stability analysis. J Phys Conf Ser. 2019;1366:012002.

    CAS  Google Scholar 

  34. Waini I, Ishak A, Pop I. Hybrid nanofluid flow and heat transfer past a permeable stretching/shrinking surface with a convective boundary condition. J Phys Conf Ser. 2019;1366:012022.

    CAS  Google Scholar 

  35. Waini I, Ishak A, Pop I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int J Heat Mass Transf. 2019;136:288–97.

    CAS  Google Scholar 

  36. Waini I, Ishak A, Pop I. Hybrid nanofluid flow and heat transfer over a nonlinear permeable stretching/shrinking surface. Int J Numer Methods Heat Fluid Flow. 2019;29:3110–27.

    Google Scholar 

  37. Maskeen MM, Zeeshan A, Mehmood O, Hassan M. Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. J Therm Anal Calorim. 2019;138:1127–36.

    CAS  Google Scholar 

  38. Huminic G, Huminic A. The heat transfer performances and entropy generation analysis of hybrid nanofluids in a flattened tube. Int J Heat Mass Transf. 2018;119:813–27.

    CAS  Google Scholar 

  39. Bahiraei M, Mazaheri N. Application of a novel hybrid nanofluid containing grapheme–platinum nanoparticles in a chaotic twisted geometry for utilization in miniature devices: thermal and energy efficiency considerations. Int J Mech Sci. 2018;138:337–49.

    Google Scholar 

  40. Jamshed W, Aziz A. Cattaneo–Christov based study of TiO2–Cu/H2O Casson hybrid nanofluid flow over a stretching surface with entropy generation. Appl Nanosci. 2018;8:01–14.

    Google Scholar 

  41. Aziz A, Jamshed W, Ali Y, Shams M. Heat transfer and entropy analysis of Maxwell hybrid nanofluid including effects of inclined magnetic field, Joule heating and thermal radiation. Discrete Contin Dyn Syst Ser S. 2020;13(10):2667–90.

    Google Scholar 

  42. Tiwari RJ, Das MK. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf. 2007;50:2002–18.

    CAS  Google Scholar 

  43. Powell R, Eyring H. Mechanism for relaxation theory of viscosity. Nature. 1944;154:427–8.

    CAS  Google Scholar 

  44. Hayat T, Imtiaz M, Alsaedi A. Effects of homogeneous-heterogeneous reactions in flow of Powell–Eyring fluid. J Cent South Univ. 2015;22:3211–6.

    CAS  Google Scholar 

  45. Hayat T, Qasim M, Mesloub S. MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int J Numer Methods Fluids. 2011;66:963–75.

    Google Scholar 

  46. Jamshed W, Aziz A. A comparative entropy based analysis of Cu and Fe3O4/methanol Powell–Eyring nanofluid in solar thermal collectors subjected to thermal radiation, variable thermal conductivity and impact of different nanoparticles shape. Results Phys. 2018;9:195–205.

    Google Scholar 

  47. Brewster MQ. Thermal radiative transfer and properties. New York: Wiley; 1992.

    Google Scholar 

  48. Keller HB. A new difference scheme for parabolic problems. In: Hubbard B, editor. Numerical solutions of partial differential equations, vol. 2. New York: Academic Press; 1971. p. 327–50.

    Google Scholar 

  49. Vajravelu K, Prasad K. Keller-box method and its application. Berlin: De Gruyter; 2014.

    Google Scholar 

  50. Mutuku WN. Ethylene glycol (EG)-based nanofluids as a coolant for automotive radiator. Asia Pac J Comput Eng. 2016;3:1.

    Google Scholar 

  51. Reddy JVR, Sugunamma V, Sandeep N. Impact of nonlinear radiation on 3D magnetohydrodynamic flow of methanol and kerosene based ferrofluids with temperature dependent viscosity. J Mol Liq. 2017;236:93–100.

    Google Scholar 

  52. Mahmood A, Jamshed W, Aziz A. Entropy and heat transfer analysis using Cattaneo–Christov heat flux model for a boundary layer flow of Casson nanofluid. Results Phys. 2018;10:640–9.

    Google Scholar 

  53. Alsaedi A, Hayat T, Qayyum S, Yaqoob R. Eyring–Powell nanofluid flow with nonlinear mixed convection: entropy generation minimization. Comput Methods Prog Biomed. 2020;186:105183.

    Google Scholar 

  54. Ishak A, Nazar R, Pop I. Mixed convection on the stagnation point flow towards a vertical, continuously stretching sheet. ASME J Heat Transf. 2007;129:1087–90.

    Google Scholar 

  55. Ishak A, Nazar R, Pop I. Boundary layer flow and heat transfer over an unsteady stretching vertical surface. Meccanica. 2009;44:369–75.

    Google Scholar 

  56. Abolbashari MH, Freidoonimehr N, Nazari F, Rashidi MM. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol. 2014;267:256–67.

    CAS  Google Scholar 

  57. Das S, Chakraborty S, Jana RN, Makinde OD. Entropy analysis of unsteady magneto-nanofluid flow past accelerating stretching sheet with convective boundary condition. Appl Math Mech. 2015;36(2):1593–610.

    Google Scholar 

Download references

Acknowledgements

The authors would like to thank the reviewers for their helpful comments and feedback with a view to improve the manuscript. TA and HMSB also would like to acknowledge the adequate support they have received from King Fahd University of Petroleum and Minerals

Author information

Authors and Affiliations

  1. College of Electrical and Mechanical Engineering, National University of Sciences and Technology, Islamabad, 44000, Pakistan

    Asim Aziz

  2. Department of Mathematics, Capital University of Science and Technology, Islamabad, 44000, Pakistan

    Wasim Jamshed

  3. Department of Mathematics, Dammam Community College, King Fahd University of Petroleum and Minerals, KFUPM Box 5084, Dhahran, 31261, Saudi Arabia

    Taha Aziz

  4. Department of Mechanical Engineering, King Fahd University of Petroleum and Minerals, KFUPM Box 5084, Dhahran, 31261, Saudi Arabia

    Haitham M. S. Bahaidarah

  5. Department of Mathematics, Air University, Islamabad, 44000, Pakistan

    Khalil Ur Rehman

Authors
  1. Asim Aziz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wasim Jamshed
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Taha Aziz
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Haitham M. S. Bahaidarah
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Khalil Ur Rehman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Asim Aziz.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aziz, A., Jamshed, W., Aziz, T. et al. Entropy analysis of Powell–Eyring hybrid nanofluid including effect of linear thermal radiation and viscous dissipation. J Therm Anal Calorim 143, 1331–1343 (2021). https://doi.org/10.1007/s10973-020-10210-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-020-10210-2

Keywords

Search

Navigation