Skip to main content
SpringerLink
Log in

Magnetohydrodynamics mixed convection in a power law nanofluid-filled triangular cavity with an opening using Tiwari and Das’ nanofluid model

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

Abstract

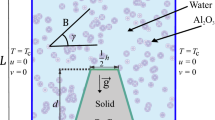
Numerical simulation of mixed convection heat transfer in a lid-driven triangular cavity filled with power law nanofluid and with an opening was performed under the effect of an inclined magnetic field. The left vertical wall of the cavity moves in + y-direction, and the bottom wall of the cavity is partially heated. Galerkin weighted residual finite element method was used to solve the governing equations. Influence of Richardson number, Hartmann number, inclination angle, opening ratio and nanoparticle volume fraction on the fluid flow and heat transfer is examined for various power law indices. It was observed that average heat transfer deteriorates as the value of Richardson number and Hartmann number enhances. At the lowest value of Richardson number, the discrepancy between the average heat transfer corresponding to different power law indices is higher. The inclination angle of the magnetic field where the minimum of the average Nusselt number is seen depends on the fluid type. Average heat transfer number is the highest for the highest value of the opening ratio. The average Nusselt number enhances with solid particle volume fraction, and there are slight variations in the reduction in the average Nusselt number when base fluid and nanofluid are considered for various power law indices.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Abbreviations

\(\mathbf {B}_0\) :

Magnetic field strength

Gr :

Grashof number

h :

Local heat transfer coefficient (\(\hbox {W m}^{-2}\; \hbox {K}^{-1}\))

Ha :

Hartmann number

k :

Thermal conductivity (W \(\hbox {m}^{-1}\; \hbox {K}^{-1}\))

H :

Length of the enclosure (m)

h :

Length of the heater (m)

m :

Consistency coefficient

n :

Power law index

\({Nu}_\mathrm{x}\) :

Local Nusselt number

\({Nu}_\mathrm{m}\) :

Average Nusselt number

p :

Pressure (Pa)

Pr :

Prandtl number

Re :

Reynolds number

Ri :

Richardson number

T :

Temperature (K)

u, v :

x–y velocity components (m \(\hbox {s}^{-1}\))

x, y :

Cartesian coordinates (m)

\(\alpha\) :

Thermal diffusivity (\(\hbox {m}^2\hbox { s}^{-1}\))

\(\beta\) :

Expansion coefficient (\(\hbox {K}^{-1}\))

\(\gamma\) :

Inclination angle (°)

\(\nu\) :

Kinematic viscosity (\(\hbox {m}^2\hbox { s}^{-1}\))

\(\theta\) :

Non-dimensional temperature

\(\rho\) :

Density of the fluid (\(\hbox {kg m}^{-3}\))

\(\sigma\) :

Electrical conductivity (\(\hbox {S m}^{-1}\))

c:

Cold

h:

Hot

m:

Average

References

  1. Varol Y, Koca A, Oztop H. Natural convection in a triangle enclosure with flush mounted heater on the wall. Int. Comm. Heat Mass Transf. 2006;33:951–8.

    Article  Google Scholar 

  2. Yucel N, Turkoglu H. Natural convection in rectangular enclosures with partial heating and cooling. Heat Mass Transf. 1994;29:471–7.

    Google Scholar 

  3. Oztop FH, Estelle P, Yan WM, Al-Salem Khaled, Orfi J, Mahian O. A brief review of natural convection in enclosures under localized heating with and without nanofluids. Int Commun Heat Mass Transf. 2015;60:37–44.

    Article  CAS  Google Scholar 

  4. Oztop HF, Abu-Nada E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int J Heat Fluid Flow. 2008;29:1326–36.

    Article  Google Scholar 

  5. Yucel A. Convection and radiation in a square enclosure. Numer Heat Transfer Part A. 1989;15:261–78.

    Article  Google Scholar 

  6. Selimefendigil F, Oztop HF, Chamkha AJ. MHD mixed convection and entropy generation of nanofluid filled lid driven cavity under the influence of inclined magnetic fields imposed to its upper and lower diagonal triangular domains. J Magn Magn Mater. 2016;406:266–81.

    Article  CAS  Google Scholar 

  7. Selimefendigil F, Oztop HF. Effect of a rotating cylinder in forced convection of ferrofluid over a backward facing step. Int J Heat Mass Transf. 2014;71:142–8.

    Article  Google Scholar 

  8. Banerjee S, Mukhopadhyay A, Sen S, Ganguly R. Thermomagnetic convection in square and shallow enclosures for electronics cooling. Numer Heat Transfer Part A Appl. 2009;55:931–51.

    Article  Google Scholar 

  9. Polat O, Bilgen E. Conjugate heat transfer in inclined open shallow cavities. Int J Heat Mass Transf. 2003;46:1563–73.

    Article  Google Scholar 

  10. Ostrach S. Natural convection heat transfer in cavities and cells. In: Proceedings 7th international heat transfer conference, Toronto, Canada; 1978

  11. Yu P, Qiu J, Qin Q, Tian ZF. Numerical investigation of natural convection in a rectangular cavity under different directions of uniform magnetic field. Int J Heat Mass Transf. 2013;67:1131–44.

    Article  Google Scholar 

  12. Prakash C, Kaminski D. Conjugate natural convection in square enclosure: effect of conduction in one of the vertical walls. HTD ASME. 1984;39:49–54.

    Google Scholar 

  13. Selimefendigil F, Oztop HF, Al-Salem K. Natural convection of ferrofluids in partially heated square enclosures. J Magn Magn Mater. 2014;372:122–33.

    Article  CAS  Google Scholar 

  14. Rahman M, Alim M, Sarker M. Numerical study on the conjugate effect of joule heating and magnato-hydrodynamics mixed convection in an obstructed lid-driven square cavity. Int Commun Heat Mass Transf. 2010;37(37):524–34.

    Article  Google Scholar 

  15. Oztop HF, Al-Salem K, Pop I. MHD mixed convection in a lid-driven cavity with corner heater. Int J Heat Mass Transf. 2011;54:494–3504.

    Google Scholar 

  16. Finlayson B. Convective instability of ferromagnetic fluids. J Fluid Mech. 1970;40:753–67.

    Article  Google Scholar 

  17. Tiwari RK, Das MK. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf. 2007;50:2002–18.

    Article  CAS  Google Scholar 

  18. Armaghani T, Chamkha AJ, Maghrebi M, Nazari M. Numerical analysis of a nanofluid forced convection in a porous channel: a new heat flux model in LTNE condition. J Porous Med. 2014;17:637–46.

    Article  Google Scholar 

  19. Ismael MA, Armaghani T, Chamkha AJ. Conjugate heat transfer and entropy generation in a cavity filled with a nanofluid-saturated porous media and heated by a triangular solid. J Taiwan Inst Chem Eng. 2016;59:138–51.

    Article  CAS  Google Scholar 

  20. Kakac S, Pramuanjaroenkij A. Review of convective heat transfer enhancement with nanofluids. Int J Heat Mass Transf. 2009;52:3187–96.

    Article  CAS  Google Scholar 

  21. Meibodi SS, Kianifar A, Mahian O, Wongwises S. Second law analysis of a nanofluid-based solar collector using experimental data. J Therm Anal Calorim. 2016;126:617–25.

    Article  CAS  Google Scholar 

  22. Rashidi S, Mahian O, Languri EM. Applications of nanofluids in condensing and evaporating systems. J Therm Anal Calorim. 2017; 1–13 (in press)

  23. Mahian O, Kianifar A, Kalogirou SA, Pop I, Wongwises S. A review of the applications of nanofluids in solar energy. Int J Heat Mass Transf. 2013;57:582–94.

    Article  CAS  Google Scholar 

  24. Abu-Nada E, Chamkha AJ. Mixed convection flow in a lid-driven inclined square enclosure filled with a nanofluid. Eur J Mechs B Fluids. 2010;29:472–82.

    Article  Google Scholar 

  25. Armaghani T, Kasaeipoor A, Alavi N, Rashidi M. Numerical investigation of water-alumina nanofluid natural convection heat transfer and entropy generation in a baffled l-shaped cavity. J Mol Liq. 2016;223:243–51.

    Article  CAS  Google Scholar 

  26. Chamkha AJ, Abu-Nada E. Mixed convection flow in single- and double-lid driven square cavities filled with water–Al2O3 nanofluid: Effect of viscosity models. Eur J Mech B Fluids. 2012;36:82–96.

    Article  Google Scholar 

  27. Selimefendigil F, Oztop HF. Identification of forced convection in pulsating flow at a backward facing step with a stationary cylinder subjected to nanofluid. Int Commun Heat Mass Transf. 2013;45:111–21.

    Article  CAS  Google Scholar 

  28. Selimefendigil F, Oztop HF. Mixed convection of nanofluids in a three dimensional cavity with two adiabatic inner rotating cylinders. Int J Heat Mass Transf. 2018;117:331–43.

    Article  CAS  Google Scholar 

  29. Abu-Nada E. Application of nanofluids for heat transfer enhancement of separated flows encountered in a backward facing step. Int J Heat Fluid Flow. 2008;29:242–9.

    Article  CAS  Google Scholar 

  30. Shenoy A, Sheremet M, Pop I. Convective flow and heat transfer from wavy surfaces: viscous fluids. Porous media and nanofluids. Boca Raton: CRC Press, Taylor and Francis Group; 2016.

    Book  Google Scholar 

  31. Das SK, Choi SUS, Yu W, Pradeep Y. Nanofluids: science and technology. Hoboken: Wiley; 2008.

    Google Scholar 

  32. Grosan T, Sheremet MA, Pop I. In: Heat transfer enhancement in cavities filled with nanofluids. 2017; 267–284

  33. Bahiraei M. A numerical study of heat transfer characteristics of Cuo–water nanofluid by euler–lagrange approach. J Therm Anal Calorim. 2016;123:1591–9.

    Article  CAS  Google Scholar 

  34. Selimefendigil F, Oztop HF. Modeling and optimization of MHD mixed convection in a lid-driven trapezoidal cavity filled with alumina–water nanofluid: effects of electrical conductivity models. Int J Mech Sci. 2018;136:264–78.

    Article  Google Scholar 

  35. Sheikholeslami M, Bandpy MG, Ganji D. Numerical investigation of MHD effects on Al2o3–water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM. Energy. 2013;60:501–10.

    Article  CAS  Google Scholar 

  36. Selimefendigil F, Oztop HF. Numerical study of MHD mixed convection in a nanofluid filled lid driven square enclosure with a rotating cylinder. Int J Heat Mass Transf. 2014;78:741–54.

    Article  Google Scholar 

  37. Sheikholeslami M, Bandpy MG, Ellahi R, Zeeshan A. Simulation of MHD Cuo–water nanofluid flow and convective heat transfer considering lorentz forces. J Magn Magn Mater. 2014;369:69–80.

    Article  CAS  Google Scholar 

  38. Selimefendigil F, Oztop HF. Conjugate natural convection in a nanofluid filled partitioned horizontal annulus formed by two isothermal cylinder surfaces under magnetic field. Int J Heat Mass Transf. 2017;108:156–71.

    Article  CAS  Google Scholar 

  39. Hatami M, Sheikholeslami M, Hosseini M, Ganji DD. Analytical investigation of MHD nanofluid flow in non-parallel walls. J Mol Liq. 2014;194:251–9.

    Article  CAS  Google Scholar 

  40. Chamkha AJ, Rashad AM, Mansour MA, Armaghani T, Ghalambaz M. Effects of heat sink and source and entropy generation on MHD mixed convection of a cu-water nanofluid in a lid-driven square porous enclosure with partial slip. Phys Fluids. 2017;29:052001.

    Article  CAS  Google Scholar 

  41. Chamkha AJ, Rashad AM, Armaghani T, Mansour MA. Effects of partial slip on entropy generation and MHD combined convection in a lid-driven porous enclosure saturated with a cu-water nanofluid. Journal of Thermal Analysis and Calorimetry. 2017 (in press)

  42. Selimefendigil F, Oztop HF. MHD mixed convection of nanofluid filled partially heated triangular enclosure with a rotating adiabatic cylinder. J Taiwan Inst Chem Eng. 2014;45:2150–62.

    Article  CAS  Google Scholar 

  43. Mahmoudi A, Mejri I, Abbassi MA, Omri A. Lattice boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with linear temperature distribution. Powder Technol. 2014;256:257–71.

    Article  CAS  Google Scholar 

  44. Sheikholeslami M, Abelman S. Two-phase simulation of nanofluid flow and heat transfer in an annulus in the presence of an axial magnetic field. IEEE Trans Nanotechnol. 2015;14:561–9.

    Article  CAS  Google Scholar 

  45. Rashad A, Armaghani T, Chamkha A, Mansour M. Entropy generation and MHD natural convection of a nanofluid in an inclined square porous cavity: effects of a heat sink and source size and location. Chin J Phys. 2018;56:193–211.

    Article  CAS  Google Scholar 

  46. Selimefendigil F, Oztop HF. Influence of inclination angle of magnetic field on mixed convection of nanofluid flow over a backward facing step and entropy generation. Adv Powder Technol. 2015;26:1663–75.

    Article  CAS  Google Scholar 

  47. Sheikholeslami M, Rashidi M, Ganji D. Effect of non-uniform magnetic field on forced convection heat transfer of image-water nanofluid. Comput Methods Appl Mech Eng. 2015;294:299–312.

    Article  Google Scholar 

  48. Selimefendigil F, Chamkha AJ. Natural convection of a hybrid nanofluid-filled triangular annulus with an opening. Comput Thermal Sci. 2016;8:555–66.

    Article  Google Scholar 

  49. Muftuoglu A, Bilgen E. Natural convection in an open square cavity with discrete heaters at their optimized positions. Int J Therm Sci. 2008;47:369–77.

    Article  CAS  Google Scholar 

  50. Hsu TH, Hong KY. Natural convection of micropolar fluids in an open cavity. Numer Heat Transf Part A. 2006;50:281–300.

    Article  Google Scholar 

  51. Bilgen E, Muftuoglu A. Natural convection in an open square cavity with slots. Int Commun Heat Mass Transf. 2008;35:896–900.

    Article  CAS  Google Scholar 

  52. Kefayati G. Simulation of magnetic field effect on natural convection of non-newtonian power-law fluids in a sinusoidal heated cavity using FDLBM. Int Commun Heat Mass Transf. 2014;53:139–53.

    Article  Google Scholar 

  53. Kefayati G. FDLBM simulation of magnetic field effect on non-newtonian blood flow in a cavity driven by the motion of two facing lids. Powder Technol. 2014;253:325–37.

    Article  CAS  Google Scholar 

  54. Mendu SS, Das P. Flow of power-law fluids in a cavity driven by the motion of two facing lids—a simulation by lattice boltzmann method. J Non Newton Fluid Mech. 2012;175:10–24.

    Article  CAS  Google Scholar 

  55. Polat O, Bilgen E. Laminar natural convection in shallow open cavities. Int J Therm Sci. 2002;41:360–8.

    Article  Google Scholar 

  56. Maxwell J. A treatise on electricity and magnetism. Oxford: Oxford University Press; 1873.

    Google Scholar 

  57. Brinkman H. The viscosity of concentrated suspensions and solutions. J Chem Phys. 1952;20:571–81.

    Article  CAS  Google Scholar 

  58. Pirmohammadi M, Ghassemi M. Effect of magnetic field on convection heat transfer inside a tilted square enclosure. Int Commun Heat Mass Transf. 2009;36:776–80.

    Article  CAS  Google Scholar 

  59. Sarris I, Zikos G, Grecos A, Vlachos N. On the limits of validity of the low magnetic reynolds number approximation in MHD natural-convection heat transfer. Numer Heat Transf Part B. 2006;50:158–80.

    Article  CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Celal Bayar University, 45140, Manisa, Turkey

    Fatih Selimefendigil

  2. Mechanical Engineering Department, Prince Sultan Endowment for Energy and Environment, Prince Mohammad Bin Fahd University, Al-Khobar, 31952, Saudi Arabia

    Ali J. Chamkha

  3. RAK Research and Innovation Center, American University of Ras Al Khaimah, Ras Al Khaimah, United Arab Emirates

    Ali J. Chamkha

Authors
  1. Fatih Selimefendigil
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ali J. Chamkha
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ali J. Chamkha.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Selimefendigil, F., Chamkha, A.J. Magnetohydrodynamics mixed convection in a power law nanofluid-filled triangular cavity with an opening using Tiwari and Das’ nanofluid model. J Therm Anal Calorim 135, 419–436 (2019). https://doi.org/10.1007/s10973-018-7037-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-018-7037-x

Keywords

Search

Navigation