Abstract
The gadolinium ferrochromite (GdFe1−xCrxO3) was used as a case study of influence of chromium substitution on the perovskite structure in the entire composition range. By exploiting thermal analysis techniques (dilatometry, differential thermal analysis) the influence of chromium was investigated in the context of thermal stability of the canted antiferromagnetic ordering. It was found that the higher the chromium concentration was, the more the Néel temperature decreased, e.g., substitution of 26 % of iron atoms corresponded to a depression of about 60 K with respect to undoped gadolinium ferrite. For higher chromium concentrations the mixed gadolinium ferrochromite was paramagnetic at room temperature. Additional information on the crystal structure and, qualitatively, on the magnetic ordering as well was derived from the results of X-ray diffraction and Mössbauer spectroscopy measurements. For chromium content higher than 10 % the gadolinium ferrochromite may be regarded as a solid solution. For lower concentrations, however, a possible formation of clusters with different Fe/Cr ratio occurs as suggested by Mössbauer spectra.
Similar content being viewed by others
Introduction
Lanthanide-transition metal mixed oxides emerged in recent years as potential catalysts [1–3], sensors [4–7] and materials for harvesting of solar energy [8, 9]. Two of those examples are the families of lanthanide orthoferrites (LnFeO3, where Ln represents a lanthanide trivalent ion) and lanthanide orthochromites (LnCrO3), who may serve as visible light absorbers due to an optical absorption edge situated around 1–2.8 eV [10–13].
Both families of compounds show structural similarities, i.e., they crystallize in Pbnm orthorhombic space group with a distorted perovskite structure [14, 15], and show canted antiferromagnetic spin ordering. When compared, the edges of the MeO6 octahedra differ by 2 % only, with the difference between Fe+3 and Cr+3 ions less than 5 % [16], But in spite of being structurally similar their magnetic properties are in significant contrast. Even though they both melt congruently [17], [18] after [19], their melting points differ by 600 K, i.e., ca. 2070 K for GdFeO3 and ca. 2670 K for GdCrO3. One also finds that the Néel transition temperature (TN) is usually higher for orthoferrites than for the orthochromites, e.g., TN = 657 K for GdFeO3 [20, 21] but TN = 167 K for GdCrO3 [22]. This means the former compounds possess an effective magnetic momentum at room temperature, whereas the latter do not. The internal magnetic field is disadvantageous for electrical carrier propagation, generating losses in the electrical flux, e.g., the antiparallel magnetic domain ordering in the rare earth manganites, which leads to the colossal magnetoresistance [23]. It is therefore important to pinpoint that composition range, in which the paramagnetic ordering would be preferential at room temperature. Some attempts of material modification were already made in the case of substitution of rare earth ions [24–26] or transition metal cations [27–30]. As a result the magnetic ordering is destroyed, and when the substituting ion has a different valency the resistivity decreases as well due to the increase in concentration of free charge carriers.
This study aims at finding the potential applicability range of gadolinium ferrochromite—GdFe1−xCrxO3 (GFCO) with respect to magnetic ordering studied by dilatometry and differential thermal analysis backed up with structural data on crystal symmetry (X-ray diffraction) and Fe+3 positioning (Mössbauer spectroscopy).
Experimental
Preparation
The ferrochromite powders were prepared by modified combustion method [31, 32]. High-purity oxide materials (Gd2O3—99.99 % Alfa Aesar®, Fe2O3—99.99 % RIC-ROC™, Cr2O3—99.999 % Alfa Aesar®) were used. First, the Fe+3/Cr+3 stock was prepared by dissolving Fe2O3 and Cr2O3 oxides in boiling deionized water with minor addition of HCl to enhance the process. Then, HNO3 was added in amount sufficient to enable the formation of stoichiometric nitrates and Gd2O3 was dissolved. Finally, when stocks were optically transparent, glycine was added in molar ratio 1.15:1 with respect to the calculated molar concentration of nitrates, forming a homogenous viscous solution. Further reduction of the stock resulted in formation of gel, which autoignited, forming a fluffy, voluminous ash. Thus, obtained powders were preheated in 1050 °C in air for 3 h and then grounded in alumina mortar.
For dilatometric measurements the powders were isostatically pressed in the 25 × 15 × 5 mm rectangular form and sintered at 1500 °C for 12 h. Then 5 × 5 × 25 mm samples were cut and polished from both sides until front and rear surfaces were perpendicular to the length axis.
X-ray diffraction (XRD)
Phase analysis and structural refinement of the powdered samples were performed by X-ray powder diffraction using Cu Kα1,2 radiation (U = 40 kV, I = 30 mA) with a Siemens D500 diffractometer equipped with a semiconductor, high-resolution detector Si:Li. Data were collected in the 2θ angle range 20° < 2θ < 90° with a step of 0.02° and counting time of 5 s/step. The powder diffraction patterns were analyzed by the Rietveld refinement method using PowderCell v.2.4 program and database ICDD PDF4+2014. All the main reflections were well indexed to a orthorhombic cell in the space group Pbnm (62) with occupation Wyckoff’s 4b site by mixed Cr and Fe cations. There were no other visible phases on measured diffraction patterns.
Mössbauer spectroscopy
The samples were used in the Mössbauer measurements as absorbers and measured at 300 K in the transmission geometry using a conventional constant acceleration spectrometer. The 57Co in Rh source with the activity of about 50 mCi was used. The isomer shifts were related to the α-Fe standard.
Differential thermal analysis (DTA)
Powder samples were measured in differential thermal analysis (DTA) configuration using STA 449 F1 Jupiter® (NETZSCH). A standard platinum crucible was filled with 500 mg of powder and measured up to 400 °C in synthetic air (Ar—60 mL min−1, O2—15 mL min−1) with a heating rate of 2 K min−1 and a cooling rate of 10 K min−1. When lower mass samples, e.g., 200, 300 mg were used, the phase transition signal was not clearly visible for all samples. Each run was repeated twice.
Dilatometry
The dilation curves were recorded using DIL 402 PC (NETZSCH) from room temperature to 1500 °C with heating rate of 2 K min−1 in static air. A 25-mm sapphire was used as a standard.
Results and discussion
Crystallinity and phase purity
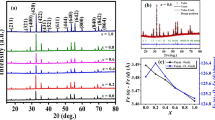
All synthesized compounds crystallized in an orthorhombic crystal system characteristic for GdFeO3, namely Pbnm space group with distorted perovskite structure, as deduced from analysis of X-ray diffractograms (Fig. 1). The merging of peaks positioned around 70° suggested that the expansion of the crystal lattice is non-uniform for all main directions. This can be seen as a non-monotonic change of the distortion angle—arctan(b/a) with respect to chromium content (Fig. 3). Even though the volume changed significantly, the a-b plane deformation of the primary cell of near end compounds was very small. Substitution of iron with chromium resulted in a decrease in cell constant values (Fig. 2), which is to be expected from difference in ionic radii—0.645Å for Fe+3 against 0.615Å for Cr+3 (as given by Shannon and Prewitt [16]). The cell contraction phenomenon was not uniform for all main crystallographic directions, as could be judged from Table 1 and Fig. 2. The volumetric contraction was, though, as was deduced from approximately linear character of the plot with respect to the chromium content (Fig. 3). Another information about the crystal structure at room temperature came from the distortion angle (Table 1), equal to 90° for primary cubic perovskite. The distortion angle can be thought of as a quantitative descriptor of the structural deformation in the a-b plane of the orthorhombic structure. Substitution of iron by chromium leads to its decrease, except for the ferrochromites with chemical composition close to the pure substances, where the angle took values roughly the same as the undoped compounds—87.32° for GdFeO3 and GdFe0.8953Cr0.1047O3, 87.75° for GdFe0.25Cr0.75O3 and GdCrO3. One finds that the c/a and c/b ratios decrease as well, when the concentration of chromium increases.
Reduced lattice constants of the GFCO perovskites. The a’ and b’ correspond to a/√2 and b/√2, respectively, whereas c’ = c/2. The reduction was utilized to transform present crystal lattices into that of a primary cubic perovskite. Due to a large dissimilarity between lattice constant values, the system can be considered as strongly distorted
Volume contraction and distortion angle plotted against chromium content. The linear appearance of the volume versus composition plot suggests a solid solution character of the GFCO compounds. The increase in distortion angle corresponds to the lower distortion of the reduced GFCO cell with respect to the ideal cubic symmetry. The plateau character of the distortion angle for near end members suggests the low degree of lattice deformation in the x–y plane
Thermal analysis
Thermal expansion coefficient (TEC)
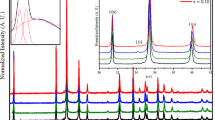
The GdFeO3 perovskite exhibits only one phase transition above room temperature, namely the order–disorder Néel transition at 657 K [6] [7]. At room temperature GdFeO3 is a weak ferromagnet, due to Dzyaloshinskii–Moriya interaction, which tilts the FeO6 octahedra and leads to formation of an effective magnetic momentum. At Néel temperature the FeO6 octahedra rotate (the process is accompanied by a small increase in volume) leaving a trace on the thermal expansion curve. For the undoped gadolinium ferrite, the peak value of the TEC was ca. 640 K. Looking at the TEC plots (Fig. 4) we saw that the phase transition does not change its temperature position for x = 0.1047 and shifts by around −60 K for x = 0.2598. In the latter case, the peak is much broader, which we attribute to the inhomogeneity in cation distribution and thermal inertia of the experimental setup. It was not possible, however, to pinpoint the leading cause of the broadening. Substitution of 51 % (or more) iron atoms with chromium shifted the transition temperature below the technical detection range, i.e., about 380 K. Should the Néel transition temperature be taken as the peak value of the thermal expansion coefficient, they would be as follows: 626 K (GdFeO3), 633 K (GdFe0.8953Cr0.1047O3), 561 K (GdFe0.7402Cr0.2598O3). This trend is similar to the one reported by Widatallah et al. [28] who observed the disappearance of room-temperature weak ferromagnetism in EuCr1−xFexO3 nanoparticles around x = 0.5.
Thermal expansion coefficient curves of GFCO perovskites. The order–disorder phase transition is seen as a delta-shaped peak, gradually shifting from 640 K to lower temperatures as the chromium content increases. The broad character of the peak for x = 0.2598 is thought to arise simultaneously from the instrumental broadening and the inhomogenous distribution of the Fe/Cr cations
Differential thermal analysis
No visible signal change was recorded during heating (Fig. 5), which was thought to be caused by dissipation of heat on the dispersed powder. A significant change in the slope of the DTA signal is seen during cooling (cooling rate of 10 K min−1). Since the break for GdFeO3 (x = 0) occurs at roughly the same temperature as the Néel transition reported by Parida et al. [21] (651 vs 657 K), it was deduced that the similar breaks in the DTA signal corresponded to the Néel transition itself. The estimated Néel temperatures were: 651 K (GdFeO3), 562 K (GdFe0.7402Cr0.2598O3). No clear signal change was observed for the GdFe0.8953Cr0.1047O3 compound.
DTA signal recorded for ferrochromite powder samples with chromium content up to 26 %. The open symbols indicate the heating run (heating rate 2 K min−1)—no visible change in DTA signal is seen from room temperature up to 780 K. During cooling (cooling rate 10 K min−1) signal breaks are observed for x = 0 (solid line) and x = 0.2598 (dash line). No clear change in DTA signal is observed for x = 0.1047 (dot line)
Mössbauer spectroscopy
A good agreement of the Mössbauer parameters for undoped GdFeO3 was found between the current results and those reported by Eibschütz et al. [20] and Romero et al. [33]. Only one magnetic sextet with sharp lines was observed. The hyperfine field of about 50T was estimated from Mössbauer spectra (Fig. 6a—GFO). When chromium ions were introduced into the crystal lattice formation of additional magnetic sextets was observed. Consequently, additional sets of fitting parameters (isomeric shift, quadrupole splitting and hyperfine field) could be computed (Table 2). The presence of 10.47 at% Cr+3 in Gd(Fe, Cr)O3 compound resulted in the formation of three sextets (Fig. 6b). In the case of 25.98 at% Cr+3 the absorption peaks were very broad and irregular—for that reason the hyperfine field distribution (Fig. 7) was extracted from the spectrum (Fig. 6c). A broad maximum positioned at about 44T was found, suggesting that 57Fe surrounding was not well defined in the present system. On the contrary, there seemed to be a great variety of positions differing very little from one to another in the values of the hyperfine field. When x ≥ 0.5129, the samples of Gd(Fe, Cr)O3 were non-magnetic at room temperature and only the quadrupole splitting was observed (Fig. 6d, e).
Hyperfine field probability distribution calculated for the GFCO compound (Fig. 6) with x = 0.2598 denoted with open circles (the lines are only to guide the eye). The broad maximum positioned around 44T is the result of a superposition of 57Fe states varying very little one from another and can be regarded as a trace of the solid solution. The non-symmetric character of the bell curve suggests that the occupancy of the Wyckoff’s 4b site by Cr+3 and Fe+3 may not necessarily be equiprobable
A possible explanation of the spectrum broadening was the formation of clusters with different Cr+3/Fe+3 ratios. Since the content exceeding 51 at% of Cr+3 destroys the magnetic ordering, the clusters are formed with excess of Fe+3 ions over Cr+3 ions. Thus, in the case of x ≈ 0.10, there are three clusters with different Cr+3/Fe+3 ratios and a large number of them (or a homogenous distribution) for x ≈ 0.26. It is worth noting that for x ≈ 0.10 one of the 57Fe positions has similar parameters to that of an undoped GdFeO3 and thus may correspond to a cluster with marginal admixture of chromium. One must be aware though that the natural abundance of 57Fe is 2.19 % and so only 1 per 50 atomic positions of Fe+3 are scouted out.
Conclusions
Gadolinium ferrochromites were synthesized by modified glycine-nitrate combustion method in the form of powders. Judging from the TEC and DTA curves, substitution of iron with chromium gradually decreases the Néel temperature (651 K for GdFeO3 to 562 K for GdFe0.7402Cr0.2598O3) and for 51 % Cr it is no longer observed. The transition temperatures estimated from the DTA curves are in very good agreement with the literature reports for the GdFeO3 but exhibit even 25 K difference with respect to the values estimated from the TEC curves. The temperatures estimated from the TEC curve seem less accurate due to significantly lower signal-to-noise ratio and should be taken with caution.
All synthesized compounds crystallize in Pbnm space group, and it was observed that introduction of chromium to the crystal lattice reduces the orthorhombic distortion with respect to the ideal cubic perovskite (the c/a and c/b ratios are simultaneously reduced when chromium concentration was increased). Although the X-ray diffractograms suggest all ferrochromites behave like solid solutions, basing the Mössbauer spectroscopy results it is proposed that the clusters with differing Cr+3/Fe+3 ratio such that 0 ≤ Cr+3/Fe+3 < 1.04 are formed. Introduction of chromium into the GdFeO3 crystal structure weakens the canted antiferromagnetic ordering (x < 0.51) and destroys it when Cr+3/Fe+3 exceeds 1.04 (x ≈ 0.51).
Further attention should be payed to the study of optical absorption and electrical conductivity of ferrochromite compounds before any definite conclusions are made on the choice of composition range of the most benefit for the harvesting of solar energy.
References
Kuhn J, Ozkan U. Surface properties of Sr- and Co-doped LaFeO3. J Catal. 2008;253:200–11. doi:10.1016/j.jcat.2007.10.005.
Ji K, Dai H, Deng J, Jiang H, Zhang L, Zhang H, Cao Y. Catalytic removal of toluene over three-dimensionally ordered macroporous Eu1–xSrxFeO3. Chem Eng J. 2013;214:262–71. doi:10.1016/j.cej.2012.10.083.
Zhao K, He F, Huang Z, Zheng A, Li H. Three-dimensionally ordered macroporous LaFeO3 perovskites for chemical-looping steam reforming of methane. Int J Hydrogen Energy. 2013;39:3243–52. doi:10.1016/j.ijhydene.2013.12.046.
Tsang SC, Bulpitt C. Rare earth oxide sensors for ethanol analysis. Sensors Actuators B Chem. 1998;52:226–35.
Ahmed MA, El-Dek SI. Optimizing the physical characterizations of orthoferrites to be used as pressure and gamma sensor. Mater Lett. 2006;60:1437–46. doi:10.1016/j.matlet.2005.11.076.
Hosoya Y, Itagaki Y, Aono H, Sadaoka Y. Ozone detection in air using SmFeO3 gas sensor. Sens Actuators B Chem. 2005;108:198–201. doi:10.1016/j.snb.2004.10.059.
Siemons M, Simon U. High throughput screening of the propylene and ethanol sensing properties of rare-earth orthoferrites and orthochromites. Sens Actuators B Chem. 2007;126:181–6. doi:10.1016/j.snb.2006.11.022.
Evdou A, Zaspalis V, Nalbandian L. La1−xSrxFeO3−δ perovskites as redox materials for application in a membrane reactor for simultaneous production of pure hydrogen and synthesis gas. Fuel. 2010;89:1265–73. doi:10.1016/j.fuel.2009.09.028.
Natali Sora I, Fontana F, Passalacqua R, Ampelli C, Perathoner S, Centi G, Parrino F, Palmisano L. Photoelectrochemical properties of doped lanthanum orthoferrites. Electrochim Acta. 2013;109:710–5. doi:10.1016/j.electacta.2013.07.132.
Wood DL. Optical Spectra of Rare-Earth Orthoferrites. J Appl Phys. 1970;41:5315. doi:10.1063/1.1658669.
Jaiswal A, Das R, Adyanthaya S, Poddar P. Synthesis and optical studies of GdCrO3 nanoparticles. J Nanopart Res. 2010;13:1019–27. doi:10.1007/s11051-010-0090-4.
Zhu LP, Deng HM, Sun L, Yang J, Yang PX, Chu JH. Optical properties of multiferroic LuFeO3 ceramics. Ceram Int. 2014;40:1171–5. doi:10.1016/j.ceramint.2013.07.001.
Bellakki MB, Kelly BJ, Manivannan V. Synthesis, characterization, and property studies of (La, Ag) FeO3 (0.0 ≤ x ≤ 0.3) perovskites. J Alloys Compd. 2010;489:64–71. doi:10.1016/j.jallcom.2009.08.059.
Geller S. Crystal Structure of Gadolinium Orthoferrite, GdFeO3. J. Chem. Phys. 1956;24:1236–9. doi:10.1063/1.1742746.
Zaitseva ZA, Litvin AL. Specification of crystal structure of neodymium and gadolinium chromite, Dop Ak Nauk Ukr RSR Ser B-Geol Khim. Biol Nauk (1978) 994–997.
Shannon RD, Prewitt CT. Effective ionic radii in oxides and fluorides. Acta Crystallogr B. 1969;25:925–46. doi:10.1107/s0567740869003220.
Warshaw I, Roy R. Stable and Metastable Equilibria in the Systems Y2O2-Al2O3, and Gd2O3-Fe2O3. J Am Ceram Soc. 1959;42:434–8. doi:10.1111/j.1151-2916.1959.tb12970.x.
Phase Equilibria Diagrams Database 3.0, (n.d.).
Berjoan R. Ph. D. Dissertation, Odeillo/Font-Romeu, France, 1975.
Eibschütz M, Shtrikman S, Treves D. Mössbauer studies of Fe57 in orthoferrites. Phys Rev. 1967;156:562–77.
Parida SC, Rakshit SK, Singh Z. Heat capacities, order-disorder transitions, and thermodynamic properties of rare-earth orthoferrites and rare-earth iron garnets. J Solid State Chem. 2008;181:101–21.
Jaiswal A, Das R, Vivekanand K, Maity T, Abraham PM, Adyanthaya S. Magnetic and dielectric properties and Raman spectroscopy of GdCrO3 nanoparticles. J Appl Phys. 2010;. doi:10.1063/1.3275926.
Pickett W, Singh D. Electronic structure and half-metallic transport in the La1−xCaxMnO3 system. Phys Rev B. 1996;53:1146–60. doi:10.1103/PhysRevB.53.1146.
Acharya S, Deb AK, Das D, Chakrabarti PK. Enhanced magnetic behavior of Al substituted LaFeO3 (La(1−x)AlxFeO3, x = 0.10 and 0.30). Mater Lett. 2011;65:1280–2. doi:10.1016/j.matlet.2011.01.049.
Hung M-H, Rao MVM, Tsai D-S. Microstructures and electrical properties of calcium substituted LaFeO3 as SOFC cathode. Mater Chem Phys. 2007;101:297–302. doi:10.1016/j.matchemphys.2006.05.008.
Ahmad I, Akhtar MJ, Siddique M, Iqbal M, Hasan MM. Origin of anomalous octahedral distortions and collapse of magnetic ordering in Nd1−xSrxFeO3 (0 ≤ x ≤ 0.5). Ceram Int. 2013;39:8901–9. doi:10.1016/j.ceramint.2013.04.084.
Shah J, Kotnala RK. Room temperature magnetoelectric coupling enhancement in Mg-substituted polycrystalline GdFeO3. Scr Mater. 2012;67:316–9. doi:10.1016/j.scriptamat.2012.05.003.
Widatallah HM, Al-Shahumi TM, Klencsár Z, Pekala M, Gismelseed AM, Al-Omari IA, Al-Rawas AD, Seifu D. Structural, magnetic and 151Eu Mössbauer studies of mechanosynthesized nanocrystalline EuCr1−xFexO3 particles. Acta Mater. 2013;61:4461–73. doi:10.1016/j.actamat.2013.04.015.
Bashir A, Ikram M, Kumar R, Lisboa-Filho PN, Thakur P. Structural, electronic structure and magnetic studies of SmFe1−xNixO3 (x ≤ 0.5). Mater Sci Eng, B. 2010;172:242–7. doi:10.1016/j.mseb.2010.05.024.
Bashir A, Ikram M, Kumar R, Lisboa-Filho PN. Structural, electronic structure and magnetic studies of GdFe1−xNixO3 (x ≤ 0.5). J Alloys Compd. 2012;521:183–8. doi:10.1016/j.jallcom.2012.01.121.
Bedekar V, Jayakumar OD, Manjanna J, Tyagi AK. Synthesis and magnetic studies of nano-crystalline GdFeO3. Mater Lett. 2008;62:3793–5. doi:10.1016/j.matlet.2008.04.053.
Kondakindi RR, Karan K, Peppley BA. A simple and efficient preparation of LaFeO3 nanopowders by glycine–nitrate process: Effect of glycine concentration. Ceram Int. 2012;38:449–56. doi:10.1016/j.ceramint.2011.07.026.
Romero M, Gómez RW, Marquina V, Pérez-Mazariego JL, Escamilla R. Synthesis by molten salt method of the AFeO3 system (A = La, Gd) and its structural, vibrational and internal hyperfine magnetic field characterization. Phys B Condens Matter. 2014;443:90–4. doi:10.1016/j.physb.2014.03.024.
Acknowledgements
The authors thank the HARMONIA Project (2013/10/M/ST5/00650) from the National Science Centre.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Orlinski, K., Diduszko, R., Kopcewicz, M. et al. The influence of chromium substitution on crystal structure and shift of Néel transition in GdFe1−xCrxO3 mixed oxides. J Therm Anal Calorim 127, 181–187 (2017). https://doi.org/10.1007/s10973-016-5879-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10973-016-5879-7