Skip to main content
SpringerLink
Log in

A Faber–Krahn Inequality for Indented and Cut Membranes

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

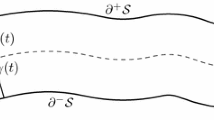
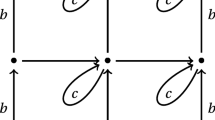
In 1960, Payne and Weinberger proved that, among all domains that lie within a wedge (an angle whose measure is less than or equal to π) and have a given value of a certain integral, the circular sector has the lowest fundamental eigenvalue of the Dirichlet Laplacian. We show that an analogue of this assertion is true for domains with a cut and for indented domains, i.e., for those located in a reflex angle (its measure is between π and 2π).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. W. S. Rayleigh, The Theory of Sound, Dover, New York (1945).

    MATH  Google Scholar 

  2. J. R. Kuttler and V. G. Sigillito, “Eigenvalues of the Laplacian in two dimensions,” SIAM Rev. 26, 163–193 (1984).

    Article  MathSciNet  MATH  Google Scholar 

  3. M. S. Ashbaugh and R. D. Benguria, “Isoperimetric Inequalities for Eigenvalues of the Laplacian,” Proc. Symp. Pure Math. 76, Pt. 1, 105–139 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  4. C. Bandle, Isoperimetric Inequalities and Applications, Pitman, Boston etc. (1980).

    MATH  Google Scholar 

  5. M. Abramowitz (Ed.) and I. A. Stegun (Ed.), Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, U.S. Department of Commerce, Washington (1964).

  6. G. Faber, “Beweis, dass unter allen homogenen Membranen von gleicher Fläche und gleicher Spannung die kreisförmige den tiefsten Grundton gibt” [in German], Münch. Ber. 1923, 169–172 (1923).

    MATH  Google Scholar 

  7. E. Krahn, “Über eine von Rayleigh formulierte Minimaleigenschaft des Kreises” [in German], Math. Ann. 94, 97–100 (1925).

    Article  MathSciNet  MATH  Google Scholar 

  8. E. Krahn, “Über Minimaleigenschaften der Kugel in drei und mehr Dimensionen” [in German], Acta Univ. Dorpat A9, 1–44 (1926).

    MATH  Google Scholar 

  9. L. E. Payne and H. F. Weinberger, “A Faber–Krahn inequality for wedge-like membranes,” J. Math. Physics 39, 182–188 (1960).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory for Mathematical Modelling of Wave Phenomena, Institute for Problems in Mechanical Engineering, RAS, V.O., Bol’shoy pr. 61, St Petersburg, 199178, Russia

    N. Kuznetsov

Authors
  1. N. Kuznetsov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. Kuznetsov.

Additional information

Translated from Problemy Matematicheskogo Analiza 125, 2023, pp. 105-109.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kuznetsov, N. A Faber–Krahn Inequality for Indented and Cut Membranes. J Math Sci 276, 111–116 (2023). https://doi.org/10.1007/s10958-023-06728-z

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-023-06728-z

Search

Navigation