Skip to main content
SpringerLink
Log in

Five-Vertex Model and Lozenge Tilings of a Hexagon with a Dent

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

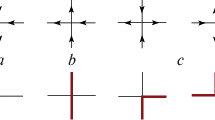
We consider the five-vertex model on a regular square lattice of the size L × M with boundary conditions fixed in such a way that configurations of the model are in one-to-one correspondence with the lozenge tilings of the hexagon with a dent. We obtain two determinant representations for the partition function. In the free-fermionic limit, this result implies some summation formulae for Schur functions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. W. Kasteleyn, “The statistics of dimers on a lattice: I. The number of dimer arrangements on a quadratic lattice,” Physica 27, 1209–1225 (1961).

    Article  MATH  Google Scholar 

  2. N. Elkies, G. Kuperberg, M. Larsen, and J. Propp, “Alternating sign matrices and domino tilings. Part II,” J. Algebraic Combin. 1, 219–234 (1992).

    Article  MathSciNet  MATH  Google Scholar 

  3. N. M. Bogolyubov and K. L. Malyshev, “Integrable models and combinatorics,” Russian Math. Surveys, 70, No. 5, 789–856 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  4. G. Kuperberg, “Another proof of the alternating sign matrix conjecture,” Int. Math. Res. Notices, 1996, No. 3, 139–150 (1996).

    Article  MathSciNet  MATH  Google Scholar 

  5. W. H. Mills, D. P. Robbins and H. Rumsey, “Alternating sign matrices and descending plane partitions,” J. Comb. Th. A, 34, No. 3, 340–359 (1983).

    Article  MathSciNet  MATH  Google Scholar 

  6. E. H. Lieb, “The residual entropy of square ice,” Phys. Rev., 162, 162–172 (1967).

    Article  Google Scholar 

  7. B. Sutherland, “Exact solution of a two-dimensional model for hydrogen-bonded crystals,” Phys. Rev. Lett., 19, 103–104 (1967).

    Article  Google Scholar 

  8. R. J. Baxter, “Exactly Solvable Models in Statistical Mechanics,” San Diego, CA, Academic Press, 1982.

    MATH  Google Scholar 

  9. A. G. Izergin, D. A. Coker, and V. E. Korepin, “Determinant formula for the six-vertex model,” J. Phys. A 25, 4315–4334 (1992).

    Article  MathSciNet  MATH  Google Scholar 

  10. L. Pauling, “The structure and entropy of ice and of other crystals with some randomness of atomic arrangement,” J. Amer. Chem. Soc. 57, No. 12, 2680–2684 (1935).

    Article  Google Scholar 

  11. C. Garrod, “Stochastic models of crystal growth in two dimensions,” Phys. Rev. A 41, 4184–4194 (1990).

    Article  Google Scholar 

  12. C. Garrod, A. C. Levi and M. Touzani, “Mapping of crystal growth onto the 6-vertex model,” Solid State Comm. 75, 375–382 (1990).

    Article  Google Scholar 

  13. H. Y. Huang, F. Y. Wu, H. Kunz and D. Kim, “Interacting dimers on the honeycomb lattice: an exact solution of the five-vertex model,” Physica A 228, No. 1, 1–32 (1996).

    Article  MathSciNet  Google Scholar 

  14. K. Motegi and K. Sakai, “Vertex models, TASEP and Grothendieck polynomials,” J. J. Phys. A: Math. Theor. 46, No. 35, 355201 (2013).

  15. B. Brubaker, V. Buciumas, D. Bump, and H. P. A. Gustafsson, “Colored five-vertex models and demazure atoms,” J. Combin. Theory A, 178, 105354 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  16. I. N. Burenev and A. G. Pronko, “Determinant formulae for the five-vertex model,” J. Phys. A: Math. Theor., 54, 055008 (2021).

    Article  MATH  Google Scholar 

  17. V. E. Korepin, N. M. Bogoliubov, and A. G. Izergin, Quantum Inverse Scattering Method and Correlation Functions, Cambridge University Press, Cambridge, 1993.

    Book  MATH  Google Scholar 

  18. N. M. Bogoliubov, “Four-vertex model and random tilings,” Theor. Math. Phys., 155, 523–535 (2008).

    Article  MathSciNet  MATH  Google Scholar 

  19. N. M. Bogoliubov and T. Nasar, “On the spectrum of the non-Hermitian phase-difference model,” Phys. Lett. A, 234, 345–350 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  20. I. G. Macdonald, Symmetric Functions and Hall Polynomials, 2nd edition, Oxford University Press, Oxford (1995).

    MATH  Google Scholar 

  21. I. N. Burenev and A. G. Pronko, “Quantum Hamiltonians generated by the R-matrix of the five-vertex model,” Zap. Nauchn. Semin. POMI 494, 103–124 (2020); English transl., J. Math. Sci,, 264, 271–285 (2022)..

  22. A. G. Pronko, “The five-vertex model and enumerations of plane partitions,” J. Math. Sci., 213, 756–768 (2016).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. St. Petesburg Department of Mathematics Institute, St. Petersburg, Russia

    I. N. Burenev

Authors
  1. I. N. Burenev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. N. Burenev.

Additional information

Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 509, 2021, pp. 71–88.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Burenev, I.N. Five-Vertex Model and Lozenge Tilings of a Hexagon with a Dent. J Math Sci 275, 271–282 (2023). https://doi.org/10.1007/s10958-023-06679-5

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-023-06679-5

Search

Navigation