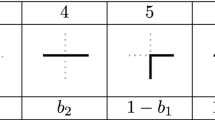
We consider the four-vertex model on a finite domain of the square lattice with the so-called scalar-product boundary conditions. It can be described in terms of nonintersecting lattice paths which are additionally restricted in their propagation in one of the two spacial directions. We compute the one-point function measuring the probability to obtain a path on a given lattice edge. We also relate this function with another one-point function which can be regarded as a local anti-ferroelectric order parameter.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
W. Li, H. Park and M. Widom, “Finite-size scaling amplitudes in a random tiling model,” J. Phys. A: Math. Gen., 23, L573–L580 (1990).
W. Li and H. Park, “Logarithmic singularity in the surface free energy near commensurate- incommensurate transitions,” J. Phys. A: Math. Gen., 24, 257–264 (1991).
N. M. Bogoliubov, “Four-vertex model and random tilings,” Theor. Math. Phys., 155, 523–535 (2008).
N. M. Bogoliubov, “Four-vertex model,” J. Math. Sci., 151, 2816–2828 (2008).
N. M. Bogolyubov and C. Malyshev, “Integrable models and combinatorics,” Russian Math. Surveys 70, 789–856 (2015).
H. Cohn, M. Larsen and J. Propp, “The shape of a typical boxed plane partition,” New York J. Math., 4, 137–165 (1998).
J. de Gier, R. Kenyon and S. S. Watson, “Limit shapes for the asymmetric five vertex model,” Commun. Math. Phys., 385, 793–836 (2021).
A. G. Pronko, “The five-vertex model and enumerations of plane partitions,” J. Math. Sci., 213, 756–768 (2016).
P. Bleher and K. Liechty, “Six-vertex model with partial domain wall boundary conditions: Ferroelectric phase,” J. Math. Phys., 56, 023302 (2015).
I. G. Macdonald, Symmetric Functions and Hall Polynomials, 2nd ed., Oxford University Press, Oxford (1995).
V. E. Korepin, N. M. Bogoliubov and A. G. Izergin, Quantum Inverse Scattering Method and Correlation Functions, Cambridge University Press, Cambridge (1993).
F. Colomo, G. Di Giulio and A. G. Pronko, “Six-vertex model on a finite lattice: integral representations for nonlocal correlation functions,” Nucl. Phys. B 972, 115535 (2021).
D. M. Bressoud, Proofs and Confirmations: the Story of the Alternating Sign Matrix Conjecture, Cambridge University Press, Cambridge (1999).
M. L. Mehta, Random Matrices, Elsevier, Amsterdam, 3rd. ed., (2004).
V. E. Korepin and P. Zinn-Justin, “Thermodynamic limit of the six-vertex model with domain wall boundary conditions,” J. Phys. A 33, 7053–7066 (2000).
O. F. Syljuasen and M. B. Zvonarev, “Monte-Carlo simulations of vertex models,” Phys. Rev. E 70, 016118 (2004).
D. Allison and N. Reshetikhin, “Numerical study of the 6-vertex model with domain wall boundary conditions,” Ann. Inst. Fourier (Grenoble) 55, 1847–1869 (2005).
V. S. Kapitonov and A. G. Pronko, “Six-vertex model as a Grassmann integral, one-point function, and the arctic ellipse,” Zap. Nauchn. Semin. POMI 494, 168–218 (2020).
P. Belov and N. Reshetikhin, “The two-point correlation function in the six-vertex model,” J. Phys. A, 55, 155001 (2022).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 509, 2021, pp. 39–53.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bogolyubov, N.M., Pronko, A.G. One-Point Function of the Four-Vertex Model. J Math Sci 275, 249–258 (2023). https://doi.org/10.1007/s10958-023-06677-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-023-06677-7